RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS

RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.1
• RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.2
• RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Ex 14.3
• RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes Revision Exercise
• RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS
• RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes MCQS

Question 1.
The radii of the bases of a cylinder and a cone are in the ratio 3 : 4 and their heights are in the ratio 2 : 3. What is the ratio of their volumes ?
Solution:
Radii of the bases of a cylinder and a cone = 3:4
and ratio in their heights = 2:3
Let r_1, r₂ be the radii and h₁ and h₂ be their heights
heights of the cylinder and cone respectively,

Question 2.
If the heights of two right circular cones are in the ratio 1 : 2 and the perimeters of their bases are in the ratio 3 : 4. What is the ratio of their volumes ?
Solution:
Ratio in the heights of two cones =1:2 and ratio in the perimeter of their bases = 3:4
Let r₁, r₂ be the radii of two cones and ht and h2 be their heights

Question 3.
If a cone and sphere have equal radii and equal volumes what is the ratio of the diameter of the sphere to the height of the cone ?
Solution:
Let r be the radius of a cone, then
radius of sphere = r
Let h be the height of cone
Now volume of cone = volume of sphere

Question 4.
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. What is the ratio of their volumes?
Solution:
Let r and h be the radius and heights of a cone, a hemisphere and a cylinder
∴ Volume of cone =  \((\frac { 1 }{ 3 } )\) πr²h
Volume of hemisphere = \((\frac { 2 }{ 3 } )\) πr³

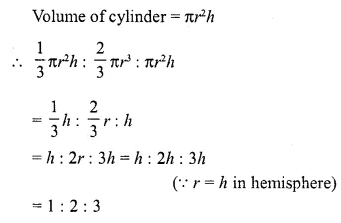
Question 5.
The radii of two cylinders are in the ratio 3 : 5 and their heights are in the ratio 2 : 3. What is the ratio of their curved surface areas ?
Solution:
Radii of two cylinders are in the ratio = 3:5
and ratio in their heights = 2:3
Let r₁, r₂ be the radii and h₁, h₂ be the heights of the two cylinders respectively, then

Question 6.
Two cubes have their volumes in the ratio 1 : 27. What is the ratio of their surface areas ?
Solution:
Ratio in the volumes of two cubes = 1 : 27
Let a₁ and a₂ be the sides of the two cubes respectively then volume of the first area = a₁³
and volume of second cube = a_2³

Question 7.
Two right circular cylinders of equal volumes have their heights in the ratio 1 : 2. What is the ratio of their radii ?
Solution:
Ratio the heights of two right circular cylinders = 1:2
Let r₁,r₂ be their radii and h₁, h₂ be their

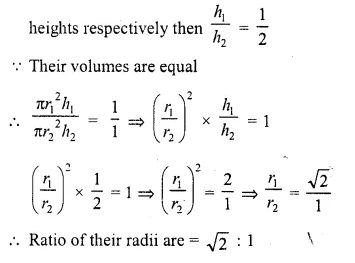
Question 8.
If the volumes of two cones are in the ratio 1 : 4, and their diameters are in the ratio 4 : 5, then write the ratio of their weights.
Solution:
Volumes of two cones are in the ratio =1:4 and their diameter are in the ratio = 4:5
Let r₁ and r₂ be the radii and h₁ ,h₂ be their

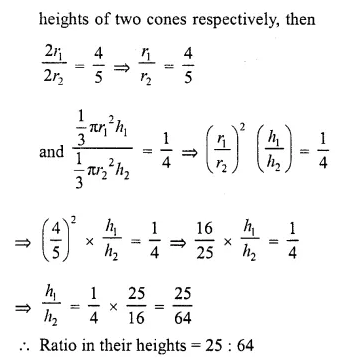
Question 9.
A sphere and a cube have equal surface areas. What is the ratio of the volume of the sphere to that of the cube ?
Solution:
Surface areas of a sphere and a cube are equal
Let r be the radius of sphere and a be the edge of cube,

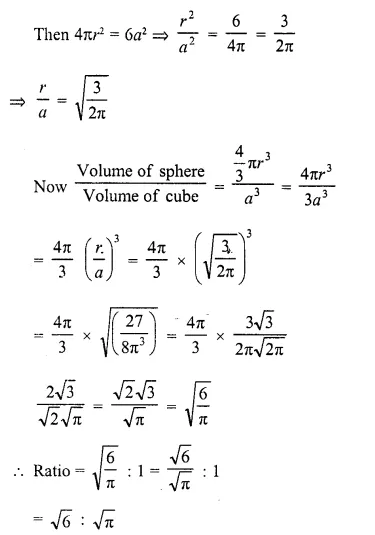
Question 10.
What is the ratio of the volume of a cube to that of a sphere which will fit inside it?
Solution:
A sphere is fit inside the cube
Side of a cube = diameter of sphere
Let a be the side of cube and r be the radius of the sphere, then

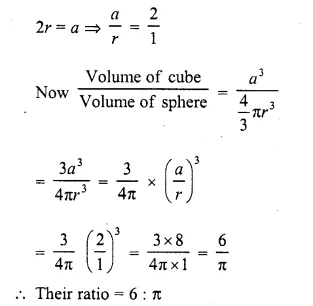
Question 11.
What is the ratio of the volumes of a cylinder, a cone and a sphere, if each has the same diameter and same height ?
Solution:
Diameters (or radii), and heights of a cylinder a cone and a sphere are equal,
Let r and h be the radius and height be the cone cylinder, cone and sphere respectively, thus their volumes will be

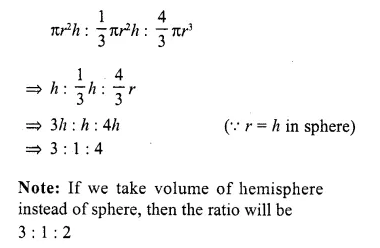
Question 12.
A sphere of maximum volume is cut-out from a solid hemisphere of radius r. What is the ratio of the volume of the hemisphere to that of the cut-out sphere?
Solution:
r is the radius of a hemisphere, then
the diameter of the sphere which is cut out of the hemisphere will be r

Question 13.
A metallic hemisphere is melted and recast in the shape of a cone with the same base radius R as that of the hemisphere. If H is the height of the cone, then write the value of \((\frac { H }{ R } )\).
Solution:
R is the radius of a hemisphere 2

Question 14.
A right circular cone and a right circular cylinder have equal base and equal height. If the radius of the base and height are in the ratio 5 : 12, write the ratio of the total surface area of the cylinder to that of the cone.
Solution:
Radius and height of a cone and a cylinder be r and h respectively

Question 15.
A cylinder, a cone and a hemisphere are of equal base and have the same height. What is the ratio of their volumes ?
Solution:
Let r and h be the radii and heights of the cylinder cone and hemisphere respectively, then
Volume of cylinder = πr²h
Volume of cone = \((\frac { 1 }{ 3 } )\) πr²h
Volume of hemisphere = \((\frac { 2 }{ 3 } )\) πr³

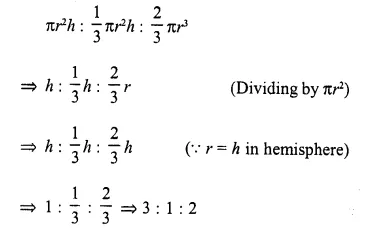
Question 16.
The radii of two cones are in the ratio 2 : 1 and their volumes are equal. What is the ratio of their heights ?
Solution:
Radii of two cones are in the ratio = 2:1
Let r₁, r₂ be the radii of two cones and h₁, h₂ be their heights respectively,

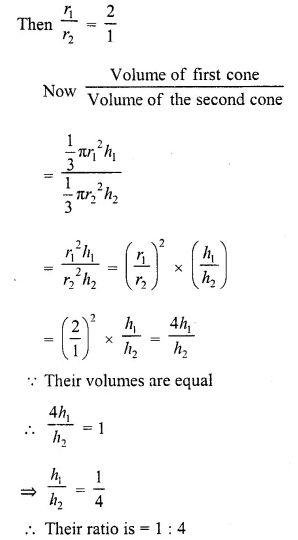
Question 17.
Two cones have their heights in the ratio 1 : 3 and radii 3:1. What is the ratio of their volumes ?
Solution:
Ratio in heights of two cones = 1:3
and ratio in their ratio = 3:1
Let r₁, r₂ be their radii and h₁, h₂ be their
heights, then

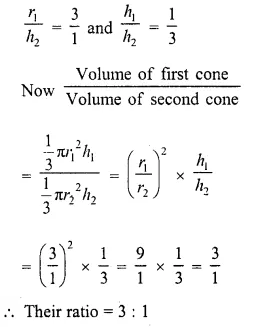
Question 18.
A hemisphere and a cone have equal bases. If their heights are also equal, then what is the ratio of their curved surfaces ?
Solution:
Bases of a hemisphere and a cone are equal
and their heights are also equal
Let r and h be their radii and heights
respectively
∴ r = h₁

Question 19.
If r₁ and r₂ denote the radii of the circular bases of the frustum of a cone such that r₁ > r₂ then write the ratio of the height of the cone of which the frustum is a part to the height of the frustum.
Solution:
r₁ , r₂ are the radii of the bases of a frustum and r₁ > r₂
Let h₁ be the height of cone and h₂ be the height of smaller cone
∴ Height of frustum = h₁ – h₂

Question 20.
If the slant height of the frustum of a cone is 6 cm and the perimeters of its circular bases are 24 cm and 12 cm respectively. What is the curved surface area of the frustum ?
Solution:
Slant height of a frustum (l) = 6 cm
Perimeter of upper base (P₁) = 24 cm
and perimeter of lower base (P₂) = 12 cm

Question 21.
If the areas of circular bases of a frustum of a cone are 4 cm² and 9 cm² respectively and the height of the frustum is 12 cm. What is the volume of the frustum ?
Solution:
In a frustum,
Area of upper base (A₁) = 4 cm²
and area of lower base (A₂) = 9 cm²

Question 22.
The surface area of a sphere is 616 cm². Find its radius.
Solution:
Surface area of a sphere = 616 cm²
Let r be the radius, then

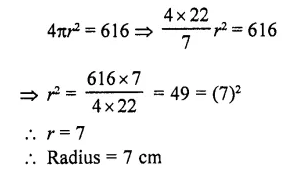
Question 23.
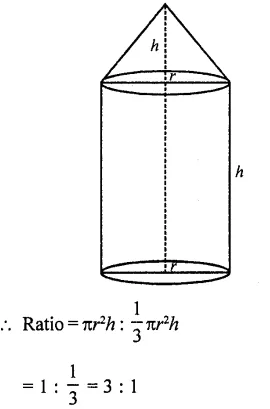
A cylinder and a cone are of the same base radius and of same height. Find the ratio of the value of the cylinder to that of the cone. [CBSE 2009]
Solution:
Let r be the radius of the base of the cylinder
small as of cone
and let height of the cylinder = h
Then height of cone = h
∴ Volume of cylinder =  πr²h
and volume of cone = \((\frac { 1 }{ 3 } )\)  πr²h

Question 24.
The slant height of the frustum of a cone is 5 cm. If the difference between the radii of its two circular ends is 4 cm, write the height of the frustum. [CBSE 2010]
Solution:
Slant height of frustum (l) = 5 cm
Difference between the upper and lower radii = 4 cm
Let h be height and upper radius r₁ and lower radius = r₂

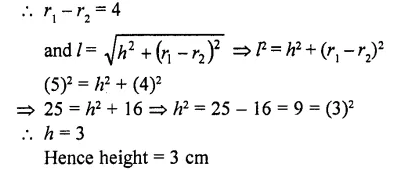
Question 25.
Volume and surface area of a solid hemisphere are numerically equal. What is the diameter of hemisphere?
Solution:
Volume of hemisphere = Surface area of hemisphere (given)

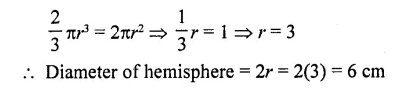
Hope given RD Sharma Class 10 Solutions Chapter 14 Surface Areas and Volumes VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.