RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3

RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3

Other Exercises

• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.1
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.2
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.4
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.5
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.6
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.7
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.8
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.9
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.10
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.11
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables VSAQS
• RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables MCQS

Solve the following systems of equations:
Question 1.
11x + 15y + 23 = 0
7x – 2y – 20 = 0
Solution:
11x + 15y + 23 = 0 => 11x + 15y = -23 ……..(i)
7x – 2y – 20 = 0 => 7x – 2y = 20 ……….(ii)
Multiply (i) by 2 and (ii) 15, we get
22x + 30y = -46
105x – 30y = 300
Adding we get
127x = 254 => x = \(\frac { 254 }{ 127 }\) = 2
7 x 2 – 2y = 20 => 14 – 2y = 20
-2y = 20 – 14 = 6
y = -3

Question 2.
3x – 7y + 10 = 0
y – 2x – 3 = 0
Solution:

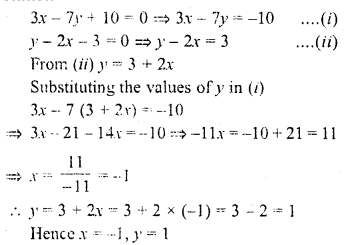
Question 3.
0.4x + 0.3y = 1.7
0.7x – 0.2y = 0.8
Solution:

Question 4.

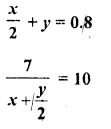
Solution:

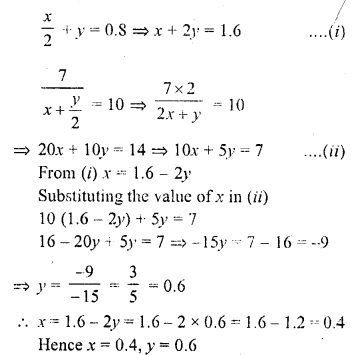
Question 5.
7(y + 3) – 2(x + 2) = 14
4(y – 2) + 3(x – 3) = 2
Solution:

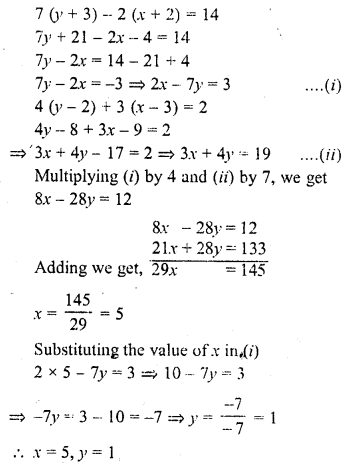
Question 6.
\(\frac { x }{ 7 } +\frac { y }{ 3 } =5\)
\(\frac { x }{ 2 } -\frac { y }{ 9 } =6\)
Solution:

Question 7.
\(\frac { x }{ 3 } +\frac { y }{ 4 } = 11\)
\(\frac { 5x }{ 6 } -\frac { y }{ 3 } = -7\)
Solution:

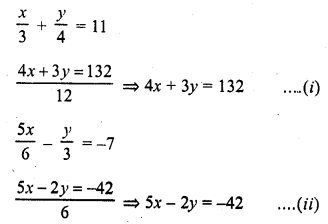
Question 8.
\(\frac { 4 }{ x }\) + 3y = 8
\(\frac { 6 }{ x }\) – 4y = -5
Solution:

Question 9.
x + \(\frac { y }{ 2 }\) = 4
\(\frac { x }{ 3 }\) + 2y = 5
Solution:

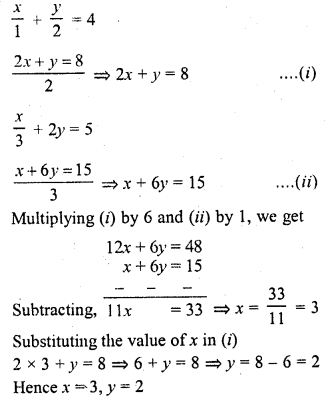
Question 10.
x + 2y = \(\frac { 3 }{ 2 }\)
2x + y = \(\frac { 3 }{ 2 }\)
Solution:

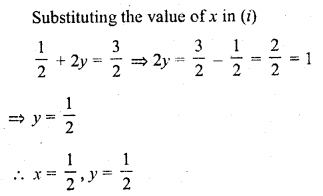
Question 11.
√2x – √3y = 0
√3x – √8y = 0
Solution:

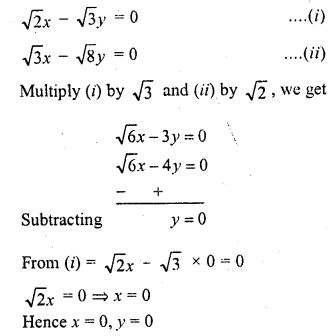
Question 12.
3x – \(\frac { y + 7 }{ 11 }\) + 2 = 10
2y + \(\frac { y + 11 }{ 7 }\) = 10
Solution:

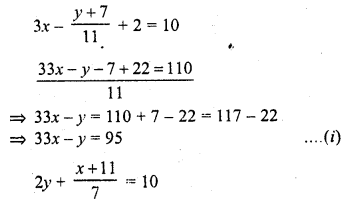
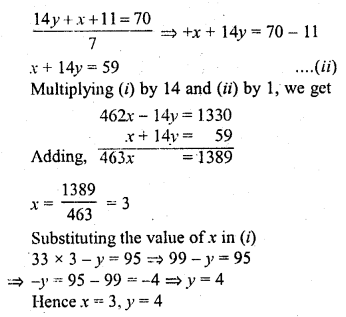
Question 13.
2x – \(\frac { 3 }{ y }\) = 9
3x + \(\frac { 7 }{ y }\) = 2, y ≠ 0
Solution:

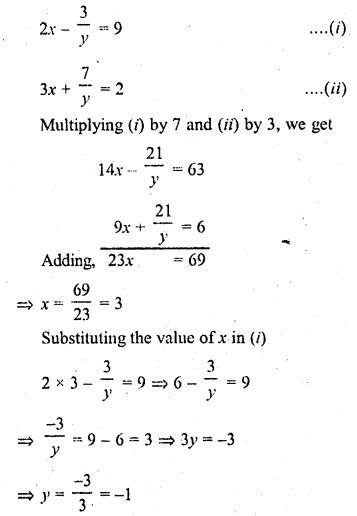
Hence x = 3, y = -1

Question 14.
0.3x + 0.7y = 0.74
0.3x + 0.5y = 0.5
Solution:

Question 15.

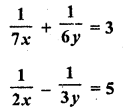
Solution:

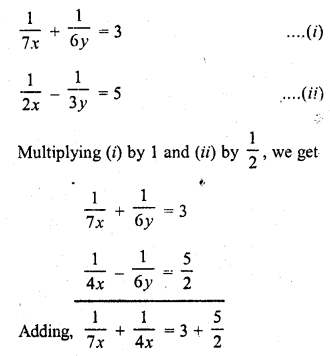
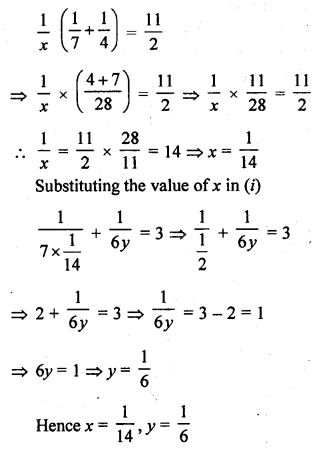
Question 16.

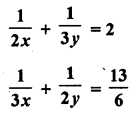
Solution:

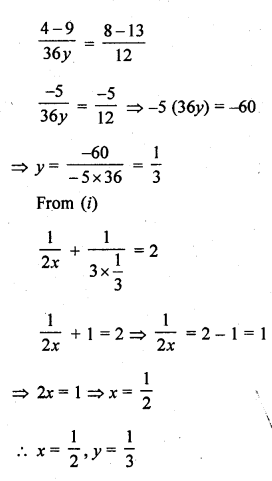
Question 17.

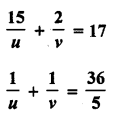
Solution:

Question 18.

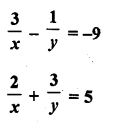
Solution:

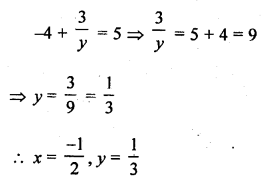
Question 19.

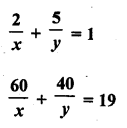
Solution:

Question 20.

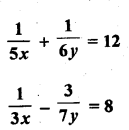
Solution:

Question 21.

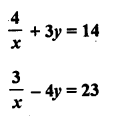
Solution:

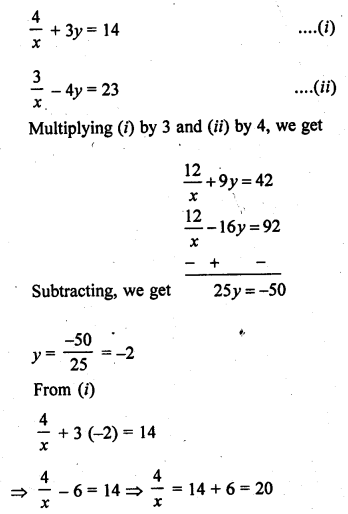
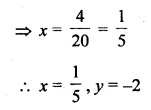
Question 22.

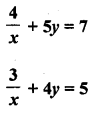
Solution:

Question 23.

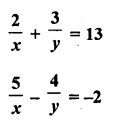
Solution:

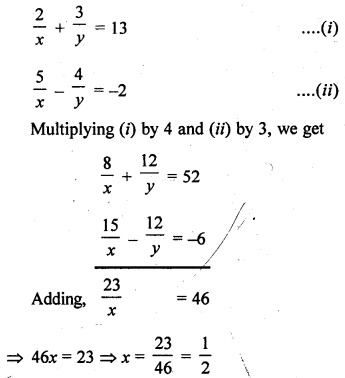
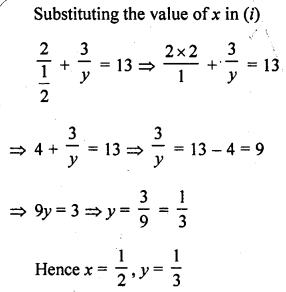
Question 24.

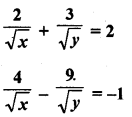
Solution:

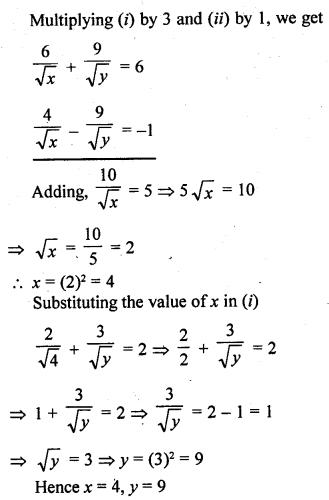
Question 25.

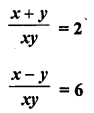
Solution:

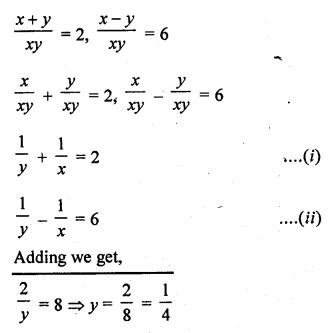
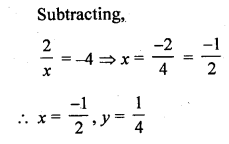
Question 26.

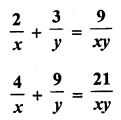
Solution:

Question 27.

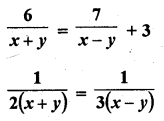
Solution:

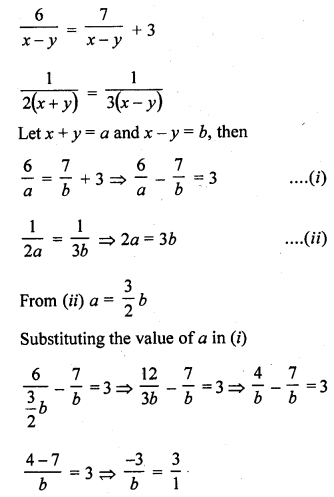
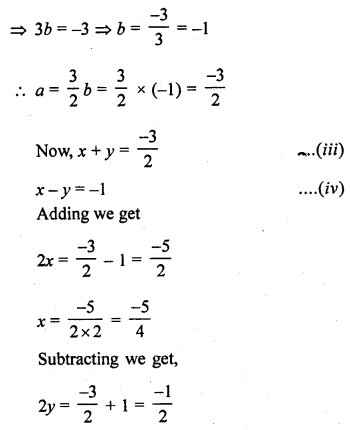
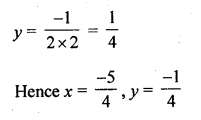
Question 28.

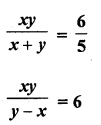
Solution:

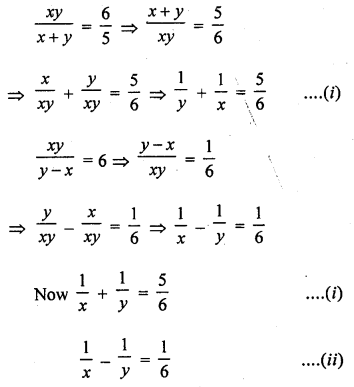
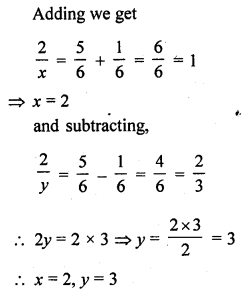
Question 29.

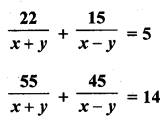
Solution:

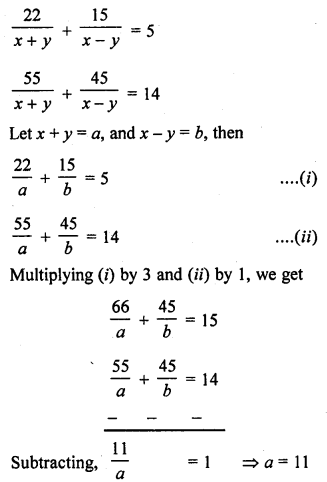
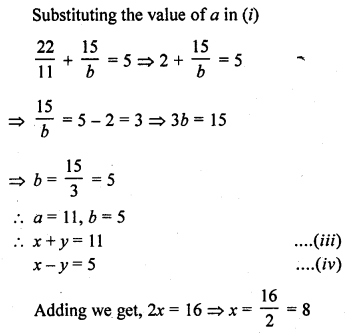
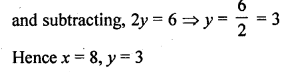
Question 30.

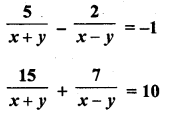
Solution:

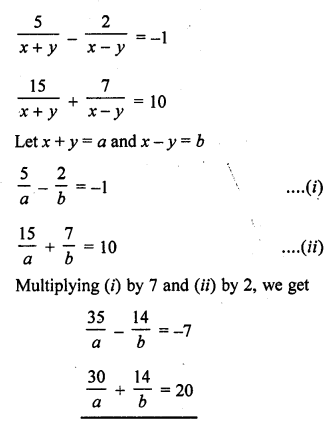
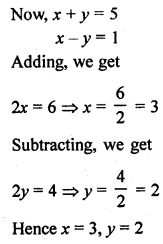
Question 31.

Solution:

Question 32.

Solution:

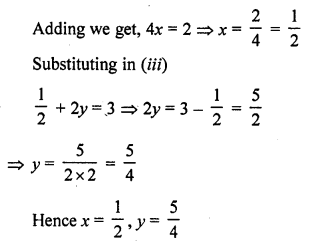
Question 33.

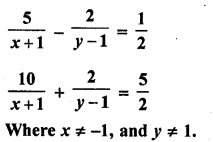
Solution:

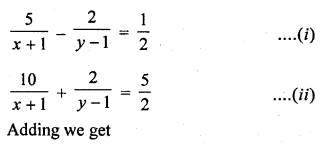
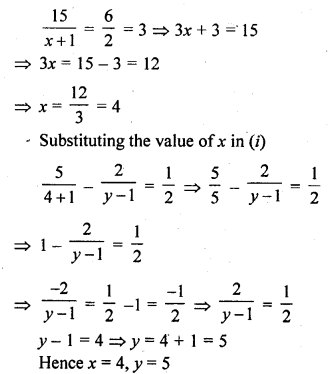
Question 34.
x + y = 5xy
3x + 2y = 13xy
Solution:

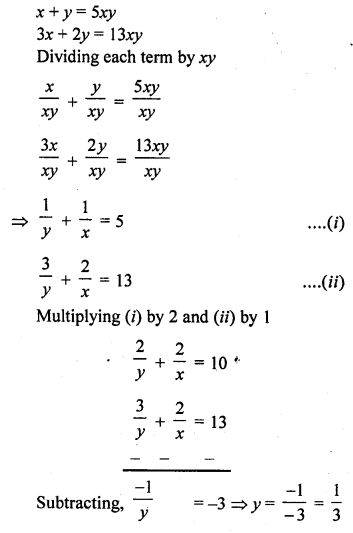
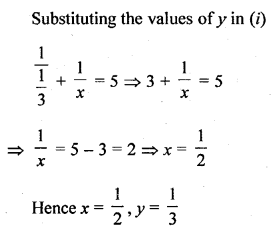
Question 35.

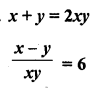
Solution:

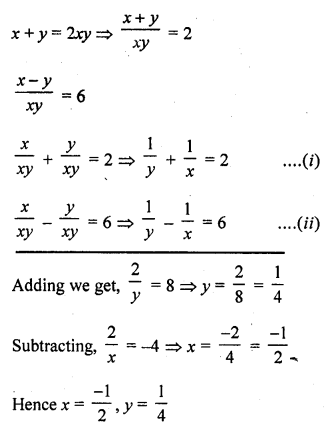
Question 36.
2 (3u – v) = 5uv
2 (u + 3v) = 5uv
Solution:

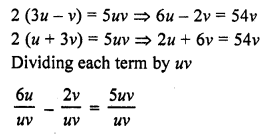
Question 37.

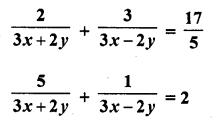
Solution:

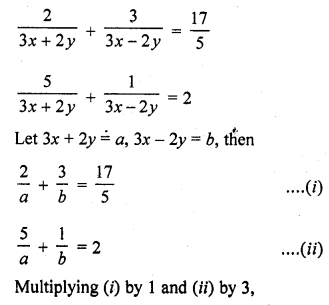
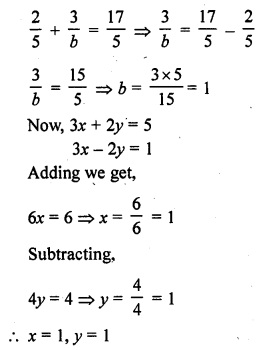
Question 38.

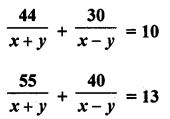
Solution:

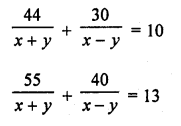
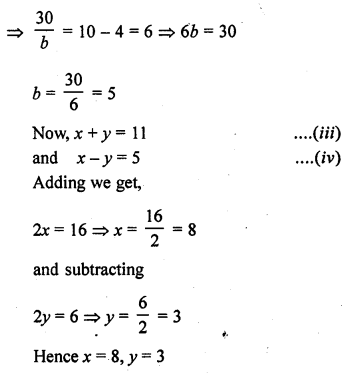
Question 39.

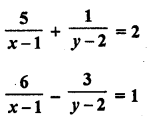
Solution:

Question 40.

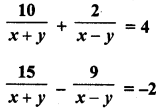
Solution:

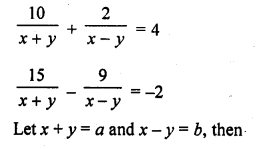
Question 41.

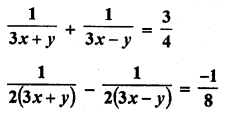
Solution:

Question 42.

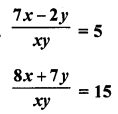
Solution:

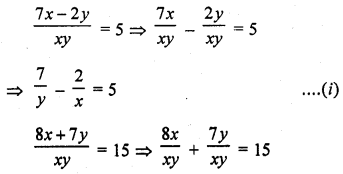
Question 43.
152x – 378y = -74
– 378x + 152y = -604
Solution:
152x – 378y = -74 ……..(i)
– 378x + 152y = -604 ………(ii)
Adding (i) and (ii), we get
– 226x – 226y = 678
Dividing by -226,
x + y = 3 ……..(iiii)
and subtracting (ii) from (i)
530x – 530y = 530
Dividing by 530,
x – y = 1 ……..(iv)
Adding (iii) and (iv)
2x = 4
x = 2
From (iii), 2 + y = 3
y = 3 – 2 = 1
Hence x = 2, y = 1

Question 44.
99x + 101y = 499
101x + 99y = 501
Solution:
99x + 101 y = 499 ….(i)
101x + 99y = 501 ……(ii)
Adding we get
200x + 200y = 1000
x + y = 5 ……(iii)
(Dividing by 200)
Subtracting we get
-2x + 2y = -2
=> x – y = 1 ….(iv)
(Dividing by -2)
Now adding (iii) and (iv)
2x = 6 => x = 3
and subtracting (iv) from (iii)
2y = 4 => y = 2
Hence x = 3, y = 2

Question 45.
23x – 29y = 98
29x – 23y = 110
Solution:
23x – 29y = 98 ….(i)
29x – 23y = 110 ….(ii)
Adding (i) and (ii) we get
52x – 52y = 208
x – y = 4 ….(iii)
(Dividing by 52)
Subtracting (ii) from (i)
6x + 6y = 12
=> x + y = 2 ….(iv)
(Dividing by 6)
Adding (iii) and (iv)
2x = 6 => x = 3
Subtracting (iv) from (iii)
2y = -2 => y = -1
Hence x = 3, y = -1

Question 46.
x – y + z = 4
x – 2y – 2z = 9
2x + y + 3z = 1
Solution:
x – y + z = 4 ……(i)
x – 2y – 2z = 9 ……(ii)
2x + y + 3z = 1 ……(iii)

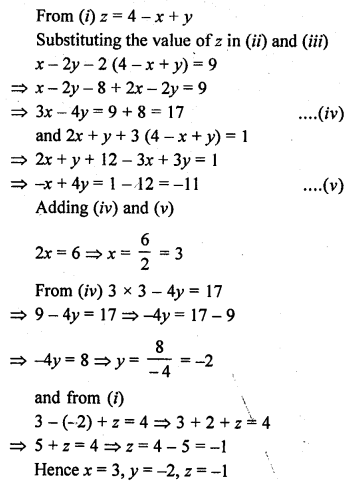
Question 47.
x – y + z = 4
x + y + z = 2
2x + y – 3z = 0
Solution:
x – y + z = 4 ….(i)
x + y + z = 2 ….(ii)
2x + y – 3z = 0 ….(iii)
From (i)
z = 4 – x + y
Substituting the values of z in (ii) and (iii)
x + y + 4 – x + y = 2
2y = 2 – 4 = -2
y = -1
and 2x + y – 3(4 – x + y) = O
2x + y – 12 + 3x – 3y = 0
5x – 2y = 12
5x – 2(-1) = 12
5x + 2 = 12
5x = 12 – 2 = 10
x = 2
From (i),
2 – (-1) + z = 4
2 + 1 + z = 4
3 + z = 4
z = 4 – 3 = 1
Hence x = 2, y = 1, z = 1

Question 48.
21x + 47y = 110
47x + 21y = 162
Solution:
We have,
21x + 47y = 110 …(i)
47x + 21y = 162 …(ii)
Multiplying equation (i) by 47 and Equation (ii) by 21, we get
987x + 2209y = 5170 …(iii)
987x + 441y = 3402 …(iv)
Subtracting equation (iv) from equation (iii),
we get
1768y = 1768
y = 1
Substituting value of y in equation (i), we get
21x + 47 = 110
or 21x = 63
or x = 3
So, x = 3, y = 1

Question 49.
If x + 1 is a factor of 2x³ + ax² + 2bx + 1, then find the values of a and b given that 2a – 3b = 4
Solution:

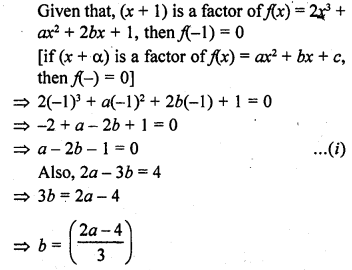
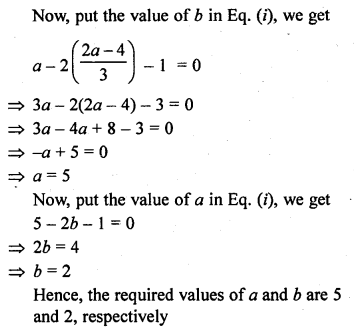
Question 50.

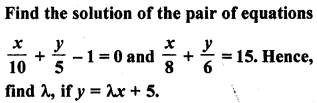
Solution:

Question 51.
Find the values of x and y in the following rectangle

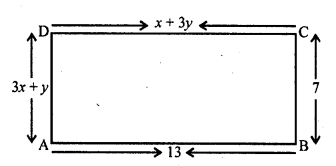
Solution:

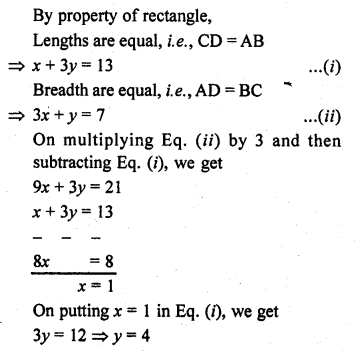
Hence, the required values of x and y are 1 and 4, respectively.

Question 52.
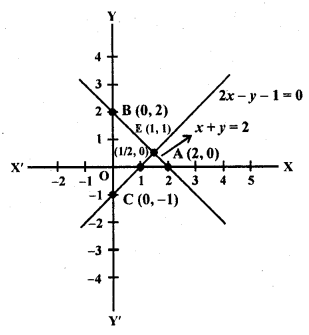
Write an equation of a line passing through the point representing solution of the pair of linear equations x + y = 2 and 2x – y = 1. How many such lines can we find?
Solution:


Plotting the points A (2, 0) and B (0, 2), we get the straight line AB. Plotting the points C (0, -1) and D (\(\frac { 1 }{ 2 }\) , 0) we get the straight line CD. The lines AB and CD intersect at E (1, 1).
Hence, infinite lines can pass through the intersection point of linear equations x + y = 2 and 2x – y = 1
¡.e.,E(1, 1) like as y = x, 2x + y = 3, x + 2y = 3, so on.

Question 53.
Write a pair of linear equations which has the unique solution x = -1, y = 3. How many such pairs can you write?
Solution:

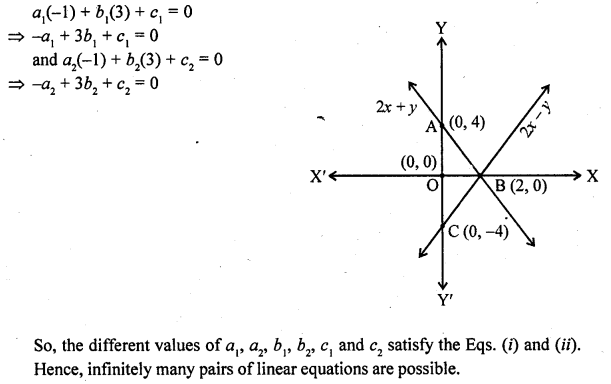
Hope given RD Sharma Class 10 Solutions Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.