RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions VSAQS

RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions VSAQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions VSAQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.1
• RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.2
• RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.3
• RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.4
• RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.5
• RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions Ex 5.6
• RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions VSAQS
• RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions MCQS

Answer each of the following questions either in one word or one sentence or as per requirement of the questions :
Question 1.
Define an arithmetic progression.
Solution:
A sequence a₁, a₂, a₃, …, an is called an arithmetic progression of then exists a constant d
Such that a₂ – a₁ = d, a₃ – a₂ = d, ………… a_n – a_n-1 = d
and so on and d is called common difference

Question 2.
Write the common difference of an A.P. whose nth term is a_n = 3n + 7.
Solution:
a_n = 3n + 7
a₁ = 3 x 1 + 7 = 3 + 7 = 10
a₂ = 3 x 2 + 7 = 6 + 7 = 13
a₃ = 3 x 3 + 7 = 9 + 7 = 16
d = a₃ – a₂ or a₂ – a₁ = 16 – 13 = 3 or 13 – 10 = 3

Question 3.
Which term of the sequence 114, 109, 104, … is the first negative term ?
Solution:
Sequence is 114, 109, 104, …..
Let a_n term be negative

Question 4.
Write the value of a₃₀ – a₁₀ for the A.P. 4, 9, 14, 19, …………
Solution:

Question 5.
Write 5th term from the end of the A.P. 3, 5, 7, 9,…, 201.
Solution:

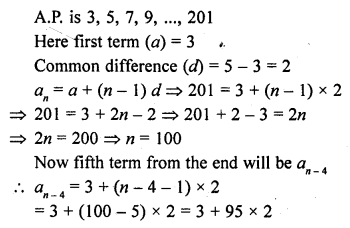
= 3 + 190 = 193
5th term from the end = 193

Question 6.
Write the value of x for which 2x, x + 10 and 3x + 2 are in A.P.
Solution:

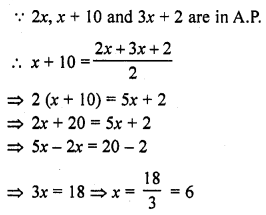
Question 7.
Write the nth term of an A.P. the sum of whose n terms is S_n.
Solution:
Sum of n terms = S_n
Let a be the first term and d be the common difference a_n =S_n – S_n-1

Question 8.
Write the sum of first n odd natural numbers.
Solution:

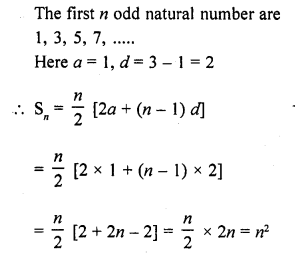
Question 9.
Write the sum of first n even natural numbers.
Solution:
First n even natural numbers are
2, 4, 6, 8, ……….
Here a = 2, d = 2

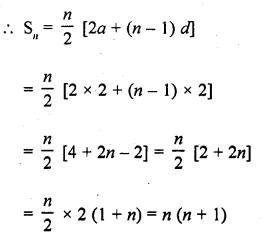
Question 10.
If the sum of n terms of an A.P. is S_n = 3n² + 5n. Write its common difference.
Solution:

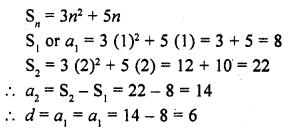
Question 11.
Write the expression for the common difference of an A.P. Whose first term is a and nth term is b.
Solution:
First term of an A.P. = a
and a_n = a + (n – 1) d = b .
Subtracting, b – a = (n – 1) d
d = \(\frac { b – a }{ n – 1 }\)

Question 12.
The first term of an A.P. is p and its common difference is q. Find its 10th term. [CBSE 2008]
Solution:
First term of an A.P. (a) = p
and common difference (d) = q
a₁₀ = a + (n – 1) d
= p + (10 – 1) q = p + 9q

Question 13.
For what value of p are 2p + 1, 13, 5p – 3 are three consecutive terms of an A.P.? [CBSE 2009]
Solution:

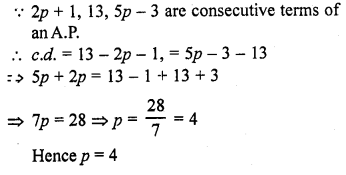
Question 14.
If \(\frac { 4 }{ 5 }\), a, 2 are three consecutive terms of an A.P., then find the value of a.
Solution:

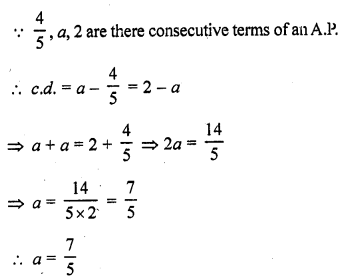
Question 15.
If the sum of first p term of an A.P. is ap² + bp, find its common difference.
Solution:

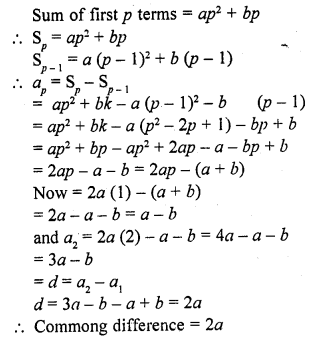
Question 16.
Find the 9th term from the end of the A.P. 5, 9, 13, …, 185. [CBSE 2016]
Solution:
Here first term, a = 5
Common difference, d = 9 – 5 = 4
Last term, l = 185
nth term from the end = l – (n – 1) d
9th term from the end = 185 – (9 – 1) 4 = 185 – 8 x 4 = 185 – 32 = 153

Question 17.
For what value of k will the consecutive terms 2k + 1, 3k + 3 and 5k – 1 form on A.P.? [CBSE 2016]
Solution:
(3k + 3) – (2k + 1) = (5k – 1) – (3k + 3)
3k + 3 – 2k – 1 = 5k – 1 – 3k – 3
k + 2 = 2k – 4
2k – k = 2 + 4
k = 6

Question 18.
Write the nth term of the A.P.
\(\frac { 1 }{ m }\) , \(\frac { 1 + m }{ m }\) , \(\frac { 1 + 2m }{ m }\) , ……… [CBSE 2017]
Solution:

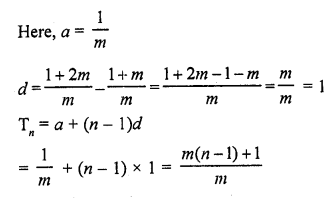
Hope given RD Sharma Class 10 Solutions Chapter 5 Arithmetic Progressions VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.