RD Sharma Class 10 Solutions Chapter 8 Circles MCQS

RD Sharma Class 10 Solutions Chapter 8 Circles MCQS

These Solutions are part of RD Sharma Class 10 Solutions. Here we have given RD Sharma Class 10 Solutions Chapter 8 Circles MCQS

Other Exercises

• RD Sharma Class 10 Solutions Chapter 8 Circles Ex 8.1
• RD Sharma Class 10 Solutions Chapter 8 Circles Ex 8.2
• RD Sharma Class 10 Solutions Chapter 8 Circles VSAQS
• RD Sharma Class 10 Solutions Chapter 8 Circles MCQS

Mark the correct alternative in each of the following :
Question 1.
A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q such that OQ = 12 cm. Length PQ is
(a) 12 cm
(b) 13 cm
(c) 8.5 cm
(d) √119 cm
Solution:
(d) Radius of a circle OP = 5 cm OQ = 12 cm, PQ is tangent

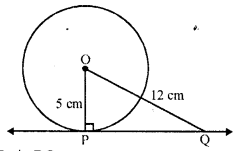
OP ⊥ PQ
In right ∆OPQ,
OQ² = OP² + PQ² (Pythagoras Theorem)
=> (12)² = (5)2 + PQ²
=> 144 = 25 + PQ²
PQ² = 144 – 25 = 119
PQ = √119

Question 2.
From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is
(a) 7 cm
(b) 12 cm
(c) 15 cm
(d) 24.5 cm
Solution:
(a) Let PQ be the tangent from Q to the circle with O as centre
PQ = 24 cm
OQ = 25 cm

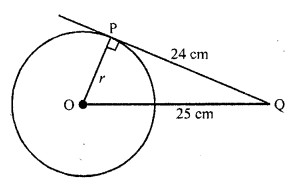
Let Radius OQ = r
OQ ⊥ PQ
Now in right ∆OPQ,
OQ² = OP² + PQ² (Pythagoras Theorem)
=> (25)² = r² + (24)²
=> 625 = r² + 576
=> r² = 625 – 576 = 49 = (7)²
r = 7
Radius of the circle = 7 cm

Question 3.
The length of the tangent from a point A at a circle, of radius 3 cm, is 4 cm. The distance of A from the centre of the circle is
(a) √7 cm
(b) 7 cm
(c) 5 cm
(d) 25 cm
Solution:
(c) Let AB be the tangent from A to the circle of centre O, then
OB = 3 cm
BA = 4 cm

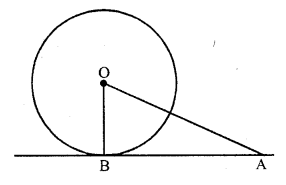
OB ⊥ BA
In right ∆OBA,
OA² = OB² + BA² (Pythagoras Theorem) = (3)² + (4)² = 9 + 16 = 25 = (5)²
OA = 5
Distance of A from the centre O = 5 cm

Question 4.
If tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of 80° then ∠POA is equal to
(a) 50°
(b) 60°
(c) 70°
(d) 80°
Solution:
(a) PA and PB are the tangents to the circle from P and ∠APB = 80°

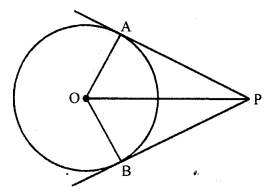
∠AOB = 180° – ∠APB = 180°- 80° = 100°
But OP is the bisector of ∠AOB
∠POA = ∠POB = \(\frac { 1 }{ 2 }\) ∠AOB
=> ∠POA = \(\frac { 1 }{ 2 }\) x 100° = 50°

Question 5.
If TP and TQ are two tangents to a circle with centre O so that ∠POQ = 110°, then, ∠PTQ is equal to
(a) 60°
(b) 70°
(c) 80°
(d) 90°
Solution:
(b) TP and TQ are the tangents from T to the circle with centre O and OP, OQ are joined and ∠POQ = 110°

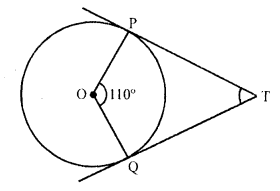
But ∠POQ + ∠PTQ = 180°
=> 110° + ∠PTQ = 180°
=> ∠PTQ = 180° – 110° = 70°

Question 6.
PQ is a tangent to a circle with centre O at the point P. If ∆OPQ is an isosceles triangle, then ∠OQP is equal to
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Solution:
(b) In a circle with centre O, PQ is a tangent to the circle at P and ∆OPQ is an isosceles triangle such that OP = PQ

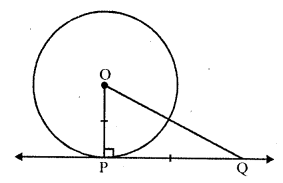
OP is radius of the circle
OP ⊥ PQ
OP = PQ
∠POQ = ∠OQP
But ∠POQ = ∠PQO = 90° (OP ⊥ PQ)
∠OQP = ∠POQ = 45°

Question 7.
Two equal circles touch each other externally at C and AB is a common tangent to the circles. Then, ∠ACB =
(a) 60°
(b) 45°
(c) 30°
(d) 90°
Solution:
(d) Two circles with centres O and O’ touch each other at C externally
A common tangent is drawn which touches the circles at A and B respectively.
Join OA, O’B and O’O which passes through C

AO = BO’ (radii of the equal circle)
AB || OO’
=> AOO’B is a rectangle
Draw another common tangent through C which intersects AB at D, then DA = DC = DB
ADCO and BDCO’ are squares
AC and BC are the diagonals of equal square
AC = BC
∠DAC = ∠DBC = 45°
∠ACB = 90°

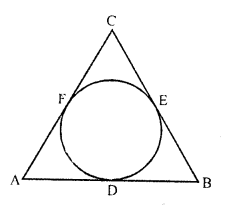
Question 8.
ABC is a right angled triangle, right angled at B such that BC = 6 cm and AB = 8 cm. A circle with centre O is inscribed in ∆ABC. The radius of the circle is
(a) 1 cm
(b) 2 cm
(c) 3 cm
(d) 4 cm
Solution:
(b) In a right ∆ABC, ∠B = 90°
BC = 6 cm, AB = 8 cm

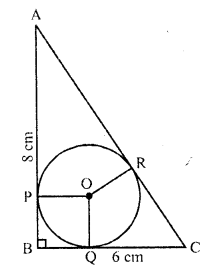
AC² = AB² + BC² (Pythagoras Theorem) = (8)² + (6)² = 64 + 36 = 100 = (10)²
AC = 10 cm
An incircle is drawn with centre 0 which touches the sides of the triangle ABC at P, Q and R
OP, OQ and OR are radii and AB, BC and CA are the tangents to the circle
OP ⊥ AB, OQ ⊥ BC and OR ⊥ CA
OPBQ is a square
Let r be the radius of the incircle
PB = BQ = r
AR = AP = 8 – r,
CQ = CR = 6 – r
AC = AR + CR
=> 10 = 8 – r + 6 – r
10 = 14 – 2r
=> 2r = 14 – 10 = 4
=> r = 2
Radius of the incircle = 2 cm

Question 9.
PQ is a tangent drawn from a point P to a circle with centre O and QOR is a diameter of the circle such that ∠POR = 120°, then ∠OPQ is
(a) 60°
(b) 45°
(c) 30°
(d) 90°
Solution:
(c) PQ is a tangent to the circle with centre O, from P, QOR is the diameter and ∠POR = 120°

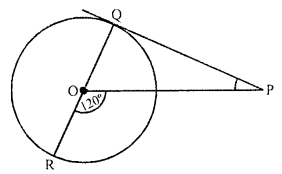
OQ is radius and PQ is tangent to the circle
OQ ⊥ QP or ∠OQP = 90°
But ∠QOP + ∠POR = 180° (Linear pair)
=> ∠QOP + 120° = 180°
∠QOP = 180° – 120° = 60°
Now in ∆POQ
∠QOP + ∠OQP + ∠OPQ = 180° (Angles of a triangle)
=> 60° + 90° + ∠OPQ = 180°
=> 150° + ∠OPQ = 180°
=> ∠OPQ = 180° – 150° = 30°

Question 10.
If four sides of a quadrilateral ABCD are tangential to a circle, then
(a) AC + AD = BD + CD
(b) AB + CD = BC + AD
(c) AB + CD = AC + BC
(d) AC + AD = BC + DB
Solution:
(b) A circle is inscribed in a quadrilateral ABCD which touches the sides AB, BC, CD and DA at P, Q, R and S respectively then the sum of two opposite sides is equal to the sum of other two opposite sides
AB + CD = BC + AD

Question 11.
The length of the tangent drawn from a point 8 cm away from the centre of a circle of radius 6 cm is
(a) √7 cm
(b) 2√7cm
(c) 10 cm
(d) 5 cm
Solution:
(b) Radius of the circle = 6 cm
and distance of the external point from the centre = 8 cm
Length of tangent = √{(8)² – (6)²}
= √(64 – 36) = √28
= √(4 x 7) = 2√7 cm

Question 12.
AB and CD are two common tangents to circles which touch each other at C. If D lies on AB such that CD = 4 cm, then AB is equal to
(a) 4 cm
(b) 6 cm
(c) 8 cm
(d) 12 cm
Solution:
(c) AB and CD are two common tangents to the two circles which touch each other externally at C and intersect AB in D

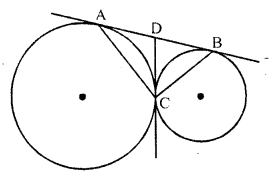
CD = 4 cm
DA and DC are tangents to the first circle from D
CD = AD = 4 cm
Similarly DC and DB are tangents to the second circle from D
CD = DB = 4 cm
AB = AD + DB = 4 + 4 = 8 cm

Question 13.
In the adjoining figure, if AD, AE and BC are tangents to the circle at D, E and F respectively. Then,

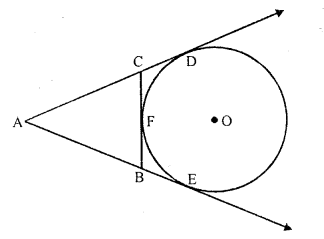
(a) AD = AB + BC + CA
(b) 2AD = AB + BC + CA
(c) 3AD = AB + BC + CA
(d) 4AD = AB + BC + CA
Solution:
(b) AD, AE and BC are the tangents to the circle at D, E and F respectively
D and AE are tangents to the circle from A
AD = AE ……(i)
Similarly, CD = CF and BE = BF ….(ii)
Now AB + AC + BC = AE – BE + AD – CD + CF + BF
= AD – BE + AD – CD + BE + BE
= 2AD [From (i) and (ii)]
or 2 AD = AB + BC + CA

Question 14.
In the figure, RQ is a tangent to the circle with centre O. If SQ = 6 cm and QR = 4 cm, then OR =

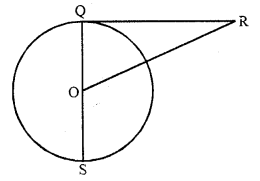
(a) 8 cm
(b) 3 cm
(c) 2.5 cm
(d) 5 cm
Solution:
(d) In the figure, 0 is the centre of the circle
QR is tangent to the circle and QOS is a diameter SQ = 6 cm, QR = 4 cm

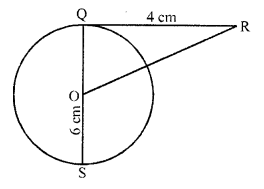
OQ = \(\frac { 1 }{ 2 }\) QS = \(\frac { 1 }{ 2 }\) x 6 = 3 cm
OQ is radius
OQ ⊥ QR
Now in right ∆OQR
OR² = QR² + QO² = (3)² + (4)² = 9 + 16 = 25 = (5)²
OR = 5 cm

Question 15.
In the figure, the perimeter of ∆ABC is
(a) 30 cm
(b) 60 cm
(c) 45 cm
(d) 15 cm

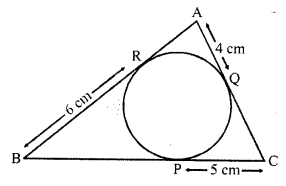
Solution:
(a) ∆ABC is circumscribed of circle with centre O
AQ = 4 cm, CP = 5 cm and BR = 6 cm
AQ and AR the tangents to the circle AQ = AR = 4 cm
Similarly BP and BR are tangents,
BP = BR = 6 cm
and CP and CQ are the tangents
CQ = CP = 5 cm

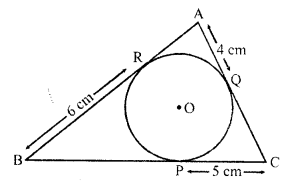
AB = AR + BR = 4 + 6 = 10 cm
BC = BP + CP = 6 + 5 = 11 cm
AC = AQ + CQ = 4 + 5 = 9 cm
Perimeter of ∆ABC = AB + BC + AC = 10 + 11 + 9 = 30 cm

Question 16.
In the figure, AP is a tangent to the circle with centre O such that OP = 4 cm and ∠OPA = 30°. Then, AP =
(a) 2√2 cm
(b) 2 cm
(c) 2√3 cm
(d) 3√2 cm

Solution:
(c) In the figure, AP is the tangent to the circle with centre O such that
OP = 4 cm, ∠OPA = 30°
Join OA, let AP = x

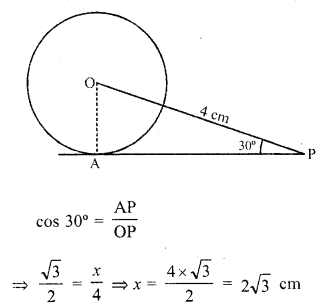
Question 17.
AP and AQ are tangents drawn from a point A to a circle with centre O and radius 9 cm. If OA = 15 cm, then AP + AQ =
(a) 12 cm
(b) 18 cm
(c) 24 cm
(d) 36 cm
Solution:
(c) OP is radius, PA is the tangent
OP ⊥ AP

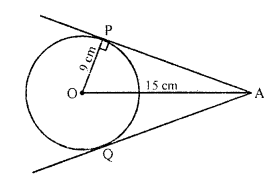
Now in right ∆OAP,
OA² = OP² + AP²
(15)² = (9)² + AP²
225 = 81 + AP²
=> AP² = 225 – 81 = 144 = (12)²
AP = 12 cm
But AP = AQ = 12 cm (tangents from A to the circle)
AP + AQ = 12+ 12 = 24 cm

Question 18.
At one end of a diameter PQ of a circle of radius 5 cm, tangent XPY is drawn to the circle. The length of chord AB parallel to XY and at a distance of 8 cm from P is
(a) 5 cm
(b) 6 cm
(c) 7 cm
(d) 8 cm
Solution:
(d) In the figure, PQ is diameter XPY is tangent to the circle with centre O and radius 5 cm
From P, at a distance of 8 cm AB is a chord drawn parallel to XY
To find the length of AB
Join OA

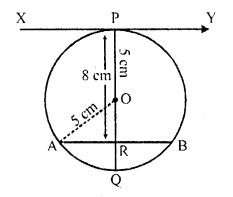
XY is tangent and OP is the radius
OP ⊥ XY or PQ ⊥ XY
AB || XY
OQ is ⊥ AB which meets AB at R
Now in right ∆OAR,
OA² = OR² + AR²
(5)² = (3)² + AR²
25 = 9 + AR²
=> AR² = 25 – 9 = 16 = (4)²
AR = 4 cm
But R is mid-point of AB
AB = 2 AR = 2 x 4 = 8 cm

Question 19.
If PT is tahgent drawn froth a point P to a circle touching it at T and O is the centre of the circle, then ∠OPT + ∠POT =
(a) 30°
(b) 60°
(c) 90°
(d) 180°
Solution:
(c) In the figure, PT is the tangent to the circle with centre O.
OP and OT are joined

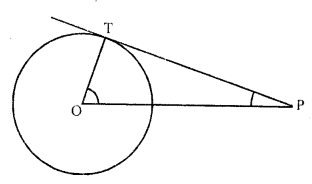
PT is tangent and OT is the radius
OT ⊥ PT
Now in right ∆OPT
∠OTP = 90°
∠OPT + ∠POT = 180° – 90° = 90°

Question 20.
In the adjacent figure, if AB = 12 cm, BC = 8 cm and AC = 10 cm, then AD =
(a) 5 cm
(b) 4 cm
(c) 6 cm
(d) 7 cm

Solution:
(d) In the figure, ∆ABC is the circumscribed a circle
AB = 12 cm, BC = 8 cm and AC = 10 cm
Let AD = a, DB = b and EC = c, then
AF = a, BE = b and FC = c

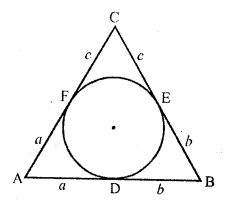
But AB + BC + AC = 12 + 8 + 10 = 30
a + b + b + c + c + a = 30
=> 2 (a + b + c) = 30
a + b + c = 15
Subtracting BC or b + c from this a = 15 – 8 = 7
AD = 7 cm

Question 21.
In the figure, if AP = PB, then
(a) AC = AB
(b) AC = BC
(c) AQ = QC
(d) AB = BC

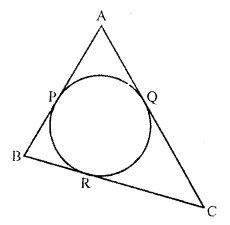
Solution:
(b) In the figure, AP = PB
But AP and AQ are the tangent from A to the circle

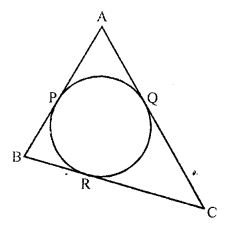
AP = AQ
Similarly PB = BR
But AP = PB (given)
AQ = BR ….(i)
But CQ and CR the tangents drawn from C to the circle
CQ = CR
Adding in (i)
AQ + CQ = BR + CR
AC = BC

Question 22.
In the figure, if AP = 10 cm, then BP =
(a) √91 cm
(b) √127 cm
(c) √119 cm
(d) √109 cm

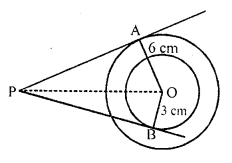
Solution:
(b) In the figure,
OA = 6 cm, OB = 3 cm and AP = 10 cm

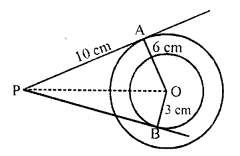
OA is radius and AP is the tangent
OA ⊥ AP
Now in right ∆OAP
OP² = AP² + OA² = (10)² + (6)² = 100 + 36 = 136
Similarly BP is tangent and OB is radius
OP² = OB² + BP²
136 = (3)² + BP2
=> 136 = 9 + BP²
=> BP² = 136 – 9 = 127
BP = √127 cm

Question 23.
In the figure, if PR is tangent to the circle at P and Q is the centre of the circle, then ∠POQ =
(a) 110°
(b) 100°
(c) 120°
(d) 90°

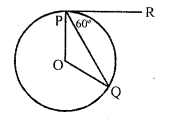
Solution:
(c) In the figure, PR is the tangent to the circle at P.
O is the centre of the circle ∠QPR = 60°

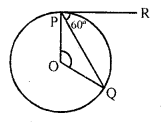
OP is the radius and PR is the tangent OPR = 90°
=> ∠OPQ + ∠QPR = 90°
=> ∠OPQ + 60° = 90°
=> ∠OPQ = 90° – 60° = 30°
OP = OQ (radii of the circle)
∠OQP = 30°
In ∆OPQ,
∠OPQ + ∠OQP + ∠POQ = 180°
=> 30° + 30° + ∠PQR = 180°
=> 60° + ∠POQ = 180°
∠POQ = 180° – 60° = 120°

Question 24.
In the figure, if quadrilateral PQRS circumscribes a circle, then PD + QB =
(a) PQ
(b) QR
(c) PR
(d) PS

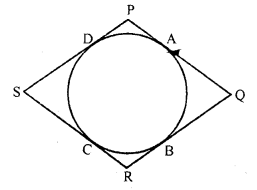
Solution:
(a) In the figure, quadrilateral PQRS is circumscribed a circle

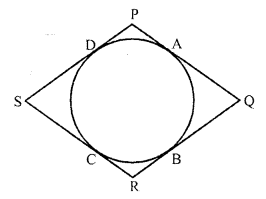
PD = PA (tangents from P to the circle)
Similarly QA = QB
PD + QB = PA + QA = PQ

Question 25.
In the figure, two equal circles touch each other at T, if QP = 4.5 cm, then QR =
(a) 9 cm
(b) 18 cm
(c) 15 cm
(d) 13.5 cm

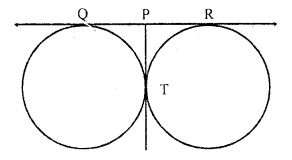
Solution:
(a) In the figure, two equal circles touch, each other externally at T
QR is the common tangent
QP = 4.5 cm

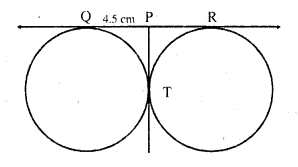
PQ = PT (tangents from P to the circle)
Similarly PT = PR
PQ = PT = PR
Now QR = PQ + PR = 4.5 + 4.5 = 9 cm

Question 26.
In the figure, APB is a tangent to a circle with centre O at point P. If ∠QPB = 50°, then the measure of ∠POQ is
(a) 100°
(b) 120°
(c) 140°
(d) 150°

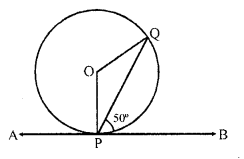
Solution:
(a) In the figure, APB is a tangent to the circle with centre O

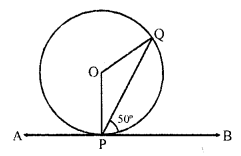
∠QPB = 50°
OP is radius and APB is a tangent
OP ⊥ AB
=> ∠OPB = 90°
=> ∠OPQ + ∠QPB = 90°
∠OPQ + 50° = 90°
=> ∠OPQ = 90° – 50° = 40°
But OP = OQ
∠OPQ = OQP = 40°
∠POQ = 180°- (40° + 40°) = 180° – 80° = 100°

Question 27.
In the figure, if tangents PA and PB are drawn to a circle such that ∠APB = 30° and chord AC is drawn parallel to the tangent PB, then ∠ABC =
(a) 60°
(b) 90°
(c) 30°
(d) None of these

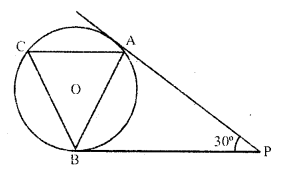
Solution:
(c) In the figure, PA and PB are the tangents to the circle with centre O

∠APB = 30°
Chord AC || BP,
AB is joined
PA = PB
∠PAB = ∠PBA
But ∠PAB + ∠PBA = 180° – 30° = 150°
=> ∠BPA + ∠PBA = 150°
=> 2 ∠PBA = 150°
=> ∠PBA = 75°
AC || BC
∠BAC = ∠PBA = 75°
But ∠PBA = ∠ACB = 75° (Angles in the alternate segment)
∠ABC = 180° – (75° + 75°) = 180° – 150° = 30°

Question 28.
In the figure, PR =
(a) 20 cm
(b) 26 cm
(c) 24 cm
(d) 28 cm

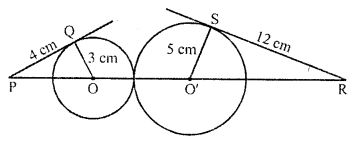
Solution:
(b) In the figure, two circles with centre O and O’ touch each other externally
PQ and RS are the tangents drawn to the circles

OQ and O’S are the radii of these circles and
OQ = 3 cm, PQ = 4 cm O’S = 5 cm and SR = 12 cm
Now in right ∆OQP
OP² = (OQ)² + PQ² = (3)² + (4)² = 9 + 16 = 25 = (5)²
OP = 5 cm
Similarly in right ∆RSO’
(O’R)² = (RS)² + (O’S)² = (12)² + (5)² = 144 + 25 = 169 = (13)²
O’R = 13 cm
Now PR = OP + OO’ + O’R = 5 + (3 + 5) + 13 = 26 cm

Question 29.
Two circles of same radii r and centres O and O’ touch each other at P as shown in figure. If OO’ is produced to meet the circle C (O’, r) at A and AT is a tangent to the circle C (O, r) such that O’Q ⊥ AT. Then AO : AO’ =
(a) \(\frac { 3 }{ 2 }\)
(b) 2
(c) 3
(d) \(\frac { 1 }{ 4 }\)

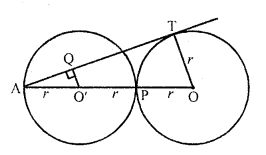
Solution:
(c) Two circles of equal radii touch each other externally at P. OO’ produced meets at A

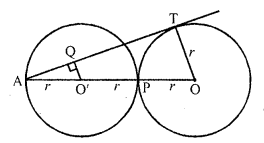
From A, AT is the tangent to the circle (O, r)
O’Q ⊥ AT
Now AO : AO’ = 3r : r
= 3 : 1 = \(\frac { 3 }{ 1 }\)

Question 30.
Two concentric circles of radii 3 cm and 5 cm are given. Then length of chord BC which touches the inner circle at P is equal to
(a) 4 cm
(b) 6 cm
(c) 8 cm
(d) 10 cm

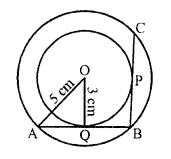
Solution:
(c) In the figure, two concentric circles of radii 3 cm and 5 cm with centre O
Chord BC touches the inner circle at P
Draw a tangent AB to the inner circle
Join OQ and OA

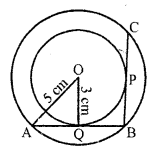
OQ is radius and AQB is the tangent
OQ ⊥ AB and OQ bisects AB
AQ = QB
Similarly, BP = PC or P is mid-point of BC
But BQ and BP are tangents from B
QB = BP = AQ
In right ∆OAQ,
OA² = AQ² + OQ²
(5)² = AQ² + (3)²
=> AQ² = (5)² – (3)²
=> AQ² = 25 – 9 = 16 = (4)²
AQ = 4 cm
BC = 2 BP = 2 BQ = 2 AQ = 2 x 4 = 8 cm

Question 31.
In the figure, there are two concentric, circles with centre O. PR and PQS are tangents to the inner circle from point plying on the outer circle. If PR = 7.5 cm, then PS is equal to
(a) 10 cm
(b) 12 cm
(c) 15 cm
(d) 18 cm

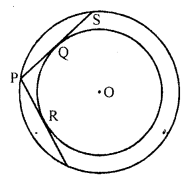
Solution:
(c) In the figure, two concentric circles with centre O
From a point P on the outer circle,
PRT and PQS are the tangents are drawn to the inner circle at R and Q respectively
PR = 7.5 cm
Join OR and OQ

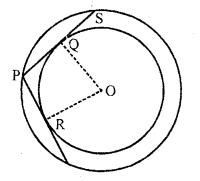
PT is chord and OR is radius
R is mid-point of PT
Similarly Q is mid-point of PS
But PR = PQ (tangents from P)
PT = 2 PR and PS = 2 PQ
PS = 2 PQ = 2 PR = 2 x 7.5 = 15 cm

Question 32.
In the figure, if AB = 8 cm and PE = 3 cm, then AE =
(a) 11 cm
(b) 7 cm
(c) 5 cm
(d) 3 cm

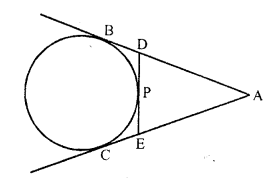
Solution:
(c) In the figure, AB and AC are the tangents to the circle from A
DE is another tangent drawn from P
AB = 8 cm, PE = 3 cm

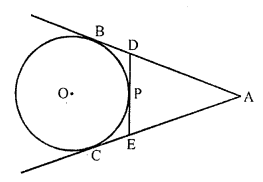
AB = AC (tangents drawn from A to the circle)
Similarly PE = EC and DP = DB
Now AE = AC – CE = AB – PE = 8 – 3 = 5 cm

Question 33.
In the figure, PQ and PR are tangents drawn from P to a circle with centre O. If ∠OPQ = 35°, then
(a) a = 30°, b = 60°
(b) a = 35°, b = 55°
(c) a = 40°, b = 50°
(d) a = 45°, b = 45°

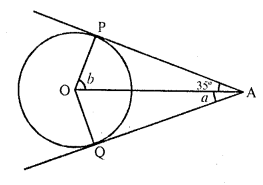
Solution:
(b) In the figure, PQ and PR are the tangents drawn from P to the circle with centre O
∠OPQ = 35°
PO is joined

PQ = PR (tangents from P to the circle)
∠OPQ = ∠OPR
=> 35° = a
=> a = 35°
OQ is radius and PQ is tangent
OQ ⊥ PQ
=> ∠OQP = 90°
In ∆OQP,
∠POQ + ∠QPO = 90°
=> b + 35° = 90°
=> b = 90° – 35° = 55°
a = 35°, b = 55°

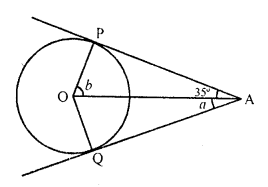
Question 34.
In the figure, if TP and TQ are tangents drawn from an external point T to a circle with centre O such that ∠TQP = 60°, then
(a) 25°
(b) 30°
(c) 40°
(d) 60°

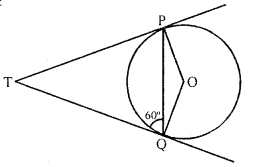
Solution:
(b) In the figure, TP and TQ are the tangents drawn from T to the circle with centre O
OP, OQ and PQ are joined
∠TQP = 60°
TP = TQ (Tangents from T to the circle)
∠TQP = ∠TPQ = 60°
∠PTQ = 180° – (60° + 60°) = 180° – 120° = 60°
and ∠POQ = 180° – ∠PTQ = 180° – 60° = 120°
But OP = OQ (radii of the same circle)
∠OPQ = ∠OQP
But ∠OPQ + ∠OQP = 180° – 120° = 60°
But ∠OPQ = 30°

Question 35.
In the figure, the sides AB, BC and CA of triangle ABC, touch a circle at P, Q and R respectively. If PA = 4 cm, BP = 3 cm and AC = 11 cm, then length of BC is [CBSE 2012]

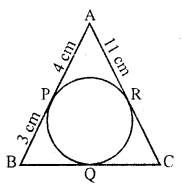
(a) 11 cm
(b) 10 cm
(c) 14 cm
(d) 15 cm
Solution:
(b) In the figure,
PA = 4 cm, BP = 3 cm, AC = 11 cm
AP and AR are the tangents from A to the circle
AP = AR
=> AR = 4 cm
Similarly BP and BQ are tangents
BQ = BP = 3 cm
AC =11 cm
AR + CR = 11 cm
4 + CR =11 cm
CR = 11 – 4 = 7 cm
CQ and CR are tangents to the circle
CQ = CR = 7 cm
Now, BC = BQ + CQ = 3 + 7 = 10 cm

Question 36.
In the figure, a circle touches the side DF of AEDF at H and touches ED and EF produced at K and M respectively. If EK = 9 cm, then the perimeter of ∆EDF is [CBSE 2012]
(a) 18 cm
(b) 13.5 cm
(c) 12 cm
(d) 9 cm

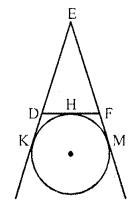
Solution:
(a) In ∆DEF
DF touches the circle at H
and circle touches ED and EF Produced at K and M respectively
EK = 9 cm
EK and EM are the tangents to the circle
EM = EK = 9 cm
Similarly DH and DK are the tangent
DH = DK and FH and FM are tangents
FH = FM
Now, perimeter of ∆DEF
= ED + DF + EF
= ED + DH + FH + EF
= ED + DK + EM + EF
= EK + EM
= 9 + 9
= 18 cm

Question 37.
In the figure DE and DF are tangents from an external point D to a circle with centre A. If DE = 5 cm and DE ⊥ DF, then the radius of the circle is [CBSE 2013]

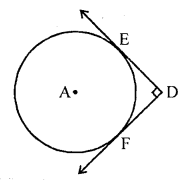
(a) 3 cm
(b) 5 cm
(c) 4 cm
(d) 6 cm
Solution:
(b) If figure, DE and DF are tangents to the circle drawn from D.
A is the centre of the circle.
DE = 5 cm and DE ⊥ DF
Join AE, AF

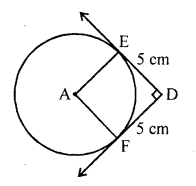
DE is the tangent and AE is radius
AE ⊥ DE
Similarly, AF ⊥ DF
But ∠D = 90° (given)
AFDE is a square
AE = DE (side of square)
But DE = 5 cm
AE = 5 cm
Radius of circle is 5 cm

Question 38.
In the figure, a circle with centre O is inscribed in a quadrilateral ABCD such that, it touches sides BC, AB, AD and CD at points P, Q, R and S respectively. If AB = 29 cm, AD = 23 cm, ∠B = 90° and DS = 5 cm, then the radius of the circle (in cm) is [CBSE 2013]

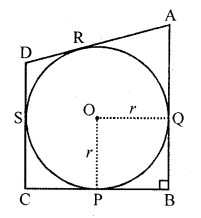
(a) 11
(b) 18
(c) 6
(d) 15
Solution:
(a) In the figure, a circle touches the sides of a quadrilateral ABCD
∠B = 90°, OP = OQ = r
AB = 29 cm, AD = 23 cm, DS = 5 cm
∠B = 90°
BA is tangent and OQ is radius
∠OQB = 90°
Similarly OP is radius and BC is tangents
∠OPB = 90°
But ∠B = 90° (given)
PBQO is a square
DS = 5 cm
But DS and DR are tangents to the circles
DR = 5 cm
But AD = 23 cm
AR = 23 – 5= 18 cm
AR = AQ (tangents to the circle from A)
AQ = 18 cm
But AB = 29 cm
BQ = 29 – 18 = 11 cm
OPBQ is a square
OQ = BQ = 11 cm
Radius of the circle = 11 cm

Question 39.
In a right triangle ABC, right angled at B, BC = 12 cm and AB = 5 cm. The radius of the circle inscribed in the triangle (in cm) is
(a) 4
(b) 3
(c) 2
(d) 1
Solution:
(c)

Question 40.
Two circles touch each other externally at P. AB is a common tangent to the circle touching them at A and B. The value of ∠APB is
(a) 30°
(b) 45°
(c) 60°
(d) 90°
Solution:
(d) We have, AT = TP and TB = TP (Lengths of the tangents from ext. point T to the circles)
∠TAP = ∠TPA = x (say)
and ∠TBP = ∠TPB = y (say)
Also, in triangle APB,
x + x + x + y + y = 180°
=> 2x + 2y = 180°
=> x + y = 90°
=> ∠APB = 90°

Question 41.
In the figure, PQ and PR are two tangents to a circle with centre O. If ∠QPR= 46, then ∠QOR equals
(a) 67°
(b) 134°
(c) 44°
(d) 46°

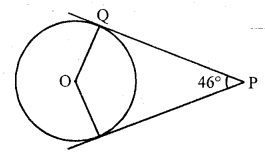
Solution:
(b) ∠OQP = 90°
[Tangent is ⊥ to the radius through the point of contact]
∠ORP = 90°
∠OQP + ∠QPR + ∠ORP + ∠QOR = 360° [Angle sum property of a quad.]
90° + 46° + 90° + ∠QOR = 360°
∠QOR = 360° – 90° – 46° – 90° = 134°

Question 42.
In the figure, QR is a common tangent to the given circles touching externally at the point T. The tangent at T meets QR at P. If PT = 3.8 cm, then the length of QR (in cm) is [CBSE2014]
(a) 3.8
(b) 7.6
(c) 5.7
(d) 1.9

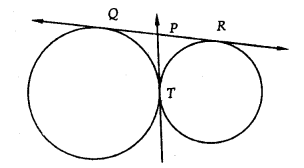
Solution:
(b) In the figure, QR is common tangent to the two circles touching each other externally at T
Tangent at T meets QR at P
PT = 3.8 cm
PT and PQ are tangents from P
PT = PQ = 3.8 cm
Similarly PT and PR are tangents
PT = PR = 3.8 cm
QR = 3.8 + 3.8 = 7.6 cm

Question 43.
In the figure, a quadrilateral ABCD is drawn to circumscribe a circle such that its sides AB, BC, CD and AD touch the circle at P, Q, R and S respectively. If AB = x cm, BC = 7 cm, CR = 3 cm and AS = 5 cm, then x =
(a) 10
(b) 9
(c) 8
(d) 7 (CBSE 2014)

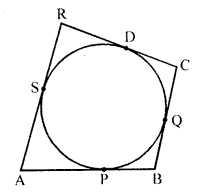
Solution:
(b) In the given figure,
ABCD is a quadrilateral circumscribe a circle and its sides AB, BC, CD and DA touch the circle at P, Q, R and S respectively
AB = x cm, BC = 7 cm, CR = 3 cm, AS = 5 cm
CR and CQ are tangents to the circle from C
CR = CQ = 3 cm
BQ = BC – CQ = 7 – 3 = 4 cm
BQ = and BP are tangents from B
BP = BQ = 4 cm
AS and AP are tangents from A
AP = AS = 5 cm
AB = AP + BP = 5 + 4 = 9 cm
x = 9 cm

Question 44.
If angle between two radii of a circle is 130°, the angle between the tangent at the ends of radii is (NCERT Exemplar)
(a) 90°
(b) 50°
(c) 70°
(d) 40°
Solution:
(b) O is the centre of the circle.
Given, ∠POQ = 130°
PT and QT are tangents drawn from external point T to the circle.

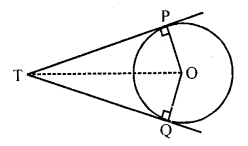
∠OPT = ∠OQT = 90° [Radius is perpendicular to the tangent at point of contact]
In quadrilateral OPTQ,
∠PTQ + ∠OPT + ∠OQT + ∠POQ = 360°
=> ∠PTQ + 90° + 90° + 130° = 360°
=> ∠PTQ = 360° – 310° = 50°
Thus, the angle between the tangents is 50°.

Question 45.
If two tangents inclined at a angle of 60° are drawn to a circle of radius 3 cm, then length of each tangent is equal to [NCERT Exemplar]
(a) \(\frac { 3\surd 3 }{ 2 }\) cm
(b) 6 cm
(c) 3 cm
(d) 3√3 cm
Solution:
(d) Let P be an external point and a pair of tangents is drawn from point P and angle between these two tangents is 60°.
Join OA and OP.

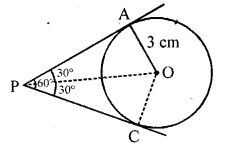
Also, OP is a bisector of line ∠APC
∠APO = ∠CPO = 30°
Also, OA ⊥ AP
Tangent at any point of a circle is perpendicular to the radius through the point of contact.

Hence, the length of each tangent is 3√3 cm

Question 46.
If radii of two concentric circles are 4 cm and 5 cm, then the length of each chord of one circle which is tangent to the other circle is [NCERT Exemplar]
(a) 3 cm
(b) 6 cm
(c) 9 cm
(d) 1 cm
Solution:
(b) Let O be the centre of two concentric circles C₁ and C₂, whose radii are r₁ = 4 cm and r₂ = 5 cm.
Now, we draw a chord AC of circle C₂, which touches the circle C₁ at B.
Also, join OB, which is perpendicular to AC. [Tangent at any point of circle is perpendicular to radius throughly the point of contact]

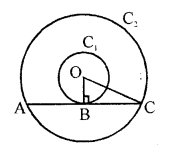
Now, in right angled ∆OBC, by using Pythagoras theorem,
OC² = BC² + BO² [(hypotenuse)² = (base)² + (perpendicular)²]
=> 5² = BC² + 4²
=> BC² = 25 – 16 = 9
=> BC = 3 cm
Length of chord AC = 2 BC = 2 x 3 = 6 cm

Question 47.
At one end A of a diameter AB of a circle of radius 5 cm, tangent XAY is drawn to the circle. The length of the chord CD parallel to XY and at a distance 8 cm from A is [NCERT Exemplar]
(a) 4 cm
(b) 5 cm
(b) 6 cm
(d) 8 cm
Solution:
(d) First, draw a circle of radius 5 cm having centre O.
A tangent XY is drawn at point A.

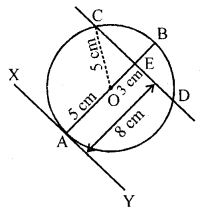
A chord CD is drawn which is parallel to XY and at a distance of 8 cm from A.
Now, ∠OAY = 90°
[Tangent and any point of a circle is perpendicular to the radius through the point of contact]
∠OAY + ∠OED = 180°
[sum of cointerior is 180°]
=> ∆OED = 180°
Also, AE = 8 cm, Join OC
Now, in right angled ∆OBC
OC² = OE² + EC²
=> EC² = OC² – OE² [by Pythagoras theorem]
EC² = 5² – 3² [OC = radius = 5 cm, OE = AE – AO = 8 – 5 = 3 cm]
EC² = 25 – 9 = 16
=> EC = 4 cm
Hence, length of chord CD = 2 CE = 2 x 4 = 8 cm
[Since, perpendicular from centre to the chord bisects the chord]

Question 48.
From a point P which is at a distance 13 cm from the centre O of a circle of radius 5 cm, the pair of tangent PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is [NCERT Exemplar]
(a) 60 cm²
(b) 65 cm²
(c) 30 cm²
(d) 32.5 cm²
Solution:
(a) Firstly, draw a circle of radius 5 cm having centre O.
P is a point at a distance of 13 cm from O.
A pair of tangents PQ and PR are drawn.
Thus, quadrilateral PQOR is formed.
OQ ⊥ QP [since, AP is a tangent line]
In right angled ∆PQO,
OP² = OQ² + QP²
=> 13² = 5² + QP²
=> QP² = 169 – 25 = 144 = 12²
=> QP = 12 cm

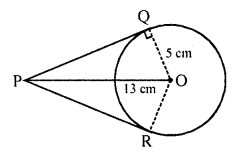
Now, area of ∆OQP = \(\frac { 1 }{ 2 }\) x QP x QO = \(\frac { 1 }{ 2 }\) x 12 x 5 = 30 cm²
Area of quadrilateral QORP = 2 ∆OQP = 2 x 30 = 60 cm²

Question 49.
If PA and PB are tangents to the circle with centre O such that ∠APB = 50°, then ∠OAB is equal to
(a) 25°
(b) 30°
(c) 40°
(d) 50°
Solution:
(a) Given, PA and PB are tangent lines.
PA = PB [Since, the length of tangents drawn from an ∠PBA = ∠PAB = θ [say]

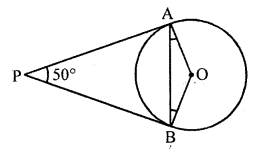
In ∆PAB,
∠P + ∠A + ∠B = 180°
[since, sum of angles of a triangle = 180°
50°+ θ + θ = 180°
2θ = 180° – 50° = 130°
θ = 65°
Also, OA ⊥ PA
[Since, tangent at any point of a circle is perpendicular to the radius through the point of contact]
∠PAO = 90°
=> ∠PAB + ∠BAO = 90°
=> 65° + ∠BAO = 90°
=> ∠BAO = 90° – 65° = 25°

Question 50.
The pair of tangents AP and AQ drawn from an external point to a circle with centre O are perpendicular to each other and length of each tangent is 5 cm. The radius of the circle is [NCERT Exemplar]
(a) 10 cm
(b) 7.5 cm
(c) 5 cm
(d) 2.5 cm
Solution:
(c)

Question 51.
In the figure, if ∠AOB = 125°, then ∠COD is equal to [NCERT Exemplar]

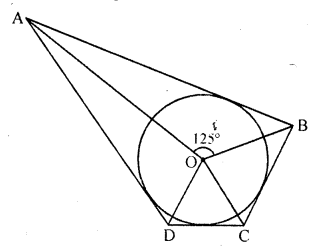
(a) 45°
(b) 35°
(c) 55°
(d) 62\(\frac { 1 }{ 2 }\)°
Solution:
(c) We know that, the opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
∠AOB + ∠COD = 180°
=> ∠COD = 180° – ∠AOB = 180° – 125° = 55°

Question 52.
In the figure, if PQR is the tangent to a circle at Q whose centre is O, AB is a chord parallel to PR and ∠BQR = 70°, then ∠AQB is equal to [NCERT Exemplar]

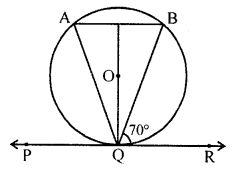
(a) 20°
(b) 40°
(c) 35°
(d) 45°
Solution:
(b) Given, AB || PR
∠ABQ = ∠BQR = 70° [alternate angles]
Also QD is perpendicular to AB and QD bisects AB.
In ∆QDA and ∆QDB
∠QDA = ∠QDB [each 90°]
AD = BD
QD = QD [common side]
∆ADQ = ∆BDQ [by SAS similarity criterion]
Then, ∠QAD = ∠QBD …(i) [c.p,c.t.]
Also, ∠ABQ = ∠BQR [alternate interior angle]
∠ABQ = 70° [∠BQR = 70°]
Hence, ∠QAB = 70° [from Eq. (i)]
Now, in ∆ABQ,
∠A + ∠B + ∠Q = 180°
=> ∠Q = 180° – (70° + 70°) = 40°

Hope given RD Sharma Class 10 Solutions Chapter 8 Circles MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.