RD Sharma Class 8 Solutions Chapter 10 Direct and Inverse variations Ex 10.2

RD Sharma Class 8 Solutions Chapter 10 Direct and Inverse variations Ex 10.2

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 10 Direct and Inverse variations Ex 10.2

Other Exercises

• RD Sharma Class 8 Solutions Chapter 10 Direct and Inverse variations Ex 10.1
• RD Sharma Class 8 Solutions Chapter 10 Direct and Inverse variations Ex 10.2

Question 1.
In which of the following tables x and y vary inversely :



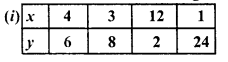
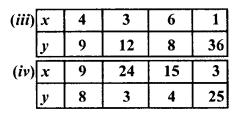
Solution:


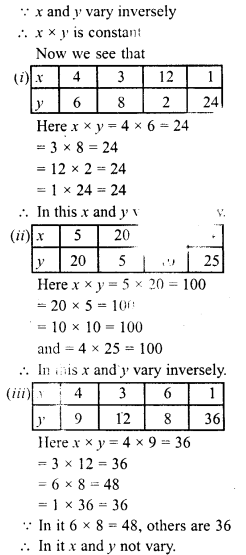
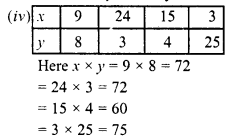
We see that it in 15 x 4 and 3 x 25 are not equal to 36 others are 72
In it x and y do not vary.

Question 2.
It x and y vary inversely, fill in the following blanks :

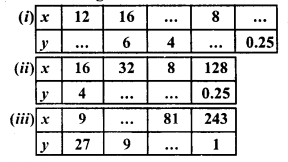
Solution:

Question 3.
Which of the following quantities vary inversely as each other ?
(i) The number of x men hired to construct a wall and the time y taken to finish the job.
(ii) The length x of a journey by bus and price y of the ticket.
(iii) Journey (x km) undertaken by a car and the petrol (y litres) consumed by it.
Solution:
(i) Here x and’y var inversely
More men less time and more time less men.
(ii) More journey more price, less journey less price
x and y do not vary inversely.
(iii) More journey more petrol, less journey, less petrol
x and y do not vary inversely.
In (i) x and y, vary inversely.

Question 4.
It is known that for a given mass of gas, the volume v varies inversely as the pressure p. Fill in the missing entries in the following table :

Solution:

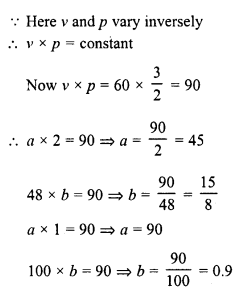
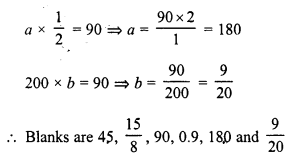
Question 5.
If 36 men can do a piece of work in 25 days, in how many days will 15 men do it ?
Solution:
Here less men, more days.
Let in x days, 15 men can finish the work
Therefore.

Question 6.
A work force of 50 men with a contractor can finish a piece of work in 5 months. In how many months the same work can be completed by 125 men.
Solution:
Let in x months, the work will be completed by 125 men

Question 7.
A work-force of 420 men with contractor can finish a certain piece of work in 9 months. How many extra men must he employ to complete the job in 7 months?
Solution:
Let total x men can finish the work in 7 months.
Therefore,


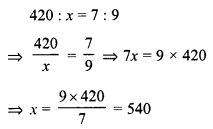
Total men = 540
Number of men already employed = 420
Extra men required = 540 – 420 = 120

Question 8.
1200 men can finish a stock of food in 35 days. How many more men should join them so that the same stock may last for 25 days ?
Solution:
Let x men can finish the stock, then

Total men required = 1680
Already men working = 1200
More men required = 1680 – 1200 = 480

Question 9.
In a hostel of 50 girls, there are food provisions for 40 days. If 30 more girls join the hostel. How long will these provisions last ?
Solution:
Number of girls in the beginning = 50
More girls joined = 30
Total number of girls = 50 + 30 = 80
Let the provisions last for x days.

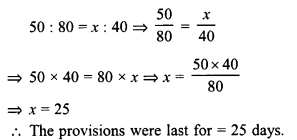
Question 10.
A car can finish a certain journey in 10 hours at the speed of 48 km/hr. By how much should its speed be increased so that it may take only 8 hours to cover the same distance ?
Solution:
Let x km/hr be the speed. Then

Speed required = 60 km/hr.
Already speed = 48 km/hr
Speed to be increase = 60 – 48 = 12 km/hr

Question 11.
1200 soldiers in a fort had enough food for 28 days. After 4 days, some soldiers were transferred to another fort and thus the food lasted now for 32 more days. How many soldiers left the fort ?
Solution:
Period = 28 days
After 4 day, the remaining period = 28 – 4 = 24 days
In the beginning number of soldiers in the fort = 1200
Period for which the food lasted = 32 days
Let for x soldier, the food was sufficient, then

Question 12.
Three spraying machines working together can finish painting a house in 60 minutes. How long will it take 5 machines of the same capacity to do the same job ?
Solution:
Let in x minutes, 5 machines can do the work
Now

Question 13.
A group of 3 friends staying together, consume 54 kg of wheat every month. Some more friends join this group and they find that the same amount of wheat lasts for 18 days. How new many numbers are there in this group now ?
Solution:
Let x members can finish the wheat in 18 day.
Therefore :


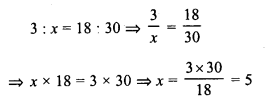
5 member can consume the wheat
Number of members already = 3
5 – 3 = 2 more member joined them.

Question 14.
55 cows can graze a field in 16 days. How many cows will graze the same field in 10 days ?
Solution:
Let number of cows required = x
Therefore :

Question 15.
18 men can reap a field in 35 days. For reaping the same field in 15 days, how many men are required ?
Solution:
Let x men are required,
Therefore,

Question 16.
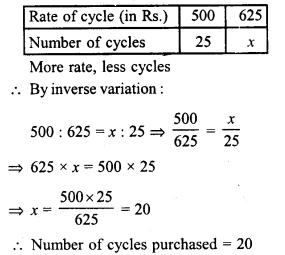
A person has money to buy 25 cycles worth Rs. 500 each. How many cycles he will be able to buy if each cycle is costing Rs. 125 more ?
Solution:
Price of one cycle = Rs. 500
Number of cycle purchased = 25
New price of the cycle = Rs. 500 + Rs. 125 = Rs. 625
Let number of cycle will be purchase = x

Question 17.
Raghu has enough money to buy 75 machines worth Rs. 200 each. How many machines can he buy if he gets a discount of Rs. 50 on each machine ?
Solution:
Price of each machine = Rs. 200
Price after given discount of Rs. 50 = Rs. 200 – 50 = Rs. 150
Let machine can be purchase = x

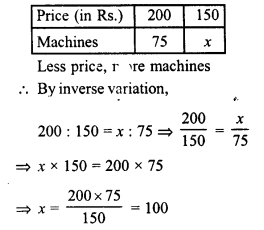
Number of machines can be purchased = 100

Question 18.
If x and y vary inversely as each other and
(i) x = 3 when y = 8, find y when x = 4
(ii) x = 5 when y = 15, find x when y = 12
(iii) x = 30, find y when constant of variation = 900.
(iv) y = 35, find x when constant of variation = 7.
Solution:
x and y vary inversely
x x y is constant of variation
(i) x = 3, y = 8
Constant = xy = 3 x 8 = 24

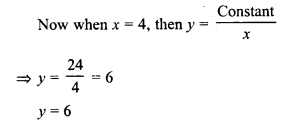
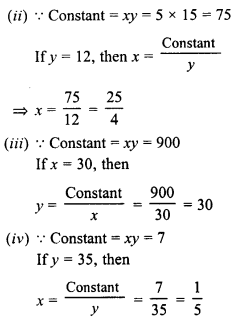
Hope given RD Sharma Class 8 Solutions Chapter 10 Direct and Inverse variations Ex 10.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.