RD Sharma Class 8 Solutions Chapter 20 Mensuration I (Area of a Trapezium and a Polygon) Ex 20.3
These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 20 Mensuration I Ex 20.3
Other Exercises
- RD Sharma Class 8 Solutions Chapter 20 Mensuration I Ex 20.1
- RD Sharma Class 8 Solutions Chapter 20 Mensuration I Ex 20.2
- RD Sharma Class 8 Solutions Chapter 20 Mensuration I Ex 20.3
Question 1.
Find the area of the pentagon shown in the figure if AD = 10 cm, AG = 8 cm, AH = 6 cm, AF = 5 cm and BF = 5 cm, CG = 7 cm and EH = 3
Solution:
In the figure, here are three triangles and one trapezium.


Question 2.
Find the area enclosed by each of the following figures as the sum of the areas of a rectangle and a trapezium:
Solution:
(i) In the figure ABCDEF,
Join CF, then, the figure consists one square and one trapezium ABCF is a square whose side = 18 cm
Area of the square = 18 x 18 cm² = 324 cm²
Area of trapezium FCDE = \(\frac { 1 }{ 2 }\) (CF + ED) x 8 cm²
= \(\frac { 1 }{ 2 }\) (18 + 7) x 8
= \(\frac { 1 }{ 2 }\) x 25 x 8 cm²
= 100 cm²
Total area of fig. ABCDEF = 324 + 100 = 424 cm²
(ii) In the figure ABCDEF,
Join BE.
The figure consists of one rectangle BCDE and one trapezium ABEF
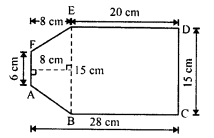
Area of rectangle BCDE = BC x CD = 20 x 15 = 300 cm²
Area of trapezium ABEF,
= \(\frac { 1 }{ 2 }\) (BE + AF) x height
= \(\frac { 1 }{ 2 }\) (15 + 6) x 8 cm²
= \(\frac { 1 }{ 2 }\) x 21 x 8 cm²
= 84 cm²
Area of the figure ABCDEF = 300 + 84 = 384 cm²
(iii) In the figure ABCDEFGH,
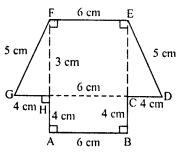
HC= AB = EF = 6 cm
AH = BC = 4 cm
DE = GF = 5 cm
Join HC.
In right ∆CDE,
ED² = CD² + CE²
⇒ (5)² = (4)² + (CE)²
⇒ 25 = 16 + (CE)²
⇒ (CE)² = 25 – 16 = 9 = (3)²
CE = 3 cm
The figure consist a rectangle and a trapezium
Area of rectangle ABCH = AB x BC = 6 x 4 = 24 cm²
Area of trapezium GDEF,
= \(\frac { 1 }{ 2 }\) (GD + EF) x CE 1
= \(\frac { 1 }{ 2 }\) (GH + HC + CD + EF) x CE
= \(\frac { 1 }{ 2 }\) (4 + 6 + 4 + 6) x 3 cm²
= \(\frac { 1 }{ 2 }\) x 20 x 3 cm²
= 30 cm²
Total area of the figure ABCDEFGH = 24 + 30 = 54 cm²
Question 3.
There is a pentagonal shaped park as shown in the figure. Jyoti and Kavita divided it in two different ways.
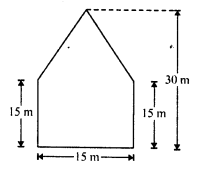
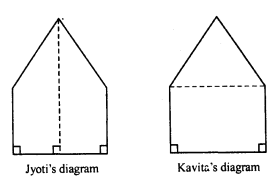
Find the area of this park using both ways. Can you suggest some another way of finding its area ?
Solution:
In first case, the figure ABCDE is divided into 2 trapezium of equal area.
Now area of trapezium DFBC
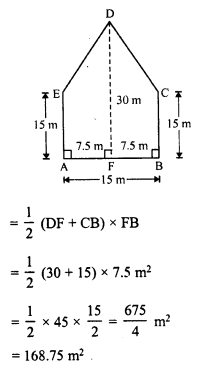
Total area of the pentagon ABCDE = 2 x 168.75 = 337.5 m²
In second case, the figure ABCDE is divided into two parts, namely one square and other triangle.
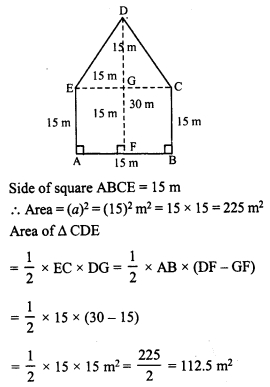
Total area of pentagon ABCDE = 225 + 112.5 = 337.5 m²
Question 4.
Find the area of the following polygon, if AL = 10 cm, AM = 20 cm, AN = 50 cm, AO = 60 cm and AD = 90 cm.
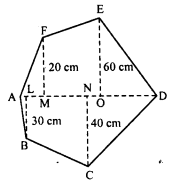
Solution:
In the figure ABCDEF,
AD = 90 cm
BL = 30 cm
AO = 60 cm
CN = 40 cm
AN = 50 cm
EO = 60 cm
AM = 20 cm
FM = 20 cm
AL = 10 cm
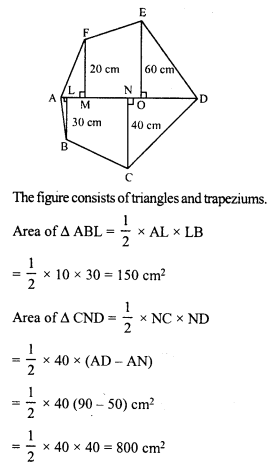


Area of ABCDEF = (150 + 800 + 900 + 200 + 1400 + 1600) cm² = 5050 cm²
Question 5.
Find the area of the following regular hexagon:
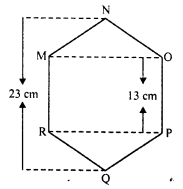
Solution:
In the regular hexagon MNOPQR There are two triangles and one rectangle.
Join MQ, MO and RP
NQ = 23 cm,
NA = BQ = \(\frac { 10 }{ 2 }\) = 5 cm
MR = OP = 13 cm
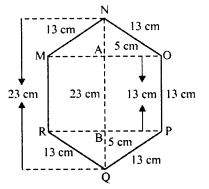
In right ∆BDQ,
PQ² = BQ² + BP²
⇒ (13)² = (5)² + BP²
⇒ 169 = 25 + BP²
⇒ BP² = 169 – 25 = 144 = (12)²
BP = 12 cm
PR = MO = 2 x 12 = 24 cm
Now area of rectangle RPOM = RP x PO = 24 x 13 = 312 cm²
Area of ∆PRQ = \(\frac { 1 }{ 2 }\) x PR x BQ
= \(\frac { 1 }{ 2 }\) x 24 x 5 = 60 cm²
Similarly area ∆MON = 60 cm²
Area of the hexagon MNOPQR = 312 + 60 + 60 = 432 cm²
Hope given RD Sharma Class 8 Solutions Chapter 20 Mensuration I Ex 20.3 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.