RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.3
These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.3
Other Exercises
- RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.1
- RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.2
- RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.3
- RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.4
Question 1.
Find the surface area of a cuboid whose :
(i) length = 10 cm, breadth = 12 cm and height = 14 cm
(ii) length = 6 dm, breadth = 8 dm, height = 10 dm
(iii) length = 2 m, breadth = 4 m and height = 5 m
(iv) length = 3.2 m, breadth = 30 dm, height = 250 cm.
Solution:
(i) Length of cuboid (l) = 10 cm
Breadth (b) = 12 cm
Height (h) = 14 cm
∴ Surface area = 2(1 × b + b × h + h × l)
= 2(10 x 12 + 12 x 14 + 14 x 10) cm2
= 2(120+ 168 + 140) cm2
= 2 x 428 = 856 cm2
(ii) Length of cuboid (l) = 6 dm
Breadth (b) = 8 dm
Height (h) = 10 dm
∴ Surface area = 2 ( l × b + b x h + h× l)
= 2(6 x 8 + 8 x 10 + 10 x 6) dm2
= 2(48 + 80 + 60) dm2 = 2 x 188 = 376 dm2
(iii) Length of cuboid (l) = 2 m
Breadth (b) = 4 m
Height (h) = 5 m
∴ Surface area = 2(l × b + b × h + h × l)
= 2(2 x 4 + 4 x 5 + 5 x 2) m2
= 2(8 + 20 + 10) m2 = 76 m2
(iv) Length of cuboid (l) = 3.2 m = 32 dm
Breadth (b) = 30 dm
Height (h) = 250 cm = 25 dm
∴ Surface area = 2(1 x b + b x h + h x l)
= 2(32 x 30 + 30 x 25 + 25 x 32) dm2
= 2(960 + 750 + 800) dm2
= 2 x 2510 = 5020 dm2
Question 2.
Find the surface area of a cube whose edge is
(i) 1.2 m
(ii) 27 cm
(iii) 3 cm
(iv) 6 m
(v) 2.1m
Solution:
(i) Edge of the cube (a) = 1.2 m
∴ Surface area = 6a2= 6 x (1,2)2 m2
= 6 x 1.44 = 8.64 m2
(ii) Edge of cube (a) = 27 cm
∴ Surface area = 6a2 = 6 x (27)2 m2
= 6 x 729 = 4374 m2
(iii) Edge of cube (a) = 3 cm
Surface area = 6a2 = 6 x (3)2 m2
= 6×9 cm2 = 54 cm2
(iv) Edge of cube (a) = 6 m
∴ Surface area = 6a2 = 6 x (6)2 m2
= 6 x 6 x 6 = 216 m2
(v) Edge of the cube (a) = 2.1 m
∴ Surface area = 6a2 = 6 x (2.1)2 m2
= 6 x 4.41 = 26.46 m2
Question 3.
A cuboidal box is 5 cm by 5 cm by 4 cm. Find its surface area.
Solution:
Length of cuboid box (l) = 5 cm
Breadth (b) = 5 cm
and height (h) = 4 cm
∴ Surface area = 2 (l x b + b x h + h x l)
= 2 (5 x 5 + 5 x 4 + 4 x 5) cm2
= 2 (25 + 20 + 20)
= 2 x 65 cm2
= 130 cm2
Question 4.
Find the surface area of a cube whose volume is :
(i) 343 m3
(ii) 216 dm3.
Solution:
(i) Volume of a cube = 343 m3
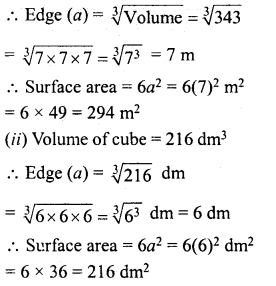
Question 5.
Find the volume of a cube whose surface area is
(i) 96 cm2
(ii) 150 m2.
Solution:
(i) Surface area of a cube = 96 cm2

Question 6.
The dimensions of a cuboid are in the ratio 5:3:1 and its total surface area is 414 m2. Find the dimensions.
Solution:
Ratio in .dimensions = 5 : 3 : 1
Let length (l) = 5x
breadth (b) = 3x
and height (h) = x
∴ Surface area = 2(1 x b + b x h + h x l)
= 2(5x x 3x + 3x x x + x x 5x)
= 2(15×2 + 3×2 + 5×2) = 2 x 23×2 = 46×2
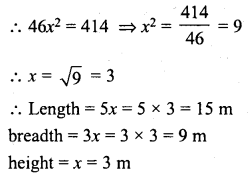
Question 7.
Find the area of the cardboard required to make a closed box of length 25 cm, 0.5 m and height 15 cm.
Solution:
Length of cardboard (l) = 25 cm
Breadth (b) = 0.5 m = 50 cm
Height (h)= 15 cm.
∴ Surface area of cardboard = 2 (l x b + b x h + h x l)
= 2(25 x 50 + 50 x 15 + 15 x 25) cm2
= 2(1250+ 750+ 375) cm2
= 2(2375)
= 4750 cm2
Question 8.
Find the surface area of a wooden box whose shape is of a cube and if the edge of the box is 12 cm.
Solution:
Edge of cubic wooden box = 12 cm
∴ Surface area = 6a2 = 6(12)2 cm2
= 6 x 144 = 864 cm2
Question 9.
The dimensions of an oil tin are 26 cm x 26 cm x 45 cm. Find the area of the tin sheet required for making 20 such tins. If 1 square metre of the tin sheet costs Rs 10, find the cost of the tin sheet used for these 20 tins.
Solution:
Length of tin (l) = 26 cm = 0.26 m
Breadth (b) = 26 cm = 0.26 m
Height (h) = 45 cm = 0.45 m
∴ Surface area = 2(l x b + b x h +h xl)
= 2(0.26 x 0.26 + 0.26 x 0.45 + 0.45 x 0.26) m2
= 2(0.0676 + 0.117 + 0.117) m2
= 2(0.3016) = 0.6032 m2
Sheet required for such 20 tins
= 0.6032 x 20= 12.064 m2
Cost of 1 m2 tin sheet = 10 m
∴ Total cost = Rs 12.064 x 10 = Rs 120.64
and area of sheet = 12.064 m2 = 120640 cm2
Question 10.
A classroom is 11 m long, 8 m wide and 5 m high. Find the sum of the areas of its floor and the four walls (including doors, windows etc.)
Solution:
Length of room (l) = 11 m
Width (b) = 8 m
and height (h) = 5 m
Area of floor = l x b = 11 x8 = 88m2
Area of four walls = 2 (l + b) x h
= 2(11 + 8) x 5 m2 = 2 x 19×5 = 190 m2
∴ Total area = 88 m2 + 190 m2 = 278 m2
Question 11.
A swimming pool is 20 m long, 15 m wide and 3 m deep. Find the cost of repairing the floor and wall at the rate of Rs 25 per square metre.
Solution:
Length of pool (l) = 20 m
Breadth (b) = 15 m
and Depth (h) = 3 m.
Area of floor = l x b = 20 x 15 = 300 m2
and area of its walls = 2(l + b) x h
= 2(20 + 15) x 3 = 2 x 35 x 3 m2 = 210 m2
∴ Total area = 300 + 210 = 510 m2
Rate of repairing it = Rs 25 per sq. metre
∴ Total cost = Rs 25 x 510 = Rs 12750
Question 12.
The perimeter of a floor of a room is 30 m and its height is 3 m. Find the area of four walls of the room.
Solution:
Perimeter of floor = 30 m
i.e. 2(1 + b) = 30 m
Height = 3 m
∴ Area of four walls = Perimeter x height = 30 x 3 = 90 m2
Question 13.
Show that the product of the areas of the floor and two adjacent walls of a cuboid is the square of its volume.
Solution:
Let length of the room = l
and breadth = b
and height = h
Volume = l x b x h
Area of floor = l x b = lb.
Area of two adjacent walls = hl x bh.
∴ Product of areas of floor and two adjacent walls of the room = lb (hi x bh)
= l2b2h2 = (l.b.h)2 = (Volume)2
Hence proved
Question 14.
The walls and ceiling of a room are to be plastered. The length, breadth and height of the room are 4.5, 3m and 350 cm, respectively. Find the cost of plastering at the rate of Rs 8 per square metre.
Solution:
Length of room (l) = 4.5 m
Width (b) = 3 m
and height (h) = 350 cm = 3.5 m
∴ Area of walls = 2(l + b) x h
= 2(4.5 + 3) x 3.5 m2 = 2 x 7.5 x 3.5 m2 = 52.5 m2
Area of ceiling = l x b = 4.5 x 3 = 13.5 m2
∴ Total area = 52.5 + 13.5 m2 = 66 m2
Rate of plastering = Rs 8 per sq. m
∴ Total cost = Rs 8 x 66 = Rs 528
Question 15.
A cuboid has total surface area of 50 m2 and lateral surface area its 30 m2. Find the area of its base.
Solution:
Total surface area of cuboid = 50 m2
Lateral surface area = 30 m2
∴ Area of floor and ceiling = 50 – 30 = 20 m2
But area of floor = area of ceiling
∴ Area of base (floor) = \(\frac { 20 }{ 2 }\) = 10 m2
Question 16.
A classroom is 7 m long, 6 m broad and 3.5 m high. Doors and windows occupy an area of 17 m2. What is the cost of white-washing the walls at the rate of Rs 1.50 per m2.
Solution:
Length of room (l) = 7 m
Breadth (b) = 6 m
and height (h) = 3.5 m
∴ Area of four walls = 2(1 + b) x h
= 2(7 + 6) x 3.5 m2 = 2 x 13 x 3.5 = 91 m2
Area of doors and windows = 17 m2
∴ Remaining area of walls = 91 – 17 = 74 m2
Rate of whitewashing = Rs 1.50 per m2
∴ Total cost = 74 x Rs 1.50 = Rs 111
Question 17.
The central hall of a school is 80 m long and 8 m high. It has 10 doors each of size 3 m x 1.5 m and 10 windows each of size 1.5 m x l m. If the cost of the white-washing the walls of the hall at the rate of Rs 1.20 per m2 is Rs 2385.60, find the breadth of the hall.
Solution:
Length of hall (l) = 80 m
Height (h) = 8 m
Size of each door = 3 m x 1.5 m
∴ Area of 10 doors = 3 x 1,5 x 10 m2
= 45 m2
A size of each windows = 1.5 m x 1 m
∴ Area of 10 windows = 1.5 m x 1 x 10= 15 m2
Total cost of whitewashing the walls = Rs 2385.60
Rate of whitewashing = Rs 1.20 per m2
∴ Area of walls which are whitewashed
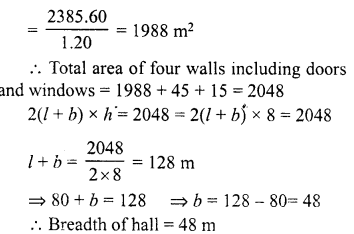
Hope given RD Sharma Class 8 Solutions Chapter 21 Mensuration II Ex 21.3 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.