RD Sharma Class 8 Solutions Chapter 22 Mensuration III Ex 22.1

RD Sharma Class 8 Solutions Chapter 22 Mensuration III (Surface Area and Volume of a Right Circular Cylinder) Ex 22.1

These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 22 Mensuration III Ex 22.1

Other Exercises

• RD Sharma Class 8 Solutions Chapter 22 Mensuration III Ex 22.1
• RD Sharma Class 8 Solutions Chapter 22 Mensuration III Ex 22.2

Question 1.
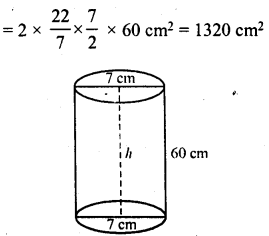
Find the curved surface area and total surface area of a cylinder, the diameter of whose base is 7 cm and height is 60 cm.
Solution:
Diameter of the base of cylinder = 7 cm
∴ Radius (r) = \(\frac { 7 }{ 2 }\) cm
Height (h) = 60m
∴ carved surface area = 2πh
= 2 x \(\frac { 22 }{ 7 }\) x \(\frac { 7 }{ 2 }\) x 60cm² = 1320cm²

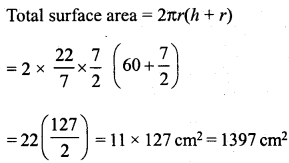
Question 2.
The curved surface area of a cylindrical road is 132 cm2. Find its length if the radius is 0.35 cm.
Solution:
Curved surface area =132 cm²
Radius (r) = 0.35 cm
Let h be the length of the rod Then 2πrh = 132

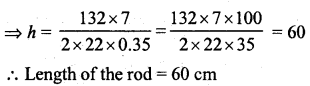
Question 3.
The area of the base of a right circular cylinder is 616 cm2 and its height is 2.5 cm. Find the curved surface area of the cylinder.
Solution:
Let r be the radius of the base of the cylinder, then
Area of the base = πr²

Question 4.
The circumference of the base of a cylinder is 88 cm and its height is 15 cm. Find its curved surface area and total surface area.
Solution:
Height of the cylinder (h) = 15 cm
Circumference of the base = 88 cm
Let r be the radius of the base, the circumference = 2πr
∴ 2πr = 88 cm …(i)

Question 5.
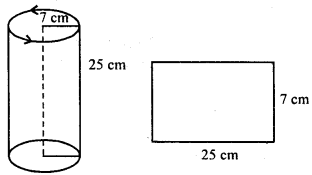
A rectangular strip 25 cm x 7 cm is rotated about the longer side. Find the total surface area of the solid thus generated.
Solution:
Dimensions of rectangular strip = 25 cm x 7 cm
By rotating the strip along longer side, a solid is formed whose radius = 7 cm
and height = 25 cm

Question 6.
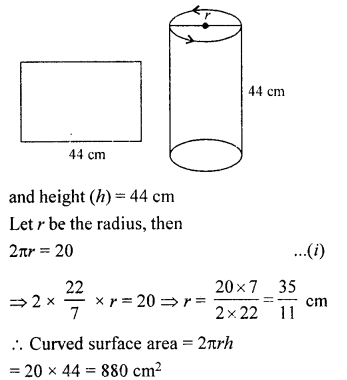
A rectangular sheet of paper 44 cm x 20 cm, is rolled along its length to form a cylinder. Find the the total surface area of the cylinder thus generated.
Solution:
By rolling along length wire, we get a cylinder whose circumference of its base = 20 cm

Question 7.
The radii of two cylinders are in the ratio of 2 : 3 and their heights are in the ratio 5 : 3. Calculate the ratio of their curved surface areas.
Solution:
Ratio in radii of two cylinders = 2:3
and ratio in their heights = 5:3

Question 8.
The ratio between the curved surface area and the total surface area of a right circular cylinder is 1: 2. Prove that its height and radius are equal.
Solution:
Let r be the radius and h be the height of a right circular cylinder, then Curved surface area = 2πrh
and total surface area = 2πrh x 2πr² = 2πr (h + r)
But their ratio is 1 : 2

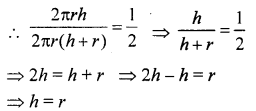
Hence their radius and height are equal.

Question 9.
The curved surface area of a cylinder is 1320 cm² and its base has diameter 21 cm. Find the height of the cylinder.
Solution:
Curved surface area of a cylinder = 1320 cm²
Diameter of its base (d) = 21 cm 21
Radius (r) = \(\frac { 21 }{ 2 }\) cm
Let h be the height of the cylinder

Question 10.
The height of a right circular, cylinder is 10.5 m. If three times the sum of the areas of its two circular faces is twice the area of the curved surface area. Find the radius of its base.
Solution:
Height of cylinder = 10.5 m
Let r be the radius and h be the height of a right circular cylinder, then Area of its two circular faces = 2π²
and area of curved surface = 2πrh
Now, according to the condition:

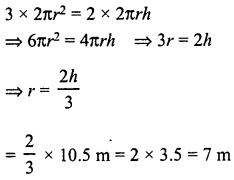
Question 11.
Find the cost of plastering the inner surface of a well at Rs 9.50 per m2, if it is 21 m deep and diameter of its top is 6 m.
Solution:
Diameter of the top of a cylindrical well = 6m

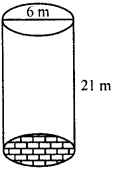
∴ Radius (r) = \(\frac { 6 }{ 2 }\) = 3 m
and depth (h) = 21 m
∴ Curved surface area = 2πrh = 2 x \(\frac { 22 }{ 7 }\) x 3 x 21 m² = 396 m²
Rate of plastering = Rs 9.50 per m²
∴ Total cost of plastering = Rs 9.50 x 396 = Rs 3,762

Question 12.
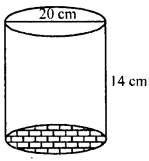
A cylindrical vessel open at the top has diameter 20 cm and height 14 cm. Find the cost of the tin-plating it on the inside at the rate of 50 paise per hundred square centimetre.
Solution:
Diameter of the vessel = 20 cm

Question 13.
The inner diameter of a circular well is 3.5 m. It is 10 m deep. Find the cost of plastering its inner curved surface at Rs 4 per square metre.
Solution:
Diameter of the well = 3.5 m

Question 14.
The diameter of a roller is 84 cm and its length is T20 cm. It takes 500 complete revolutions moving once over to level a playground. What is the area of the playground ?
Solution:
Diameter of the roller = 84 cm

Question 15.
Twenty cylindrical pillars of the Parliament House are to be cleaned. If the diameter of each pillar is 0.50 m and height is 4 m, what will be the cost of cleaning them at the rate of Rs 2.50 per square metre ?
Solution:
Diameter of each pillar = 0.50 m

Question 16.
The total surface area of a hollow cylinder which is open from both sides is 4620 sq. cm, area of the base ring is 115.5 sq. cm and height 7 cm. Find the thickness of the cylinder.
Solution:
Total surface area of a hollow cylinder opened from both sides = 4620 cm²
Area of base ring = 115.5 cm²
Height of cylinder (h) = 7 cm
Let R be the outer radius and r be the inner radius

Question 17.
The sum of the radius of the base and height of a solid cylinder is 37 m, if the total surface area of the solid cylinder is 1628 m², find the circumference of its base.
Solution:
Let r be the radius and h be the height of the solid cylinder, then r + h = 37 m …(i)
Total surface area = 1628
⇒ 2πr (r + h) = 1628

Question 18.
Find the ratio between the total surface area of a cylinder to is curved surface area,given that its height and radius are 7.5 cm and 3.5 cm.
Solution:
Radius (r) of cylinder = 3.5 cm
and height (h) = 7.5 cm
∴ Curved surface area = 2πrh
and total surface area = 2πr (h + r)
∴ Ratio = 2πr (h + r)- 2πrh = (h + r): h = 7.5 + 3.5 : 7.5
⇒ 11 : 7.5

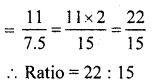
Question 19.
A cylindrical vessel, without lid, has to be tin-coated on its both sides. If the radius of the base is 70 cm and its height is 1.4 m, calculate the cost of tin-coating at the rate of Rs 3.50 per 1000 cm².
Solution:
Radius of the vessel (r) = 70 cm
and height (h) = 1.4 m = 140 cm
∴ Area of inner and outer curved surfaces and bases = 2 x 2πrh + 2πr²

 

Hope given RD Sharma Class 8 Solutions Chapter 22 Mensuration III Ex 22.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.