RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.3
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.3
Other Exercises
- RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.1
- RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.2
- RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.3
- RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.4
- RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.5
- RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials VSAQS
- RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials MCQS
In each of the following, using the remainder Theorem, find the remainder when f(x) is divided by g(x) and verify the result by actual division (1 – 8) :
Question 1.
f(x) = x3 + 4x2 – 3x + 10, g(x) = x + 4
Solution:
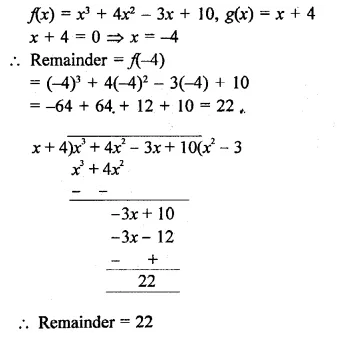
Question 2.
f(x) – 4x4 – 3x3 – 2x2 + x – 7, g(x) = x – 1
Solution:
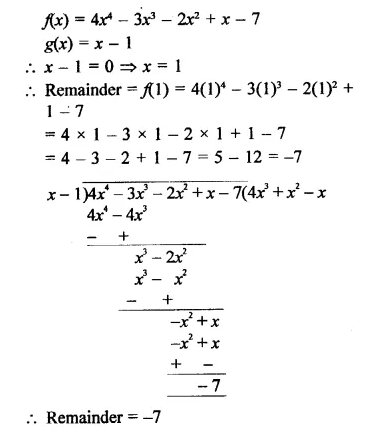
Question 3.
f(x) = 2x4 – 6X3 + 2x2 – x + 2, ,g(x) = x + 2
Solution:
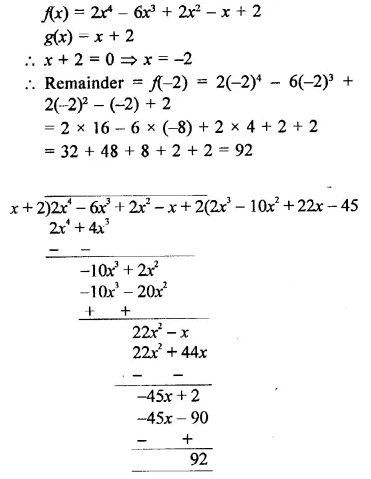
![]()
Question 4.
f(x) = 4x3 – 12x2 + 14x – 3, g(x) = 2x – 1
Solution:
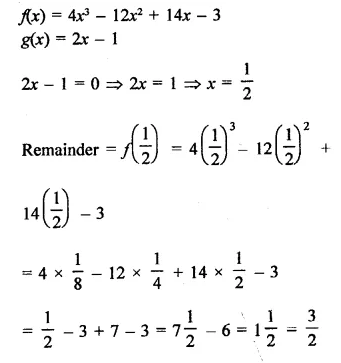
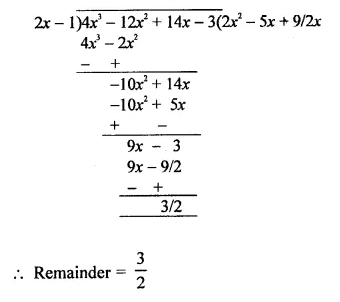
Question 5.
f(x) = x3 – 6x2 + 2x – 4, g(x) = 1 – 2x
Solution:
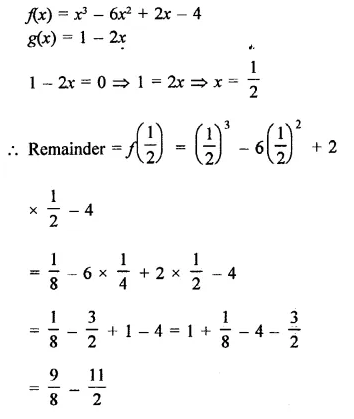
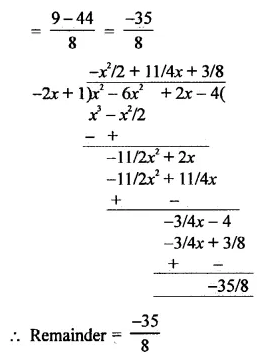
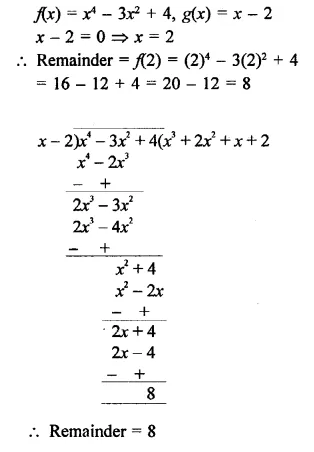
Question 6.
f(x) = x4 – 3x2 + 4, g(x) = x – 2
Solution:
Question 7.
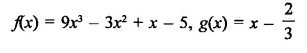
Solution:
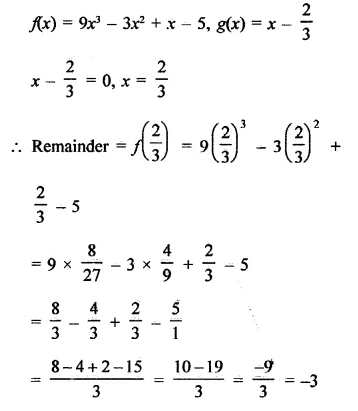
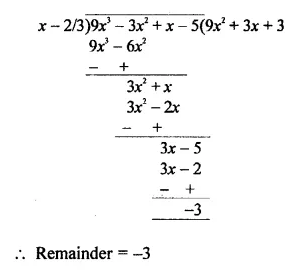
Question 8.
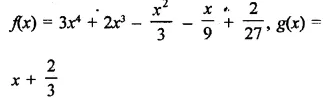
Solution:
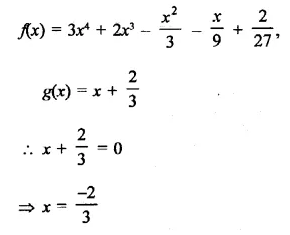
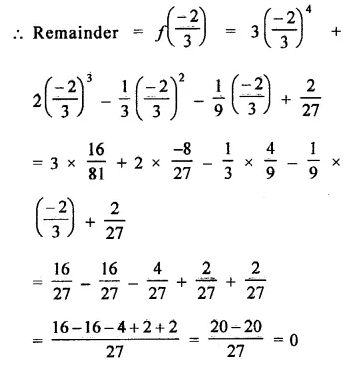
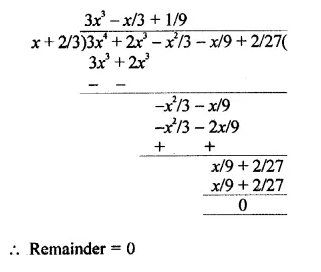
Question 9.
If the polynomials 2x3 + ax2 + 3x – 5 and x3 + x2 – 4x + a leave the same remainder when divided by x – 2, find the value of a.
Solution:
Let f(x) = 2x3 + ax2 + 3x – 5
g(x) = x3+x2-4x + a
q(x) = x – 2 ⇒ x-2 = 0 ⇒x = 2
∴ Remainder =f(2) = 2(2)3 + a(2)2 + 3 x 2-5
= 2 x 8 4-a x 4 + 3 x 2-5
= 16 + 4a + 6 – 5
= 4a +17
and g(2) = (2)3 + (2)2 -4×2 + a
= 8 + 4 – 8 + a = a + 4
∵ In both cases, remainder are same
∴ 4a + 17 = a + 4
⇒ 4a – a = 4 – 17 ⇒ 3a = -13
⇒ a = \(\frac { -13 }{ 3 }\)
Hence a = \(\frac { -13 }{ 3 }\)
Question 10.
If the polynomials ax3 + 3x2 – 13 and 2x3 – 5x + a, when divided by (x – 2), leave the same remainders, find the value of a.
Solution:
Let p(x) = ax3 + 3x2 – 13
q(x) = 2x3 –5x + a
and divisor g(x) = x – 2
x-2 = 0
⇒ x = 2
∴ Remainder = p(2) = a(2)3 + 3(2)2 – 13
= 8a + 12 – 13 = 8a – 1
and q( 2) = 2(2)3 – 5×2 + a=16-10 + a
= 6 + a
∵ In each case remainder is same
∴ 8a – 1 = 6 + a
8a – a = 6 + 1
⇒ 7a = 7
⇒ a = \(\frac { 7 }{ 7 }\)= 1
∴ a = 1
Question 11.
Find the remainder when x3 + 3x2 + 3x + 1 is divided by
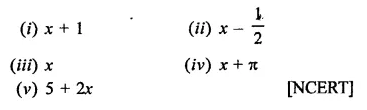
Solution:
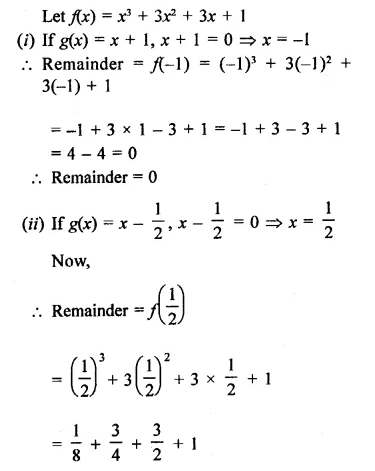
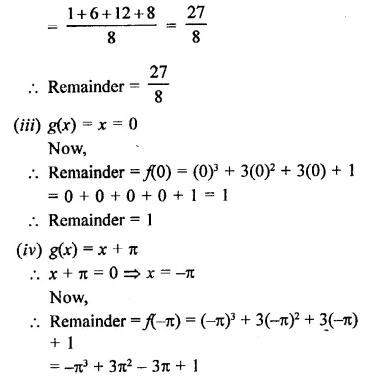
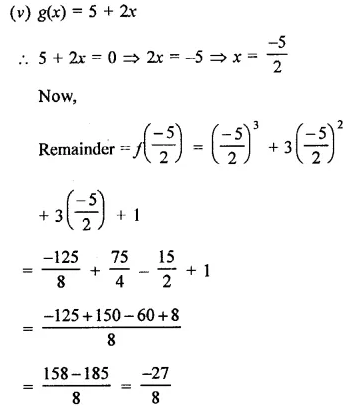
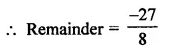
Question 12.
The polynomials ax3 + 3a-2 – 3 and 2x3 – 5x + a when divided by (x – 4) leave the remainders R1 and R2, respectively. Find the values of a in each case of the following cases, if
(i) R1 = R2
(ii) R1 + R2 = 0
(iii) 2R1 – R2 = 0.
Solution:
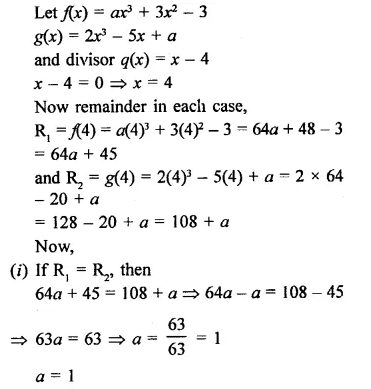
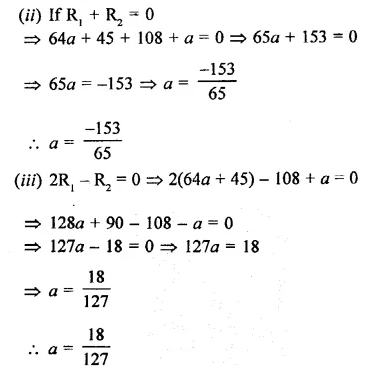
Hope given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials Ex 6.3 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.