RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials VSAQS

These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials VSAQS

Other Exercises

Question 1.
Define zero or root of a polynomial.
Solution:
A real number a is a zero or root of a polynomial f(x) if f(α) = 0

Question 2.
If x = \(\frac { 1 }{ 2 }\) is a zero of the polynomial f(x) =  8x3 + ax2 – 4x + 2, find the value of a.
Solution:
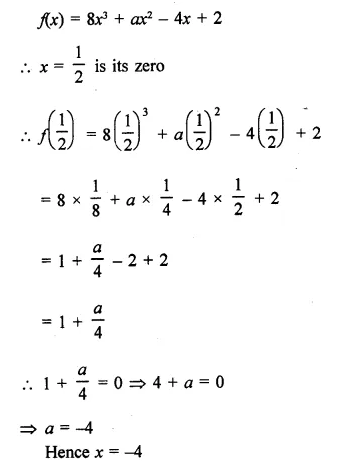
RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials VSAQS Q2.1

Question 3.
Write the remainder when the polynomial f(x) = x3+x2-3x + 2is divided by x + 1.
Solution:
f(x) = x3+x2-3x + 2
Let x + 1 = 0, then x = -1
∴ Remainder =(-1)
Now,f(-1) = (-1)3 + (-1)2 – 3(-1) + 2
= -1 + 1+ 3 + 2 = 5
∴ Remainder = 5

Question 4.
Find the remainder when x3 + 4x2 + 4x – 3 is divided by x.
Solution:
f(x) = x3 + 4x2 + 4x – 3
Dividing f(x) by x, we get
Let x = 0, then
f(x) = 0 + 0 + 0 – 3 = -3
∴  Remainder = -3

Question 5.
If x + 1 is a factor of x3 + a, then write the value of a.
Solution:
Let f(x) = x3 + a
∴ x + 1 is a factor of fx)
Let x + 1 = 0
⇒ x = -1
∴ f(-1) = x3 + a
= (-1)3 + a = -1 + a
∴  x + 1 is a factor
∴  Remainder = 0
∴  -1 + a = 0 ⇒  a = 1
Hence a = 1

Question 6.
If f(x) = x4-2x3 + 3x2 – ax – b when divided by x – 1, the remainder is 6, then find the value of a + b.
Solution:
f(x) = x4 – 2x3 + 3x2 – ax – b
Dividing f(x) by x – 1, the remainder = 6
Now let x – 1 = 0, then x = 1
∴  f(1) = (1)4 – 2(1)3 + 3(1)2 -ax 1-b
= 1 -2 + 3-a-b = 2-a-b
∴ Remainder = 6
∴ 2 – a – b = 6  ⇒ a + b = 2 – 6 = -4
Hence a + b = -4

Hope given RD Sharma Class 9 Solutions Chapter 6 Factorisation of Polynomials VSAQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.