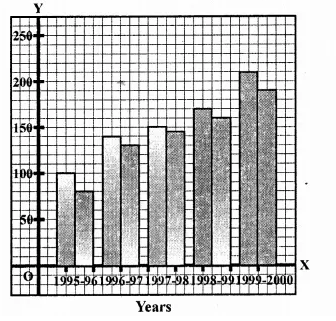
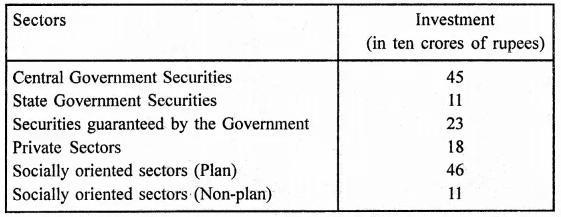
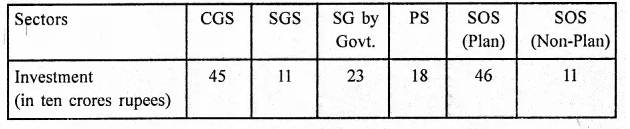
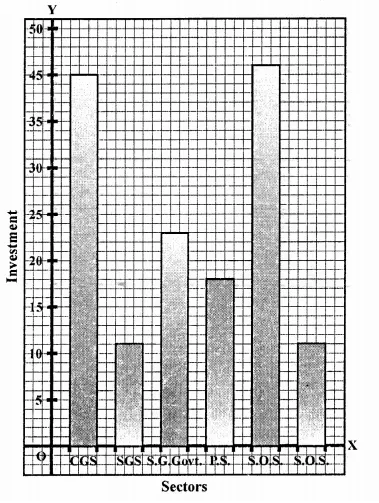
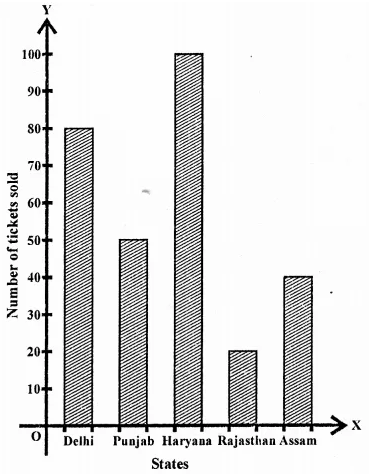
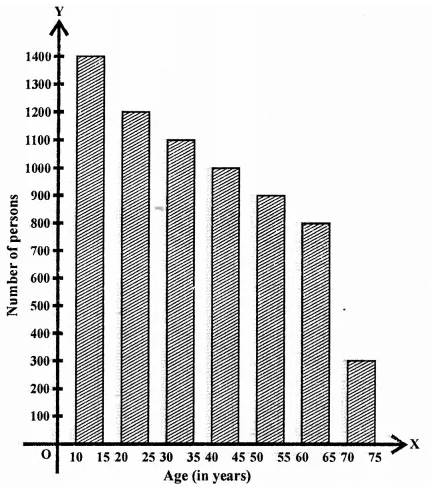
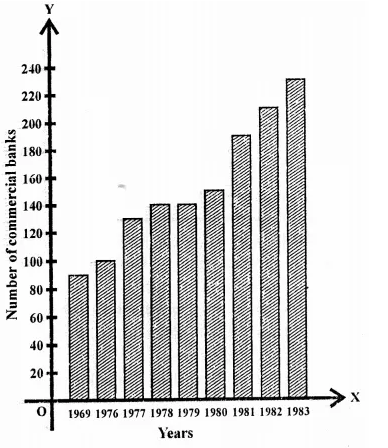
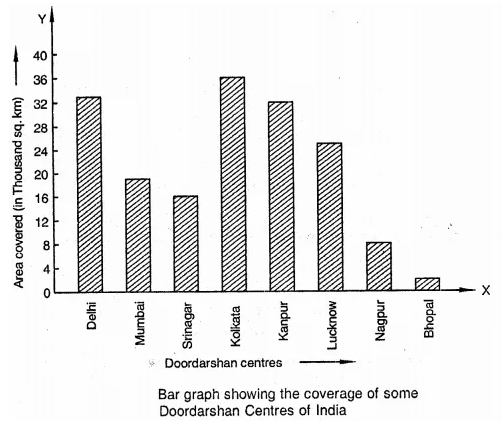
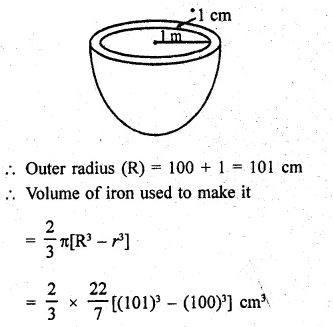
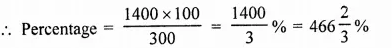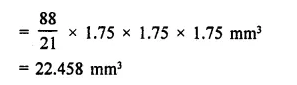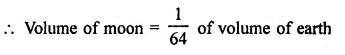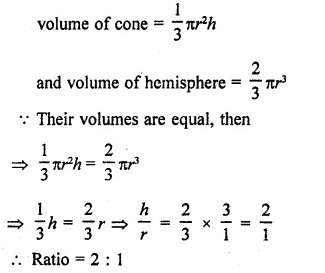RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.1
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.1
Other Exercises
- RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.1
- RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.2
- RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.3
Question 1.
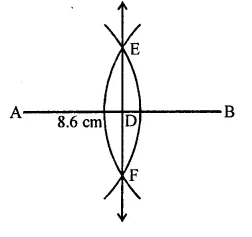
Draw a line segment of length 8.6 cm. Bisect it and measure the length of each part.
Solution:
Steps of construction :
(i) Draw a line segment AB = 8.6 cm.
(ii) With centres A and B, and radius more than half of AB, draw arcs which intersect each other at E and F, on both sides of AB.
(iii) Join EF which intersects AB at D.
D is the required mid point of AB.
Measuring each part, it is 4.3 cm long.
Question 2.
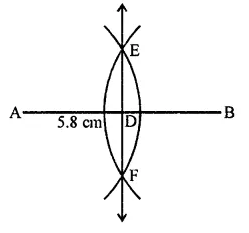
Draw a line segment AB of length 5.8 cm. Draw the perpendicular bisector of this line segment.
Solution:
Steps of construction :
(i) Draw a line segment AB = 5.8 cm.
(ii) With centres A and B and radius more than half of AB, draw arcs intersecting each other at E and F.
(iii) Join EF which is the required perpendicular bisector of AB.
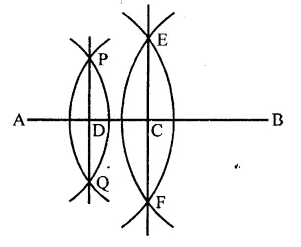
Question 3.
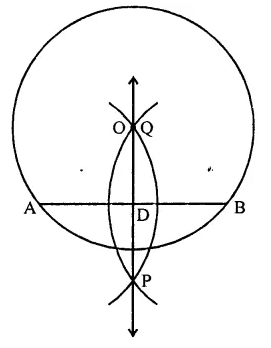
Draw a circle with centre at point O and radius 5 cm. Draw its chord AB, draw the perpendicular bisector of line segment AB. Does it pass through the centre of the circle?
Solution:
Steps of construction :
(i) Draw a circle with centre O and radius 5 cm.
(ii) Draw a chord AB of the circle.
(iii) With centres A and B and radius more than half of AB draw arcs intersecting each other at P and Q.
(iv) Join PQ which intersects AB at D and passes through O, the centre of the circle.
Question 4.
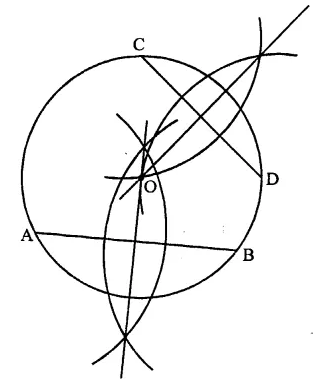
Draw a circle with centre at point O. Draw its two chords AB and CD such that AB is not parallel to CD. Draw the perpendicular bisectors of AB and CD. At what point do they intersect?
Solution:
Steps of construction :
(i) Draw a circle with centre O and a suitable radius.
(ii) Draw two chords AB and CD which are not parallel to each other.
(iii) Draw the perpendicular bisectors of AB and CD with the help of ruler and compasses. We see that these two chords intersect each other at the centre O, of the circle.
Question 5.
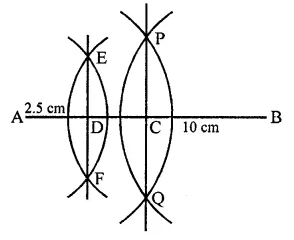
Draw a line segment of length 10 cm and bisect it. Further bisect one of the equal parts and measure its length.
Solution:
Steps of construction :
(i) Draw a line segment AB = 10 cm.
(ii) With the help of ruler and compasses, bisect AB at C.
(iii) Bisect again AC at D.
Measuring AD, it is 2.5 cm long.
Question 6.
Draw a line segment AB and bisect it. Bisect one of the equal parts to obtain a line segment of length \(\frac { 1 }{ 2 }\) (AB).
Solution:
Steps of construction :
(i) Draw a line segment AB.
(ii) With the help of ruler and compasses, draw the bisector of AB which bisects AB at C.
(iii) Similarly, in the same way draw the bisector of AC at D.
We see that AC = \(\frac { 1 }{ 2 }\) (AB).
Question 7.
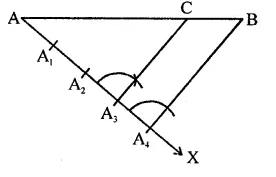
Draw a line segment AB and by ruler and compasses, obtain a line segment of length \(\frac { 3 }{ 4 }\) (AB).
Solution:
Steps of construction :
(i) Draw a line segment AB.
(ii) Draw a ray AX making an acute angle with A3 and equal 4 parts at A1, A2, A3 and A4.
(iii) JoinA4B.
(iv) From A3, draw a line parallel to A4B which meets AB at C.
C is the required point and AC = \(\frac { 3 }{ 4 }\) (AB).
Hope given RD Sharma Class 9 Solutions Chapter 16 Circles Ex 16.1 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.