RD Sharma Class 9 Solutions Chapter 25 Probability Ex 25.1
These Solutions are part of RD Sharma Class 9 Solutions. Here we have given RD Sharma Class 9 Solutions Chapter 25 Probability Ex 25.1
Other Exercises
- RD Sharma Class 9 Solutions Chapter 25 Probability Ex 25.1
- RD Sharma Class 9 Solutions Chapter 25 Probability VSAQS
- RD Sharma Class 9 Solutions Chapter 25 Probability MCQS
Question 1.
A coin is tossed 1000 times with the following frequencies
Head : 455, Tail : 545.
Compute the probability for each event.
Solution:
Total number of events (m) 1000
(i) Possible events (m) 455
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 455 }{ 1000 } \)
= \(\frac { 91 }{ 200 } \) = 0.455
(ii) Possible events (m) = 545
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 545 }{ 1000 } \) = \(\frac { 109 }{ 200 } \) = 0.545
Question 2.
Two coins are tossed simultaneously 500 times with the following frequencies of different
outcomes:
Two heads : 95 times
One tail : 290 times
No head: 115 times
Find the probability of occurrence of each of these events.
Solution:
Two coins are tossed together simultaneously 500 times
∴ Total outcomes (n) 500
(i) 2 heads coming (m) = 95 times
∴Probability P(A) = \(\frac { m }{ n } \)
= \(\frac { No. of possible events }{ Total number of events } \)
= \(\frac { 95 }{ 500 } \) = \(\frac { 19 }{ 100 } \) = 0.19
(ii) One tail (m) = 290 times
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 290 }{ 500 } \) = \(\frac { 580 }{ 1000 } \) = \(\frac { 58 }{ 100 } \) = 0.58
(iii) No head (m) = 115 times
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 115 }{ 500 } \) = \(\frac { 23 }{ 100 } \) = 0.23
Question 3.
Three coins are tossed simultaneously 1oo times with the following frequencies of different outcomes:

If the three coins are simultaneously tossed again, compute the probability of:
(i) 2 heads coming up.
(ii) 3 heads coming up.
(iii) at least one head coming up.
(iv) getting more heads than tails.
(v) getting more tails than heads.
Solution:
Three coins are tossed simultaneously 100 times
Total out comes (n) = 100

(i) Probability of 2 heads coming up (m) = 36
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 36 }{ 100 } \) = 0.36
(ii) Probability of 3 heads (m) = 12
ProbabilityP(A)= \(\frac { m }{ n } \) = \(\frac { 12 }{ 100 } \) = 0.12
(iii) Probability of at least one head coming up (m) = 38 + 36 + 12 = 86
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 86 }{ 100 } \) = 0.86
(iv) Probability of getting more heads than tails (m) = 36 + 12 = 48
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 48 }{ 100 } \) = 0.48
(v) Getting more tails than heads (m) = 14 + 38 = 52
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 52 }{ 100 } \) = 0.52
Question 4.
1500 families with 2 children were selected randomly and the following data were recorded:

If a family is chosen at random, compute the probability that it has:
(i) No girl
(ii) 1 girl
(iii) 2 girls
(iv) at most one girl
(v) more girls than boys
Solution:
Total number of families (n) = 1500

(i) Probability of a family having no girls (m) = 211
∴Probability P(A)= \(\frac { m }{ n } \) = \(\frac { 211 }{ 1500 } \) = 0.1406
(ii) Probability of a family having one girl (in) = 814
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 814 }{ 1500 } \) = 0.5426
(iii) Probability of a family having 2 girls (m) = 475
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 475 }{ 1500 } \) = 0.3166
(iv) Probability of a family having at the most one girls
∴m = 814 + 211 = 1025
∴Probability P(A) =\(\frac { m }{ n } \) = \(\frac { 1025 }{ 1500 } \) = 0.6833
(v) Probability of a family having more girls than boys (m) = 475
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 475 }{ 1500 } \) = 0.3166
Question 5.
In a cricket match, a batsman hits a boundary 6 times out of 30 balls he plays. Find the probability that on a ball played:
(i) he hits boundary
(ii) he does not hit a boundary.
Solution:
Total balls played (n) 30
No. of boundaries = 6
(i) When the batsman hits the boundary = 6
∴m = 6
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 6 }{ 30 } \) = \(\frac { 1 }{ 5 } \) = 0.2
(ii) When the batsman does not hit the boundary (m) = 30 – 6 = 24
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 24 }{ 30 } \) = \(\frac { 4 }{ 5 } \) = 0.8
Question 6.
The percentage of marks obtained by a student in monthly unit tests are given below:

Find the probability that the student gets:
(i) more than 70% marks
(ii) less than 70% marks
(iii) a distinction.
Solution:
Percentage of marks obtain in

(i) Probability of getting more than 70% marks (m) = In unit test II, III, V = 3
Total unit test (n) = 5
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 3 }{ 5 } \) = 0.6
(ii) Getting less then 70% marks = units test I and IV
∴m = 2
Total unit test (n) = 5
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 2 }{ 5 } \) = 0.4
(iii) Getting a distinction = In test V (76 of marks)
∴m = 1
Total unit test (n) = 5
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 1 }{ 5 } \) = 0.2
Question 7.
To know the opinion of the students about Mathematics, a survey of 200 students was conducted. The data is recorded in the following table:

Find the probability that a student chosen at random
(i) likes Mathematics
(ii) does not like it.
Solution:
Total number of students (n) = 200

(i) Probability of students who like mathematics (m) = 135
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 135 }{ 200 } \) = 0.675
(ii) Probability of students who dislike mathematics (m) = 65
∴Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 65 }{ 200 } \) = 0.325
Question 8.
The blood groups of 30 students of class IX are recorded as follows:
A, B, O, O, AB, O, A, O, B, A, O, B, A, O, O,
A, AB, O, A, A, O, O, AB, B, A, O, B, A, B, O,
A student is selected at random from the class from blood donation. Find the probability that the blood group of the student chosen is:
(i) A (ii) B (iii) AB (iv) O
Solution:
Total number of students of IX class = 30
No. of students of different blood groups
A AB B O
9 3 6 12

Question 9.
Eleven bags of wheat flour, each marked 5 kg, actually contained the following weights of flour
(in kg):
4.97, 5.05, 5.08, 5.03, 5.00, 5.06, 5.08, 4.98, 5.04, 5.07, 5.00
Find the probability that any of these bags chosen at random contains more than 5 kg of flour.
Solution:
Number of total bags (n) = 11
No. of bags having weight more than 5 kg (m) = 7
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 7 }{ 11 } \)
Question 10.
Following table shows the birth month of 40 students of class IX.

Find the probability that a student was born in August.
Solution:
Total number of students (n) = 40

Number of students who born in Aug. (m) = 6
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 6 }{ 40 } \) = \(\frac { 3 }{ 20 } \)
Question 11.
Given below is the frequency distribution table regarding the concentration of sulphur dioxide in the air in parts per million of a certain city for 30 days.

Find the probability of concentration of sulphur dioxide in the interval 0.12 – 0.16 on any of these days.
Solution:
Total number of days (n) = 30

Probability of cone, of S02 of the interval 0.12-0.16 (m) = 2
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 2 }{ 30 } \) = \(\frac { 1 }{ 15 } \)
Question 12.
A company selected 2400 families at random and survey them to determine a relationship between income level and the number of vehicles in a home. The information gathered is listed in the table below:
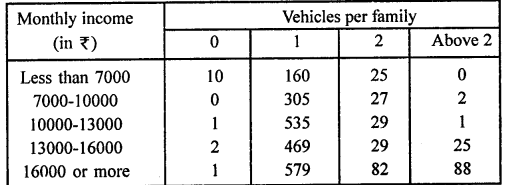
If a family is chosen, find the probability that the family is:
(i)earning Rs 10000-13000 per month and owning exactly 2 vehicles.
(ii)earning Rs 16000 or more per month and owning exactly I vehicle.
(iii)earning less than Rs 7000 per month and does not own any vehicle.
(iv)earning Rs 13000-16000 per month and owning more than 2 vehicle.
(v)owning not more than 1 vehicle.
(vi)owning at least one vehicle.
Solution:
Total number of families (n) = 2400
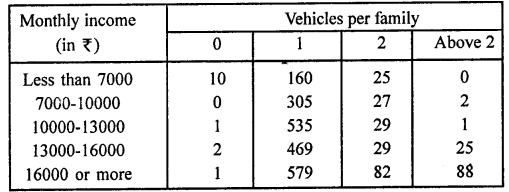
(i) Number of families earning income Rs 10000-13000 and owning exactly 2 vehicles (m) = 29
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 29 }{ 2400 } \)
(ii) Number of families earning income Rs 16000 or more having one vehicle (m) = 579
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 579 }{ 2400 } \)
(iii) Number of families earning income less than Rs 7000 having no own vehicle (m) = 10
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 10 }{ 2400 } \) = \(\frac { 1 }{ 240 } \)
(iv) Number of families having X13000 to X16000 having more than two vehicles (m) = 25
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 25 }{ 2400 } \) = \(\frac { 1 }{ 96 } \)
(v) Number of families owning not more than one vehicle (m)
= 10 + 1 + 2 + 1 + 160 + 305 + 533 + 469 + 579 = 2062
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 2062 }{ 2400 } \) = \(\frac { 1031 }{ 1200 } \)
(vi) Number of families owning at least one vechile (m) = 2048 + 192 + 110 = 2356
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 2356 }{ 2400 } \) = \(\frac { 589 }{ 600 } \)
Question 13.
The following table gives the life time of 400 neon lamps:

A bulb is selected at random. Find the probability that the life time of the selected bulb is: (i) less than 400 (ii) between 300 to 800 hours (iii) at least 700 hours.
Solution:
Total number of neon lamps (n) = 400

A bulb is chosen:
(i)No. of bulbs having life time less than 400 hours (m) = 14
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 14 }{ 400 } \) = \(\frac { 7 }{ 200 } \)
(ii)No. of bulbs having life time between 300 to 800 hours (m) = 14 + 56 + 60 + 86 + 74 = 290
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 290 }{ 400 } \) = \(\frac { 29 }{ 40 } \)
(iii)No. of bulbs having life time at least 700 hours (m) = 74 + 62 + 48 = 184
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 184 }{ 400 } \) = \(\frac { 23 }{ 50 } \)
Question 14.
Given below is the frequency distribution of wages (in Rs) of 30 workers in a certain factory:

A worker is selected at random. Find the probability that his wages are:
(i) less than Rs 150
(ii) at least Rs 210
(iii) more than or equal to 150 but less than Rs 210.
Solution:
Number of total workers (n) = 30

A worker is selected.
(i)No. of workers having less than Rs 150 (m) = 3 + 4 = 7
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 7 }{ 30 } \)
(ii)No. of workers having at least Rs 210 (m) = 4 + 3 = 7
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 7 }{ 30 } \)
(iii)No. of workers having more than or equal to Rs 150 but less than Rs 210 = 5 + 6 + 5 = 16
Probability P(A) = \(\frac { m }{ n } \) = \(\frac { 16 }{ 30 } \) = \(\frac { 8 }{ 15 } \)
Hope given RD Sharma Class 9 Solutions Chapter 25 Probability Ex 25.1 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.