RS Aggarwal Class 10 Solutions Chapter 2 Polynomials Ex 2C

RS Aggarwal Class 10 Solutions Chapter 2 Polynomials Ex 2C

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Class 10 Solutions Chapter 2 Polynomials Ex 2C. You must go through NCERT Solutions for Class 10 Maths to get better score in CBSE Board exams along with RS Aggarwal Class 10 Solutions.

Very-Short-Answer Questions
Question 1.
Solution:
Let other zero of x² – 4x + 1 be a, then
Sum of zeros = \(\frac { -b }{ a }\) = \(\frac { -(-4) }{ 1 }\) = 4
But one zero is 2 + √3
Second zero = 4 – (2 + √3) =4 – 2 – √3 = 2 – √3

Question 2.
Solution:
Let f(x) = x² + x – p(p + 1)
= x² + (p + 1) x – px – p(p + 1)
= x(x + p + 1) – p(x + p + 1)
= (x + p + 1) (x – p)
Either x + p + 1 = 0, then x = -(p + 1)
or x – p = 0, then x = p
Hence, zeros are p and -(p + 1)

Question 3.
Solution:
p(x) = x² – 3x – m(m + 3)
= x² – (m + 3)x + mx – m(m + 3)
= x(x – m – 3) + m(x – m – 3)
= (x – m – 3)(x + m)
Either x – m – 3 = 0, then x = m + 3
or x + m = 0, then x = -m
Zeros are (m + 3), -m

Question 4.
Solution:
a and p are the zeros of a polynomial
and α + β = 6, αβ = 4
Polynomial = x² – (α + β)x + αβ = x² – (6)x + 4 = x² – 6x + 4

Question 5.
Solution:
One zero of kx² + 3x + k is 2
x = 2 will satisfy it
⇒ k(2)² + 3 x 2 + k = 0
⇒ 4k + 6 + k= 0
⇒5k + 6 = 0
⇒ 5k = -6
⇒ k = \(\frac { -6 }{ 5 }\)
Hence, k = \(\frac { -6 }{ 5 }\)

Question 6.
Solution:
3 is a zero of the polynomial 2x² + x + k
Then 3 will satisfy it
2x² + x + k = 0
⇒ 2(3)² + 3 + k = 0
⇒ 18 + 3+ k = 0
⇒ 21 + k = 0
⇒ k = -21
Hence, k = -21

Question 7.
Solution:
-4 is a zero of polynomial x² – x – (2k + 2)
Then it will satisfy the equation
x² – x – (2k + 2) = 0
⇒ (-4)2 – (-4) – 2k – 2 = 0
⇒ 16 + 4 – 2k – 2 = 0
⇒ -2k + 18 = 0
⇒ 2k = 18
k = 9

Question 8.
Solution:
1 is a zero of the polynomial ax² – 3(a – 1)x – 1
Then 1 will satisfy the equation ax² – 3(a – 1) x – 1 = 0
a(1)² – 3(a – 1) x 1 – 1 = 0
⇒ a x 1 – 3a + 3 – 1 = 0
⇒ a – 3a + 2 = 0
⇒ -2a + 2 = 0
⇒ 2a = 2
⇒ a = 1

Question 9.
Solution:
-2 is a zero of 3x² + 4x + 2k
It will satisfy the equation 3x² + 4x + 2k = 5
3(-2)² + 4(-2) + 2k = 0
⇒ 3 x 4 + 4(-2) + 2k = 0
⇒ 12 – 8 + 2k = 0
⇒ 4 + 2k=0
⇒ 2k = -4
⇒ k = -2
k = -2

Question 10.
Solution:
Let f(x) = x² – x – 6
= x² – 3x + 2x – 6
= x(x – 3) + 2(x – 3)
= (x – 3)(x + 2)
(x – 3)(x + 2) = 0
Either x – 3 = 0, then x = 3
or x + 2 = 0, then x = -2
Zeros are 3, -2

Question 11.
Solution:
Sum of zeros = 1
and polynomial is kx² – 3x + 5
Sum of zeros = \(\frac { -b }{ a }\) = \(\frac { -(-3) }{ k }\) = \(\frac { 3 }{ k }\)
\(\frac { 3 }{ k }\) = 1
⇒ k = 3
Hence, k = 3

Question 12.
Solution:
Product of zeros of polynomial x² – 4x + k is 3
Product of zeros = \(\frac { c }{ a }\)
⇒ \(\frac { k }{ 1 }\) = 3
⇒ k = 3

Question 13.
Solution:
x + a is a factor of
f(x) = 2x² + (2a + 5) x + 10
Let x + a = 0, then
Zero of f(x) = -a
Now f(-a) = 2 (-a)² + (2a + 5)(-a) + 10 = 0
2a² – 2a² – 5a + 10 = 0
⇒ 5a = 10
⇒ a = 2

Question 14.
Solution:
(a – b), a, (a + b) are the zeros of 2x³ – 6x² + 5x – 7
Sum of zeros = \(\frac { -b }{ a }\)
⇒ a – b + a + a + b = \(\frac { -(-6) }{ 2 }\)
⇒ 3a = \(\frac { 6 }{ 2 }\)
⇒ 3a = 3
⇒ a = 1

Question 15.
Solution:
f(x) = x³ + x² – ax + 6 is divisible by x² – x
Remainder will be zero
Now dividing f(x) by x² – x
Remainder = (2 – a) x + b

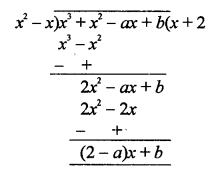
(2 – a) x + b = 0
2 – a = 0
⇒ a = 2 and b = 0
Hence, a = 2, b = 0

Question 16.
Solution:
α and β are the zeros of polynomial f(x) = 2x² + 7x + 5

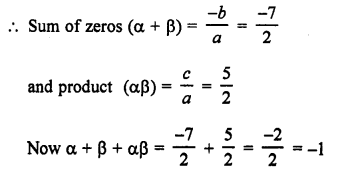
Question 17.
Solution:
Division algorithm for polynomials:
If f(x) and g(x) are any two polynomials with g(x) ≠ 0, then we can find polynomial q(x) and r(x).
f(x) = q(x) x g(x) + r(x)
where r (x) = 0
or [degree of r(x) < degree of g(x)]
or Dividend=Quotient x Division + Remainder

Question 18.
Solution:
Sum of zeros = \(\frac { -1 }{ 2 }\)
Product of zeros = -3
Polynomial: x² – (Sum of zeros) x + product of zeros

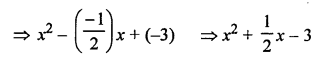
Short-Answer Questions
Question 19.
Solution:

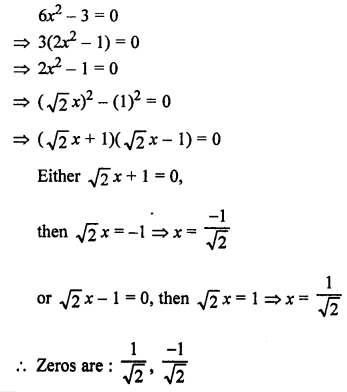
Question 20.
Solution:

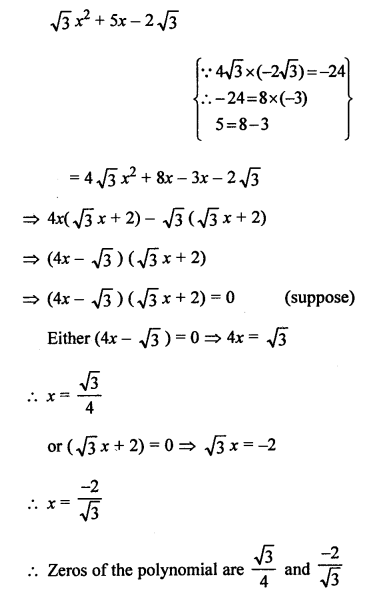
Question 21.
Solution:
α and β are the zeros of polynomial f(x) = x² – 5x + k

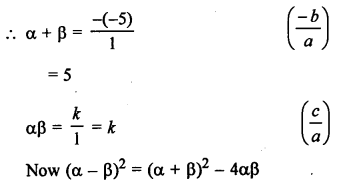
(1)² = (5)² – 4 k
1 ⇒ 25 – 4k
⇒ 4k = 25 – 1 = 24
Hence, k = 6

Question 22.
Solution:

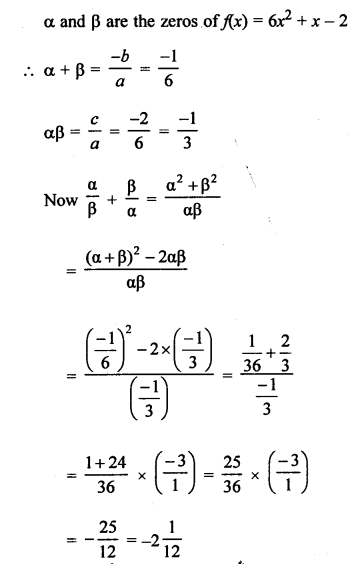
Question 23.
Solution:
α and β are the zeros of polynomial
f(x) = 5x² – 7x + 1

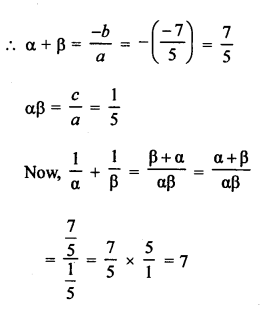
Question 24.
Solution:

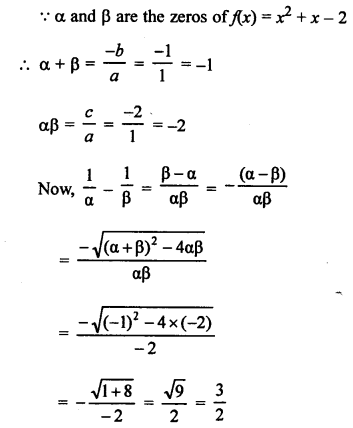
Question 25.
Solution:
(a – b), a and (a + b) are the zeros of the polynomial
f(x) = x³ – 3x² + x + 1

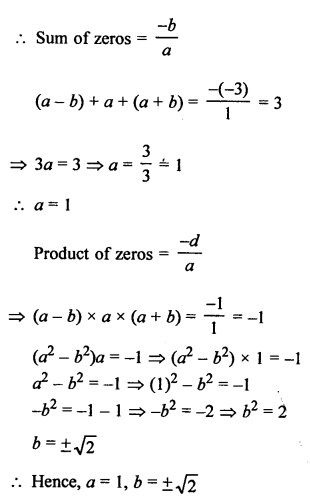
Hope given RS Aggarwal Solutions Class 10 Chapter 2 Polynomials Ex 2C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.