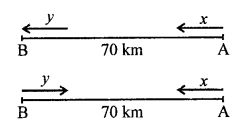
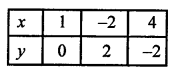
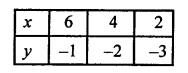
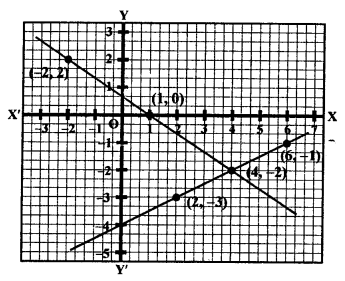
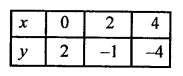
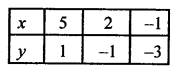
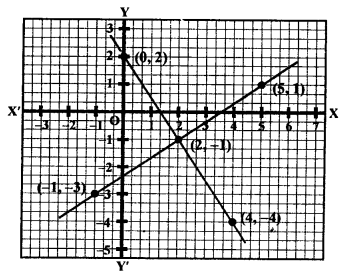
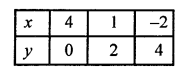
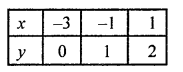
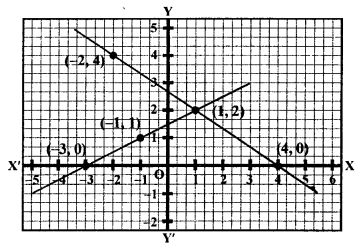
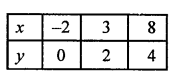
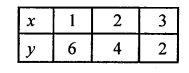
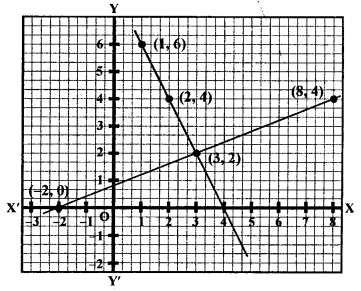
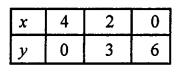
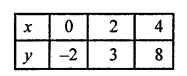
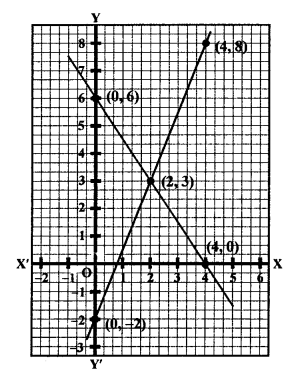
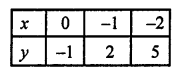
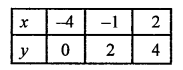
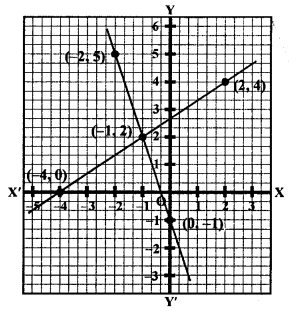
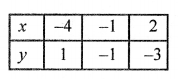
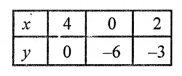
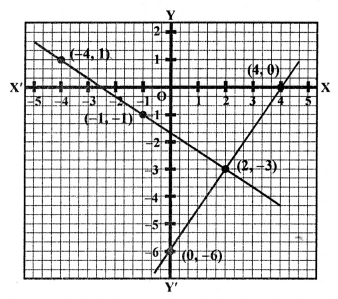
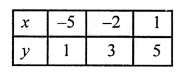
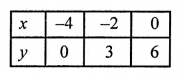
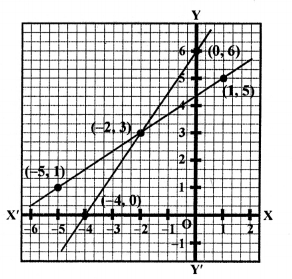
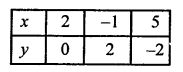
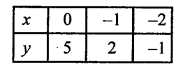
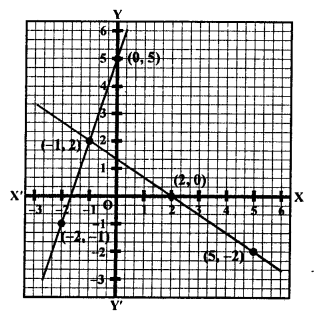
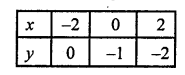
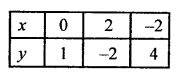
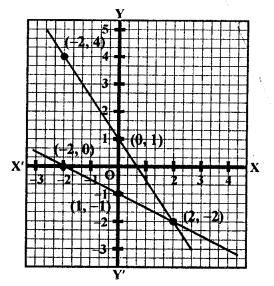
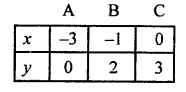
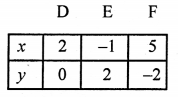
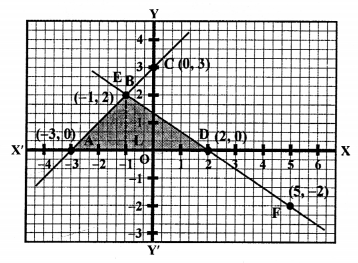
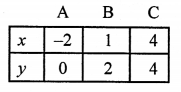
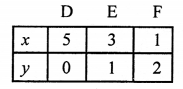
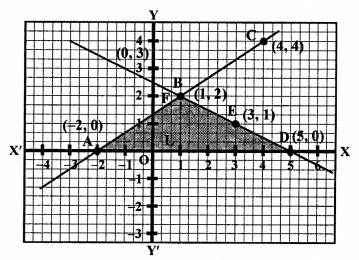
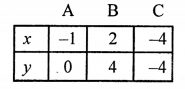
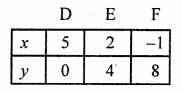
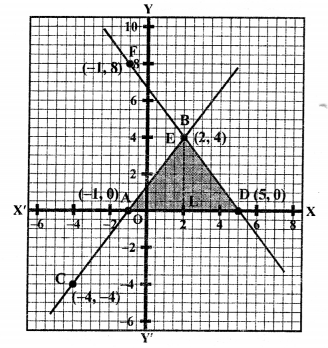
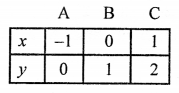
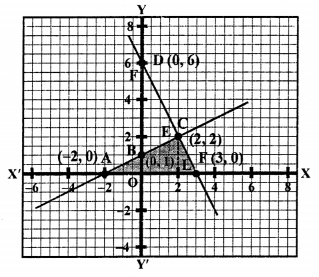
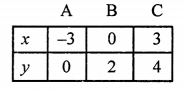
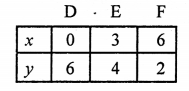
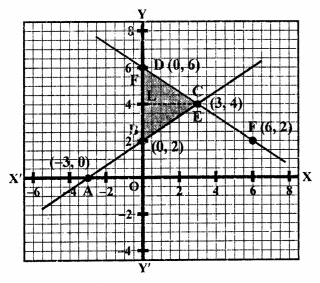
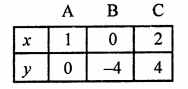
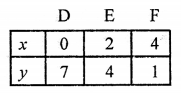
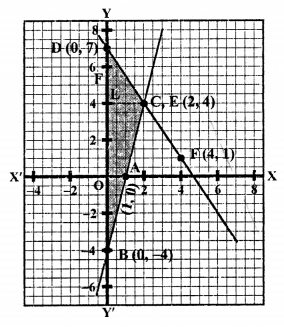
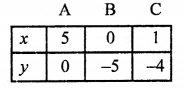
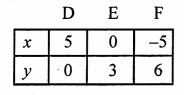
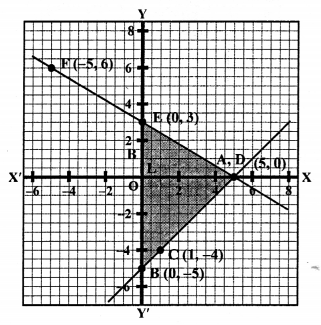
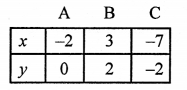
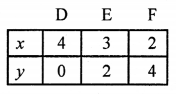
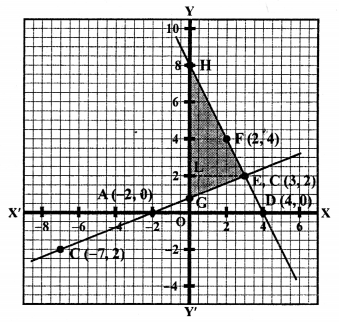
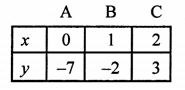
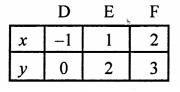
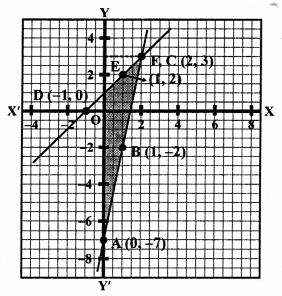
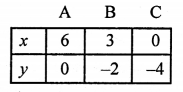
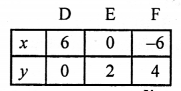
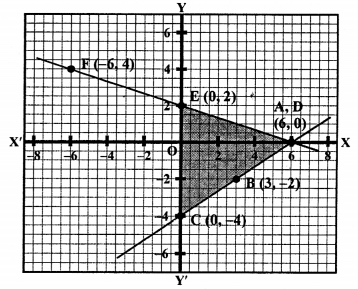
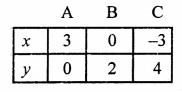
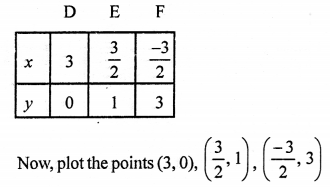
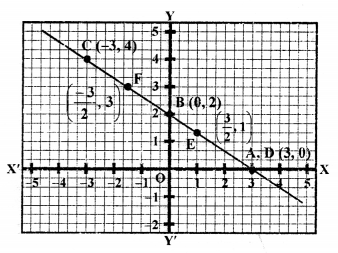
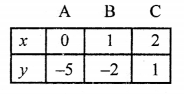
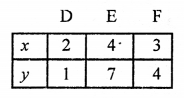
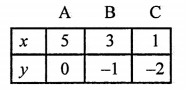
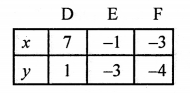
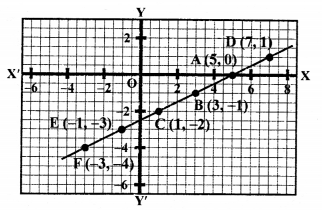
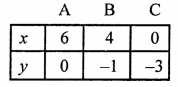
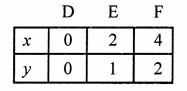
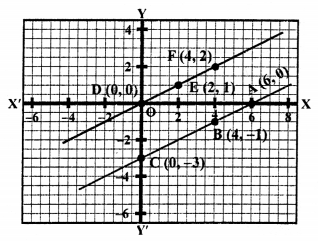
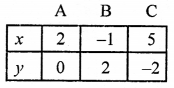
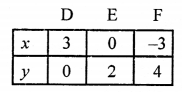
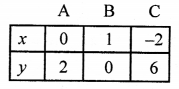
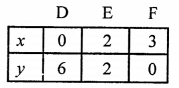
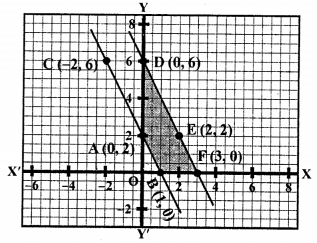
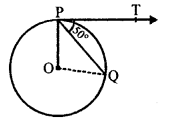
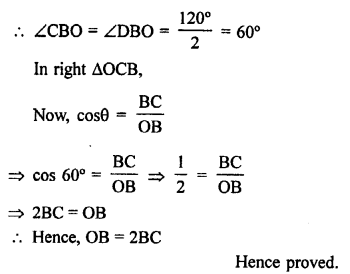
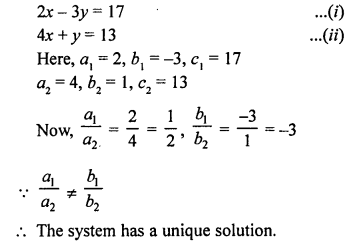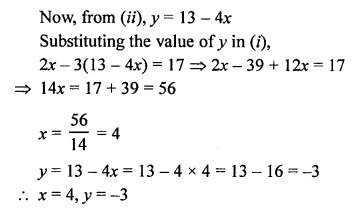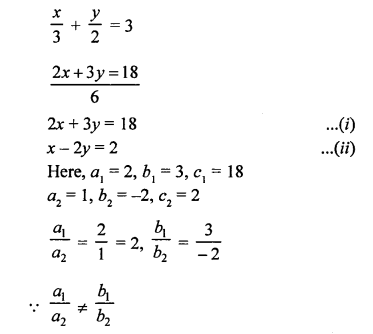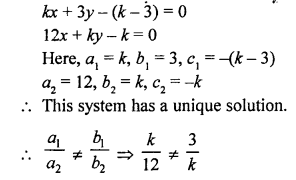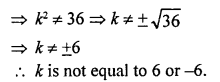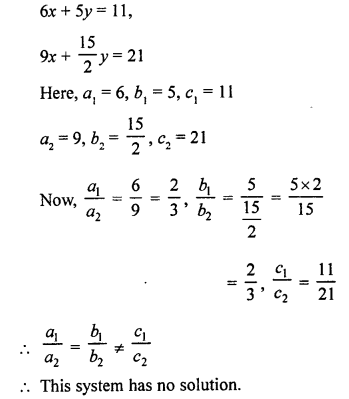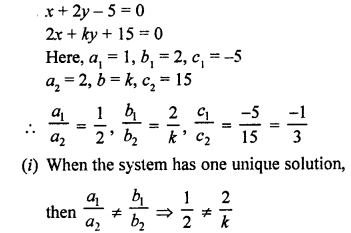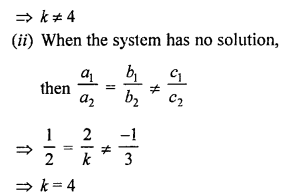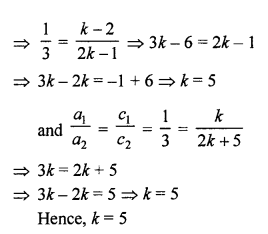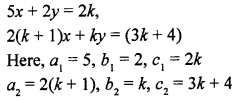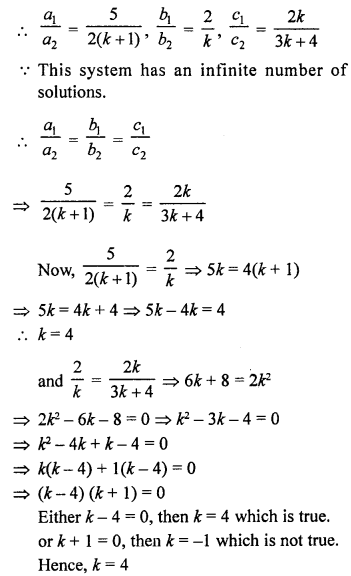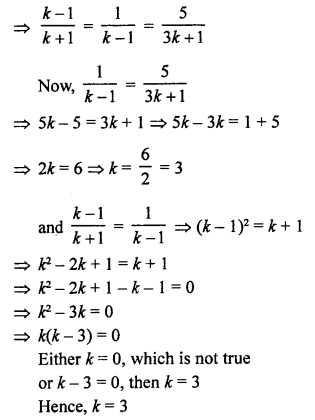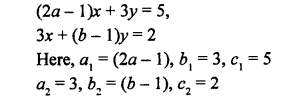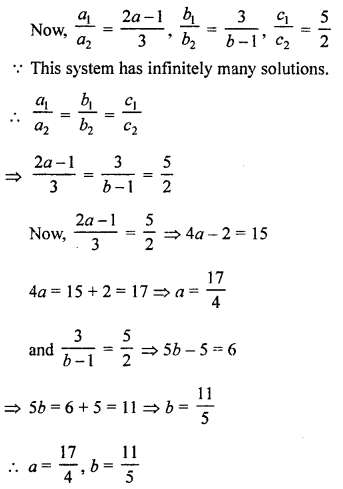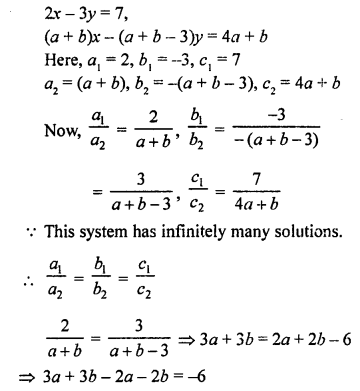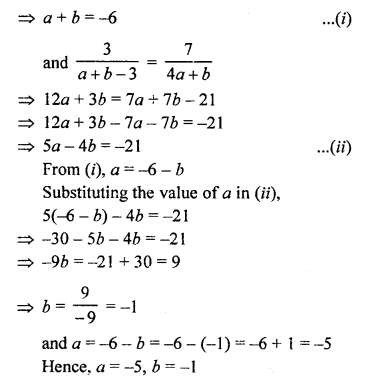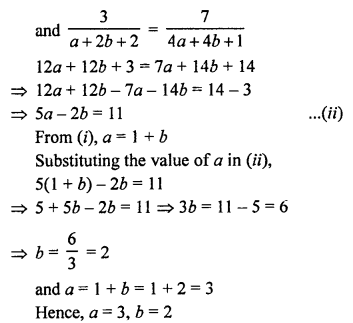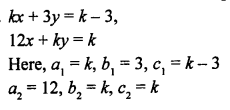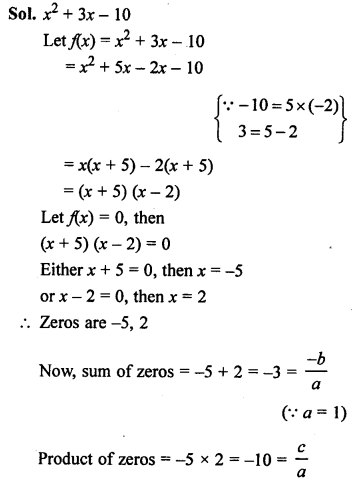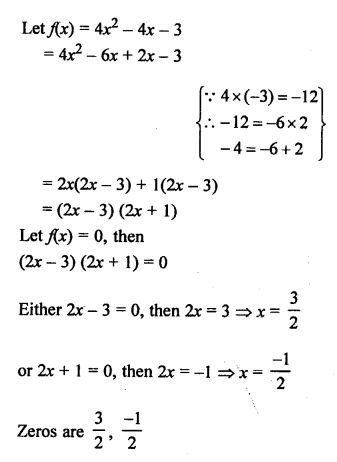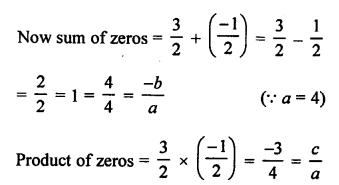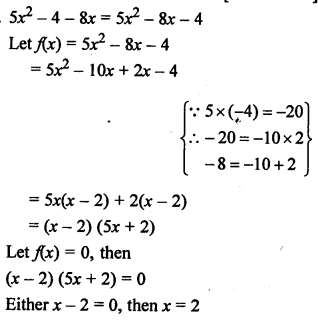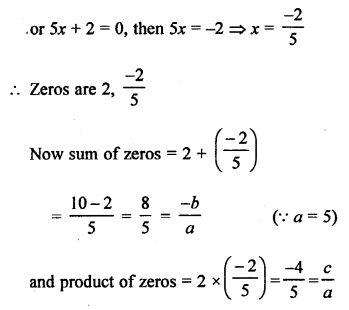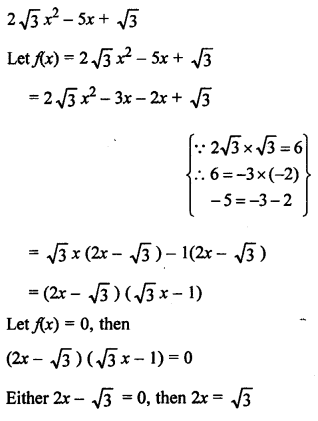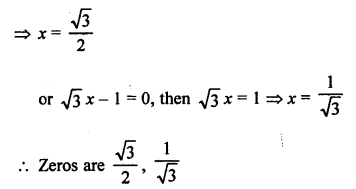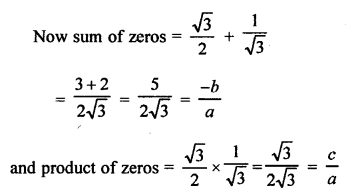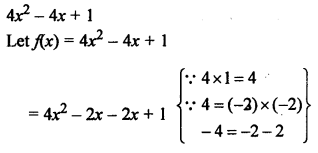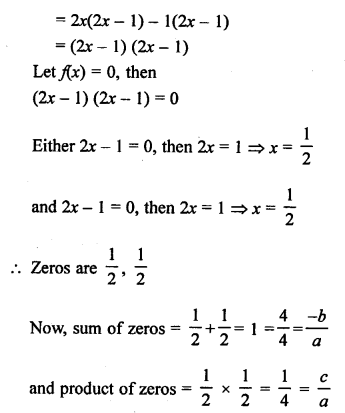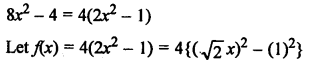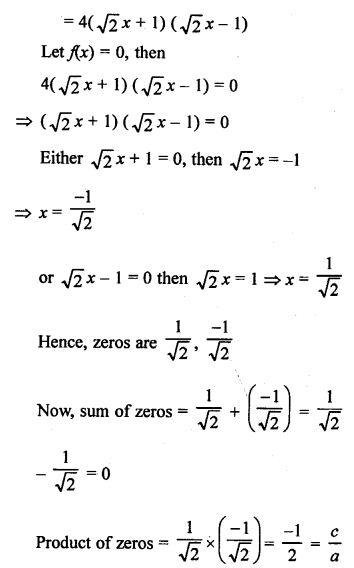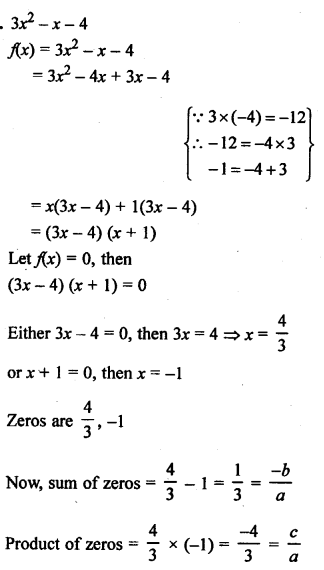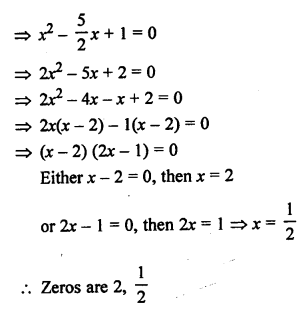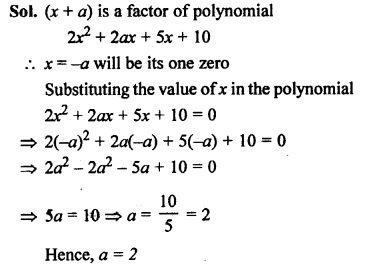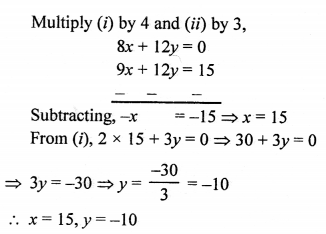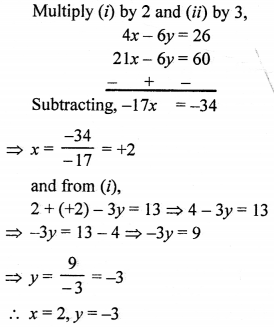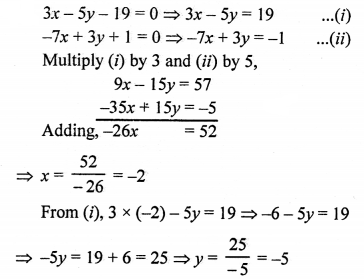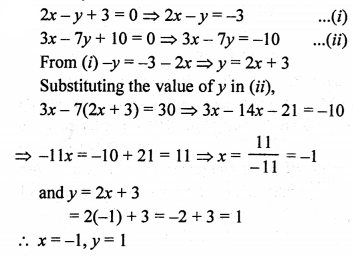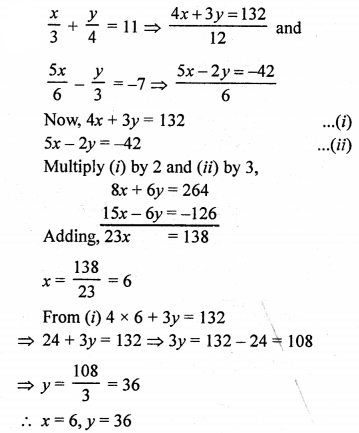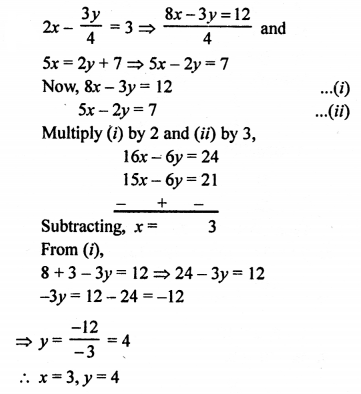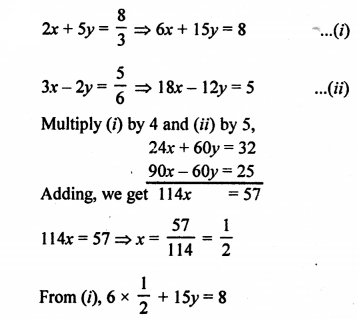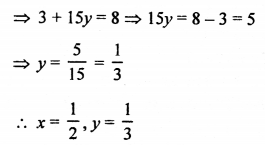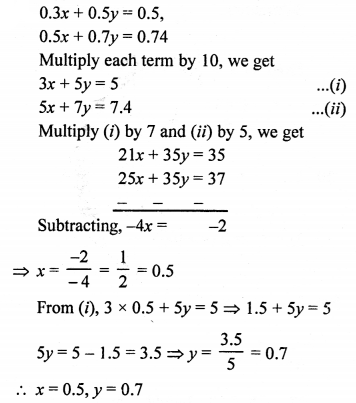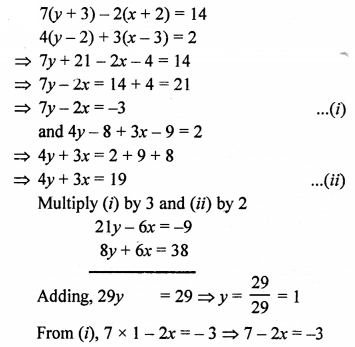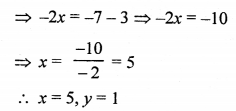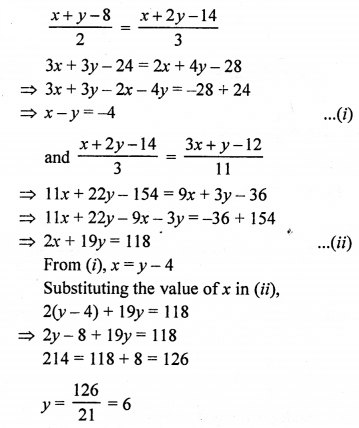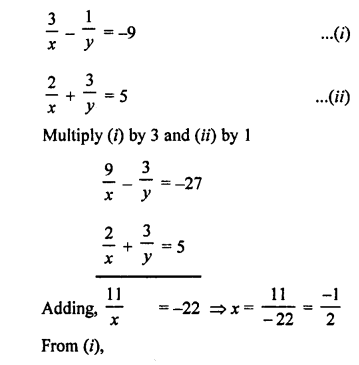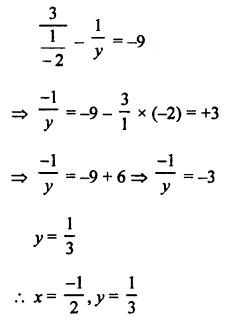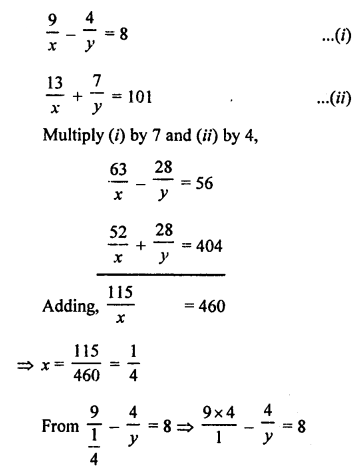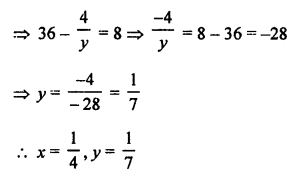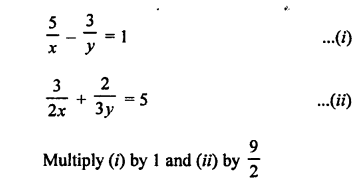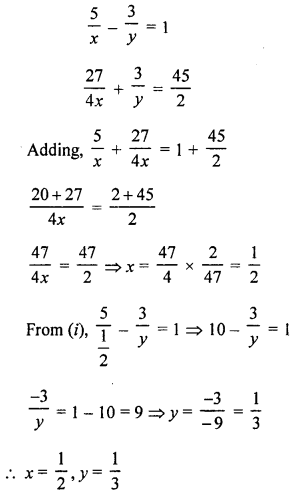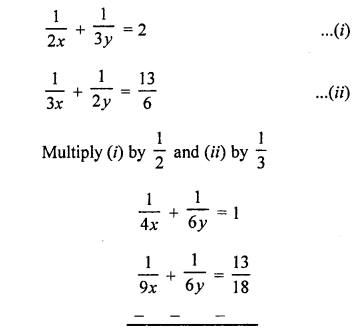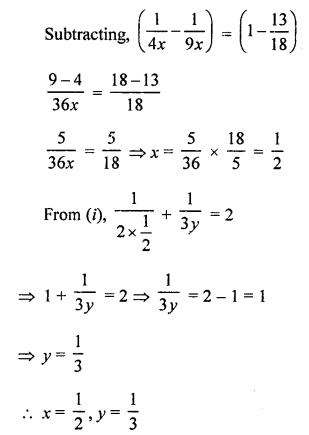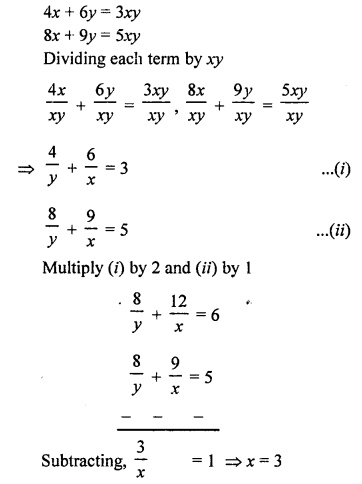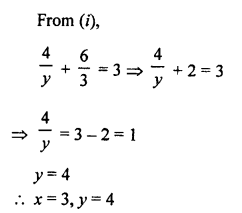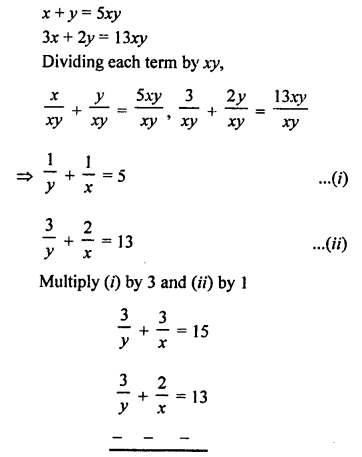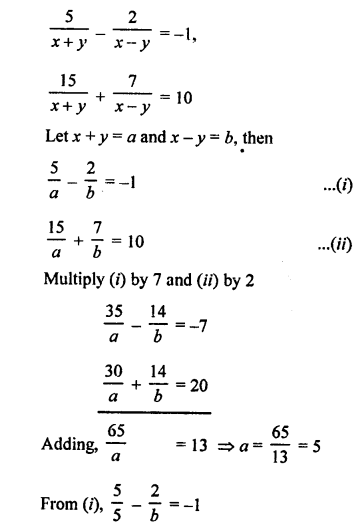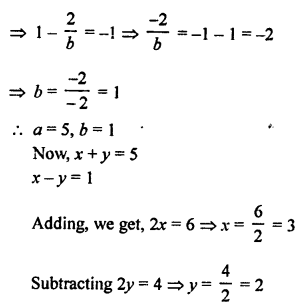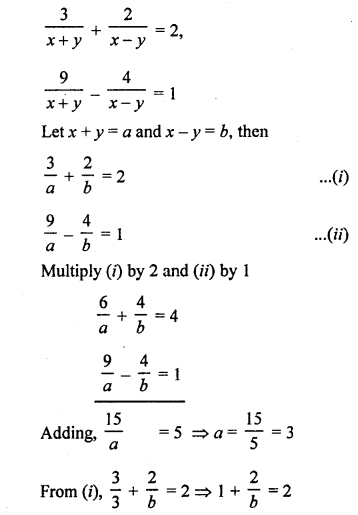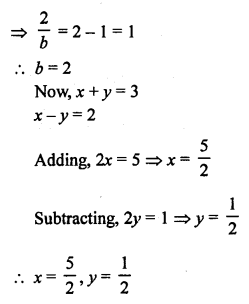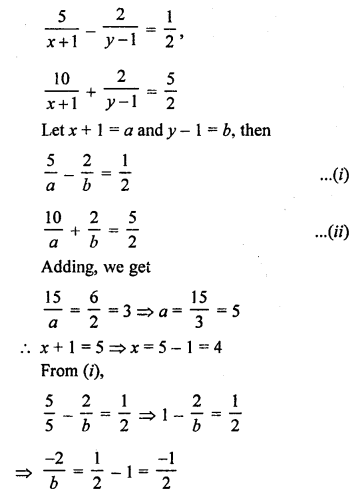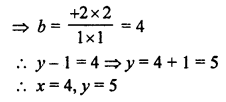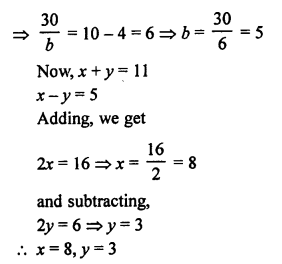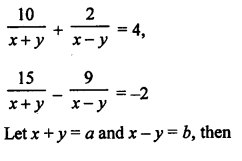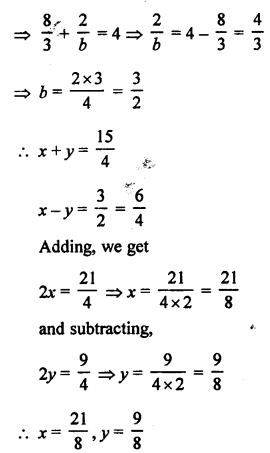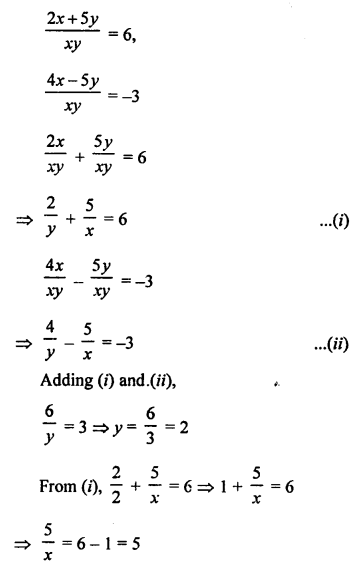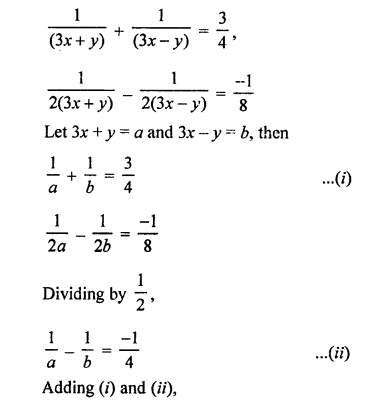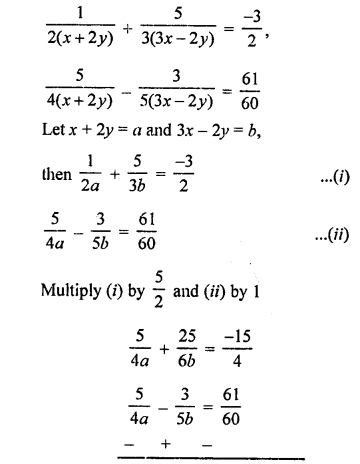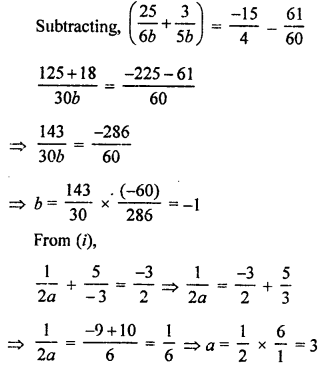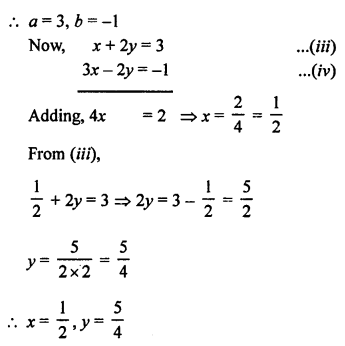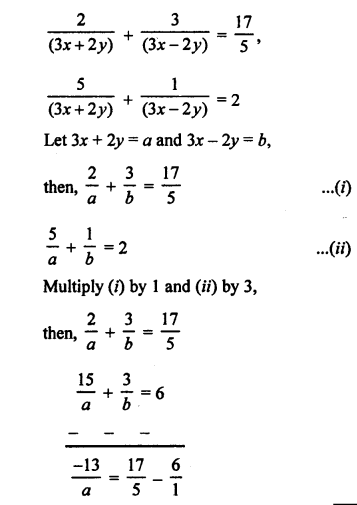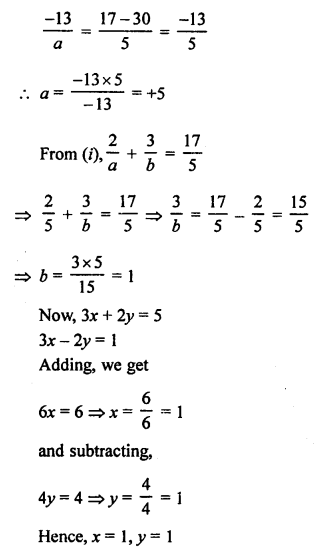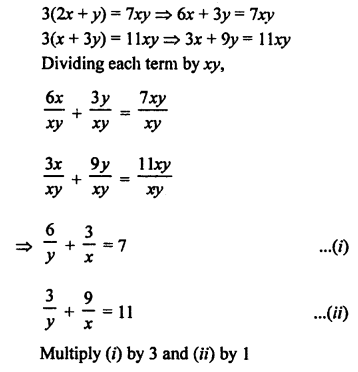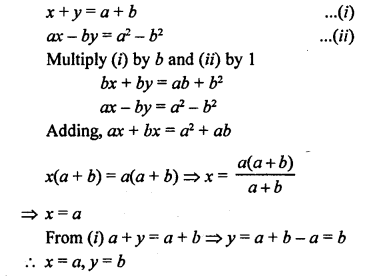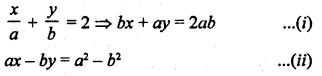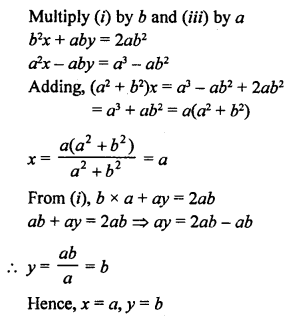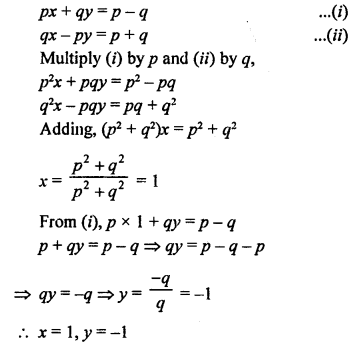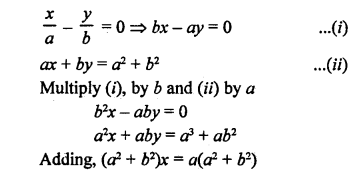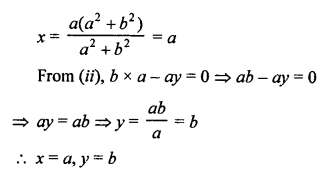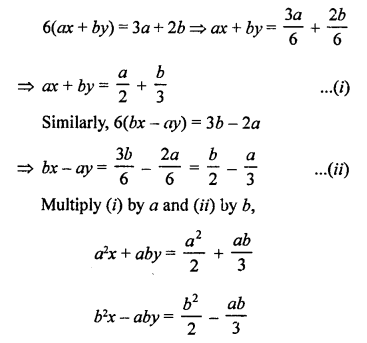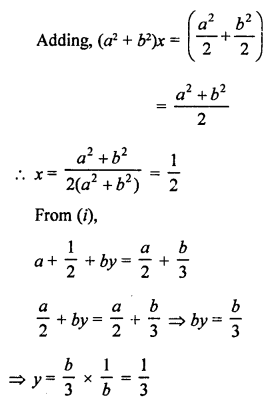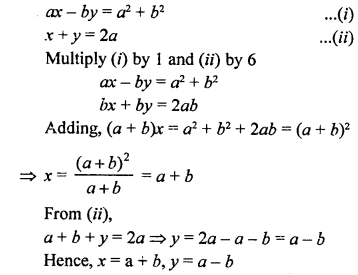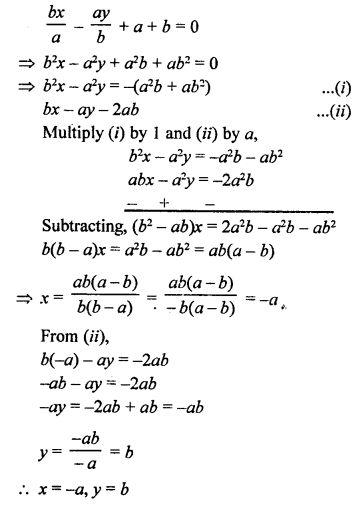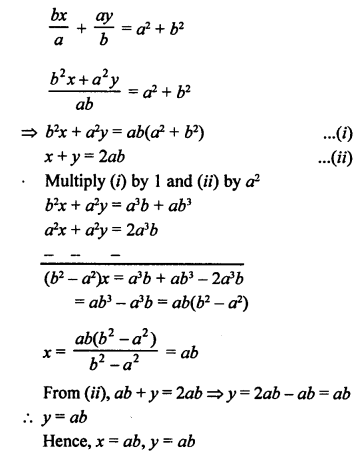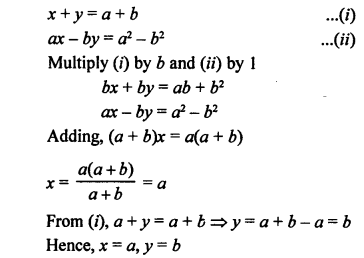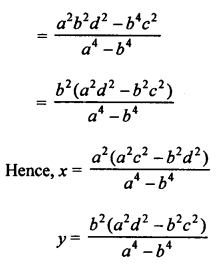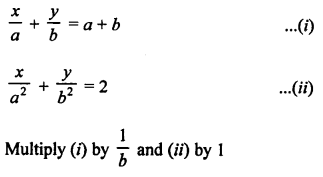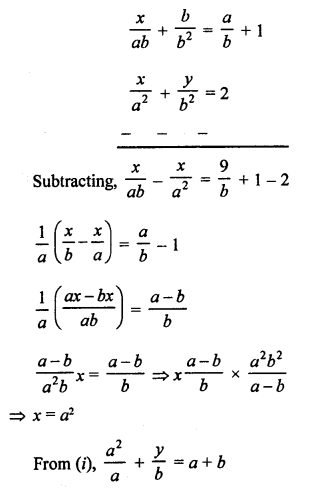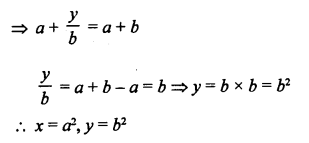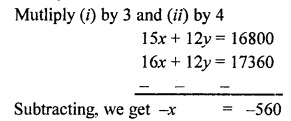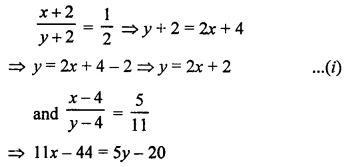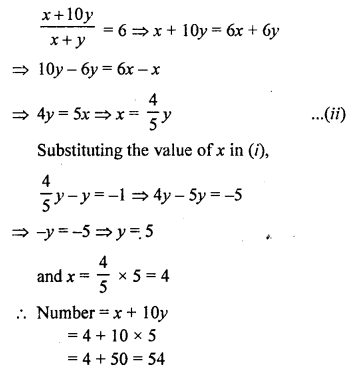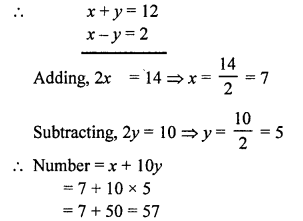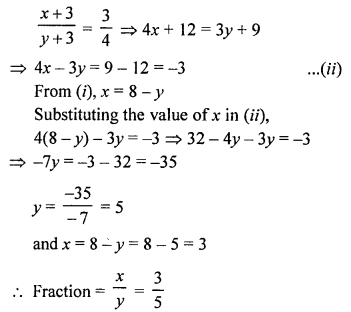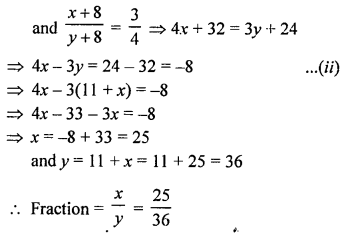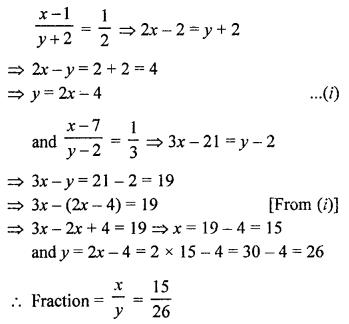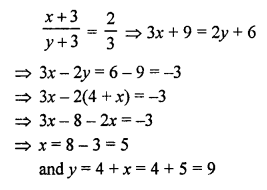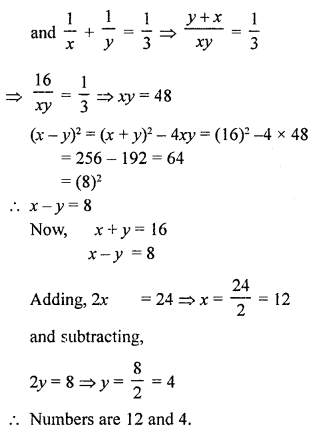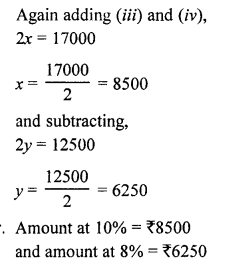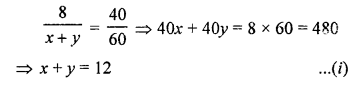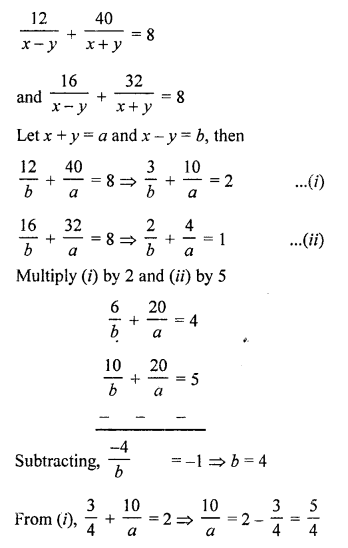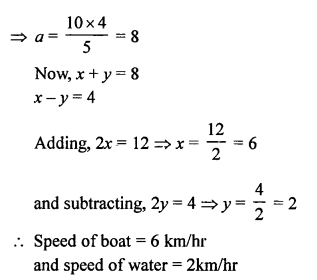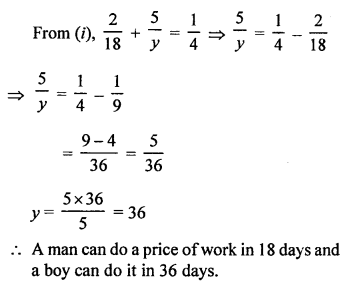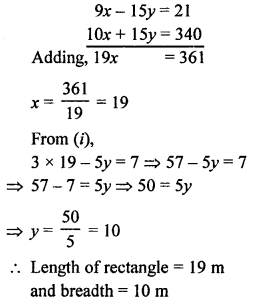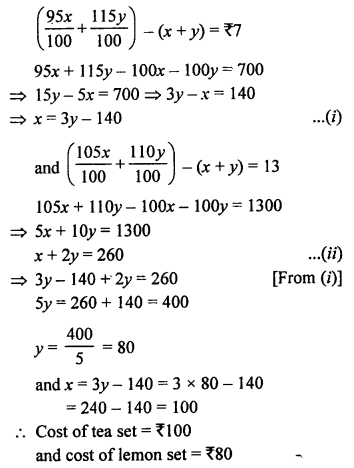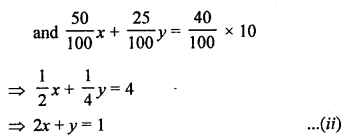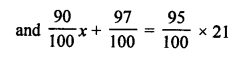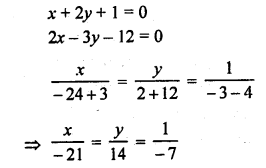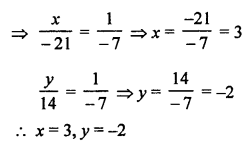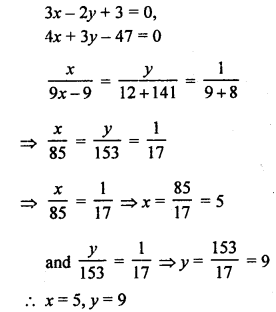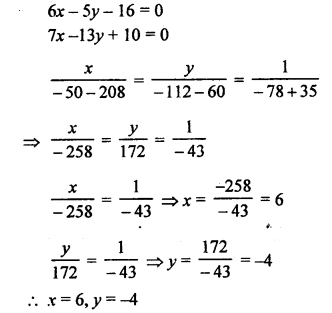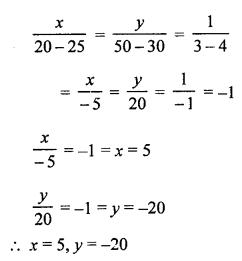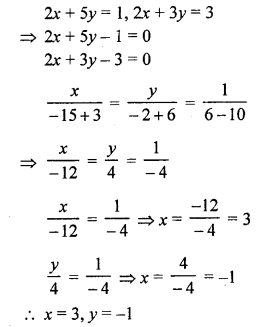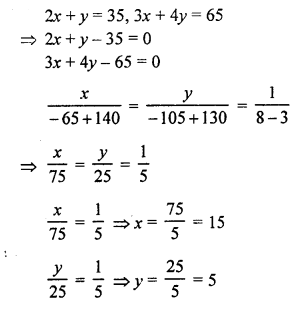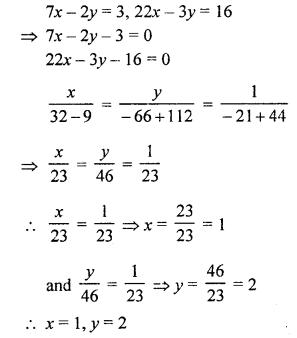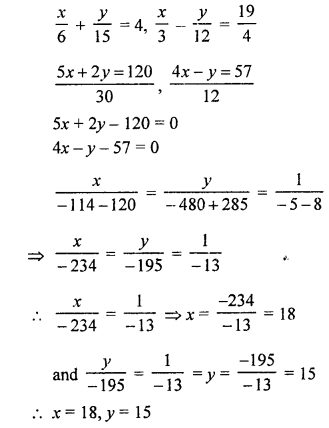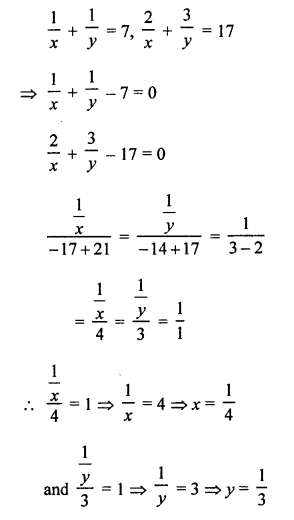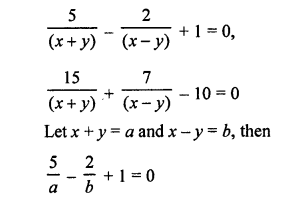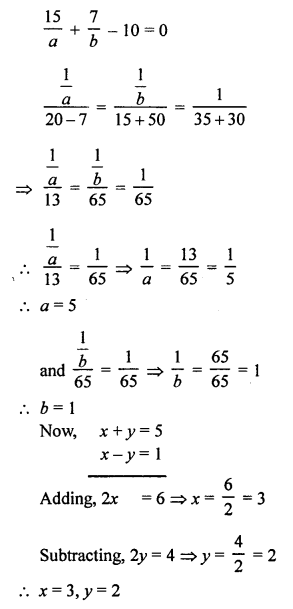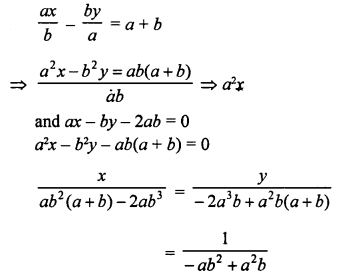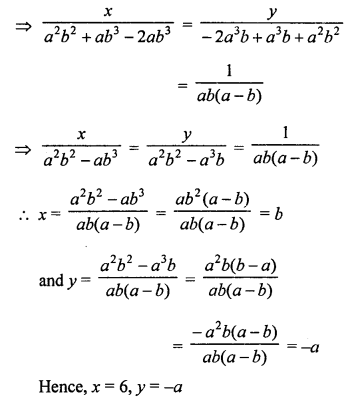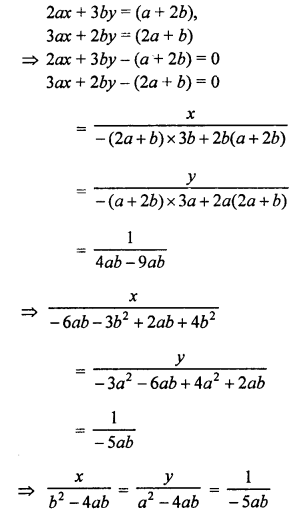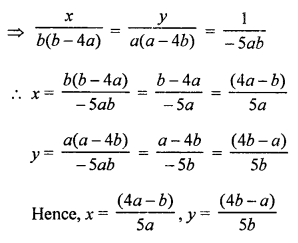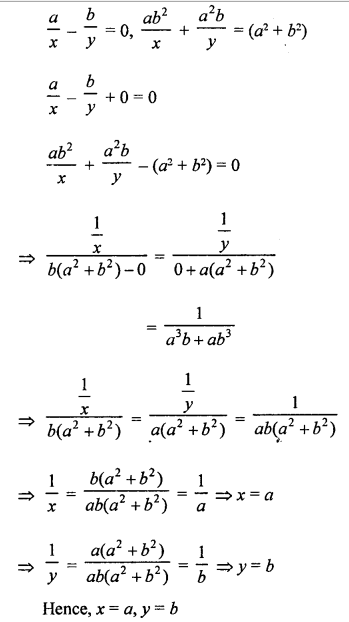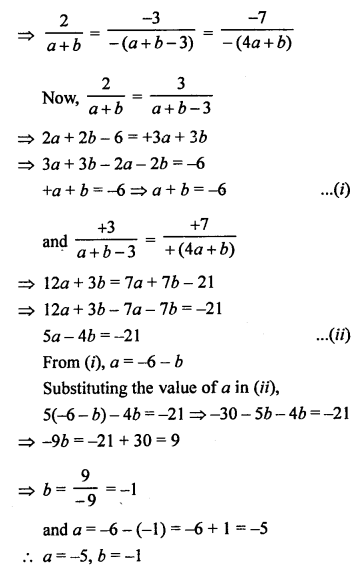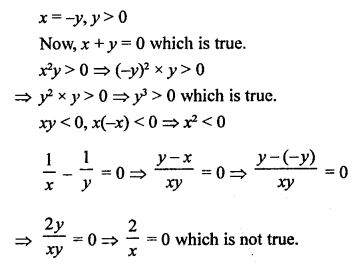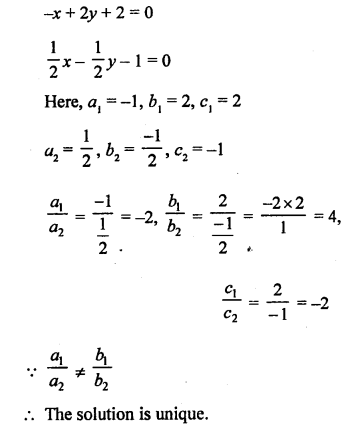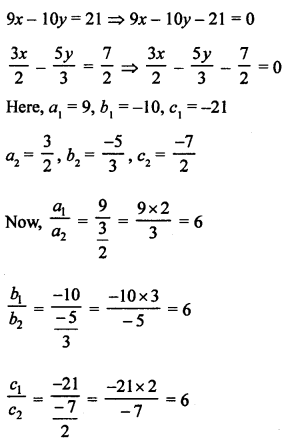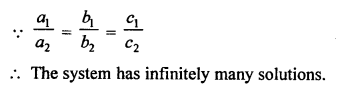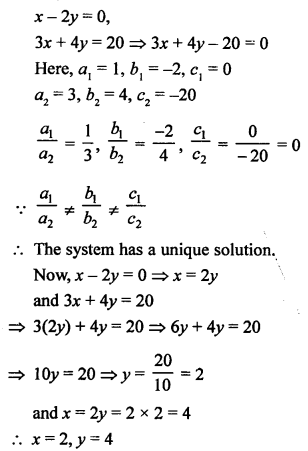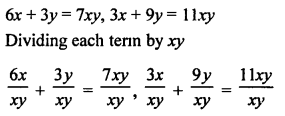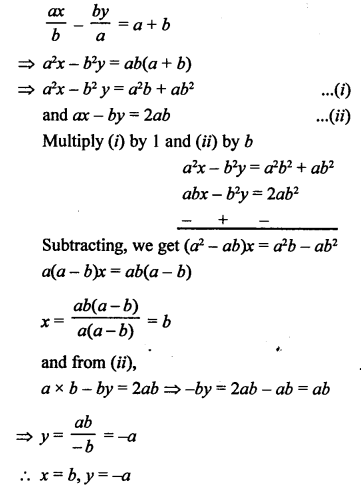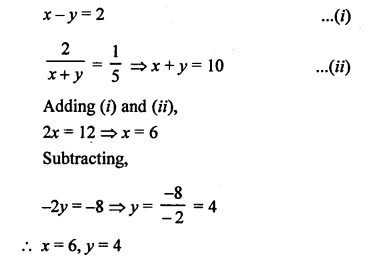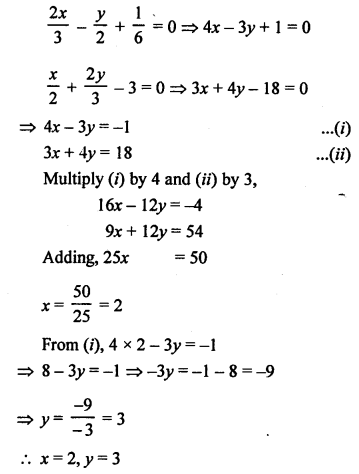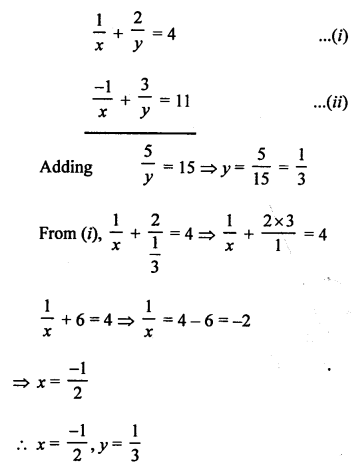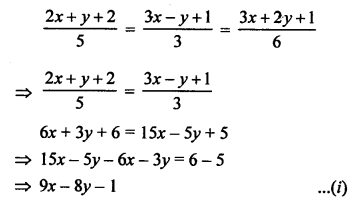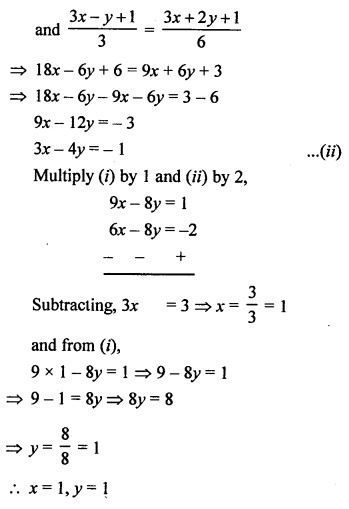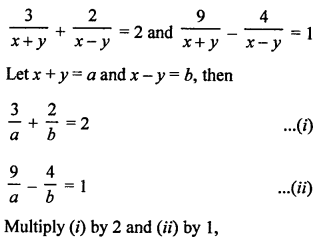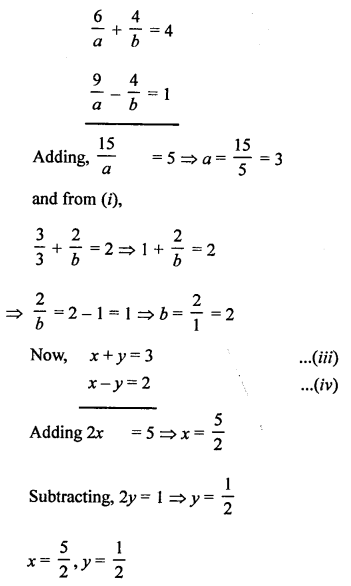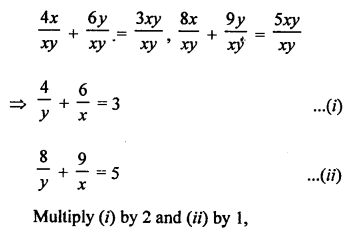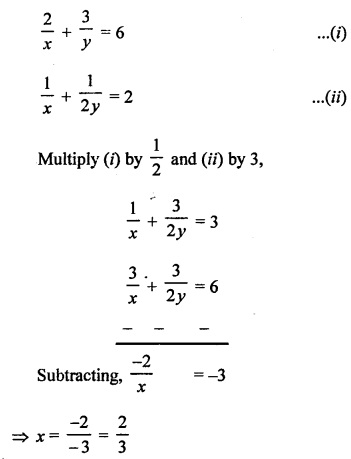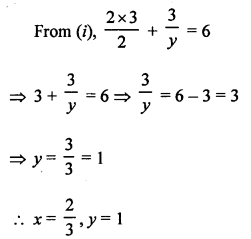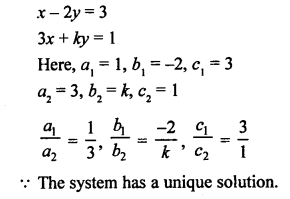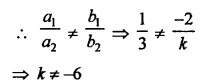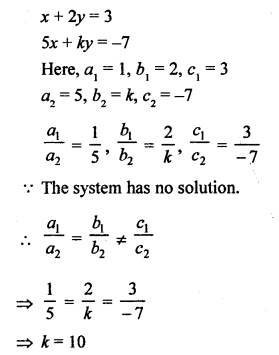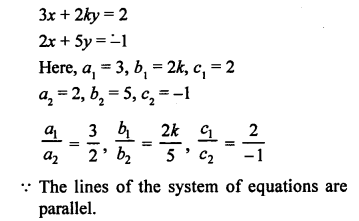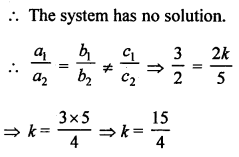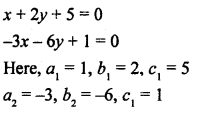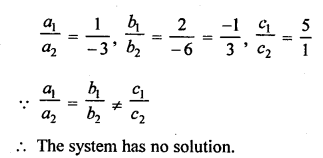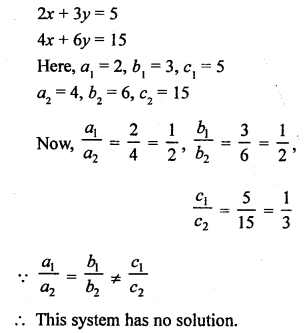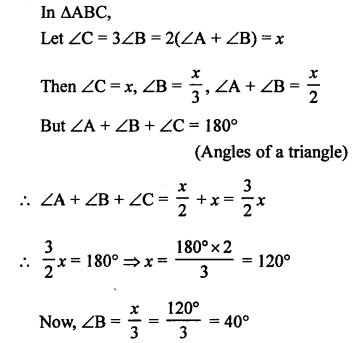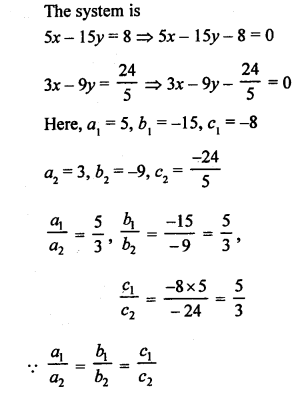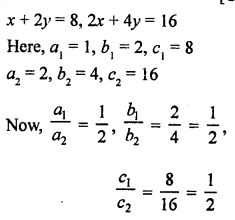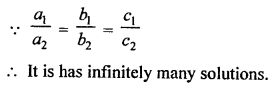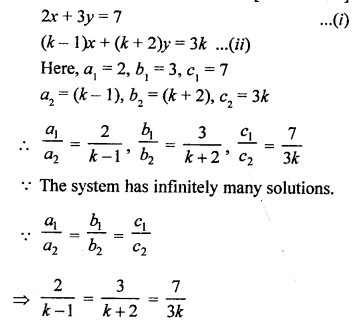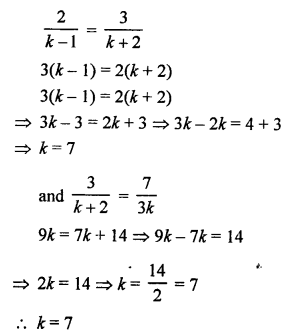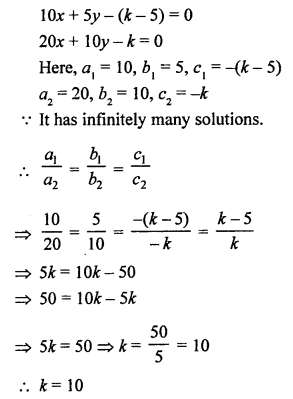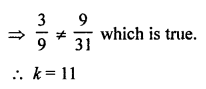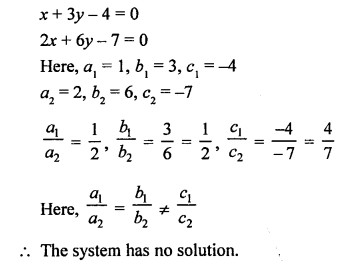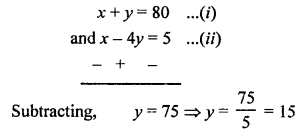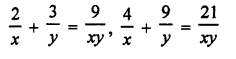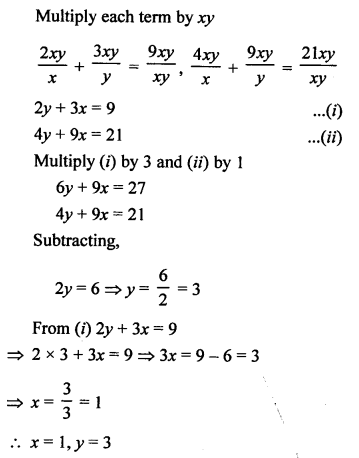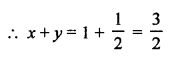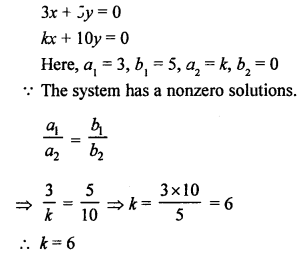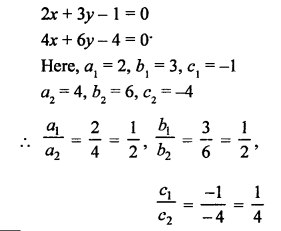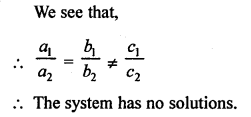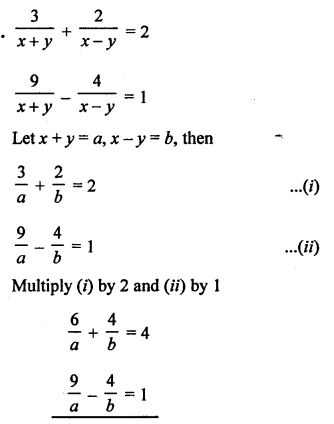NCERT Maths Solutions for Ex 4.1 class 10 Quadratic Equations is the perfect guide to boost up your preparation during CBSE 10th Class Maths Examination.
RS Aggarwal Class 10 Solutions Chapter 10 Quadratic Equations Ex 10A
These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10A.
Other Exercises
- RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10A
- RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10B
- RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10C
- RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10D
- RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10E
- RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Test Yourself
Question 1.
Solution:
We know that a second degree of equation is called a quadratic equation. Therefore,
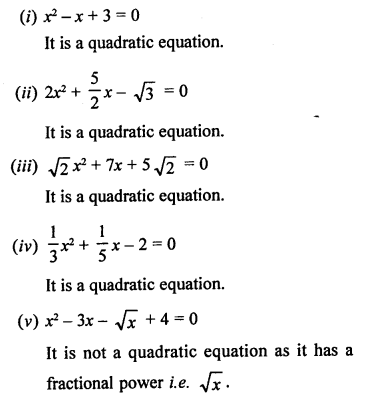
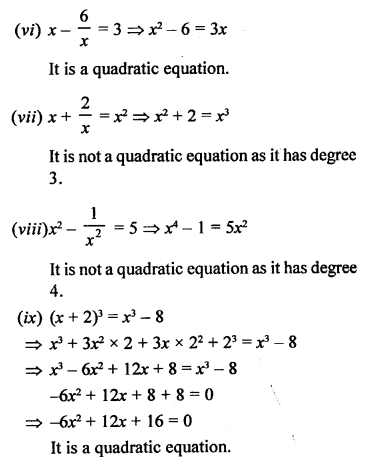
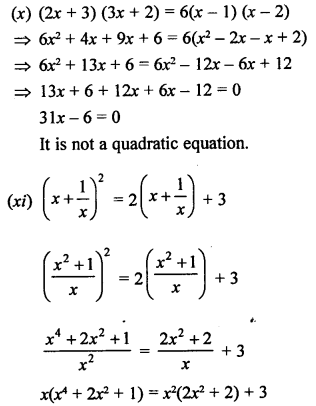
It is not a quadratic equation. It is of degree 5.
So, (i), (ii), (iii), (iv), (vi) and (ix) are quadratic equations.
Question 2.
Solution:
3x² + 2x – 1
= 3x² + 3x – x – 1
= 3x (x + 1) – 1 (x + 1)
= (x + 1) (3x – 1)
Either, x + 1 = 0 ⇒ x = -1
or 3x – 1 =0
⇒ 3x = 1
⇒ x = \(\frac { 1 }{ 3 }\)
Hence, (-1) and \(\frac { 1 }{ 3 }\) are its roots.
Question 3.
Solution:
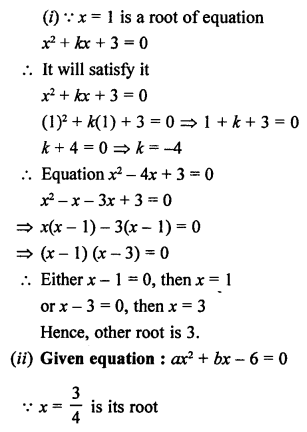

Question 4.
Solution:


Solve each of the following quadratic equations.
Question 5.
Solution:
Given : (2x – 3)(3x + 1) = 0
Either 2x – 3 = 0, then 2x = 3 ⇒ x = \(\frac { 3 }{ 2 }\)
or 3x + 1 = 0, then 3x = -1 ⇒ x = \(\frac { -1 }{ 3 }\)
x = \(\frac { 3 }{ 2 }\) , \(\frac { -1 }{ 3 }\)
Question 6.
Solution:
4×2 + 5x = 0 ⇒ x (4x + 5) = 0
Either x = 0
or 4x + 5 = 0, then 4x = -5 ⇒ x = \(\frac { -5 }{ 4 }\)
x = \(\frac { -5 }{ 4 }\) or 0
Question 7.
Solution:
3x² – 243 = 0
x² – 81 =0 (Dividing by 3)
⇒ (x)² – (9)² = 0
⇒ (x + 9) (x – 9) = 0
Either, x + 9 = 0, then x = -9
or x – 9 = 0, then x = 9
Hence, x = 9 or -9
Question 8.
Solution:
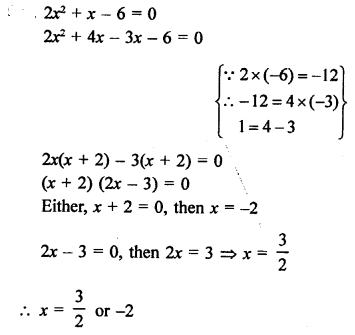
Question 9.
Solution:
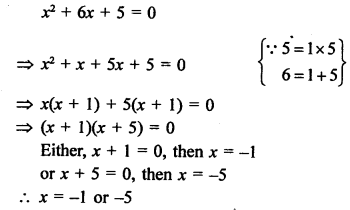
Question 10.
Solution:
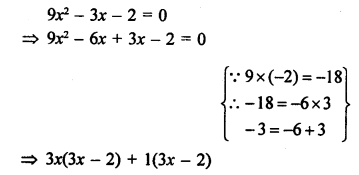
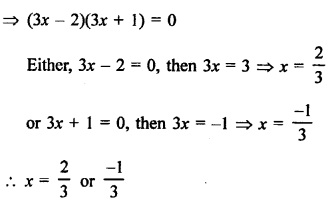
Question 11.
Solution:
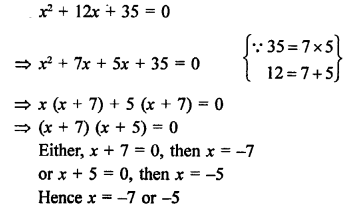
Question 12.
Solution:
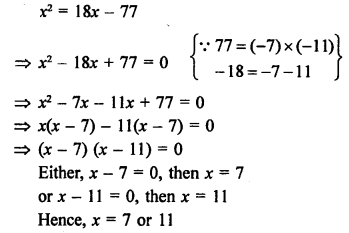
Question 13.
Solution:
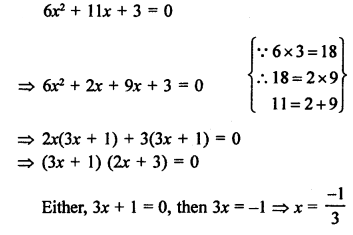
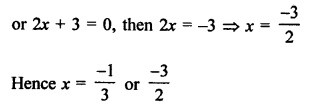
Question 14.
Solution:
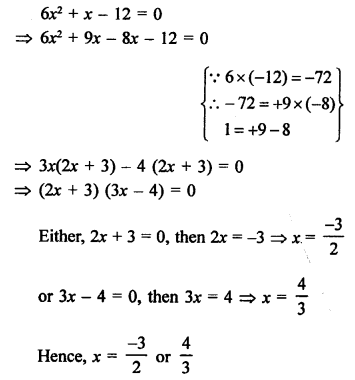
Question 15.
Solution:
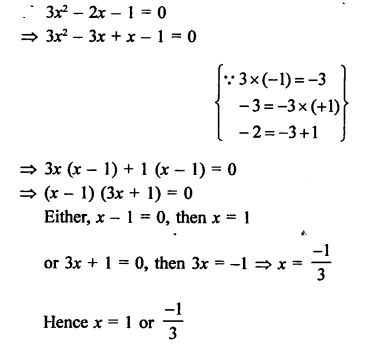
Question 16.
Solution:
4x² – 9x = 100
4x² – 9x – 100 = 0
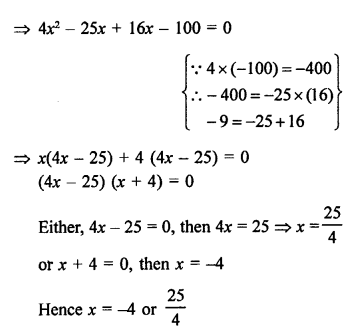
Question 17.
Solution:
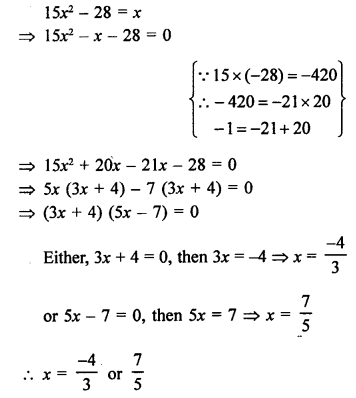
Question 18.
Solution:
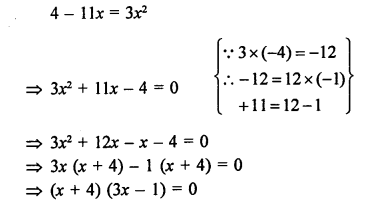
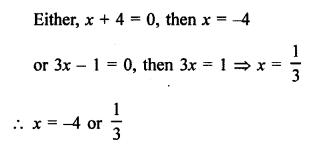
Question 19.
Solution:
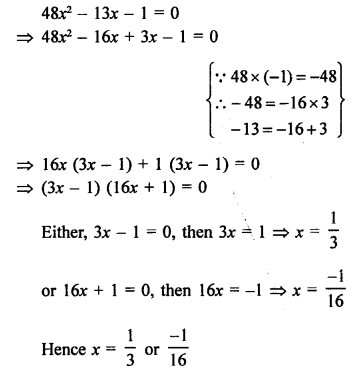
Question 20.
Solution:
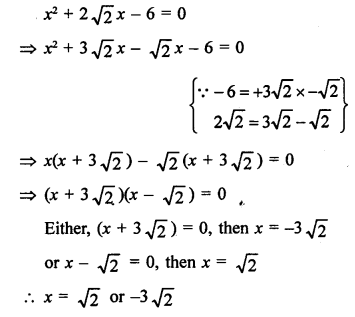
Question 21.
Solution:
√3 x² + 10x + 7√3 = 0
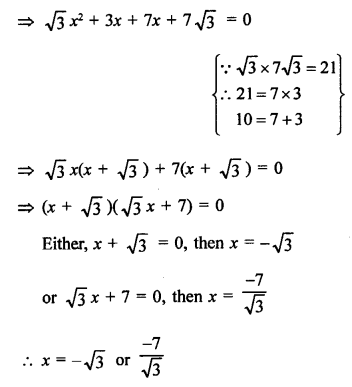
Question 22.
Solution:
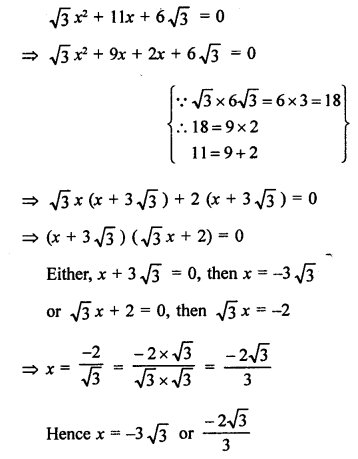
Question 23.
Solution:
3√7 x² + 4x + √7 = 0
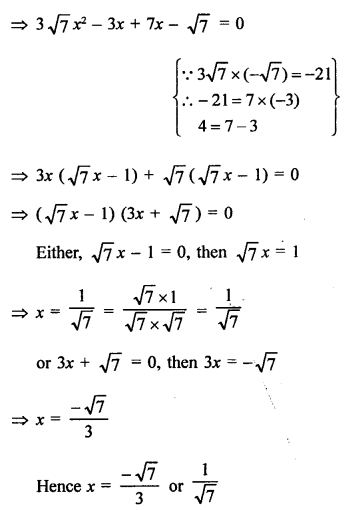
Question 24.
Solution:
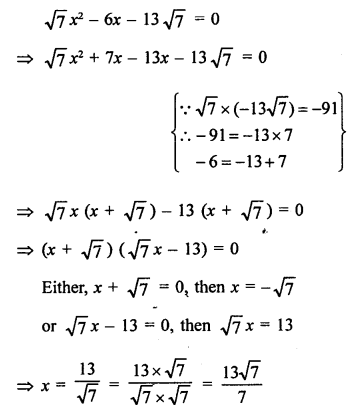
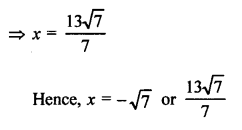
Question 25.
Solution:
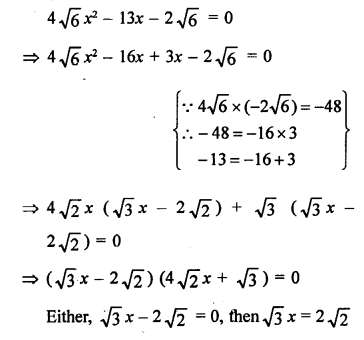
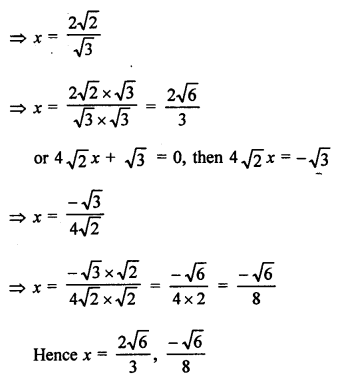
Question 26.
Solution:
3x² – 2√6x + 2 = 0
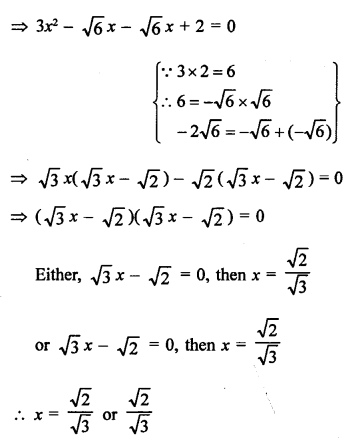
Question 27.
Solution:
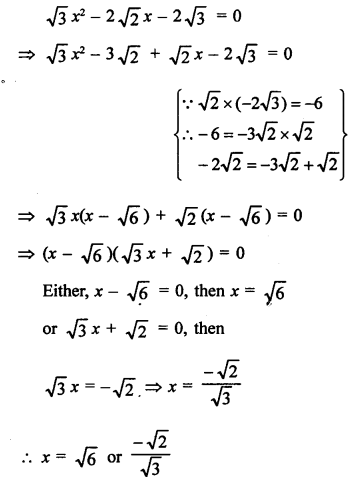
Question 28.
Solution:
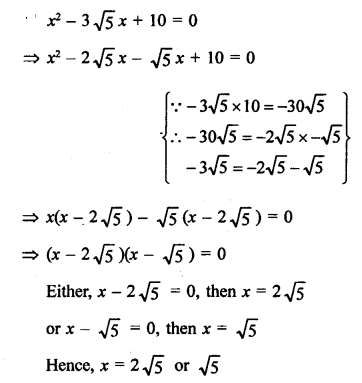
Question 29.
Solution:
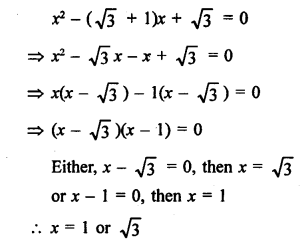
Question 30.
Solution:
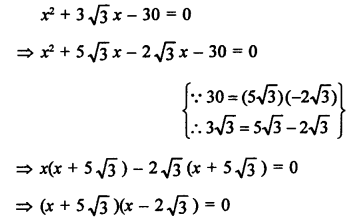
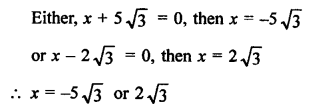
Question 31.
Solution:
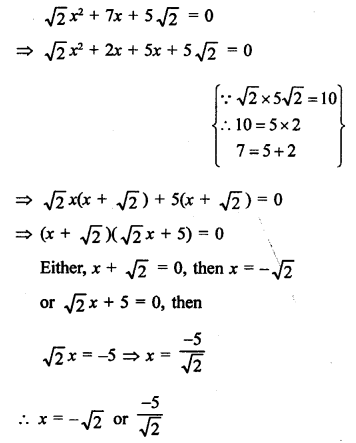
Question 32.
Solution:
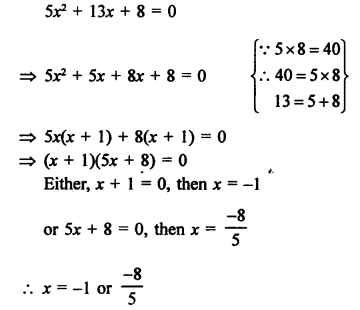
Question 33.
Solution:
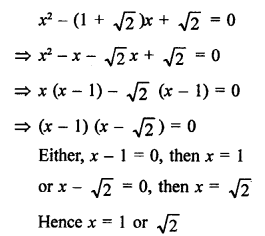
Question 34.
Solution:
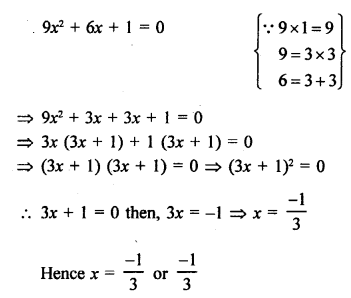
Question 35.
Solution:
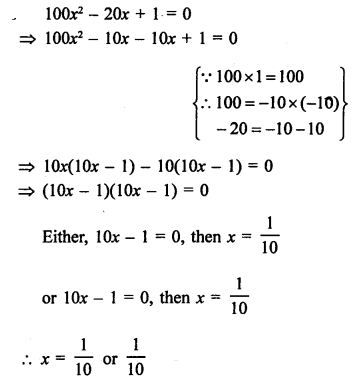
Question 36.
Solution:
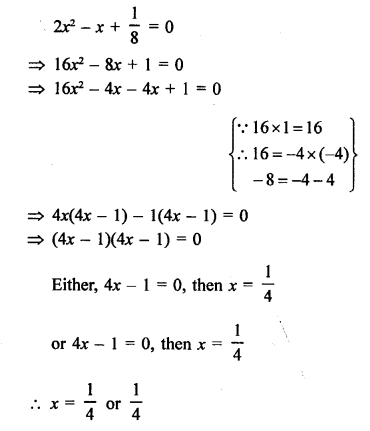
Question 37.
Solution:
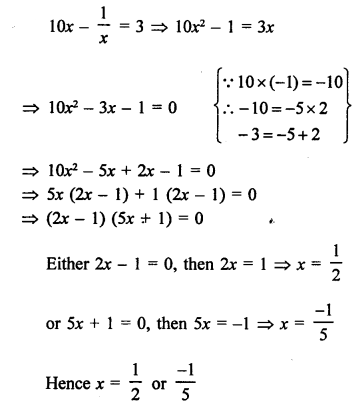
Question 38.
Solution:
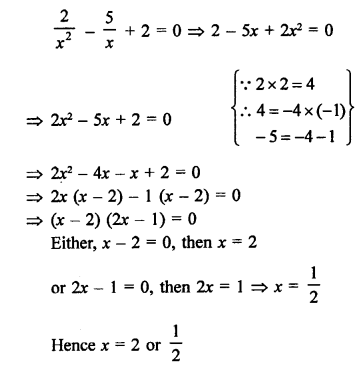
Question 39.
Solution:
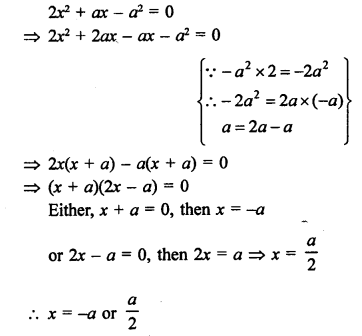
Question 40.
Solution:
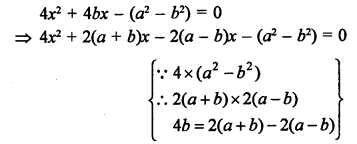
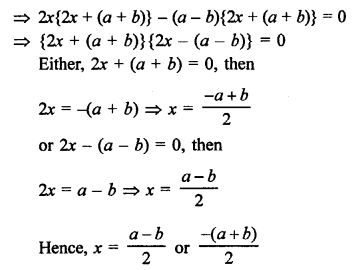
Question 41.
Solution:
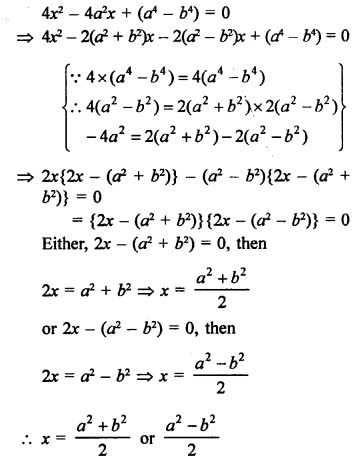
Question 42.
Solution:
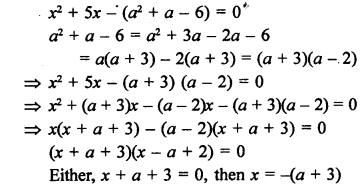
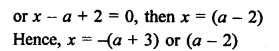
Question 43.
Solution:
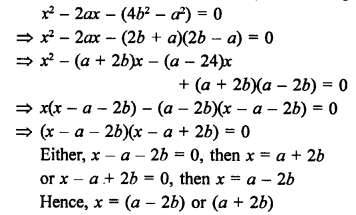
Question 44.
Solution:
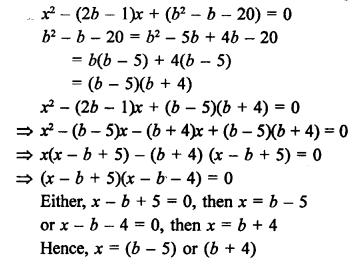
Question 45.
Solution:
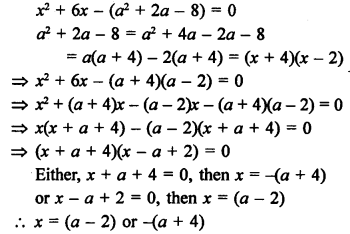
Question 46.
Solution:
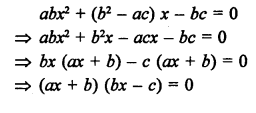
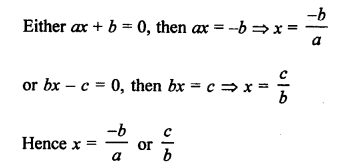
Question 47.
Solution:
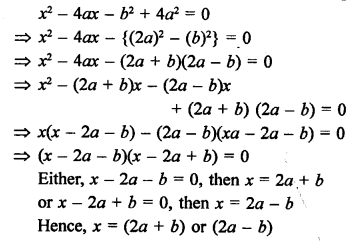
Question 48.
Solution:
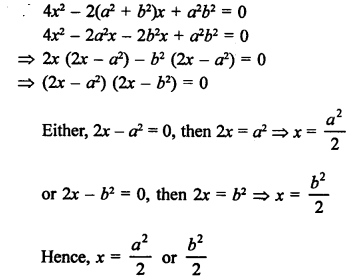
Question 49.
Solution:
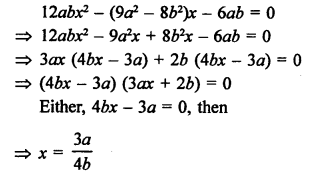
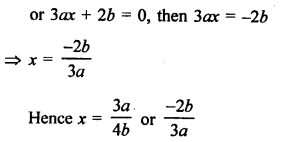
Question 50.
Solution:
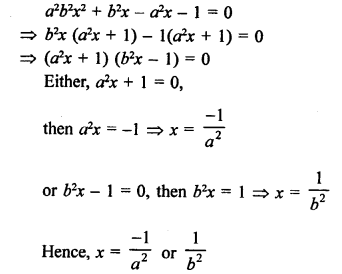
Question 51.
Solution:
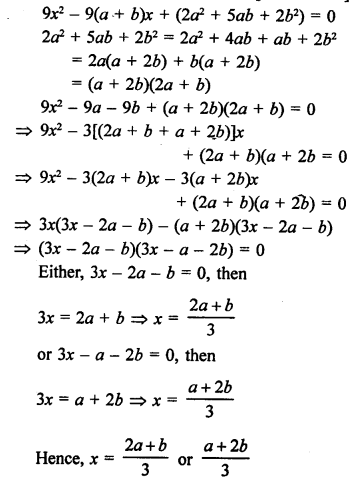
Question 52.
Solution:
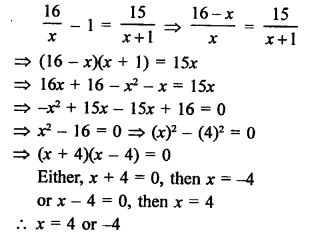
Question 53.
Solution:
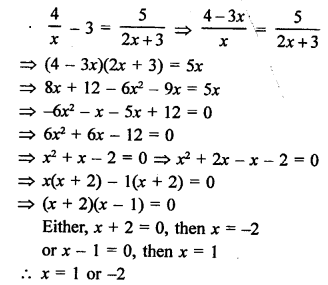
Question 54.
Solution:
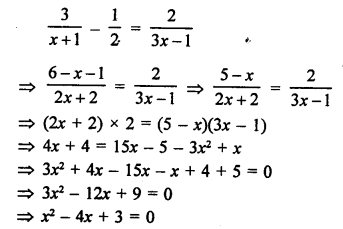
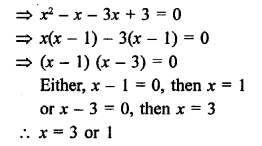
Question 55.
Solution:
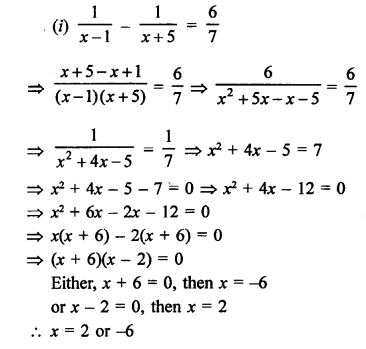
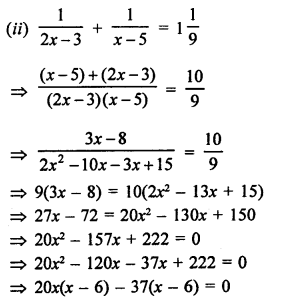
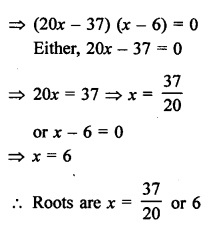
Question 56.
Solution:
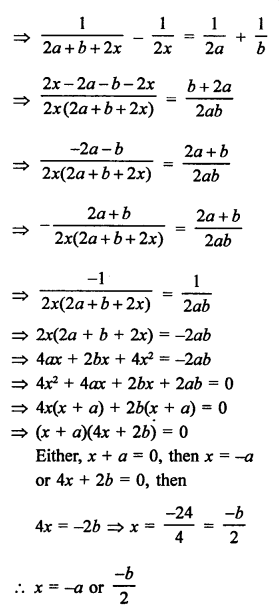
Question 57.
Solution:
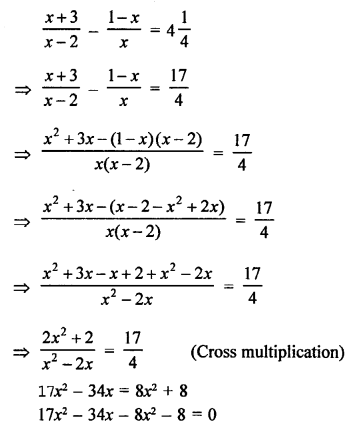
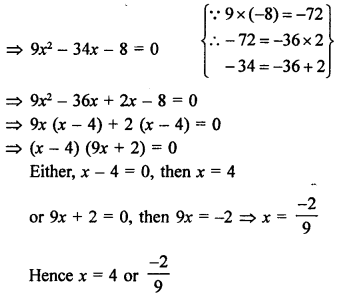
Question 58.
Solution:
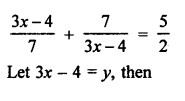
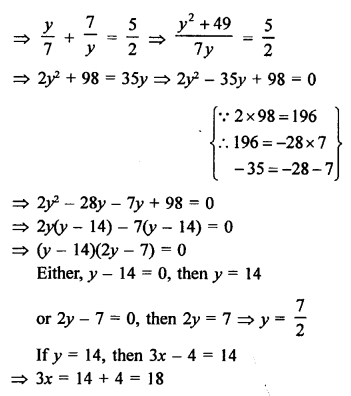
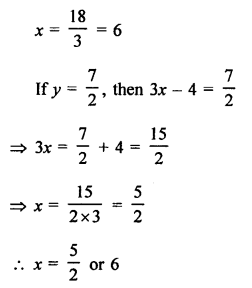
Question 59.
Solution:
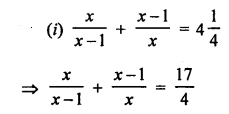
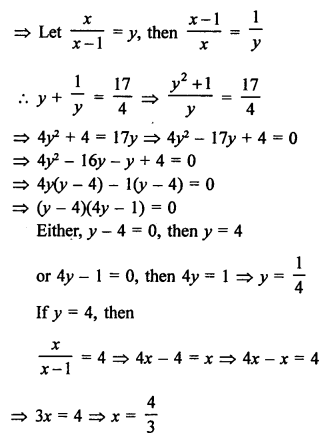
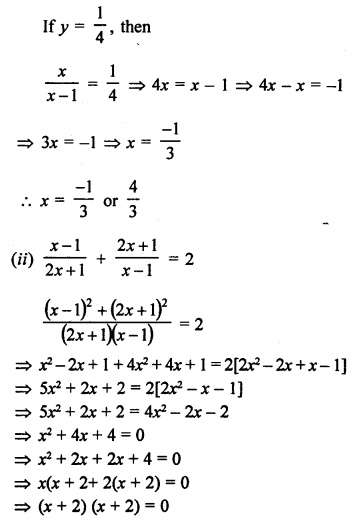
⇒ x = -2
Roots, x = -2
Question 60.
Solution:
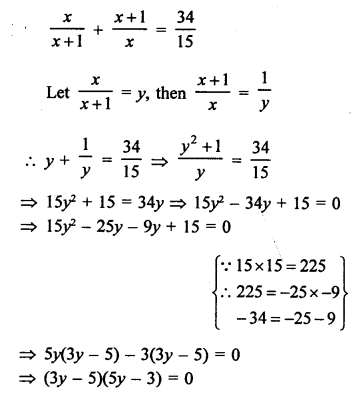
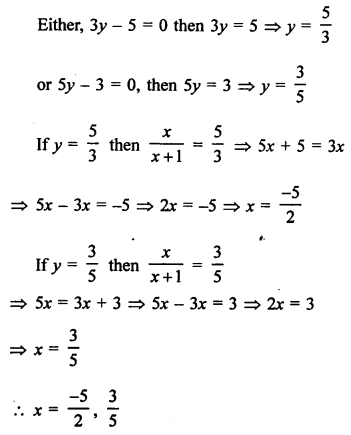
Question 61.
Solution:
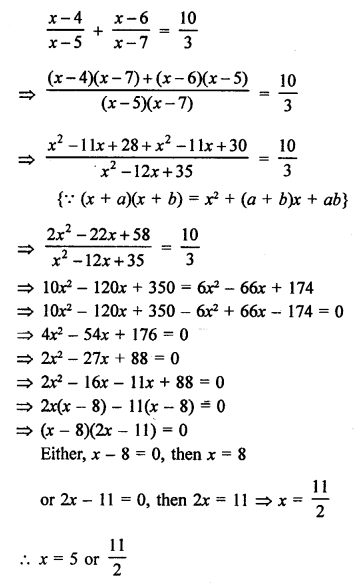
Question 62.
Solution:
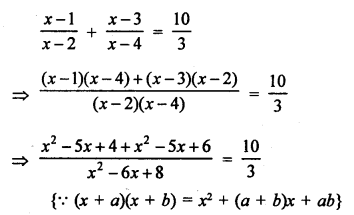
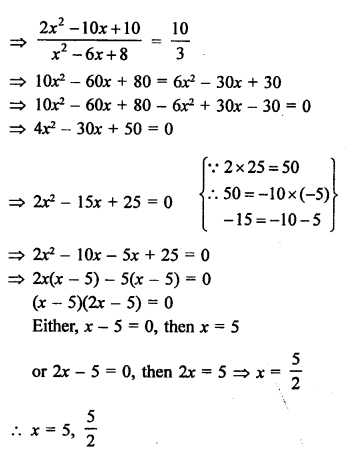
Question 63.
Solution:
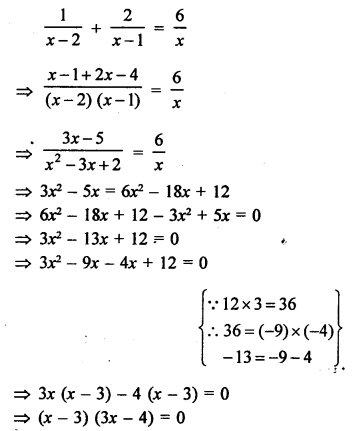
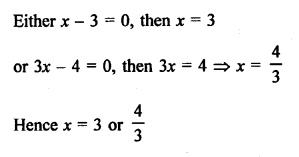
Question 64.
Solution:
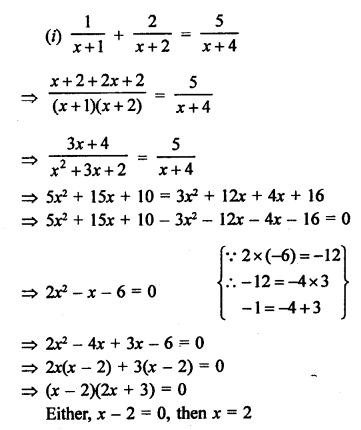
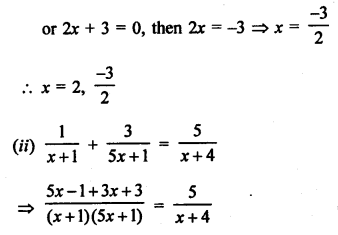
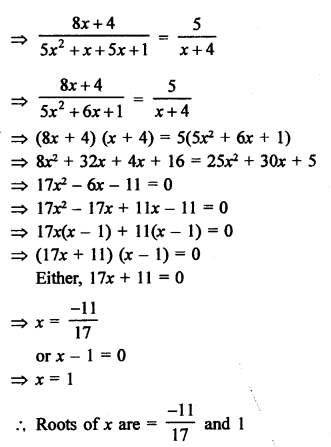
Question 65.
Solution:
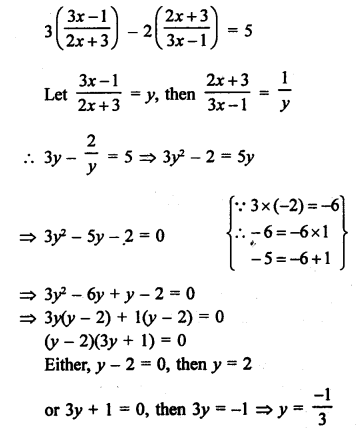
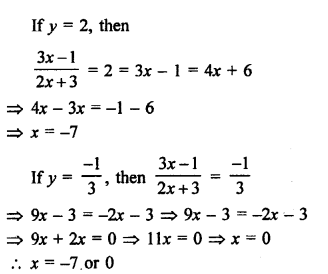
Question 66.
Solution:
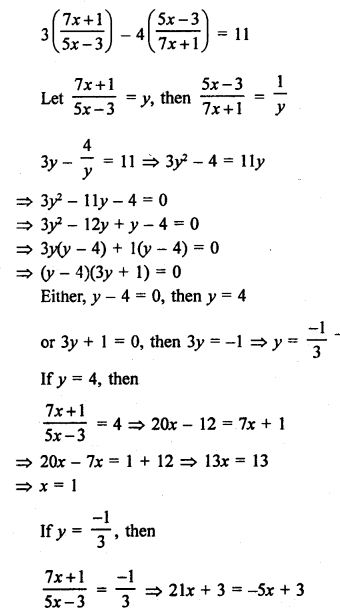
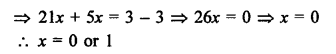
Question 67.
Solution:
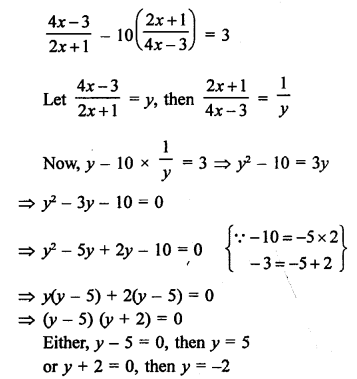
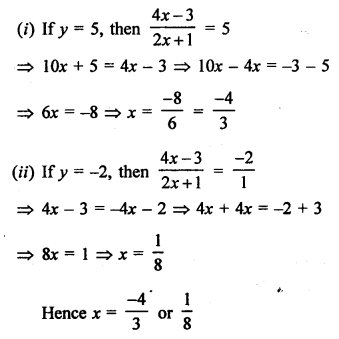
Question 68.
Solution:
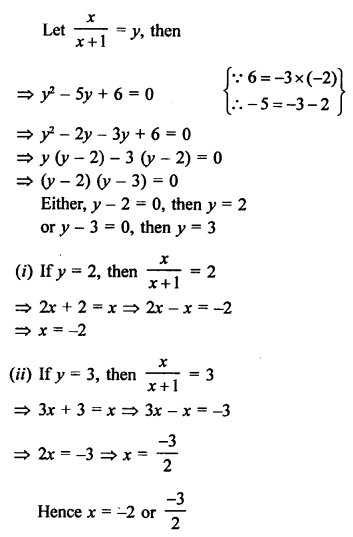
Question 69.
Solution:
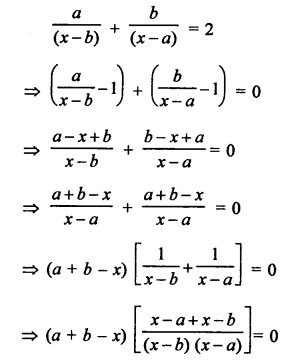
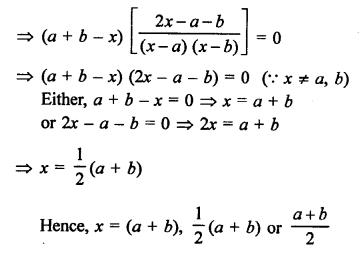
Question 70.
Solution:
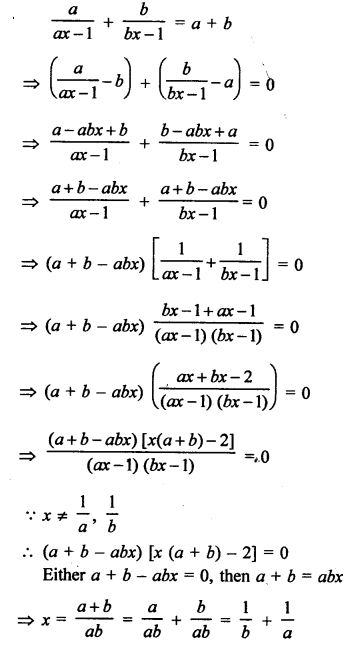
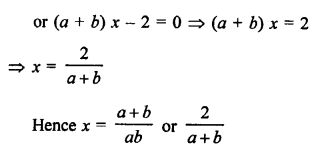
Question 71.
Solution:
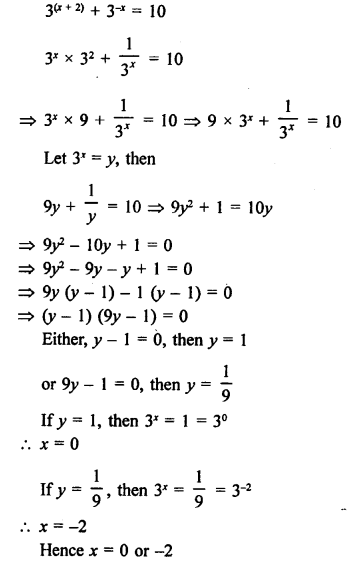
Question 72.
Solution:
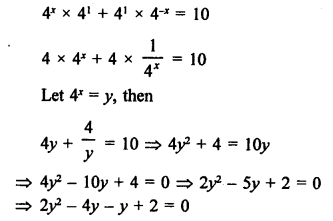
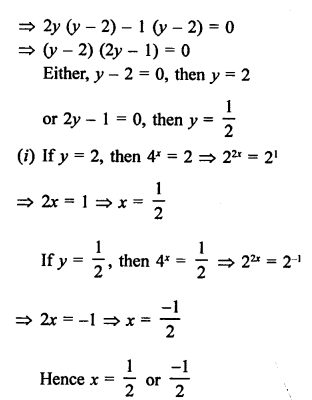
Question 73.
Solution:
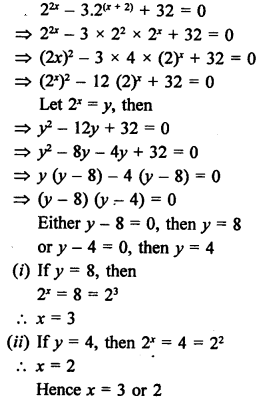
Hope given RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10A are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.