RS Aggarwal Class 10 Solutions Chapter 12 Circles Test Yourself
These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 12 Circles Test Yourself.
Other Exercises
- RS Aggarwal Solutions Class 10 Chapter 12 Circles Ex 12A
- RS Aggarwal Solutions Class 10 Chapter 12 Circles Ex 12B
- RS Aggarwal Solutions Class 10 Chapter 12 Circles MCQS
- RS Aggarwal Solutions Class 10 Chapter 12 Circles Test Yourself
MCQ
Question 1.
Solution:
In the given figure,
PT is the tangent and PQ is the chord of the circle with centre O.
∠OPT = 50°
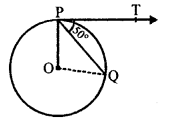
OP is radius and PT is the tangent.
OP ⊥ PT ⇒ ∠OPT = 90°
∠OPQ + ∠QPT = 90°
⇒ ∠OPQ + 50° = 90°
⇒ ∠OPQ = 90° – 50° = 40°
In ∆OPQ,
OP = OQ (radii of the same circle)
∠OQP = ∠OPQ = 40°
In ∆OPQ,
∠POQ = 180° – (∠OPQ + ∠OQP)
= 180° – (40° + 40°) = 180° – 80°
= 100° (b)
Question 2.
Solution:
Angle between two radii of a circle = 130°
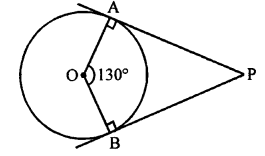
Then ∠APB = 180° – ∠AOB
= 180°- 130° = 50° (c)
Question 3.
Solution:
In the given figure,
PA and PB are the tangents drawn from P to the circle with centre O
∠APB = 80°
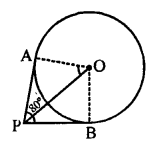
OA is radius of the circle and AP is the tangent
OA ⊥ AP ⇒ ∠OAP = 90°
OP bisects ∠APB,
∠APO = \(\frac { 1 }{ 2 }\) x 80 = 40°
∠POA = 180° – (90° + 40°)
= 180° – 130° = 50° (b)
Question 4.
Solution:
In the given figure, AD and AE are tangents to the circle with centre O.
BC is the tangent at F which meets AD at C and AE at B
AE = 5 cm
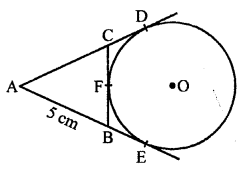
AE and AD are the tangents to the circle
AE = AD = 5 cm
Tangents from an external point drawn to the circle are equal
CD = CF and BE = BF
Now, perimeter of ∆ABC = AB + AC + BC
= AB + AC + BF + CF (BE = BF and CF = CD)
= AB + AC + BE + CD
= AB + BE + AC + CD
= AE + AD
= 5 + 5 = 10 cm (b)
Short-Answer Questions
Question 5.
Solution:
In the given figure, a quadrilateral ABCD is circumscribed a circle touching its sides at P, Q, R and S respectively.
AB = x cm, BC = 7 cm, CR = 3 cm and AS = 5 cm
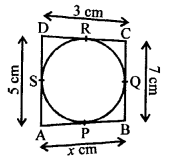
A circle touches the sides of a quadrilateral ABCD.
AB + CD = BC + AD …(i)
Now, AP and AS are tangents to the circle
AP = AS = 5 cm …(ii)
Similarly, CQ = CR = 3 cm
BP = BQ = x – 5 = 4
BQ = BC – CQ = 7 – 3 = 4 cm
x – 5 = 4
⇒ x = 4 + 5 = 9cm
Question 6.
Solution:
In the given figure, PA and PB are the tangents drawn from P to the circle.
OA and OB are the radii of the circle and AP and BP are the tangents.
OA ⊥ AP and OB ⊥ BP
∠OAP = ∠OBP = 90°
In quad. AOBP
∠A + ∠B = 90° + 90° = 180°
But these are opposite angles of a quadrilateral
AOBP is a cyclic quadrilateral
A, O, B, P are concyclic
Question 7.
Solution:
In the given figure, PA and PB are two tangents to the circle with centre O from an external point P.
∠PBA = 65°,
To find : ∠OAB and ∠APB
In ∆APB
AP = BP (Tangents from P to the circle)
∠PAB = ∠PBA = 65°
∠APB = 180° – (∠PAB + ∠PBA)
= 180° – (65° + 65°) = 180° – 130° = 50°
OA is radius and AP is tangent
OA ⊥ AP
∠OAP = 90°
∠OAB = ∠OAP – ∠PAB = 90° – 65° = 25°
Hence, ∠OAB = 25° and ∠APB = 50°
Question 8.
Solution:
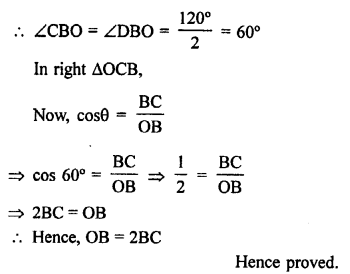
Given : In the figure,
BC and BD are the tangents drawn from B
to the circle with centre O.
∠CBD = 120°
To prove : OB = 2BC
Construction : Join OB.
Proof: OB bisects ∠CBD (OC = OD and BC = BD)
Question 9.
Solution:
(i) A line intersecting a circle in two distinct points is called a secant.
(ii) A circle can have two parallel tangents at the most.
(iii) The common point of a tangent to a circle and the circle is called the point of contact.
(iv) A circle can have infinitely many tangents.
Question 10.
Solution:
Given : In a circle, from an external point P, PA and PB are the tangents drawn to the circle with centre O.
To prove : PA = PB
Construction : Join OA, OB and OP.
Proof : OA and OB are the radii of the circle and AP and BP are tangents.
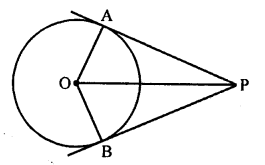
OA ⊥ AP and OB ⊥ BP
⇒ ∠OAP = ∠OBP = 90°
Now, in right ∆OAP and ∆OBP,
Hyp. OP = OP (common)
Side OA = OB (radii of the same circle)
∆OAP = ∆OBP (RHS axiom)
PA = PB (c.p.c.t.)
Hence proved.
Short-Answer Questions
Question 11.
Solution:
Given : In a circle with centre O and AB is its diameter.
From A and B, PQ and RS are the tangents drawn to the circle
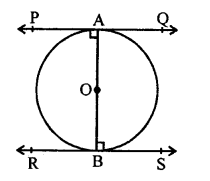
To prove : PQ || RS
Proof : OA is radius and PAQ is the tangent
OA ⊥ PQ
∠PAO = 90° …(i)
Similarly, OB is the radius and RBS is tangent
∠OBS = 90° …(ii)
From (i) and (ii)
∠PAO = ∠OBS
But there are alternate angles
PQ || RS
Question 12.
Solution:
Given : In the given figure,
In ∆ABC,
AB = AC.
A circle is inscribed the triangle which touches it at D, E and F
To prove : BE = CE
Proof: AD and AF are the tangents drawn from A to the circle
AD = AF
But, AB = AC
AB – AD = AC -AF
⇒ BD = CF
But BD = BE and CF = CE (tangent drawn to the circle)
But BD = CF
BE = CE
Hence proved.
Question 13.
Solution:
Given : In a circle from an external point P, PA and PB are the tangents to the circle
OP, OA and OB are joined.
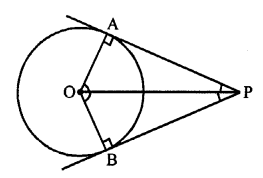
To prove: ∠POA = ∠POB
Proof: OA and OB are the radii of the circle and PA and PB are the tangents to the circle
OA ⊥ AP and OB ⊥ BP
∠OAP = ∠OBP = 90°
Now, in right ∆OAP and ∆OBP,
Hyp. OP = OP (common)
Side OA = OB (radii of the same circle)
∆OAP = ∆OBP (RHS axiom)
∠POA = ∠POB (c.p.c.t.)
Hence proved.
Question 14.
Solution:
Given : A circle with centre O, PA and PB are the tangents drawn from A and B which meets at P.
AB is chord of the circle
To prove : ∠PAB = ∠PBA
Construction : Join OA, OB and OP
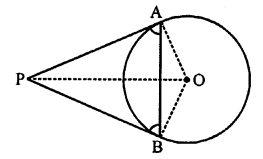
Proof: OA is radius and AP is tangent
OA ⊥ AP ⇒ ∠OAP = 90°
Similarly, OB ⊥ BP ⇒ ∠OBP = 90°
In ∆OAB, OA = OB (radii of the circle)
∠OAB = ∠OBA
⇒ ∠OAP – ∠OAB = ∠OBP – ∠OBA
⇒ ∠PAB = ∠PBA
Hence proved.
Question 15.
Solution:
Given : A parallelogram ABCD is circumscribed a circle.
To prove : ABCD is a rhombus.
Proof: In a parallelogram ABCD.
Opposite sides are equal and parallel.
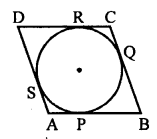
AB = CD and AD = BC
Tangents drawn from an external point of a circle to the circle are equal.
AP = AS BP = BQ
CQ = CR and DR = DS
Adding, we get
AP + BP + CR + DR = AS + BQ + CQ + DS
⇒ (AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
⇒ AB + CD = AD + BC [AB = CD and AD = BC]
⇒ AB + AB = BC + BC
⇒ 2AB = 2BC
⇒ AB = BC
But AB = CD and BC = AD
AB = BC = CD = AD
Hence || gm ABCD is a rhombus.
Question 16.
Solution:
Given : O is the centre of two concentric circles with radii 5 cm and 3 cm respectively.
AB is the chord of the larger circle which touches the smaller circle at P.
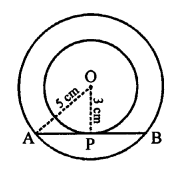
OP and OA are joined.
To find : Length of AB
Proof: OP is the radius of the smaller circle and touches the smaller circle at P
OP ⊥ AB and also bisects AB at P
AP = PB = \(\frac { 1 }{ 2 }\) AB
Now, in right ∆OAP,
OA² = OP² + AP² (Pythagoras Theorem)
⇒ (5)² = (3)² + AP²
⇒ 25 = 9 + AP²
⇒ AP² = 25 – 9 = 16 = (4)²
AP = 4 cm
Hence AB = 2 x AP = 2 x 4 = 8 cm
Long-Answer Questions
Question 17.
Solution:
In the figure, quad. ABCD is circumscribed about a circle which touches its sides at P, Q, R and S respectively
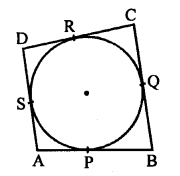
To prove : AB + CD = AD + BC
Proof: Tangents drawn from an external point to a circle are equal
AP = AS
BP = BQ
CR = CQ
DR = DS
Adding, we get,
AP + BP + CR + DR = AS + BQ + CQ + DS
⇒ (AP + BP) + (CR + DR) = (AS + DS) + (BQ + CQ)
⇒ AB + CD = AD + BC
Hence AB + CD = AD + BC
Question 18.
Solution:
Given : A quad. ABCD circumscribe a circle with centre O and touches at P, Q, R and S respectively
OA, OB, OC and OD are joined forming angles AOB, BOC, COD and DOA
To prove : ∠AOB + ∠COD = 180°
and ∠BOC + ∠AOD = 180°
Construction : Join OP, OQ, OR and OS
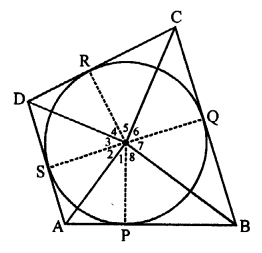
Proof: In right ∆AOP and ∆AOS,
Side OP = OS (radii of the same circle)
Hyp. OA = OA (common)
∆AOP = ∆AOS (RHS axiom)
∠1 = ∠2 (c.p.c.t.)
Similarly, we can prove that
∠4 = ∠3
∠5 = ∠6
∠8 = ∠7
Adding, we get
∠1 + ∠4 + ∠5 + ∠8 = ∠2 + ∠3 + ∠6 + ∠7
⇒ (∠1 + ∠8) + (∠4 + ∠5) = (∠2 + ∠3) + (∠6 + ∠7)
⇒ ∠AOB + ∠COD = ∠AOD + ∠BOC
But ∠AOB + ∠BOC + ∠COD + ∠DOA = 360° (angles at a point)
∠AOB + ∠COD = ∠AOD + ∠BOC = 180°
Hence proved
Question 19.
Solution:
Given : From an external point P, PA and PB are the tangents drawn to the circle,
OA and OB are joined.
To prove : ∠APB + ∠AOB = 180°
Construction : Join OP.
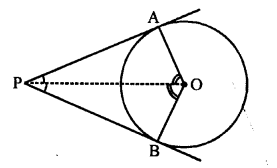
Proof : Now, in ∆POA and ∆PBO,
OP = OP (common)
PA = PB (Tangents from P to the circle)
OA = OB (Radii of the same circle)
∆POA = ∆PBO (SSS axiom)
∠APO = ∠BPO (c.p.c.t.)
and ∠AOP = ∠BOP (c.p.c.t.)
OA and OB are the radii and PA and PB are the tangents
OA ⊥ AP and OB ⊥ BP
⇒ ∠OAP = 90° and ∠OBP = 90°
In ∆POA,
∠OAP = 90°
∠APO + ∠AOP = 90°
Similarly, ∠BPO + ∠BOP = 90°
Adding, we get
(∠APO + ∠BPO) + (∠AOP + ∠BOP) = 90° + 90°
⇒ ∠APB + ∠AOB = 180°.
Hence proved.
Question 20.
Solution:
Given : PQ is chord of a circle with centre O.
TP and TQ are tangents to the circle
Radius of the circle = 10 cm
i.e. OP = OQ = 10 cm and PQ = 16 cm
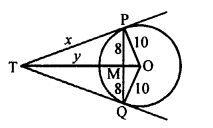
To find : The length of TP.
OT bisects the chord PQ at M at right angle.
PM = MQ = \(\frac { 16 }{ 2 }\) = 8 cm
In right ∆PMO,
OP² = PM² + MO² (Pythagoras Theorem)
⇒ (10)² = (8)² + MO²
⇒ 100 = 64 + MO²
⇒ MO² = 100 – 64 = 36 = (6)²
MO = 6 cm
Let TP = x and TM = y
In right ∆TPM,
TP² = TM² + PM²
⇒ x² = y² + 8²
⇒ x² = y² + 64 …(i)
and in right ∆TPM
OT² = TP² + OP²
⇒ (y + 6)² = x² + 10²
⇒ y² + 12y + 36 = x² + 100
⇒ y² + 12y + 36 = y2 + 64 + 100 {From (i)}
⇒ 12y = 64 + 100 – 36 = 128
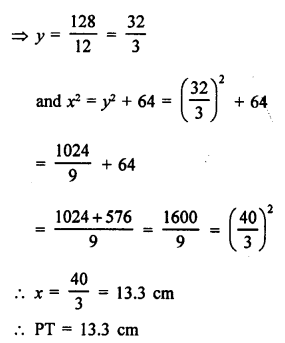
Hope given RS Aggarwal Solutions Class 10 Chapter 12 Circles Test Yourself are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.