RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12B

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 12 Circles Ex 12B.

Other Exercises

Very-Short-Answer Questions
Question 1.
Solution:
In the given figure, a circle touches the sides AB, BC, CD and DA of a quadrilateral ABCD at P, Q, R and S respectively.
AB = 6 cm, BC = 9 cm, CD = 8 cm.
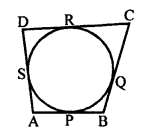
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12B 1
To find : The length of side AD.
A circle touches the sides of a quadrilateral ABCD.
AB + CD = BC + AD
=> 6 + 8 = 9 + AD
=> 14 = 9 + AD
=> AD = 14 – 9 = 5 cm

Question 2.
Solution:
In the given figure, PA and PB are two tangents to the circle with centre O.
∠APB = 50°
To find : Measure of ∠OAB.
Construction : Join OB.
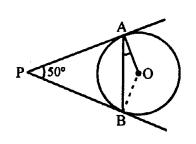
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12B 2
In ∆APB,
PA = PB (tangents of the circle)
∠PAB = ∠PBA
But, ∠PAB + ∠PBA + ∠APB = 180° (Angles of a triangle)
=> ∠PAB + ∠PAB + 50° = 180°
=> 2∠PAB = 180° – 50° = 130°
∠PAB = 65°
But ∠OAP = 90° (OA is radius and PA is tangent)
∠OAB = 90° – 65° = 25°

Question 3.
Solution:
In the given figure, O is the centre of a circle.
PT and PQ are tangents to the circle from an external point P.
R is any point on the circle. RT and RQ are joined.
∠TPQ = 70°
To find : ∠TRQ
Construction : Join TO and QO.
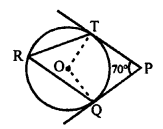
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12B 3
∠TPQ = 70°
∠TOQ = 180° – 70° = 110° (OT and OQ are perpendicular on TP and QP)
Now, ∠TOQ is on the centre and ∠TRQ is on the remaining part of the circle.
∠TRQ = \(\frac { 1 }{ 2 }\) x ∠TOQ = \(\frac { 1 }{ 2 }\) x 110° = 55°

Question 4.
Solution:
In the given figure, common tangents AB and CD to the two circles with centres O1 and O2 intersect each other at E.
To prove : AB = CD.
Proof : EA and EC are tangents to the circle O1
EA = EC …(i)
Similarly, EB and ED are tangents to the circle O2.
EB = ED …(ii)
Adding (i) and (ii),
EA + EB = EC + ED
=> AB = CD
Hence, AB = CD

Question 5.
Solution:
In the given figure, PT is the tangent to the circle with centre O at P.
PQ is a chord of the circle and ∠TPQ = 70°.
To find : The measure of ∠POQ.
PT is tangent and OP is the radius.
∠OPT = 90°
But ∠QPT = 70°
∠OPQ = 90° – 70° = 20°
In ∆OPQ,
OP = OQ (radii of the same circle)
∠OQP = ∠OPQ = 20°
and ∠POQ = 180° – (∠OPQ + ∠OQP)
= 180° – (20° + 20°)
= 180° – 40° = 140°

Short-Answer Questions
Question 6.
Solution:
In the given figure, ∆ABC is circumscribed a circle with centre O and radius 2 cm.
Point D divides BC in such a way that
BD = 4 cm, DC = 3 cm, OD = 2 cm
Area of ∆ABC = 21 cm²
To find : AB and AC.
Construction : Join OA, OB, OC, OE and OF.
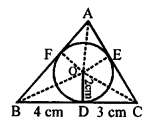
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12B 4
BD and BF are tangents to the circle.
BF = BD = 4 cm.
Similarly, CD and CE are tangents.
CE = CD = 3 cm
and AF and AE are tangents
AE = AF = x (suppose)
Now, area of ∆ABC = \(\frac { 1 }{ 2 }\) x Perimeter of ∆ABC x Radius
21 = \(\frac { 1 }{ 2 }\) (AB + BC + CA) x OD
=> 21 x 2 = [4 + 3 + 3+ x + x + 4) x 2
=> 42 = (14 + 2x) x 2
=> 14 + 2x = \(\frac { 42 }{ 2 }\) = 21
=> 2x = 21 – 14 = 7
x = \(\frac { 7 }{ 2 }\) = 3.5
AB = AF + FB = 3.5 + 4 = 7.5 cm
AC = AE + CE = 3.5 + 3 = 6.5 cm

Question 7.
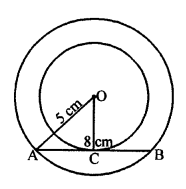
Solution:
Given : Two concentric circles with centre O and radii 5 cm and 3 cm respectively.
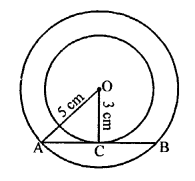
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12B 5
AB is chord of larger circle which touches the smaller circle at C.
To find : The length of chord AB.
Construction : Join OA and OC.
AB is tangent and OC is radius of the smaller circle.
OC ⊥ AB and OC bisects AB at C. (AB is chord and OC ⊥ AB)
In right ∆OAC,
OA² = OC² + AC² (Pythagoras Theorem)
=> (5)² = (3)² + AC²
=> 25 = 9 + AC²
=> AC² = 25 – 9 = 16 = (4)²
=> AC = 4
and AB = 2 x AC = 2 x 4 = 8cm

Question 8.
Solution:
Given : AB is the tangent to the circle with centre O at point P.
PL ⊥ AB
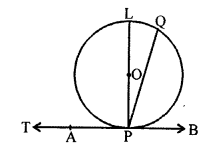
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12B 6
To prove : PL passes through O.
Let PQ ⊥PT where Q lies on the circle.
∠QPT = 90°
Let PQ does not pass through the centre O.
Join PO and produce it to meet the circle at L.
PO being the radius of the circle drawn from the point of contact P.
OP ⊥ AB
=> ∠OPB = 90° => ∠LPB = 90°
But, PQ ⊥ AB
∠QPB = 90°
It is possible only if L and Q coincide each other.
Hence, PQ passes through the centre and is perpendicular from the point of contact.

Question 9.
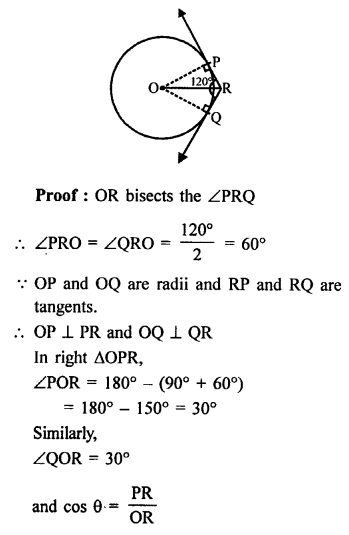
Solution:
In the given figure, two tangents RQ and RP are drawn from the external point R to the circle with centre O.
∠PRQ = 120°
To prove : OR = PR + RQ
Construction : Join OP and OQ.
Also join OR.
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12B 7
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12B 8

Question 10.
Solution:
In the given figure, a circle is inscribed in a ∆ABC touches the sides AB, BC and CA at D, E and F respectively.
AB = 14 cm, BC = 8 cm and CA = 12 cm.
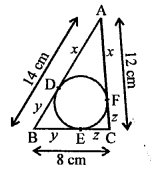
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12B 9
To find : The length of AD, BE and CF.
Let AD = x, BE = y and CF = z
AD and AF are the tangents to the circle from A.
AD = AF = x
Similarly,
BE and BD are tangents
BD = BE = y
and CF and CE are the tangents
CE = CF = z
Now, AB + BC + CA = 14 + 8 + 12 = 34
=> (x + y) + (y + z) + (z + x) = 34
=> 2 (x + y + z) = 34
=> x + y + z = 17 …(i)
But x + y = 14 cm …(ii)
y + z = 8 cm …(iii)
z + x = 12 cm …(iv)
Subtracting (iii), (iv) and (ii) from (i) term by term
x = 17 – 8 = 9 cm
y = 17 – 12 = 5 cm
z = 17 – 14 = 3 cm
Hence, AD = 9 cm, BE = 5 cm and CF = 3 cm.

Question 11.
Solution:
In the given figure, O is the centre of the circle.
PA and PB are the tangents.
To prove : AOBP is a cyclic quadrilateral.
Proof: OA is radius and PA is tangent
OA ⊥ PA
=> ∠OAP = 90° ….. (i)
Similarly, OB is radius and PB is tangent.
OB ⊥ PB
=> ∠OBP = 90° ….. (ii)
Adding (i) and (ii),
∠OAP + ∠OBP = 90° + 90° = 180°
But these are opposite angles of the quadrilateral AOBP.
Quadrilateral AOBP is a cyclic.

Question 12.
Solution:
In two concentric circles with centre O, a chord AB of the laiger circle touches the smaller circle at C.
AB = 8 cm and radius of larger circle = 5 cm
Join OA, OC
To find, the radius of smaller circle,
AB is the tangent and OC is the radius
OC ⊥ AB
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12B 10
AC = CB = \(\frac { 8 }{ 2 }\) = 4 cm
OA = 5 cm
In right ∆OCA,
OA² = OC² + AC² (Pythagoras Theorem)
(5)² = OC² + (4)²
OC² = (5)² – (4)² = 25 – 16 = 9 = (3)²
OC = 3
Radius of smaller circle = 3 cm

Question 13.
Solution:
In the given figure, PQ is a chord of a circle with centre O.
PT is the tangent ∠QPT = 60°.
To find : ∠PRQ.
Construction : Take a point M on the alternate segment.
Join MP and MQ.
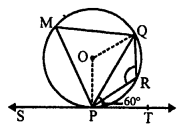
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12B 11
∠MPQ = ∠QPT = 60° (Angles in the alternate segment)
∠PMQ + ∠PRQ = 180° (Opposite angles of a cyclic quadrilateral)
=> 60° + ∠PRQ = 180°
∠PRQ = 180° – 60° = 120°
Hence, ∠PRQ = 120°

Question 14.
Solution:
In the given figure,
PA and PB are the two tangents to the circle.
With centre O, OA and AB are joined
∠APB = 60°
To find : The measure of ∠OAB
PA and PB are tangents to the circle from P
PA = PB
∠PAB = ∠PBA
But ∠APB = 60°
∠PAB + ∠PBA = 180° – 60° = 120°
2 ∠PAB = 120°
∠PBA = 60°
OA is radius and PA is tangent.
OA ⊥ PA
∠OAP = 90°
=> ∠OAB + ∠PAB = 90°
=> ∠OAB + 60° = 90°
=> ∠OAB = 90° – 60° = 30°
Hence, ∠OAB = 30°

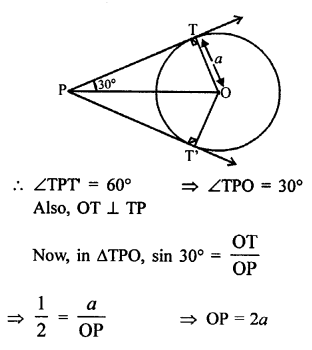
Question 15.
Solution:
Since, tangents drawn from an external point are equally inclined to the line joining centre to that point.
RS Aggarwal Class 10 Solutions Chapter 12 Circles Ex 12B 12

Hope given RS Aggarwal Solutions Class 10 Chapter 12 Circles Ex 12B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.