RS Aggarwal Class 10 Solutions Chapter 10 Quadratic Equations Ex 10E

RS Aggarwal Class 10 Solutions Chapter 10 Quadratic Equations Ex 10E

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10E.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10A
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10B
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10C
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10D
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10E
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Test Yourself

PROBLEMS ON NUMBERS
Question 1.
Solution:
Let natural number be = x
According to the condition,
x² + x = 156
⇒ x² + x – 156 = 0
⇒ x² + 13x – 12x – 156 = 0
⇒ x (x + 13) – 12 (x + 13) = 0
⇒ (x + 13) (x – 12) = 0
Either, x + 13 = 0, then x = -13 but it is not a natural number
or x – 12 = 0, then x = 12
Hence, required number = 12

Question 2.
Solution:
Let the natural number be x,
Then according to the condition,
x + √x = 132
Let √x = y, then
y² + y = 132
⇒ y² + y – 132 = 0
⇒ y² + 12y – 11y – 132 = 0
⇒ y (y + 12) – 11 (y + 12) = 0
⇒ (y + 12) (y – 11) = 0
Either, y + 12 = 0, then y = -12 but it is not a natural number.
or y – 11 = 0 ⇒ y = 11
√x = 11 ⇒ x = 121
Hence, required number =121

Question 3.
Solution:
Sum of two natural numbers = 28
Let first number = x
Then second number = 28 – x
According to the condition,
x (28 – x) = 192
⇒ 28x – x² = 192
⇒ x² – 28x + 192 = 0
⇒ x² – 16x – 12x + 192 = 0
⇒ x (x – 16) – 12 (x – 16) = 0
⇒ (x – 16)(x – 12) = 0
Either, x – 16 = 0, then x = 16
or x – 12 = 0, then x = 12
Required natural numbers are 16 and 12

Question 4.
Solution:
Let first integer = x
Then second = x + 1
According to the condition,
(x)² + (x + 1)² = 365
⇒ x² + x² + 2x + 1 = 365
⇒ 2x² + 2x + 1 – 365 = 0
⇒ 2x² + 2x – 364 = 0
⇒ x² + x – 182 = 0
⇒ x² + 14x – 13x – 182 = 0
⇒ x(x + 14) – 13(x + 14) = 0
⇒ (x + 14)(x – 13) = 0
Either, x + 14 = 0, then x = -14 but it is negative.
or x – 13 = 0, then x = 13
First number = 13
and second number = 13 + 1 = 14
Hence, the numbers are 13, 14

Question 5.
Solution:
Let first odd number = x
Then second consecutive odd number = x + 2
According to the condition,
x² + (x + 2)² = 514
⇒x² + x² + 4x + 4 = 514
⇒ 2x² + 4x + 4 – 514 = 0
⇒ 2x² + 4x – 510 = 0
⇒ x² + 2x – 255 = 0
⇒ x² + 17x – 15x – 255 = 0
⇒ x (x + 17) – 15 (x + 17) = 0
⇒ (x + 17) (x – 15) = 0
Either, x + 17 = 0, then x = -17 but it is not positive.
or x – 13 = 0, then x = 13
First odd number = 13
and second number = 13 + 2 = 15
Hence, the number are 15, 17

Question 6.
Solution:
Let first positive even number = x
Then second even number = x + 2
According to the condition, x² + (x + 2)² = 452
⇒ x² + x² + 4x + 4 = 452
⇒ 2x² + 4x + 4 – 452 = 0
⇒ 2x² + 4x – 448 = 0
⇒ x² + 2x – 224 = 0
⇒ x² + 16x – 14x – 224 = 0
⇒ x (x + 16) – 14 (x + 16) = 0
⇒ (x + 16) (x – 14) = 0
Either, x + 16 = 0, then x = 16 which is not positive.
or x – 14 = 0, then x = 14
First even number = 14
and second number = 14 + 2 = 16
Hence, the numbers are 14, 16

Question 7.
Solution:
Let first positive integer = x
Then second integer = x + 1
According to the condition,
x (x + 1) = 306
⇒ x² + x – 306 = 0
⇒ x² + 18x – 17x – 306 = 0
⇒ x (x + 18) – 17 (x + 18) = 0
⇒ (x + 18)(x – 17) = 0
Either, x + 18 = 0, then x = -18 which is not positive.
or x – 17 = 0, then x = 17
First number =17
and second integer = 17 + 1 = 18
Hence, the numbers are 17, 18

Question 8.
Solution:
Let first natural number = x
Then second number = x + 3
According to the condition,
x (x + 3) = 504
⇒ x² + 3x – 504 = 0
⇒ x² + 24x – 21x – 504 = 0
⇒ x(x + 24) – 21(x + 24) = 0
⇒ (x + 24)(x – 21) = 0
Either x + 24 = 0, then x = -24 but it is not positive.
or x – 21 =0, then x = 21
First natural number = 21
and second number = 21 + 3 = 24
Hence, two required numbers are 21, 24

Question 9.
Solution:
Let first multiple of 3 = 3x
and second = 3x + 3
According to the condition,
3x (3x + 3) = 648
⇒ 9x² + 9x – 648 = 0
⇒ x² + x – 72 = 0
⇒ x² + 9x – 8x – 72 = 0
⇒ x (x + 9) – 8 (x + 9) = 0
⇒ (x + 9)(x – 8) = 0
Either, x + 9 = 0, then x = -9 which is negative.
or x – 8 = 0, then x = 8
First multiple of 3 = 3 x 8 = 24
and second = 24 + 3 = 27
Hence, numbers are 24, 27

Question 10.
Solution:
Let first positive odd integer = x
Then second = x + 2
According to the condition,
x (x + 2) = 483
⇒ x² + 2x – 483 = 0
⇒ x² + 23x – 21x – 483 = 0
⇒ x (x + 23) – 21(x + 23) = 0
⇒ (x + 23)(x – 21) = 0
Either, x + 23 = 0, then x = -23 which is negative.
or x – 21 =0, then x = 21
First odd number = 21
and second = 21 + 2 = 23
Hence, numbers are 21, 23

Question 11.
Solution:
Let first positive even integer = 2x
Then second even integer = 2x + 2
According to the condition,
2x (2x + 2) = 288
⇒ 4x² + 4x – 288 = 0
⇒ x² + x – 12 = 0
⇒ x² + 9x – 8x – 72 = 0
⇒ x (x + 9) – 8 (x + 9) = 0
⇒ (x + 9) (x – 8) = 0
Either, x + 9 = 0, then x = -9 which is negative.
or x – 8 = 0, then x = 8
First even integer = 2 x 8 = 16
and second even integer = 16 + 2 = 18
Hence, required integers are 16, 18

Question 12.
Solution:
Sum of two natural numbers = 9
Let first number = x
Then second number = 9 – x
According to the condition,

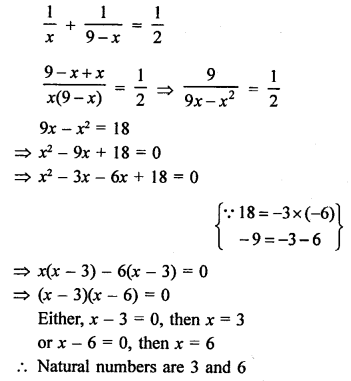
Question 13.
Solution:
Sum of two natural numbers = 15
Let first number = x
Then second number = 15 – x
According to the condition,

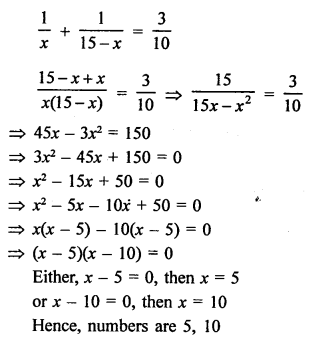
Question 14.
Solution:
Difference of two natural numbers = 3
Let first number = x
Then second number = x + 3
According to the condition,

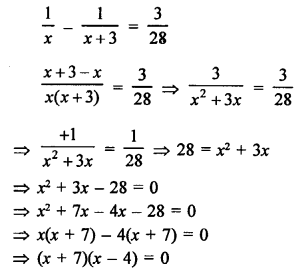
Either, x + 7 = 0, then x = -7 which is negative.
or x – 4 = 0, then x = 4.
First number = 4
and second number = 4 + 3 = 7
Hence, the numbers are 4, 7

Question 15.
Solution:
Difference of two natural numbers = 5
Let first number = x
Then second number = x – 5
According to the condition,

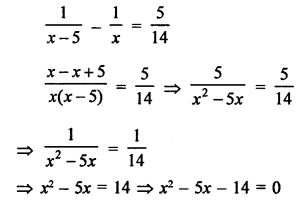
⇒ x (x – 7) + 2 (x – 7) = 0
⇒ (x – 7) (x – 2) = 0
Either, x – 7 = 0, then x = 7
or x + 2 = 0, then x = -2 which is negative
First number = 7
and second number = 7 – 5 = 2
Hence, numbers are 7, 2

Question 16.
Solution:
Let first number = 7x
Then second number = 7x + 7
According to the condition,
(7x)² + (7x + 7)² = 1225
⇒ 49x² + 49x² + 49 + 98x = 1225
⇒ 98x² + 98x + 49 – 1225 = 0
⇒ 98x² + 98x – 1176 = 0
⇒ x² + x – 12 = 0 (Dividing by 98)
⇒ x² + 4x – 3x – 12 = 0
⇒ x (x + 4) – 3 (x + 4) = 0
⇒ (x + 4) (x – 3) = 0
Either, x + 4 = 0, then x = -4 which is negative.
or x – 3 = 0, then x = 3
First number 3 x 7 = 21
and second number = 21 + 7 = 28
Hence, numbers are 21, 28

Question 17.
Solution:
Let the natural number = x
According to the condition,

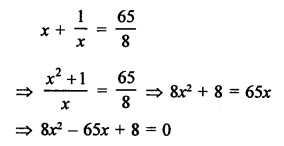
⇒ 8x² – 64x – x + 8 = 0
⇒ 8x (x – 8) – 1 (x – 8) = 0
⇒ (x – 8) (8x – 1) = 0
Either, x – 8 = 0, then x = 8
or 8x – 1 = 0, then 8x = 1 ⇒ x = \(\frac { 1 }{ 8 }\) which is not a natural number.
Required natural number = 8

Question 18.
Solution:
Let first part = x
Then second part = 57 – x
According to the condition,
x (57 – x) = 680
⇒ 57x – x² = 680
⇒ x² – 57x + 680 = 0
⇒ x² – 40x – 17x + 680 = 0
⇒ x (x – 40) – 17 (x – 40) = 0
⇒ (x – 40) (x – 17) = 0
Either, x – 40 = 0, then x = 40
or x – 17 = 0, then x = 17
If first part is 40, then second part = 57 – 40 = 17
Parts are 40, 17 or 17, 40

Question 19.
Solution:
Let first part = x
Then second part = 27 – x
According to the condition,

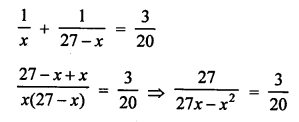
⇒ 81x – 3x² = 540
⇒ 3x² – 81x + 540 = 0
⇒ x² – 27x + 180 = 0
⇒ x² – 12x – 15x + 180 = 0
⇒ x(x – 12) – 15(x – 12) = 0
⇒ (x – 12)(x – 15) = 0
Either, x – 12 = 0, then x = 12
or x – 15 = 0, then x = 15
If first part is 12, then
second part = 27 – 12 = 15
Parts are 12, 15 or 15, 12

Question 20.
Solution:
Let first part (larger) = x
Then second part = 16 – x
According to the condition,
2(x²) – (16 – x)² = 164
⇒ 2x² – (256 + x² – 32x) = 164
⇒ 2x² – 256 – x² + 32x – 164 = 0
⇒ x² + 32x – 420 = 0
⇒ x² + 42x – 10x – 420 = 0
⇒ x (x + 42) – 10 (x + 42) = 0
⇒ (x + 42) (x – 10) = 0
either x + 42 = 0, then x = -42 which is negative.
or x – 10 = 0, then x = 10
First part =10
and second part =16 – 10 = 6
Hence, parts are 10 and 6

Question 21.
Solution:
Let a and b be the two natural numbers.
According to the condition,
a² + b² = 25(a + b) and a² + b² = 50(a – b)
25(a + b) = 50(a – b)
⇒ a + b = 2(a – b)
⇒ a + b = 2a – 2b
⇒ 2a – a = 2b + b
⇒ a = 3b
Now, a² + b² = 25(a + b)
⇒ (3b)² + b² = 25(3b + b)
⇒ 9b² + b² = 25 x 4b
⇒ 10b² = 100b
⇒ b² = 10b
⇒ b² – 10b = 0
⇒ b(b – 10) = 0
Either, b = 0 which is not possible
or b – 10 = 0, then b = 10
a = 3b = 3 x 10 = 30
Numbers are 30 and 10

Question 22.
Solution:
Let the two natural numbers be a and b.
According to the condition,
a² – b² = 45 and b² = 4a
⇒ a² – 4a = 45
⇒ a² – 4a – 45 = 0
⇒ a² – 9a + 5a – 45 = 0
⇒ a(a – 9) + 5 (a – 9) = 0
⇒ (a – 9) (a + 5) = 0
Either, a – 9 = 0, then a = 9
or a + 5 = 0, then a = -5 which is not a natural number.
a = 9
and b² = 4a = 4 x 9 = 36 = (6)²
b = 6
Hence, numbers are 9, 6

Question 23.
Solution:
Let three consecutive positive integers be x, x + 1 and x + 2
According to the condition,
x² + (x + 1) (x + 2) = 46
⇒ x² + x² + 3x + 2 – 46 = 0
⇒ 2x² + 3x – 44 = 0
⇒ 2x² – 8x + 11x – 44 = 0
⇒ 2x (x – 4) + 11 (x – 4) = 0
⇒ (x – 4) (2x + 11) = 0
Either, x – 4 = 0, then x = 4
or 2x + 11 = 0, then 2x = -11 ⇒ x = \(\frac { -11 }{ 2 }\)
But it is not a natural number.
x = 4
Hence, three consecutive numbers are 4, 5, 6.

Question 24.
Solution:
Let the digits of a two digit number be x and y
Let one’s digit = x
and ten’s digit = y
Number = x + 10y
According to the condition,
x + 10y = 4(x + y)
and x + 10y = 2xy
Now, x + 10y = 4x + 4y
⇒ 10y – 4y = 4x – x
⇒ 3x = 6y
⇒ x = 2y …(i)
x + 10y = 2xy
⇒ 2y + 10y = 2 x 2y x y
⇒ 12y = 4y²
⇒ 3y = y²
⇒ y² – 3y = 0
⇒ y (y – 3) = 0
Either, y = 0, which is not possible,
or y – 3 = 0, then y = 3
x = 2y = 2 x 3 = 6
and number = x + 10y = 6 + 10 x 3 = 6 + 30 = 36

Question 25.
Solution:
Let the ones digit of a two digit number = x
and ten’s digit = y
Number = x + 10y
By reversing the digits,
the One’s digit = y
and ten’s digit = x
Number = y + 10x
According to the condition,
x + 10y + 45 = y + 10x
⇒ 10y – y + x – 10x = -45
9y – 9x = -45
⇒ x – y = 5
⇒ x = y + 5
and xy = 14
⇒ (y + 5) x y = 14
⇒ y² + 5y – 14 = 0
⇒ y² + 7y – 2y – 14 = 0
⇒ y (y + 7) – 2(y + 7) = 0
⇒ (y + 7)(y – 2) = 0
Either, y + 7 = 0, then x = -7 which is negative, so not possible.
or y – 2 = 0, then y = 2
x = y + 5 = 2 + 5 = 7
Number = x + 10y = 7 + 10 x 2 = 7 + 20 = 27

Question 26.
Solution:
Let numerator = x
Then denominator = x + 3

⇒ x² + 5x – 2x – 10 = 0
⇒ x (x + 5) – 2 (x + 5) = 0
⇒ (x + 5)(x – 2) = 0
Either x + 5 = 0, then x = -5 which not possible being negative,
or x – 2 = 0, then x = 2
Fraction = \(\frac { x }{ x + 3 }\) = \(\frac { 2 }{ 2 + 3 }\) = \(\frac { 2 }{ 5 }\)

Question 27.
Solution:
Let the denominator of a fraction = x
Then its numerator = x – 3

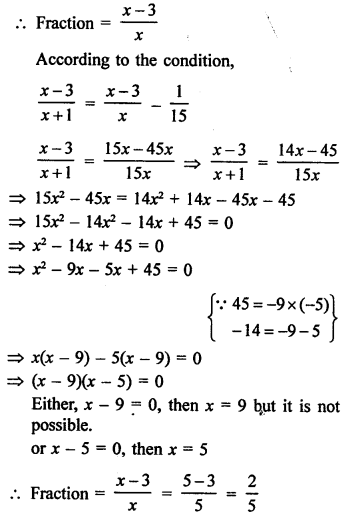
Question 28.
Solution:
Let the number = x
According to the condition,

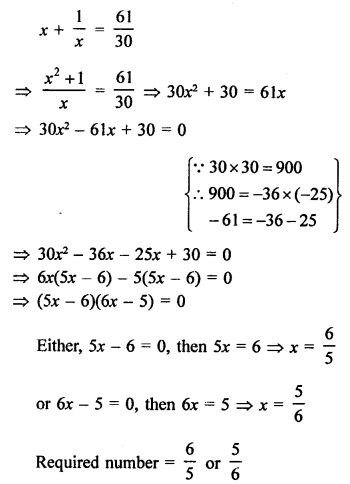
SOME GENERAL PROBLEMS
Question 29.
Solution:
Let number of students = x
According to the given condition,

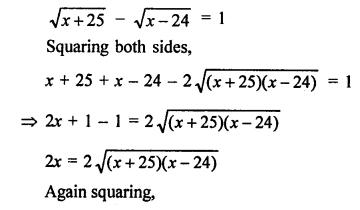
x² = (x + 25)(x – 24)
x² = x² + (25 – 24) x + 25 x (-24)
x² = x² + x – 600
x = 600
Number of students = 600

Question 30.
Solution:
Total number of apples = 300
Let number of students = x
Then according to the condition,

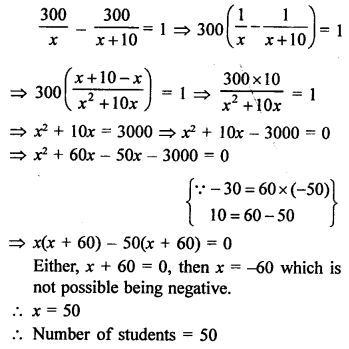
Question 31.
Solution:
Total number of marks = 40
Let marks in Mathematics = x
Then marks in English = 40 – x
According to the given condition,
(x + 3)(40 – x – 4) = 360
(x + 3)(36 – x) = 360
⇒ 36x – x² + 108 – 3x = 360
⇒ -x² + 33x + 108 – 360 = 0
⇒ -x² + 33x – 252 = 0
⇒ x² – 33x + 252 = 0
⇒ x² – 21x – 12x + 252 = 0
⇒ x(x – 21) – 12(x – 21) = 0
⇒ (x – 21)(x – 12) = 0
Either, x – 21 =0, then x = 21
or x – 11 = 0, then x = 11
Marks obtain in Mathematic and English = (21 and 19) or (12 or 28)

Question 32.
Solution:
Total budget = ₹ 2000
Let number of students = x
5 students failed to attend
Remaining students = x – 5
According to the condition,

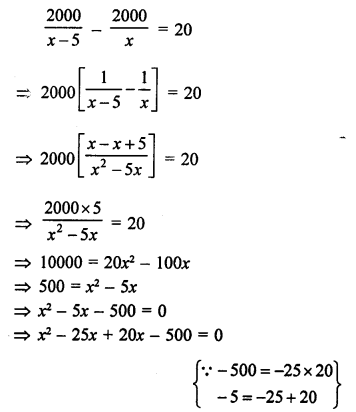
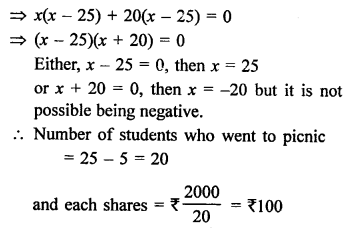
Question 33.
Solution:
Let original price of each book = ₹ x
and total amount = ₹ 600
Commission in price = ₹ 5 per book
According to the condition,

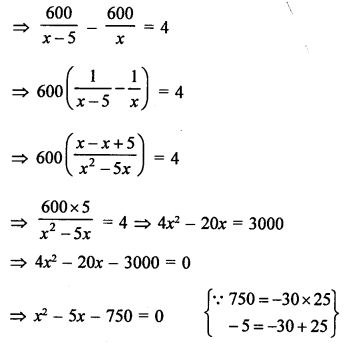
⇒ x² – 30x + 25x – 750 = 0
⇒ x(x – 30) + 25(x – 30) = 0
⇒ (x – 30)(x + 25) = 0
Either, x – 30 = 0, then x = 30
or x + 25 = 0, then x = -25 which is not possible being negative.
Original price of each book = ₹ 30
and number of books = \(\frac { 600 }{ 30 }\) = 20

Question 34.
Solution:
Total expenses on tour = ₹ 10800
Let number of days = x
According to the condition,

⇒ x(x + 24) – 20(x + 24) = 0
⇒ (x + 24)(x – 20) = 0
Either, x + 24 = 0, then x = -24 which is not possible being negative,
or x – 20 = 0, then x = 20
Number of days of tour = 20 days

Question 35.
Solution:
Total marks obtained = 28
Let marks in Mathematics = x
Then marks in Science = 28 – x
According to the condition,
(x + 3)(28 – x – 4) = 180
⇒ (x + 3)(24 – x) = 180
⇒ 24x – x² + 72 – 3x = 180
⇒ -x² + 21x – 180 + 72 = 0
⇒ x² – 21x + 108 = 0
⇒ x² – 12x – 9x + 108 = 0
⇒ x(x – 12) – 9(x – 12) = 0
⇒ (x – 12)(x – 9) = 0
Either, x – 12 = 0, then x = 12
or x – 9 = 0, then x = 9
Marks obtained in Mathematics and Science = (12, 16) or (9, 19)

Question 36.
Solution:
Amount = ₹ 180
Let number of pens purchased = x
According to the condition,

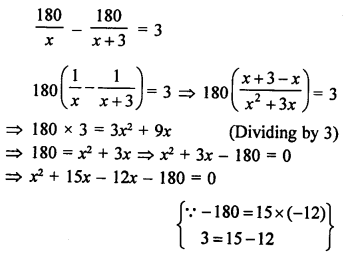
⇒ x(x + 15) – 12(x + 15) = 0
⇒ (x + 15) (x – 12) = 0
Either, x + 15 = 0, then x = -15 which is not possible being negative,
or x – 12 = 0, then x = 12
Number of pens purchased = 12

Question 37.
Solution:
S.P. of an article = ₹ 75
Gain % = C.P. of the article
Let gain % = x %
According to the condition,

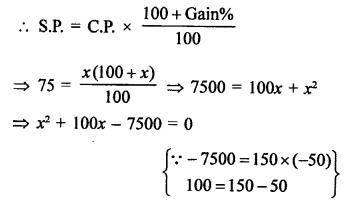
⇒ x² + 150x – 50x – 7500 = 0
⇒ x(x + 150) – 50(x + 150) = 0
⇒ (x + 150) (x – 50) = 0
Either, x + 150 = 0, then x = -150 which is not possible being negative,
or x – 50 = 0, then x = 50
Cost price of the article = ₹ 50

PROBLEMS ON AGES
Question 38.
Solution:
(i) Let present age of son = x years
His age 1 year ago = (x – 1) years
His father’s age = (x – 1) x 8
According to the condition,
(x – 1) x 8 + 1 = x2
⇒ 8x – 8 + 1 = x2
⇒ x² – 8x + 7 = 0
⇒ x² – x – 7x + 7 = 0
⇒ (x – 1)(x – 7) = 0
Either, x – 1 = 0, then x = 1 which is not possible.
or x – 7 = 0, then x = 7
Son’s age = 7 years
and his father’s age = (7)² = 49 years
(ii) Let the age of the son = x years
and the age of father = 3.5x years
According to the condition,
(x)² + (3.5x)² = 1325
⇒ x² + 12.25x² = 1325
⇒ 13.25x² = 1325
⇒ x² = 100
⇒ x = 10
Hence, the age of the son = 10 years
and the age of father 3.5 x 10 = 35 years

Question 39.
Solution:
Present age of Meena = x years
3 years ago her age = (x – 3) years
and 5 years hence, her age = (x + 5) years
According to the condition,

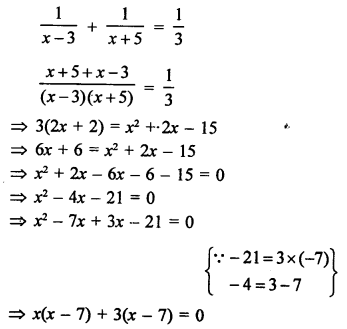
(x – 7) (x + 3) = 0
Either, x – 7 = 0, then x = 7
or x + 3 = 0, then x = -3 which is not possible being negative.
Her age = 7 years

Question 40.
Solution:
Sum of ages of a boy and his brother = 25 years
Let age of the boy = x years
Then age of his brother = (25 – x) years
According to the condition,
x (25 – x) = 126
⇒ 25x – x² – 126 = 0
⇒ x² – 25x + 126 = 0
⇒ x² – 18x – 7x + 126 = 0
⇒ x (x – 18) – 7 (x – 18) = 0
⇒ (x – 18) (x – 7) = 0
Either, x – 18 = 0, then x = 18
or x – 7 = 0, then x = 7
Age of boy = 7 years or 18 years
and age of his brother = 18 years or 7 years.

Question 41.
Solution:
Let present age of Tanvy = x years
Then 5 years ago her age = x – 5 years
8 years hence, her age = x + 8 years
According to the condition,
(x – 5) (x + 8) = 30
⇒ x² + 3x – 40 = 30
⇒ x² + 3x – 40 – 30 = 0
⇒ x² – 10x + 7x – 70 = 0
⇒ x (x – 10) + 7 (x – 10) = 0
⇒ (x – 10) (x + 7) = 0
Either, x – 10 = 0, then x = 10
or x + 7 = 0, then x = -7 which is not possible being negative.
Her present age = 10 years

Question 42.
Solution:
2 years ago,
Let son’s age = x years
and his father’s age = 3x²
Present age of son = (x + 2) years
and his father’s age = 3x² + 2
3 years hence, son’s age will be = x + 2 + 3 = x + 5 years
and age of his father = 3x² + 2 + 3 = (3x² + 5) years
According to the condition,
3x² + 5 = 4(x + 5)
⇒ 3x² + 5 = 4x + 20
⇒ 3x² – 4x + 5 – 20 = 0
⇒ 3x² – 4x – 15 = 0
⇒ 3x² – 9x + 5x – 15 = 0
⇒ 3x (x – 37) + 5 (x – 3) = 0
⇒ (x – 3)(3x + 5) = 0
Either, x – 3 = 0, then x = 3
or 3x + 5 = 0, then 3x = -5 ⇒ x = \(\frac { -5 }{ 3 }\) which is not possible being negative.
x = 3
Son’s present age = 3 + 2 = 5 years
and his father’s age = 3x² + 2
= 3 x (3)² + 2
= 27 + 2 = 29 years

PROBLEMS ON TIME AND DISTANCE
Question 43.
Solution:
Distance travelled = 150 km
Let the average speed of the truck = x km/hr

⇒ x (x – 60) + 10 (x – 60) 0
⇒ (x – 60) (x + 10) = 0
Either, x – 60 = 0, then x = 60
or x + 10 = 0, then x = -10 which is not possible being negative.
Original speed of the truck = 60 km/h

Question 44.
Solution:
Distance covered = 1500 km
Let original speed of the plane = x km/h

⇒ x² + 600x – 500x – 300000 = 0
⇒ x(x + 600) – 500(x + 600) = 0
⇒ (x + 600) (x – 500) = 0
Either, x + 600 = 0, then x = -600 which is not possible being negative.
or x – 500 = 0, then x = 500
Original speed of the plane = 500 km/hr
Yes, his promptness was appreciable.

Question 45.
Solution:
Distance covered by a train = 480 km
Let uniform speed = x km/h

⇒ x² – 40x + 32x – 1280 = 0
⇒ x(x – 40) + 32(x – 40) = 0
⇒ (x – 40) (x + 32) = 0
Either, x – 40 = 0, then x = 40
or x + 32 = 0, then x = -32 which is not possible being negative.
Speed of the train = 400 km/hr

Question 46.
Solution:
Distance covered = 54 km and then 63 km
Let first average speed = x km/hr
and next speed = (x + 6) km/hr
Total time taken = 3 hours
According to the condition,

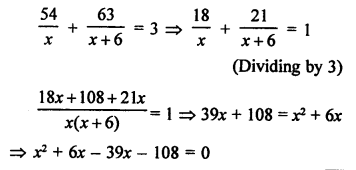
⇒ x² – 33x – 108 = 0
⇒ x² – 36x – 3x – 108 = 0
⇒ x (x – 36) + 3 (x – 36) = 0
⇒ (x – 36) (x + 3) = 0
Either, x – 36 = 0, then x = 36
or x + 3 = 0, then x – 3 which is not possible being negative.
Speed of the train = 36 km/hr.

Question 47.
Solution:
Distance travelled by a train =180 km
Let the uniform speed = x km/hr

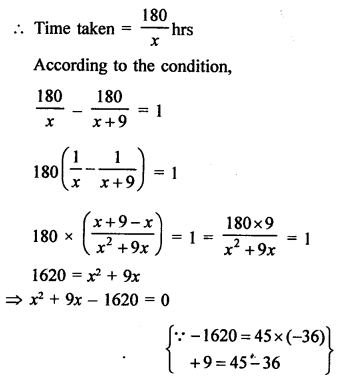
⇒ x² + 45x – 36x – 1620 = 0
⇒ x (x + 45) – 36 (x + 45) = 0
⇒ (x + 45) (x – 36) = 0
Either, x + 45 = 0, then x = -45 which is not possible being negative,
or (x – 36) = 0, then x = 36
Uniform speed of the train = 36 km/hr.

Question 48.
Solution:
Distance travelled = 300 km
Let the original speed of train be x km

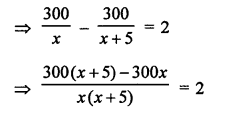
⇒ 300x + 1500 – 300x = 2x² + 10x
⇒ 2x² + 10x – 1500 = 0
⇒ x² + 5x – 750 = 0 (Dividing by 2)
⇒ x² + 30x – 25x – 750 = 0
⇒ x (x + 30) – 25 (x + 30) = 0
⇒ (x + 30) (x – 25) = 0
Either, x + 30 = 0 ⇒ x = -30 (Rejected ∵ speed cannot be negative)
or x – 25 = 0 ⇒ x = 25
Speed of the train = 25 km/hr

Question 49.
Solution:
Distance = 300 km
Let the speed of the passenger = x km/hr

⇒ x (x + 30) – 25 (x + 30) = 0
⇒ (x + 30) (x – 25) = 0
Either, x + 30 = 0, then x = -30 which is not possible being negative,
or x – 25 = 0, then x = 25
Speed of the train = 25 km/hr.

Question 50.
Solution:
Distance between Mumbai and Pune = 192 km
Let the speed of Deccan Queen = x km/hr
and speed of another train = (x – 20) km/hr
According to the condition,

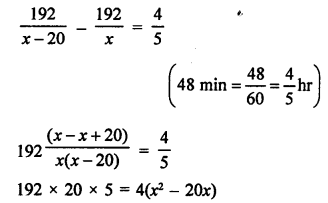
Question 51.
Solution:
Distance travelled = 24 km up and down
Speed of motor boat in still water = 18 km/hr
Let speed of stream = x km/hr
According to the condition,

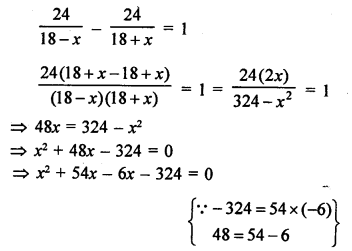
⇒ x (x + 54) – 6 (x + 54) = 0
⇒ (x + 54) (x – 6) = 0
Either, x + 54 = 0, then x = -54 which is not possible being negative,
or x – 6 = 0, then x = 6
Speed of stream = 6 km/hr

Question 52.
Solution:
Speed of a boat in still water = 8 km/hr
Let speed of water in stream = x km/hr
Total time taken = 5 hours
According to the condition,

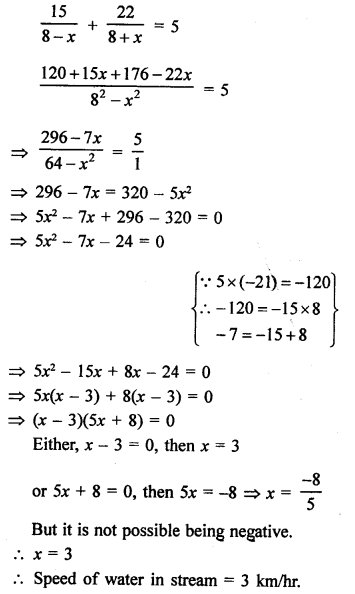
Question 53.
Solution:
Speed of motorboat in still water = 9 km/hr
Let speed of water = x km/hr
Total time taken = 3 hours
According to the condition,

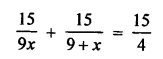
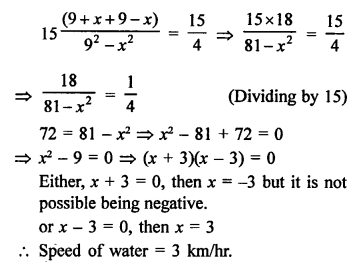
PROBLEMS ON TIME AND WORK AND PIPES AND CISTERN
Question 54.
Solution:
Let B finishes the work in = x days
Then A will finish it in = (x – 10) days
According to the condition,
(A + B)’s one day’s work

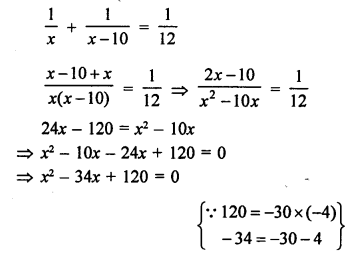
⇒ x² – 30x – 4x + 120 = 0
⇒ x (x – 30) – 4 (x – 30) = 0
⇒ (x – 30)(x – 4) = 0
Either, x – 30 = 0, then x = 30
or x – 4 = 0, then x = 4
But x = 4 is not possible
x = 30
B can finish the work in 30 days
and A can in 30 – 10 = 20 days.

Question 55.
Solution:
2 pipes can fill a cistern in 3\(\frac { 1 }{ 13 }\) = \(\frac { 40 }{ 13 }\) minutes
Let one pipe can fill it in = x minute
Then second will fill it in = (x + 3) minutes

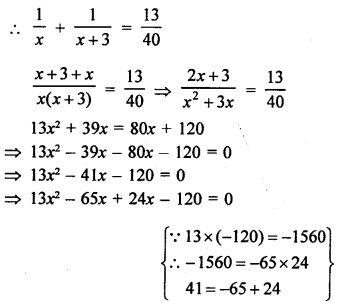
⇒ 13x (x – 5) + 24 (x – 5) = 0
⇒ (x – 5) (13x + 24) = 0
Either, x – 5 = 0, then x = 5
or 13x + 24 = 0
⇒ 13x = -24
⇒ x = \(\frac { -24 }{ 13 }\) which is not possible being negative.
x = 5
First pipe can fill the tank in 5 minutes
and second pipe will fill it in 5 + 3 = 8 minutes.

Question 56.
Solution:
Two pipes can fill a tank together in = 11\(\frac { 1 }{ 9 }\) = \(\frac { 100 }{ 9 }\) minutes
Let first pipe can fill it in = x minute
Then second pipe will fill it in = (x + 5) min
According to the condition,

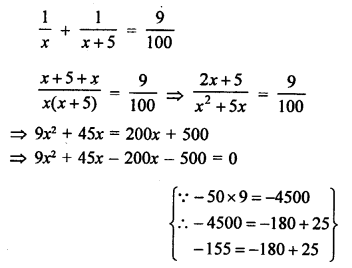
⇒ 9x² – 155x – 500 = 0
⇒ 9x² – 180x + 25x – 500 = 0
⇒ 9x (x – 20) + 25(x – 20) = 0
⇒ (x – 20) (9x + 25) = 0
Either, x – 20 = 0, then x = 20
or 9x + 25 = 0, then 9x = -25 ⇒ x = \(\frac { -25 }{ 9 }\)
But it is not possible being negative.
First pipe will fill it in 20 minutes
and second will fill in = 20 + 5 = 25 minutes-

Question 57.
Solution:
Two water taps together can fill a tank in = 6 hours
Let first tap of larger diameter can fill it in x hour
Then second tap will fill it in (x – 9) hour
According to the condition,

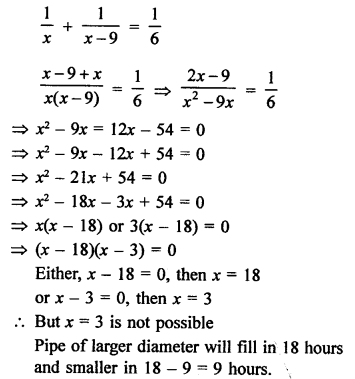
PROBLEMS ON AREA AND GEOMETRY
Question 58.
Solution:
Let breadth of a rectangle (b) = x cm
Then length (l) = 2x cm
Area = l x b = 2x x x
2x x x = 288
⇒ 2x² = 288
⇒ x² = 144 = (12)²
x = 12
Length = 2x = 2 x 12 = 24 cm
and breadth = x = 12 cm

Question 59.
Solution:
Let breadth of a rectangular field (b) = x m
Then its length (l) = 3x m
Area = l x b = 3x x x = 3x²
3x² = 147
⇒ x² = 49 = (7)²
x = 7
Length = 3x = 3 x 7 = 21 m
and breadth = x = 7 m

Question 60.
Solution:
Let breadth of a hall (b) = x m
Then its length (l) = (x + 3) m
Area = l x b = (x + 3) x x = x² + 3x
x² + 3x = 238
⇒ x² + 3x – 238 = 0
⇒ x² + 11x – 14x – 238 = 0
⇒ x (x + 17) – 14 (x – 17) = 0
⇒ (x + 17) (x – 14) = 0
Either, x + 17 = 0, then x = -17 which is not possible being negative.
or x – 14 = 0, then x = 14
Breadth = 14 m
and length = 14 + 3 = 17 m

Question 61.
Solution:
Perimeter of a rectangular plot = 62 m
and area = 228 m²
Let length of plot = x m
Then width = \(\frac { 62 }{ 2 }\) – x = 31 – x
Area = l x b = x (31 – x)
x (31 – x) = 228
⇒ 31x – x² = 228
⇒ x² – 31x + 228 = 0
⇒ x² – 19x – 12x + 228 = 0
⇒ x (x – 19) – 12 (x – 19) = 0
⇒ (x – 19) (x – 12) = 0
Either, x – 19 = 0, then x = 19
or x – 12 = 0, then x = 12
If length is 19 m, then breadth = 31 – 19 = 12 m
and if length is 12 m then breadth = 31 – 12 = 19 m
which is not possible as length > breadth
Dimensions are (19, 12) m

Question 62.
Solution:
Area of path around it = 120 m²
Length of a rectangular field (l) = 16 m
and breadth (b) = 10 m
Let a path of x m wide be made around it, then its
Outer length (L) = (16 + 2x) m
and breadth (B) = (10 + 2x) m
Area of path = L x B – l x b
= (16 + 2x) (10 + 2x) – 16 x 10
⇒ 160 + 52x + 4x² – 160 = 120
⇒ 4x² + 52x – 120 = 0
⇒ x² + 13x – 30 = 0 (Dividing by 4)
⇒ x² + 15x – 2x – 30 = 0
⇒ x (x + 15) – 2 (x + 15) = 0
⇒ (x + 15) (x – 2) = 0
Either, x + 15 = 0, then x = -15 which is not possible being negative,
or x – 2 = 0, then x = 2
Width of path = 2 m

Question 63.
Solution:
The sum of areas of two squares = 640 m²
and difference between their perimeters = 64 m
Let 4 sides of first square = x m
Then perimeter = 4x
Perimeter of second square = 4x – 64
and side = \(\frac { 4x – 64 }{ 4 }\) = (x – 16) m
Now sum of their areas,
x² + (x – 16)² = 640
⇒ x² + x² – 32x + 256 = 640
⇒ 2x² – 32x + 256 – 640 = 0
⇒ 2x² – 32x – 384 = 0
⇒ x² – 16x – 192 = 0
⇒ x² – 24x + 8x – 192 = 0
⇒ x (x – 24) + 8 (x – 24) = 0
⇒ (x – 24) (x + 8) = 0
Either, x – 24 = 0, then x = 24
or x + 8 = 0, then x = -8 which not possible being negative,
x = 24
Side of first square = 24 m
and side of second square = 24 – 16 = 8 m

Question 64.
Solution:
Let side of a square = x m
Then length of rectangle = 3x m
and width = (x – 4) m

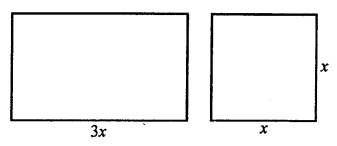
Now area of square = x² m²
and area of rectangle = l x b = (3x) x (x – 4) m²
According to the condition,
x² = 3x (x – 4)
⇒ x² = 3x² – 12x
⇒ 3x² – 12x – x2 = 0
⇒ 2x² – 12x = 0
⇒ 2x (x – 6) = 0
⇒ x – 6 = 0
⇒ x = 6m
Side of square = 6 m
and length of rectangle = 3 x 6 m = 18m
and width = x – 4 = 6 – 4 = 2m

Question 65.
Solution:
Area of a rectangular garden = 180 sq m
Let length of garden = x m

Question 66.
Solution:
Area of a right triangle = 600 cm²
Let altitude = x cm
Then base = (x + 10) cm

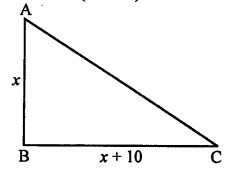
Area = \(\frac { 1 }{ 2 }\) base x altitude
600 = \(\frac { 1 }{ 2 }\) x (x + 10) x
x² + 10x = 1200
⇒ x² + 10x – 1200 = 0
⇒ x² + 40x – 30x – 1200 = 0
⇒ x (x + 40) – 30 (x + 40) = 0
⇒ (x + 40) (x – 30) = 0
Either, x + 40 = 0, then x = -40 which is not possible being negative.
or x – 30 = 0, then x = 30
Altitude = 30 cm
Base = 30 + 10 = 40 cm

Question 67.
Solution:
Area of right triangle = 96 sq. m
Let altitude of the triangle = x m
Then base = 3x m
Area = \(\frac { 1 }{ 2 }\) x base x altitude
96 = \(\frac { 1 }{ 2 }\) x 3x x x
⇒ 3x² = 96 x 2
x² = 64 = (8)²
x = 8 m
Base = 3x = 3 x 8 = 24m
and altitude = x = 8 m

Question 68.
Solution:
Area of right triangle = 165 sq m
Let altitude = x m
Then base = – (x + 7) m
Area = \(\frac { 1 }{ 2 }\) x base x altitude
165 = \(\frac { 1 }{ 2 }\) x x x (x + 7)
330 = x² + 7x
⇒ x² + 7x – 330 = 0
⇒ x² + 22x – 15x – 330 = 0
⇒ x (x + 22) – 15 (x + 22) = 0
⇒ (x + 22) (x – 15) = 0
Either, x + 22 = 0, then x = -22 which is not possible being negative,
or x – 15 = 0, then x = 15
Altitude = x + 7 = 15 + 7 = 22m
and base = x = 15 m

Question 69.
Solution:
In a right triangle,
Hypotenuse = 20 m
Difference of other two sides = 4 m
Let first side = x m
Then second side = (x + 4) m
According to the condition,
(x)² + (x + 4)² = (20)²
⇒ x² + x² + 8x + 16 = 400
⇒ 2x² + 8x + 16 – 400 = 0
⇒ 2x² + 8x – 384 = 0
⇒ x² + 4x – 192 = 0
⇒ x² + 16x – 12x – 192 = 0
⇒ x (x + 16) – 12 (x + 16) = 0
⇒ (x + 16) (x – 12) = 0
Either, x + 16 = 0, then x = -16 which is not possible being negative,
or x – 12 = 0, then x = 12
First side = 12 m
Second side = x + 4= 12 + 4 = 16 m

Question 70.
Solution:
In a right triangle, let base = x m
Length of hypotenuse = (x + 2) m

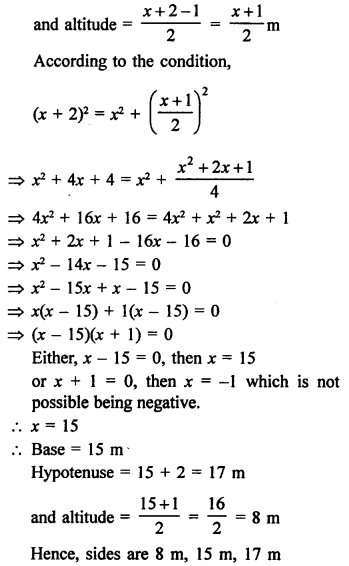
Question 71.
Solution:
Let shorter side of a right triangle = x m
Then hypotenuse = (2x – 1) m
and longer side = (x + 1) m
According to the condition,
(2x – 1)² = x² + (x + 1)² (Use of Pythagoras Theorem)
⇒ 4x² – 4x + 1 = x² + x² + 2x + 1
⇒ 4x² – 4x + 1 – x² – x² – 2x – 1 = 0
⇒ 2x² – 6x = 0
⇒ 2x (x – 3) = 0
⇒ x – 3 = 0
⇒ x = 3
Shorter side = 3 m
Hypotenuse = 2x – 1 = 3 x 2 – 1 = 6 – 1 = 5 m
and longer side = x + 1 = 3 + 1 = 4m
Sides 3 m, 4 m, 5 m

Hope given RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10E are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.