RS Aggarwal Class 10 Solutions Chapter 10 Quadratic Equations Ex 10D

RS Aggarwal Class 10 Solutions Chapter 10 Quadratic Equations Ex 10D

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10D.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10A
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10B
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10C
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10D
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10E
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Test Yourself

Question 1.
Solution:

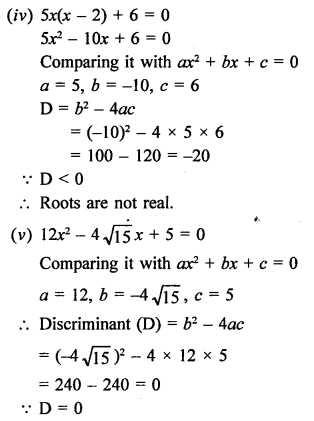
Question 2.
Solution:

Question 3.
Solution:
x² + px – q² = 0
Comparing it with ax² + bx + c = 0
a = 1, b = p, c = -q²
Discriminant (D) = b² – 4ac
= (p)² – 4 x 1 x (-q²)
= p² + 4 q²
p and q are of two powers
p² + 4q² is always greater than 0
The roots are real for all real values of p and q.

Question 4.
Solution:
The quadratic equation is 3x² + 2kx + 27 = 0
Comparing it with ax² + bx + c = 0
a = 3, b = 2k, c = 27
Discriminant (D) = b² – 4ac
= (2k)² – 4 x 3 x 27
= (2k)² – 324
Roots are real and equal
(2k)² – 324 = 0
⇒ (2k)² – (18)² = 0
⇒ (k)² – (9)² = 0
⇒ (k + 9) (k – 9) = 0
Either k + 9 = 0, then k = -9
or k – 9 = 0, then k = 9
Hence, k = 9, -9

Question 5.
Solution:
The quadratic equation is
kx (x – 2√5) x + 10 = 0
kx² – 2√5 kx + 10 = 0
Comparing it with ax² + bx + c = 0
a = k, b = -2√5 k, c = 10
D = b² – 4ac = (-2 k)² – 4 x k x 10 = 20k² – 40k
Roots are real and equal.
D = 0
20k² – 40k = 0
⇒ k² – 2k = 0
⇒ k (k – 2) = 0
Either, k = 0 or k – 2 = 0, then k = 2
k = 0, k = 2

Question 6.
Solution:
The quadratic equation is 4x² + px + 3 = 0
Comparing it with ax² + bx + c = 0
a = 4, b = p, c = 3
D = b² – 4ac = p² – 4 x 4 x 3 = p²- 48
Roots are real and equal.
D = 0
⇒ p² – 48 = 0
⇒ p² = 48 = (±4√3)²
⇒ P = ± 4√3
P = 4√3, p = -4√3

Question 7.
Solution:
The quadratic equation is 9x² – 3kx + k = 0
Comparing it with ax? + bx + c = 0
a = 9, b = -3k, c = k
D = b² – 4ac = (-3k)² – 4 x 9 x k = 9k² – 36k
Roots are real and equal.
D = 0
9k² – 36k = 0
⇒ 9k (k – 4) = 0
Either, k = 0 or k – 4 = 0, then k = 4
The value of k is non-zero.
k = 4

Question 8.
Solution:
(i) The equation is (3k + 1) x² + 2(k + 1) x + 1 = 0
Comparing it with ax² + bx + c = 0
a = (3k + 1), b = 2(k + 1), c = 1
D = b² – 4 ac
= [2(k + 1)]² – 4(3k + 1) x 1
= 4k² + 4 + 8k – 12k – 4
= 4k² – 4k
= 4k (k – 1)
Roots are real and equal.
Either, k = 0 or k – 1 = 0, then k = 1
k = 0, k = 1
(ii) x² + k(2x + k – 1) + 2 = 0
⇒ x² + 2kx + (k² – k + 2) = 0
Here, a = 1, b = 2k, c = (k² – k + 2)
Discriminant (D) = b² – 4ac = (2k)² – 4 x 1 x (k² – k + 2)
= 4k² – 4k² + 4k – 8
= 4k – 8
Roots are real and equal.
D = 0
⇒ 4k – 8 = 0
⇒ k = 2
Hence, k = 2

Question 9.
Solution:

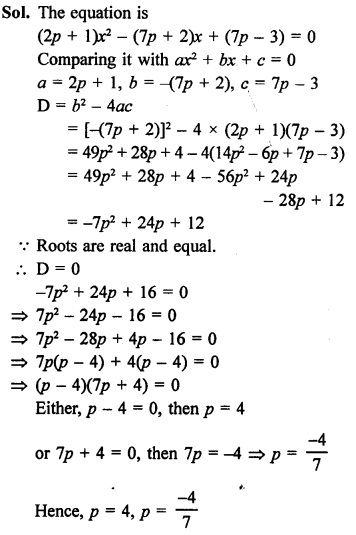
Question 10.
Solution:
The given quadratic equation is
(p + 1) x² – 6(p + 1) x + 3(p + 9) = 0, p ≠ -1

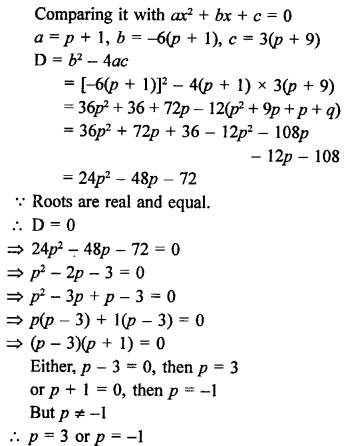
Question 11.
Solution:
-5 is a root of 2x² + px – 15 = 0
x = -5 will satisfy it
Now, substituting the value of x = -5
⇒ 2(-5)² + p(-5) – 15 = 0
⇒ 50 – 5p – 15 = 0
⇒ 35 – 5p = 0
⇒ 5p = 35
⇒ P = 7
In quadratic equation p(x² + x) + k = 0
⇒ 7 (x² + x) + k = 0 (p = 7)
⇒ 7x² + 7x + k = 0
Comparing it with ax² + bx + c = 0
a = 7, b = 7, c = k
D = b² – 4ac = (7)² – 4 x 7 x k
= 49 – 28k
Roots are real and equal.
49 – 28k = 0
⇒ 28k = 49
k = \(\frac { 49 }{ 28 }\) = \(\frac { 7 }{ 4 }\)

Question 12.
Solution:
3 is a root of equation x² – x + k = 0
It will satisfy it
Now, substituting the value of x = 3 in it
(3)² – (3) + k = 0
⇒ 9 – 3 + k = 0
⇒ 6 + k = 0
⇒ k = -6
Now in the equation, x² + k (2x + k + 2) + p = 0
x² + (-6)(2x – 6 + 2) + p = 0
⇒ x² – 12x + 36 – 12 + p = 0
⇒ x² – 12x + (24 + p) = 0
Comparing it with ax² + bx + c = 0
a = 1, b = -12, c = 24 + p
D = b² – 4ac
= (-12)² – 4 x 1 x (24 + p)
= 144 – 96 – 4p = 48 – 4p
Roots are real and equal.
D = 0
48 – 4p = 0
⇒ 4p = 48
⇒ p = 12
Hence, p = 12

Question 13.
Solution:
-4 is a root of the equation x² + 2x + 4p = 0
Then it will satisfy the equation
Now, substituting the value of x = -4
(-4)² + 2(-4) + 4p = 0
16 – 8 + 4p = 0
⇒ 8 + 4p = 0
⇒ 4p = -8
⇒ p = -2
In the quadratic equation x² + px (1 + 3k) + 7(3 + 2k) = 0
⇒ x² – 2x (1 + 3k) + 7(3 + 2k) = 0
Comparing it with ax² + bx + c = 0
a = 1, b = -2 (1 + 3k), c = 7 (3 + 2k)
D = b² – 4ac
= [-2(1 + 3k)]² – 4 x 1 x 7(3 + 2k)
= 4(1 + 9k² + 6k) – 28(3 + 2k)
= 4 + 36k² + 24k – 84 – 56k
= 36k² – 32k – 80
Roots are equal.
D = 0
⇒ 36k² – 32k – 80 = 0
⇒ 9k² – 8k – 20 = 0
⇒ 9k² – 18k + 10k – 20 = 0
⇒ 9k (k – 2) + 10(k – 2) = 0
⇒ (k – 2) (9k + 10) = 0
Either, k – 2 = 0, then k = 2
or 9k + 10 = 0, then 9k = -10 ⇒ k = \(\frac { -10 }{ 9 }\)
k = 2, k = \(\frac { -10 }{ 9 }\)

Question 14.
Solution:

Question 15.
Solution:

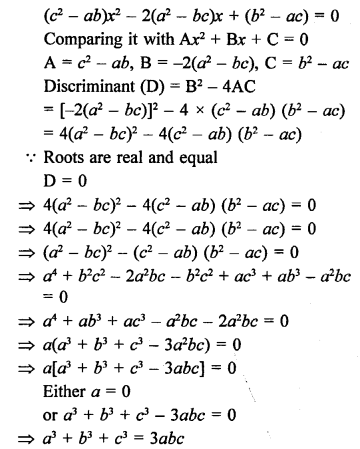
Question 16.
Solution:
The quadratic equation is 2x² + px + 8 = 0
Comparing it with ax² + bx + c = 0
a = 2, b = p, c = 8
D = b² – 4ac = p² – 4 x 2 x 8 = p² – 64
Roots are real.
D ≥ 0
p² – 64 ≥ 0
⇒ p² ≥ 64 ≥ (±8)²
p ≥ 8 or p ≤ -8

Question 17.
Solution:

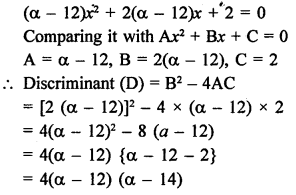
Roots are equal
D = 0
⇒ 4(α – 12) (α – 14) = 0
⇒ α – 14 = 0 {(α – 12) ≠ 0}
⇒ α = 14
Hence, α = 14

Question 18.
Solution:
9x² + 8kx + 16 = 0
Comparing it with ax² + bx + c = 0
a = 9, b = 8k, c = 16
D = b² – 4ac
= (8k)² – 4 x 9 x 16 = 64k² – 576
Roots are real and equal.
D = 0
64k² – 576 = 0
64k² = 576
⇒ k² = 9 = (±3)²
k = 3, k = -3

Question 19.
Solution:

Question 20.
Solution:

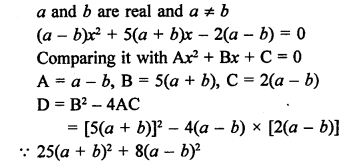
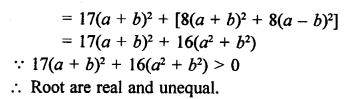
Question 21.
Solution:

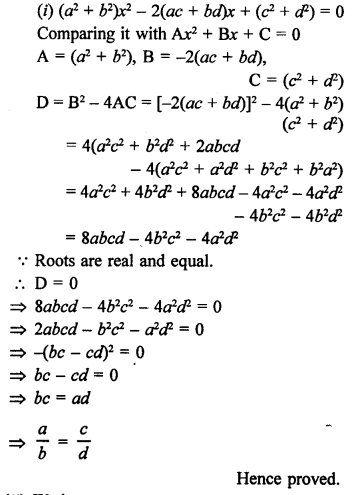
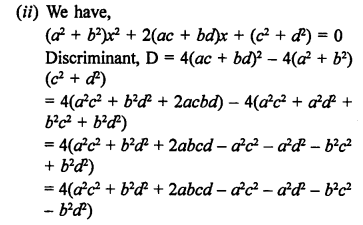
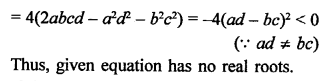
Question 22.
Solution:

Hope given RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.