Online Education for RS Aggarwal Class 10 Solutions Chapter 10 Quadratic Equations Test Yourself

Online Education for RS Aggarwal Class 10 Solutions Chapter 10 Quadratic Equations Test Yourself

These Solutions are part of Online Education RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Test Yourself.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10A
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10B
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10C
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10D
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Ex 10E
• RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Test Yourself

Objective Questions (MCQ)
Question 1.
Solution:
(a) x² – 3√x + 2 = 0
It is not a quadratic equation, it has a fractional power of √x
(b) x + \(\frac { 1 }{ x }\) = x²
⇒ x² + 1 = x³
It is not a quadratic equation.
(c) x² + \(\frac { 1 }{ { x }^{ 2 } }\) = 5
⇒ x⁴ + 1 + 5x²
It is not a quadratic equation.
(d) 2x² – 5x = (x – 1)²
⇒ 2x² – 5x = x² – 2x + 1
⇒ x² – 3x – 1 = 0
It is a quadratic equation. (d)

Question 2.
Solution:
(a) (x² + 1) = (2 – x)² + 3
⇒ x² + 1 = 4 + x² – 4x + 3 is not a quadratic equation.
(b) x³ – x² = (x – 1)³
⇒ x³ – x² = x³ – 3x² + 3x – 1
⇒ 3x² – x² – 3x + 1 = 0
⇒ 2x² – 3x + 1 = 0
It is a quadratic equation.
(c) 2x² + 3 = 10x – 15 + 2x² – 3x
⇒ 3x – 15 – 3 = 0
It is not a quadratic equation. (b)

Question 3.
Solution:
(a) It is a quadratic equation.
(b) (x + 2)² = 2(x² – 5)
⇒ x² + 4x + 4 = 2x² – 10
⇒ x² – 4x – 14 = 0
It is a quadratic equation.
(c) (√2 x + 3)² = 2x² + 6
⇒ 2x² + 3√2 x + 9 = 2x² + 6
⇒ 3√2 + 3 = 0
It is not a quadratic equation.
(d) (x – 1)² = 3x² + x – 2
⇒ x² – 2x +1 = 3x² + x – 2
⇒ 2x² + 3x – 3 = 0
It is a quadratic equation. (c)

Question 4.
Solution:
x = 3 is solution of 3x² + (k – 1)x + 9 = 0
It will satisfy it
3(3)² + (k – 1)(3) + 9 = 0
⇒ 27 + 3k – 3 + 9 = 0
⇒ 3k + 33 = 0
⇒ k = -11 (b)

Question 5.
Solution:
2 is one root of equation 2x² + ax + 6 = 0
It will satisfy it
2(2)² + a(2) + 6 = 0
⇒ 8 + 2a + 6 = 0
⇒ 2a = -14
⇒ a = -7
a = -7 (b)

Question 6.
Solution:
In equation x² – 6x + 2 = 0
Sum of roots = \(\frac { -b }{ a }\) = \(\frac { -(-6) }{ 1 }\) = 6 (c)

Question 7.
Solution:
In equation x² – 3x + k = 10
x² – 3x + (k – 10) = 0
Product of roots = \(\frac { c }{ a }\) = \(\frac { k – 10 }{ 1 }\) = k – 10
k – 10 = -2 then k = 10 – 2 = 8 (c)

Question 8.
Solution:
In equation 7x² – 12x + 18 = 0

Question 9.
Solution:
In equation 3x² – 10x + 3 = 0

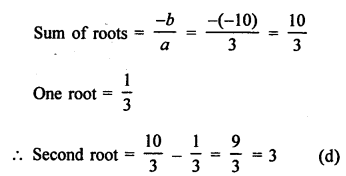
Question 10.
Solution:
In equation 5x² + 13x + k = 0

Question 11.
Solution:
In equation kx² + 2x + 3k = 0
Sum of roots = \(\frac { -b }{ a }\) = \(\frac { -2 }{ k }\)

Question 12.
Solution:
Roots of an equation are 5, -2
Sum of roots (S) = 5 – 2 = 3
and product (P) = 5 x (-2) = -10
Equation will be
x² – (S)x + (P) = 0
⇒ x² – 3x – 10 = 0 (b)

Question 13.
Solution:
Sum of roots (S) = 6
Product of roots (P) = 6
Equation will be x² – (S)x + (P) = 0
x² – 6x + 6 = 0 (a)

Question 14.
Solution:
α and β are the roots of the equation 3x² + 8x + 2 = 0

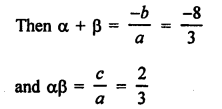
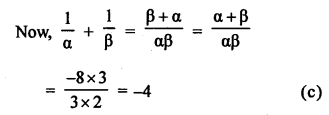
Question 15.
Solution:
In equation ax² + bx + c = 0

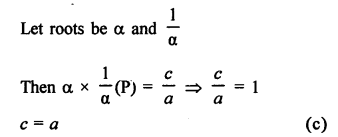
Question 16.
Solution:
In equation ax² + bx + c = 0
Let α and β are the roots, then

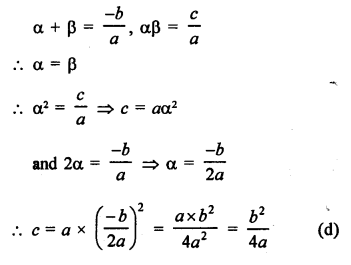
Question 17.
Solution:
In equation 9x² + 6kx + 4 = 0, roots are equal
Let roots be α, α then

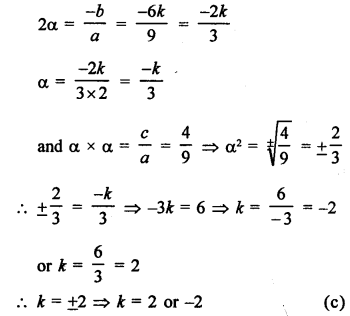
Question 18.
Solution:
In equation x² + 2 (k + 2) x + 9k = 0
Roots are equal
Let α, α be the roots, then

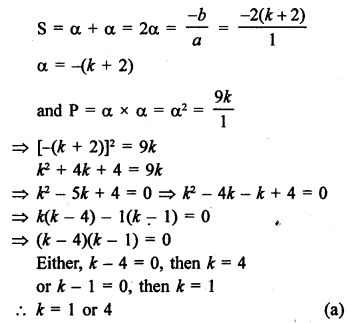
Question 19.
Solution:
In the equation
4x² – 3kx + 1 = 0 roots are equal
Let α, α be the roots

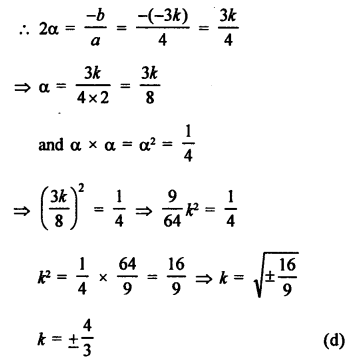
Question 20.
Solution:
Roots of ax² + bx + c = 0, a ≠ 0 are real and unequal if D > 0
⇒ b² – 4ac > 0 (a)

Question 21.
Solution:
In the equation ax² + bx + c = 0
D = b² – 4ac > 0, then roots are real and unequal. (b)

Question 22.
Solution:
In the equation 2x² – 6x + 7 = 0
D = b² – 4ac = (-6)² – 4 x 2 x 7 = 36 – 56 = -20 < 0
Roots are imaginary (not real) (d)

Question 23.
Solution:
In equation 2x² – 6x + 3 = 0
D = b² – 4ac = (-6)² – 4 x 2 x 3 = 36 – 24 = 12 > 0
Roots are real, unequal and irrational, (b)

Question 24.
Solution:
In equation 5x² – kx + 1 = 0
D = b² – 4ac = (-k)² – 4 x 5 x 1 = k² – 20
Roots are real and distinct
D > 0
⇒ k² – 20 > 0
⇒ k² > 20
⇒ k > √±20
⇒ k > ±2√5
⇒ k > 2√5 or k < -2√5 (d)

Question 25.
Solution:
In equation x² + 5kx + 16 = 0
D = b² – 4ac = (5k)² – 4 x 1 x 16

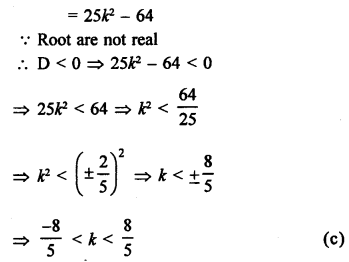
Question 26.
Solution:
The equation x² – kx + 1 = 0
D = b2 – 4ac = (-k)² – 4 x 1 x 1 ⇒ k² – 4
Roots are not real
D < 0
⇒ k² – 4 < 0
⇒ k² < 4
⇒k < (±2)²
⇒ k < ±2
-2 < k < 2 (c)

Question 27.
Solution:
In the equation kx² – 6x – 2 = 0

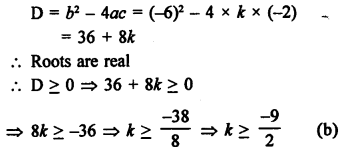
Question 28.
Solution:
Let the number be = x

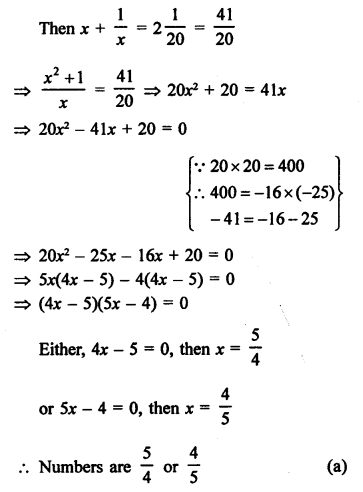
Question 29.
Solution:
Perimeter of a rectangle = 82 m
and Area = 400
Let breadth (b) = x, then
Length = \(\frac { P }{ 2 }\) – x = \(\frac { 82 }{ 2 }\) – x = 41 – x
Area = lb
400 = x (41 – x) = 41x – x²
⇒ x² – 41x + 400 = 0
⇒ x² – 25x – 16x + 400 = 0
⇒ x (x – 25) – 16(x – 25) = 0
⇒ (x – 25) (x – 16) = 0
Either, x – 16 = 0, then x = 16
or x – 25 = 0, then x = 25
Breadth = 16 m (c)

Question 30.
Solution:
Let breadth of a rectangular field = x m
Then length = (x + 8) m
and area = 240 m²
x (x + 8) = 240
⇒ x² + 8x – 240 = 0
⇒ x² + 20x – 12x – 240 = 0
⇒ x (x + 20) – 12 (x + 20) = 0
⇒ (x + 20) (x – 12) = 0
Either, x + 20 = 0, then x = -20 which is not possible being negative,
or x – 12 = 0, then x = 12
Breadth = 12 m (c)

Question 31.
Solution:
2x² – x – 6 = 0

Very-Short-Answer Questions
Question 32.
Solution:
Sum of two natural numbers = 8
Let first number – x
Then second number = 8 – x
According to the condition,
x (8 – x) = 15
⇒ 8x – x² = 15
⇒ x² – 8x + 15 = 0
⇒ x² – 3x – 5x + 15 = 0
⇒ x(x – 3) – 5(x – 3) = 0
⇒ (x – 3)(x – 5) = 0
Either, x – 3 = 0, then x = 3
or x – 5 = 0, then x = 5
Natural numbers are 3, 5

Question 33.
Solution:
x = -3 is a solution of equation x² + 6x + 9 = 0 Then it will satisfy it
LHS = x² + 6x + 9 = (-3)² + 6(-3) + 9 = 9 – 18 + 9 = 0 = RHS

Question 34.
Solution:
3x² + 13x + 14 = 0
If x = -2 is its root then it will satisfy it
LHS = 3(-2)² + 13(-2) + 14 = 3 x 4 – 26 + 14 = 12 – 26 + 14 = 26 – 26 = 0 = RHS

Question 35.
Solution:
x = y is a solution of equation 3x² + 2kx – 3 = 0, then it will satisfy it

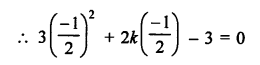
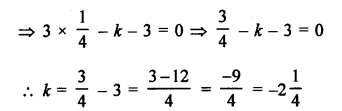
Question 36.
Solution:
2x² – x – 6 = 0
⇒ 2x² – 4x + 3x – 6 = 0

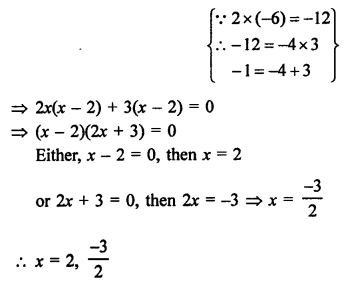
Question 37.
Solution:
3√3 x² + 10x + √3 = 0

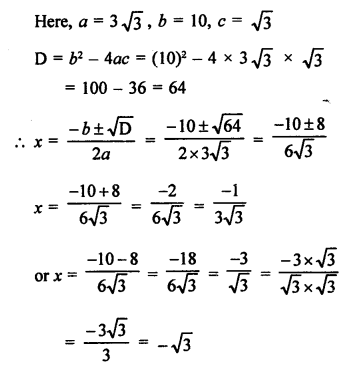
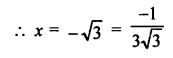
Question 38.
Solution:
Roots of the quadratic equation 2x² + 8x + k = 0 are equal
Let α, α be its roots, then

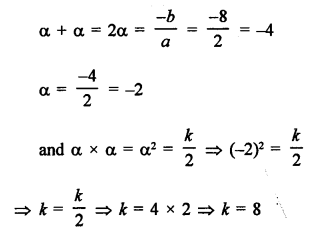
Question 39.
Solution:
px² – 2√5 px + 15 = 0
Here, a = p, b = 2√5 p, c = 15
D = b² – 4ac = (-2√5 p)² – 4 x p x 15 = 20p² – 60p
Roots are equal.
D = 0
⇒ 20p² – 60p = 0
⇒ p² – 3p = 0
⇒ p (p – 3) = 0
p – 3 = 0, then p = 3

Question 40.
Solution:
1 is a root of equation
ay² + ay + 3 = 0 and y² + y + b = 0
Then a(1)² + a(1) + 3 = 0
⇒ a + a + 3 = 0
⇒ 2a + 3 = 0
⇒ a = \(\frac { -3 }{ 2 }\)
and 1 + 1 + b = 0
⇒ 2 + b = 0
⇒ b = -2
ab = \(\frac { -3 }{ 2 }\) x (-2) = 3
Hence, ab = 3

Question 41.
Solution:
The polynomial is x² – 4x + 1
Here, a = 1, b = -4, c = 1

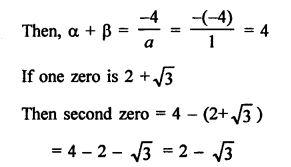
Question 42.
Solution:
In the quadratic equation 3x² – 10x + k = 0

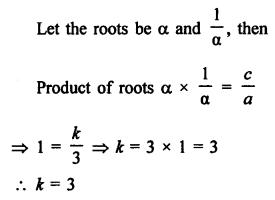
Question 43.
Solution:
The quadratic equation is
px (x – 2) + 6 = 0
⇒ px² – 2px + 6 = 0
D = b² – 4ac = (-2p)² – 4 x p x 6 = 4p² – 24p
Roots are equal
D = 0
Then 4p² – 24p = 0
⇒ 4p (p – 6) = 0
⇒ p – 6 = 0
⇒ p = 6

Question 44.
Solution:
x² – 4kx + k = 0
D = b² – 4ac = (-4k)² – 4 x 1 x k = 16k² – 4k
Roots are equal
D = 0
16k² – 4k = 0
⇒ 4k (4k – 1) = 0
⇒ 4k – 1 = 0
⇒ k = \(\frac { 1 }{ 4 }\)

Question 45.
Solution:
9x² – 3kx + k = 0
D = b² – 4ac = (-3k)² – 4 x 9 x k = 9k² – 36k
Roots are equal
D = 0
9k² – 36k = 0
9k (k – 4) = 0
Either, 9k = 0, then k = 0
or (k – 4) = 0 ⇒ k = 4
k = 0, 4

Short-Answer Questions
Question 46.
Solution:
x² – (√3 + 1) x + √3 = 0
D = b² – 4ac
= [-(√3 + 1)]² – 4 x 1 x √3
= 3 + 1 + 2√3 – 4√3
= 4 + 2√3 – 4√3
= 4 – 2√3
= 3 + 1 – 2√3
= (√3 – 1)²

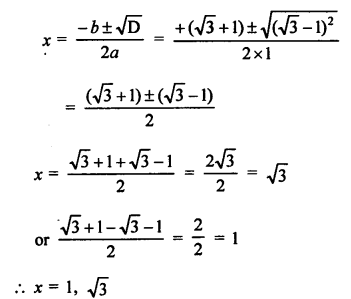
Question 47.
Solution:
2x² + ax – a² = 0
D = B² – 4AC = a² – 4 x 2(-a)² = a² + 8a² = 9a²

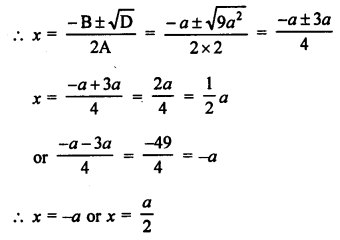
Question 48.
Solution:
3x² + 5√5 x – 10 = 0
D = b² – 4ac = (5√5)² – 4 x 3 x (-10)
= 125 + 120 = 245 = 49 x 5 = (7√5)²

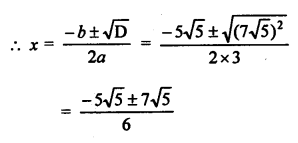
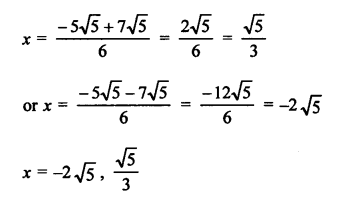
Question 49.
Solution:
√3 x² + 10x – 8√3 = 0

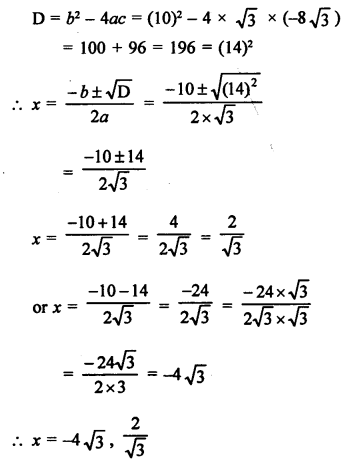
Question 50.
Solution:
√3 x² – 2√2 x – 2√3 = 0

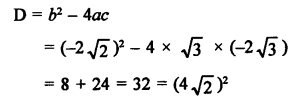
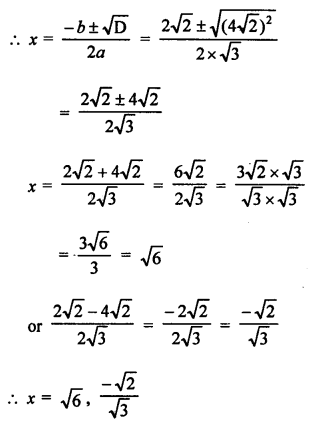
Question 51.
Solution:
4√3 x² + 5x – 2√3 = 0

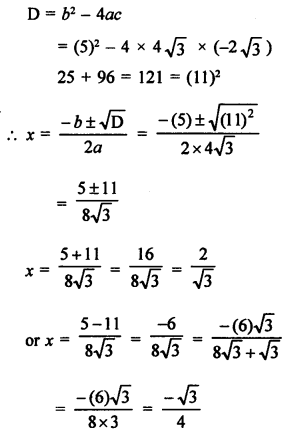
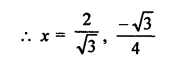
Question 52.
Solution:
4x² + 4bx – (a² – b²) = 0

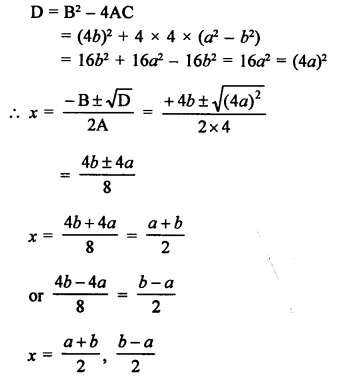
Question 53.
Solution:
x² + 5x – (a² + a – 6) = 0
a² + a – 6 = a² + 3a – 2a – 6 = a(a + 3) – 2(a + 3) = (a + 3)(a – 2)
and 6 = (a + 3) – (a – 2)
x² + (a + 3)x – (a – 2)x – (a + 3) (a – 2) = 0
x (x + a + 3) – (a – 2) (x + a + 3) = 0
(x + a + 3)(x – a + 2) = 0
Either, x + a + 3 = 0, then x = -(a + 3)
or x – a + 2 = -0 then x = (a – 2)
x = -(a + 3) or (a – 2)

Question 54.
Solution:
x² + 6x – (a² + 2a – 8) = 0

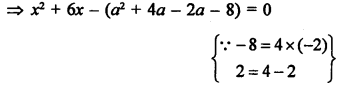
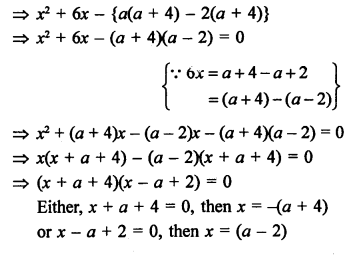
Question 55.
Solution:
x² – 4ax + 4a² – b² = 0
4a² – b² = (2a)² – (b)² = (2a + b)(2a – b) – 4ax = (2a + b)x + (2a – b)x
x² – 4ax + 4a² – b² = x² – (2a + b)x – (2a – b)x + (2a + b)(2a – b) = 0
⇒ x (x – 2a – b) – (2a – b)(x – 2a – b) = 0
⇒ (x – 2a – b)(x – 2a + b)
Either, x – 2a – b = 0, then x = 2a + b
or x – 2a + b = 0, then x = 2a – b
Hence, x = (2a + b) or (2a – b)

Hope given RS Aggarwal Solutions Class 10 Chapter 10 Quadratic Equations Test Yourself are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.