RS Aggarwal Class 10 Solutions Chapter 2 Polynomials MCQS
These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Class 10 Solutions Chapter 2 Polynomials MCQS
Other Exercises
- RS Aggarwal Solutions Class 10 Chapter 2 Polynomials Ex 2A
- RS Aggarwal Solutions Class 10 Chapter 2 Polynomials Ex 2B
- RS Aggarwal Solutions Class 10 Chapter 2 Polynomials Ex 2C
- RS Aggarwal Solutions Class 10 Chapter 2 Polynomials MCQS
- RS Aggarwal Solutions Class 10 Chapter 2 Polynomials Test Yourself
Choose the correct answer in each of the following questions.
Question 1.
Solution:
(d) √2 x2 – 3√3 x + √6 is polynomial, others are not polynomial.
Question 2.
Solution:
(d) x + \(\frac { 3 }{ x }\) is not a polynomial, other are polynomial.
Question 3.
Solution:
(c) Let f(x) = x2 – 2x – 3
= x2 – 3x + x – 3
= x(x – 3) + 1(x – 3)
= (x – 3)(x + 1)
If x – 3 = 0, then x – 3
and if x + 1 = 0, then x = -1
Zeros are 3, -1
Question 4.
Solution:
(b)
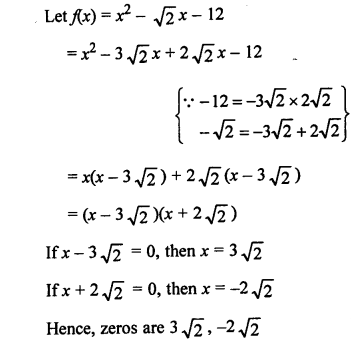
Question 5.
Solution:
(c)
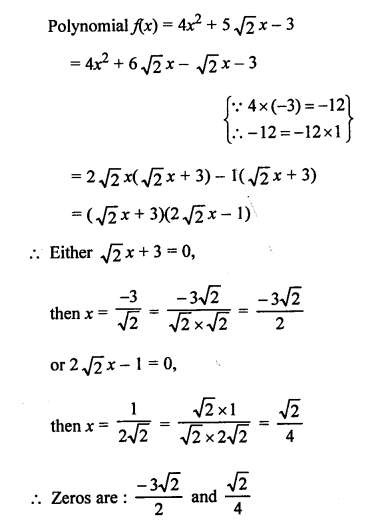
Question 6.
Solution:
(b) Polynomial is x2 + \(\frac { 1 }{ 6 }\) x – 2
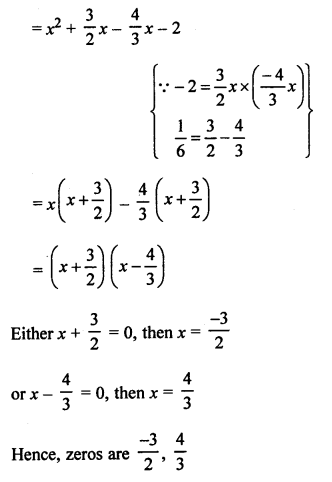
Question 7.
Solution:
(a)
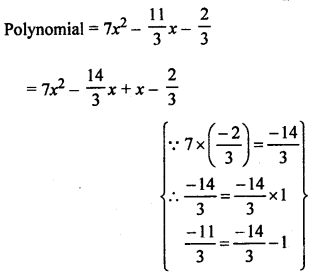
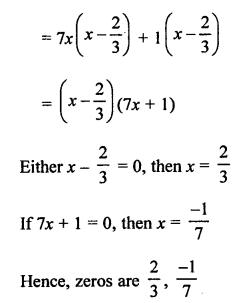
Question 8.
Solution:
(c) Sum of zeros = 3
Product of zeros = -10
Polynomial : x2 – (Sum of zeros) x + Product of zeros
= x2 – 3x – 10
Question 9.
Solution:
(c) Zeros are 5 and -3
Sum of zeros = 5 – 3 = 2
Product of zeros = 5 x (-3) = -15
Polynomial: x2 – (Sum of zeros) x + Product of zeros
= x2 – 2x – 15
Question 10.
Solution:
(d)

Question 11.
Solution:
(b) Let f(x) = x2 + 88x +125
Here, sum of roots = \(\frac { -b }{ a }\) = -88
and product = \(\frac { c }{ a }\) = 125
Product is positive,
Both zeros can be both positive or both negative.
Sum is negative.
Both zeros are negative.
Question 12.
Solution:
(b) α and β are the zeros of x2 + 5x + 8
Then sum of zeros (α + β) = \(\frac { -b }{ a }\) = \(\frac { -5 }{ 1 }\) = -5
Question 13.
Solution:
(c) α and β are the zeros of 2x2 + 5x – 9
Product of zeros (αβ) = \(\frac { c }{ a }\) = \(\frac { -9 }{ 2 }\)
Question 14.
Solution:
(d) 2 is a zero of kx2 + 3x + k
It will satisfy the quadratic equation kx2 + 3x + k = 0
k(2)2 + 3x2 + 1 = 0
4k + 6 + k = 0
=> 5k = -6
k = \(\frac { -6 }{ 5 }\)
Question 15.
Solution:
(b) -4 is a zero of (k – 1) x2 + 4x + 1
-4 will satisfy the equation (k – 1) x2 + kx + 1 = 0
=> (k – 1)(-4)2 + k(-4) + 1 =0
=> 16k – 16 – 4k + 1 = 0
=> 12k – 15 = 0
=> 12k = 15
=> k = \(\frac { 15 }{ 12 }\) = \(\frac { 5 }{ 4 }\)
Question 16.
Solution:
(c)

Question 17.
Solution:
(a)

Question 18.
Solution:
(d) Polynomial: kx2 + 2x + 3k
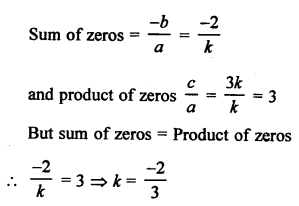
Question 19.
Solution:
(b) α, β are the zeros of the polynomial x2 + 6x + 2
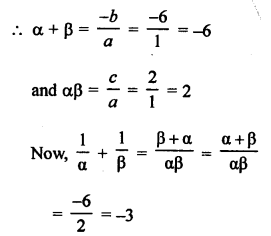
Question 20.
Solution:
(a) α, β, γ are the zeros of x3 – 6x2 – x + 30
Then αβ + βγ + γα = \(\frac { c }{ a }\) = \(\frac { -1 }{ 1 }\) = -1
Question 21.
Solution:
(a) α, β, γ are the zeros of 2x3 + x2 – 13x + 6, then
αβγ = \(\frac { -d }{ a }\) = \(\frac { -6 }{ 2 }\) = -3
Question 22.
Solution:
(c) α, β, γ are the zeros of p(x) such that
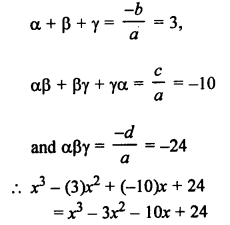
Question 23.
Solution:
(a)
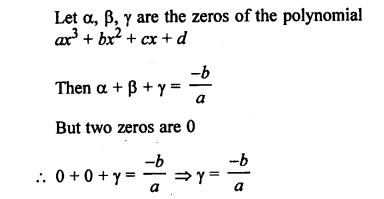
Question 24.
Solution:
(b) If one zero of cubic polynomial ax3 + bx2 + cx + d = 0
Let a be zero, then
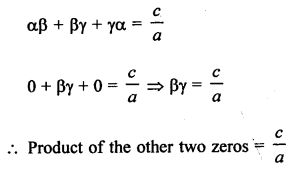
Question 25.
Solution:
(c)

Question 26.
Solution:
(d)
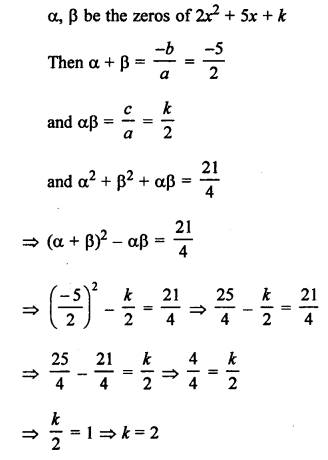
Question 27.
Solution:
(c) p(x) is divided by q(x), then
p(x) = q(x) x g(x) + r(x)
Either r(x) = 0
Degree of r(x) < deg of g(x)
Question 28.
Solution:
(d) (a) is not a linear polynomial.
(b) is trinomial not binomial.
(c) is not a monomial.
(d) 5x2 is monomial is true.
Hope given RS Aggarwal Solutions Class 10 Chapter 2 Polynomials MCQS are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.