RS Aggarwal Class 10 Solutions Chapter 3 Linear equations in two variables Ex 3A
These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 3 Linear equations in two variables Ex 3A.
RS Aggarwal Solutions Class 10 Chapter 3
- RS Aggarwal Solutions Class 10 Chapter 3 Linear equations in two variables Ex 3A
- RS Aggarwal Solutions Class 10 Chapter 3 Linear equations in two variables Ex 3B
- RS Aggarwal Solutions Class 10 Chapter 3 Linear equations in two variables Ex 3C
- RS Aggarwal Solutions Class 10 Chapter 3 Linear equations in two variables Ex 3D
- RS Aggarwal Solutions Class 10 Chapter 3 Linear equations in two variables Ex 3E
- RS Aggarwal Solutions Class 10 Chapter 3 Linear equations in two variables Ex 3F
- RS Aggarwal Solutions Class 10 Chapter 3 Linear equations in two variables MCQS
- RS Aggarwal Solutions Class 10 Chapter 3 Linear equations in two variables Test Yourself
Solve each of the following systems of equations graphically.
Question 1.
Solution:
2x + 3y = 2 …..(i)
x – 2y = 8 …(ii)
From Eq. (i),
⇒ 2x = 2 – 3y
⇒x = \(\frac { 2 – 3y }{ 2 }\)
Giving some different values to y, we get corresponding values of x as given below:
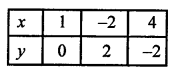
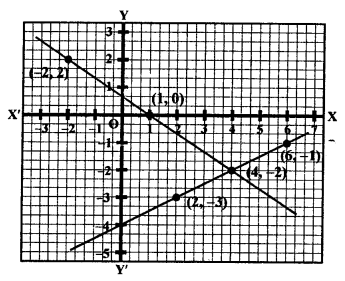
Now, plot the points (1, 0), (-2, 2) and (4, -2) on the graph and join them to get a line.
Similarly x – 2y = 8 ⇒ x = 8 + 2y
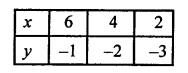
Now plot the points (6, -1), (4, -2) and (2, -3) on the graph and join them to get another line.
We see that these two lines intersect each other at point(4, -2).
x = 4, y = -2
Question 2.
Solution:
3x + 2y = 4
⇒ 3x = 4 – 2y
⇒ x = \(\frac { 4 – 2y }{ 3 }\)
Giving some different values to y, we get corresponding values of x as given below:
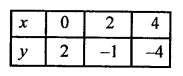
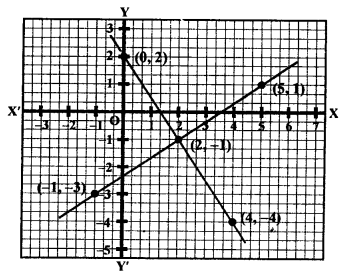
Now plot the points (0, 2), (2, -1) and (4, -4) on the graph and join them to get a line. Similarly,
2x – 3y = 7
2x = 3y+ 7
x = \(\frac { 3y+ 7 }{ 2 }\)
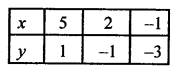
Now plot the points on the graph and join them to get another line.
We see that these two lines intersect each other at point (2, -1).
x = 2, y = -1
Question 3.
Solution:
2x + 3y = 8
⇒ 2x = 8 – 3y
x = \(\frac { 8 – 3y }{ 2 }\)
Now, giving some different values to y, we get corresponding values of x as given below
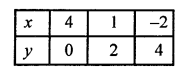
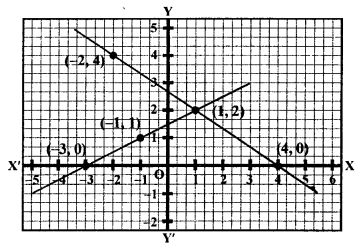
Now, we plot the points (4,0), (2,3) and (0, 6) on the graph and join them to get a line.
Similarly,
x – 2y + 3 = 0
x = 2y – 3
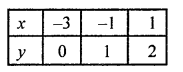
Now, plot the points (-3, 0), (-1, 1) and (1, 2) on the graph and join them to get another line.
We see that these two lines intersect each other at the point (1, 2).
x = 1, y = 2
Question 4.
Solution:
2x – 5y + 4 = 0
⇒ 2x = 5y – 4
x = \(\frac { 5y – 4 }{ 2 }\)
Giving some different values to y, we get corresponding values of x as given below:
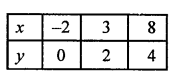
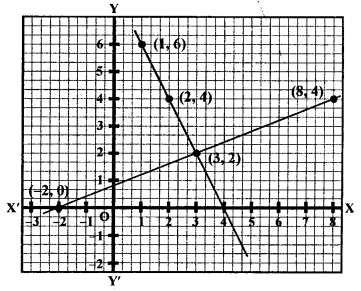
Now, plot the points (-2, 0) (3, 2) and (8,4) on the graph and join them to get a line.
Similarly,
2x + y – 8 = 0
⇒ y = 8 – 2x
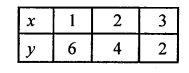
Plot the points (1, 6), (2, 1) and (3, 2) on the graph and join them to get another line.
We see that these two lines intersect each other at the point (3, 2).
x = 3, y = 2
Question 5.
Solution:
3x + 2y = 12
⇒ 3x = 12 – 2y
x = \(\frac { 12 – 2y }{ 2 }\)
Giving some different values to y, we get corresponding the values of x as given below:
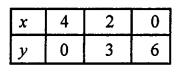
Now, we plot the points (4,0), (2,3) and (0, 6) on the graph and join them to get a line.
Similarly,
5x – 2y = 4
⇒ 5x = 4 + 2 y
⇒ x = \(\frac { 4 + 2 y }{ 5 }\)
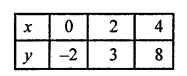
Plot the points (0, -2), (2, 3) and (4, 8) on the graph and join them to get another line.
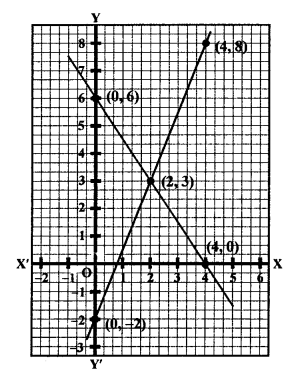
We see that these two lines intersect each other at the point (2, 3).
x = 2, y = 3
Question 6.
Solution:
3x + y + 1 = 0 ⇒y = -3x – 1
Giving some different values to x, we get corresponding values of y as given below:
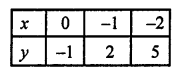
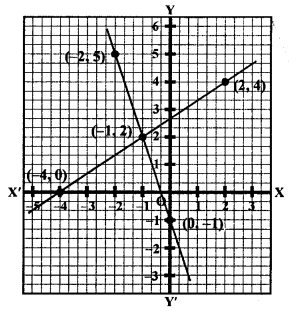
Now, plot the points (0, -1), (-1, 2) and (-2, 5) on the graph and join them to get a line.
Similarly,
2x – 3y + 8 = 0
2x = 3y – 8
x = \(\frac { 3y – 8 }{ 2 }\)
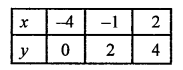
Now, plot the points (-4, 0), (-1, 2) and (2, 4) on the graph and join them to get another line.
We see that these two lines intersect each other at the points (-1, 2).
x = -1, y = 2
Question 7.
Solution:
2x + 3y + 5 = 0
2x = -3y – 5
x = \(\frac { -3y – 5 }{ 2 }\)
Giving some different values to y, we get corresponding values of x as given below:
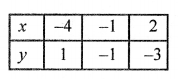
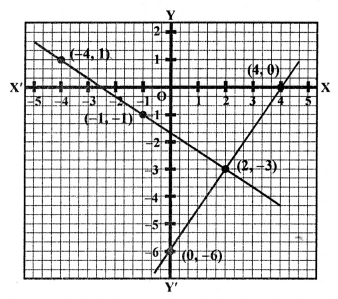
Now, plot the points (-4, 1), (-1, -1) and (2, -3) on the graph and join them to get a line. Similarly,
3x – 2y – 12 = 0
⇒ 3x = 2y + 12
x = \(\frac { 2y + 12 }{ 3 }\)
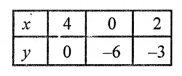
Plot the points (4, 0), (0, -6) and (2, -3) on the graph and join them to get another line.
We see that these two lines intersect each other at the point (2, -3).
x = 2, y = -3
Question 8.
Solution:
2x – 3y + 13 = 0
⇒ 2x = 3y – 13
⇒ x = \(\frac { 3y – 13 }{ 2 }\)
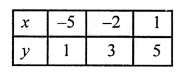
Giving some different values to y, we get corresponding values of x as given below:
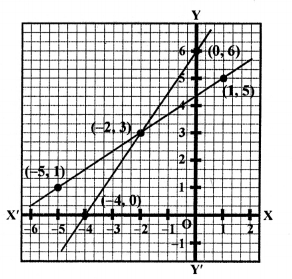
Now, plot the points (-5, 1), (-2, 3) and (1, 5) on the graph and join them to get a line.
Similarly,
3x – 2y + 12 = 0
3x = 2y – 12
x = \(\frac { 2y – 12 }{ 3 }\)
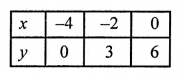
Now, plot the points (-4, 0), (-2, 3) and (0, 6) on the graph and join them to get another line.
We see that these lines intersect each other at the point (-2, 3).
x = -2, y = 3
Question 9.
Solution:
2x + 3y – 4 = 0
⇒ 2x = 4 – 3y
⇒ x = \(\frac { 4 – 3y }{ 2 }\)
Giving some different values to y, we get corresponding values of x as given below:
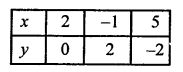
Plot the points (2, 0) (-1, 2) and (5, -2) on the graph and join them to get a line.
Similarly,
3x – y + 5 = 0
⇒ -y = -5 – 3x
⇒ y = 5 + 3x
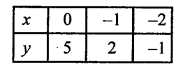
Plot the points (0, 5), (-1, 2) and (-2, -1) on the graph and join them to get another line.
We see that these two lines intersect each other at the point (-1, 2).
x = -1, y = 2
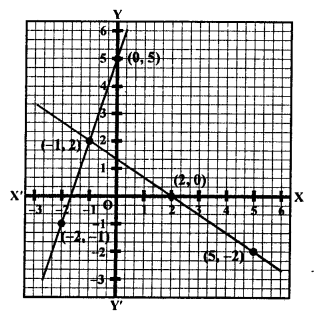
Question 10.
Solution:
x + 2y + 2 = 0
⇒ x = – (2y + 2)
Giving some different values to y, we get corresponding the values of x as given below:
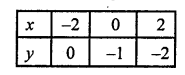
Plot the points (-2,0), (0, -1) and (2, -2) on the graph and join them to get a line.
Similarly,
3x + 2y – 2 = 0
⇒ 3x = 2 – 2y
x = \(\frac { 2 – 2y }{ 3 }\)
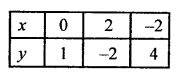
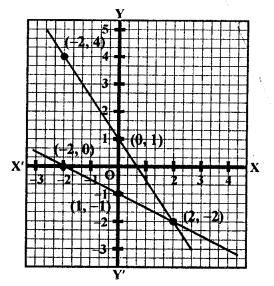
Plot the points (0, 1), (2, -2) and (-2, 4) on the graph and join them to get another line.
We see that these two lines intersect each other at the point (2, -2).
x = 2, y = -2
Solve each of the following given systems of equations graphically and find the vertices and area of the triangle formed by these lines and the x-axis:
Question 11.
Solution:
x – y + 3 = 0
⇒ x = y – 3
Giving some different value to y, we get corresponding values of x as given below:
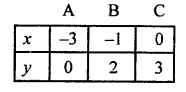
Plot the points (-3, 0), (-1, 2) and (0, 3) on the graph and join them to get a line.
Similarly,
2x + 3y – 4 = 0
⇒ 2x = 4 – 3y
x = \(\frac { 4 – 3y }{ 2 }\)
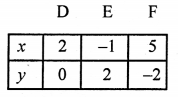
Plot the points (2, 0), (-1, 2) and (5, -2) on the graph and join them to get another line.
We see that these line intersect each other at (-1, 2) and x-axis at A (-3, 0) and D (2, 0).
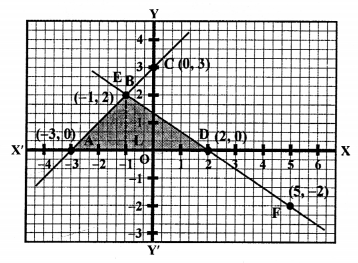
Area of ∆BAD = \(\frac { 1 }{ 2 }\) x base x altitude
= \(\frac { 1 }{ 2 }\) x AD x BL
= \(\frac { 1 }{ 2 }\) x 5 x 2 = 5 sq.units
Question 12.
Solution:
2x – 3y + 4 = 0
⇒ 2x = 3y – 4
x = \(\frac { 3y – 4 }{ 2 }\)
Giving some different values to y, we get corresponding value of x as given below:
Plot the points (-2, 0), (1, 2) and (4, 4) on the graph and join them to get a line.
Similarly,
x + 2y – 5 = 0
x = 5 – 2y
Now, plot the points (5, 0), (3, 1) and (1, 2) on the graph and join them to get another line.
We see that there two lines intersect each other at the point B (1, 2) and intersect x- axis at A (-2, 0) and D (5, 0) respectively.
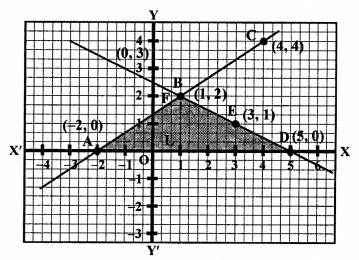
Now, area of ∆BAD = \(\frac { 1 }{ 2 }\) x base x altitude
= \(\frac { 1 }{ 2 }\) x AD x BL
= \(\frac { 1 }{ 2 }\) x 7 x 2
= 7 sq. units
Question 13.
Solution:
4x – 3y + 4 = 0
⇒ 4x = 3y – 4
x = \(\frac { 3y – 4 }{ 4 }\)
Giving some different values to y, we get corresponding value of x as given below:
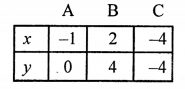
Plot the points (-1, 0), (2, 4) and (-4, -4) on the graph and join them, to get a line.
Similarly,
4x + 3y – 20 = 0
4x = 20 – 3y
x = \(\frac { 20 – 3y }{ 4 }\)
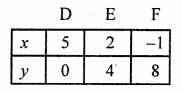
Plot the points (5, 0), (2, 4) and (-1, 8) on the graph and join them to get a line.
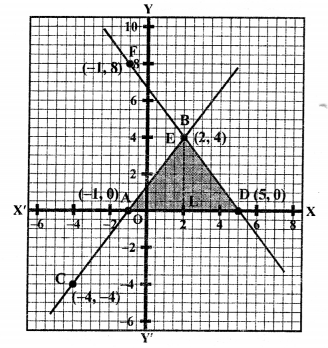
We see that these two lines intersect each other at the point B (2, 4) and intersect x-axis at A (-1, 0) and D (5, 0).
Area ∆BAD = \(\frac { 1 }{ 2 }\) x base x altitude
= \(\frac { 1 }{ 2 }\) x AD x BL
= \(\frac { 1 }{ 2 }\) x 6 x 4 = 12 sq. units
Question 14.
Solution:
x – y + 1 = 0 ⇒ x = y – 1
Giving some different values toy, we get the values of x as given below:
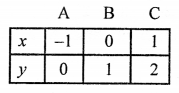
Plot the points (-1, 0), (0, 1) and (1, 2) on the graph and join them to get a line.
Similarly,
3x + 2y – 12 = 0
⇒ 3x = 12 – 2y
x = \(\frac { 12 – 2y }{ 3 }\)
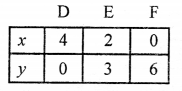
Plot the points (4, 0), (2, 3) and (0, 6) on the graph and join them to get another line.
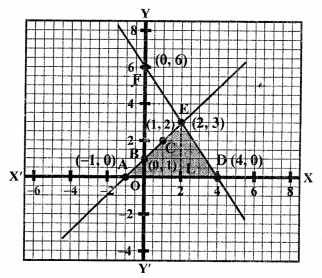
We see that these two lines intersect each ohter at the point E (2, 3) and intersect x- axis at A (-1, 0) and D (4, 0).
Area of ∆EAD = \(\frac { 1 }{ 2 }\) x base x altitude 1
= \(\frac { 1 }{ 2 }\) x AD x EL
= \(\frac { 1 }{ 2 }\) x 5 x 3
= \(\frac { 15 }{ 2 }\)
= 7.5 sq. units
Question 15.
Solution:
x – 2y + 2 = 0 ⇒ x = 2y – 2
Giving some different values to y, we get corresponding values of x as given below:
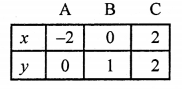
Plot the points (-2, 0), (0, 1), (2, 2) on the graph and join them to get a line.
Similarly,
2x + y – 6 = 0
⇒ y = 6 – 2x
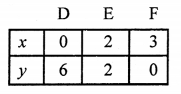
Plot the points on the graph and join them to get a line.
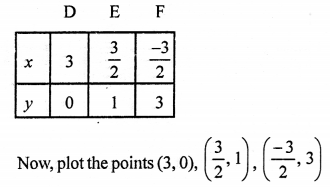
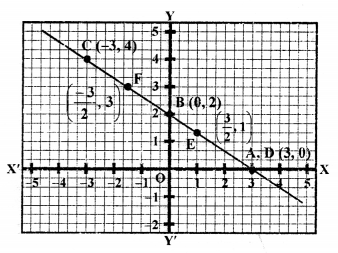
We see that these two lines intersect each other at the point C (2, 2) and intersect the x-axis at A (-2, 0) and F (3, 0).
Now, area of ∆CAF = \(\frac { 1 }{ 2 }\) x base x altitude
= \(\frac { 1 }{ 2 }\) x AF x CL
= \(\frac { 1 }{ 2 }\) x 5 x 2 = 5 sq. units
Solve each of the following given systems of equations graphically and find the vertices and area of the triangle formed by these lines and the y-axis:
Question 16.
Solution:
2x – 3y + 6 = 0
⇒ 2x = 3y – 6
x = \(\frac { 3y – 6 }{ 2 }\)
Giving some different values to y, we get corresponding values of x, as given below:
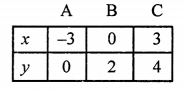
Now, plot the points (-3, 0), (0, 2), (3, 4) on the graph and join them to get a line.
Similarly,
2x + 3y – 18 = 0
2x = 18 – 3y
x = \(\frac { 18 – 3y }{ 2 }\)
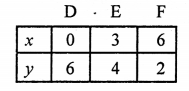
Plot the points (0, 6), (3, 4) and (6, 2) on the graph and join them to get a line.
We see that these two lines intersect each other at C (3, 4) and intersect y-axis at B (0, 2) and D (0, 6).
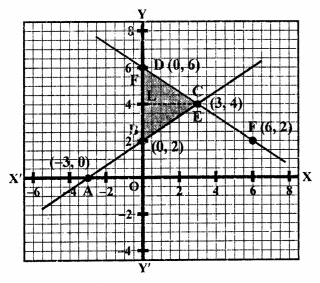
Now, area of ∆CBD = \(\frac { 1 }{ 2 }\) x base x altitude
= \(\frac { 1 }{ 2 }\) x BD x CL
= \(\frac { 1 }{ 2 }\) x 4 x 3 sq. units = 6 sq. units
Question 17.
Solution:
4x – y – 4 = 0
⇒ 4x = y + 4
x = \(\frac { y + 4 }{ 2 }\)
Giving some different values to y, we get corresponding values of x as given below:
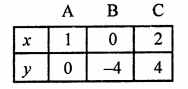
Plot the points (1, 0), (0, -4) and (2, 4) on the graph and join them to get a line.
Similarly,
3x + 2y – 14 = 0
2y = 14 – 3x
y = \(\frac { 14 – 3x }{ 2 }\)
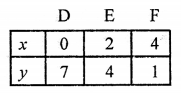
Now, plot the points (0, 7), (2, 4) and (4, 1) on the graph and join them to get another line.
We see that these two lines intersect each other at C (2, 4) and y-axis at B (0, -4) and D (0, 7) respectively.
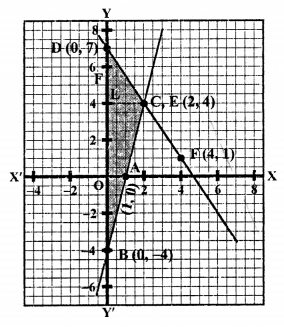
Area of ∆CBD = \(\frac { 1 }{ 2 }\) x base x altitude
= \(\frac { 1 }{ 2 }\) x BD x CL
= \(\frac { 1 }{ 2 }\) x 11 x 2 sq. units = 11 sq. units
Question 18.
Solution:
x – y – 5 = 0 ⇒ x = y + 5
Giving some different values to y, we get corresponding values of x as given below:
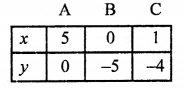
Plot the points (5, 0), (0, -5) and (1, -4) on the graph and join these to get a line.
Similarly,
3x + 5y – 15 = 0
3x = 15 – 5y
x = \(\frac { 15 – 5y }{ 3 }\)
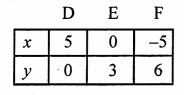
Plot the points (5, 0), (0, 3) and (-5, 6) on the graph and join them to get a line.
We see that these two lines intersect each other at A (5, 0) and y-axis at B (0, -5) and E (0, 3) respectively.
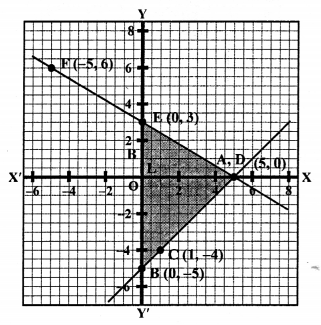
Now area of ∆ABE = \(\frac { 1 }{ 2 }\) x base x altitude
= \(\frac { 1 }{ 2 }\) x BE x AL
= \(\frac { 1 }{ 2 }\) x 8 x 5 sq. units = 20 sq. units
Question 19.
Solution:
2x – 5y + 4 = 0
⇒ 2x = 5y – 4
x = \(\frac { 5y – 4 }{ 2 }\)
Giving some different values to y, we get corresponding values of x as given below:
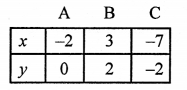
Plot the points (-2, 0), (3, 2) and (-7, -2) on the graph and join them to get a line.
Similarly,
2x + y – 8 = 0
2x = 8 – y
x = \(\frac { 8 – y }{ 2 }\)
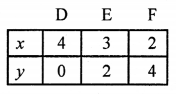
Plot the points (4, 0), (3, 2) and (2, 4) on the graph and join them to get a line.
We see that these two lines intersect each other at B (3, 2) and y-axis at G (0, 1) and H (0, 8) respectively.
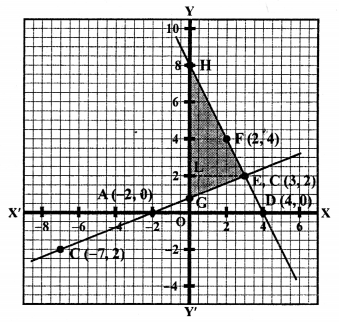
Now area of ∆EGH = \(\frac { 1 }{ 2 }\) x base x altitude
= \(\frac { 1 }{ 2 }\) x GH x EL
= \(\frac { 1 }{ 2 }\) x 7 x 3 sq. units
= \(\frac { 21 }{ 2 }\) = 10.5 sq. units
Question 20.
Solution:
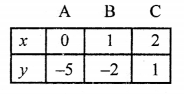
5x – y – 7 = 0 ⇒ y = 5x – 7
Giving some different values to x, we get corresponding values of y as given below:
Plot the points (0, -7), (1, -2), (2, 3) on the graph and join them to get a line.
Similarly,
x – y + 1 = 0 ⇒ x = y – 1
Plot the points (-1, 0), (1, 2) and (2, 3) on the graph and join them to get a line.
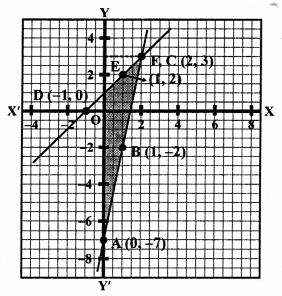
We see that these two lines intersect each other at C (2, 3) and intersect y-axis at A (0, -7) and F (0, 1) respectively.
Now, area of ∆CAF = \(\frac { 1 }{ 2 }\) x base x altitude
= \(\frac { 1 }{ 2 }\) x AF x CL
= \(\frac { 1 }{ 2 }\) x 8 x 2 = 8 sq.units
Question 21.
Solution:
2x – 3y – 12 ⇒ 2x = 12 + 3y
x = \(\frac { 12 + 3y }{ 2 }\)
Giving some different values to y, we get corresponding values of x as given below:
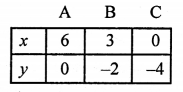
Plot the points (6, 0), (3, -2) and (0, -4) on the graph and join them to get a line.
Similarly,
x + 3y = 6 ⇒ x = 6 – 3y
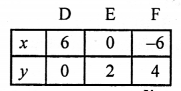
Plot the points (6, 0), (0, 2) and (-6, 4) on the graph and join them to get a line.
We see that these two lines intersect each other at the points A (6, 0) and intersect the y-axis at C (0, -4) and E (0, 2) respectively.
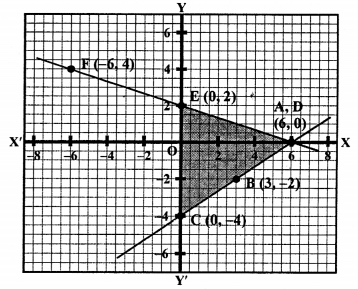
Now area of ∆ACE = \(\frac { 1 }{ 2 }\) x base x altitude
= \(\frac { 1 }{ 2 }\) x CE x AO
= \(\frac { 1 }{ 2 }\) x 6 x 6 sq. units = 18 sq.units
Show graphically that each of the following given systems of equations has infinitely many solutions:
Question 22.
Solution:
2x + 3y = 6
2x = 6 – 3y
x = \(\frac { 6 – 3y }{ 2 }\)
Giving some different values to y, we get the corresponding val ues of x as given below:
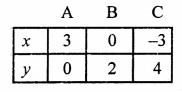
Plot the points (3, 0), (0, 2) and (-3, 4) on the graph and join them to get a line.
Similarly,
4x + 6y = 12
4x = 12 – 6y
x = \(\frac { 12 – 6y }{ 2 }\)
on the graph and join them to get a line.
We see that all the points lie on the same straight line.
This system has infinite many solutions.
Question 23.
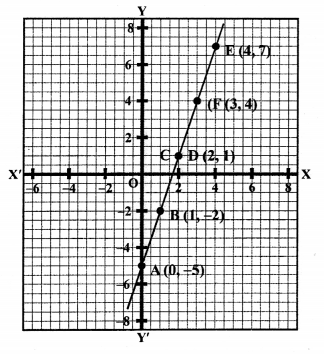
Solution:
3x – y = 5
⇒ y = 3x – 5
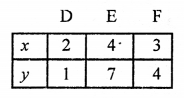
Giving some different values to x, we get corresponding values of y as shown below:
Now, plot the points (0, -5), (1, -2), (2, 1) on the graph and join them to get a line:
Similarly,
6x – 2y = 10
⇒ 6x = 10 + 2y
x = \(\frac { 10 + 2y }{ 6 }\)
Plot the points (2, 1), (4, 7), (3, 4) on the graph and join them to get another line.
We see that these lines coincide each other.
This system has infinite many solutions.
Question 24.
Solution:
2x + y = 6
y = 6 – 2x
Giving some different values to x, we get corresponding values of y as given below:
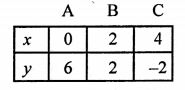
Plot the points (0, 6), (2, 2), (4, -2) on the graph and join them to get a line.
Similarly,
6x + 3y = 18
⇒ 6x = 18 – 3y
⇒ x = \(\frac { 18 – 3y }{ 2 }\)
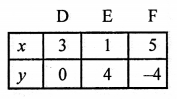
Now, plot the points (3, 0), (1, 4) and (5, -4) on the graph and join them to get another line.
We see that these two lines coincide each other.
This system has infinitely many solutions
Question 25.
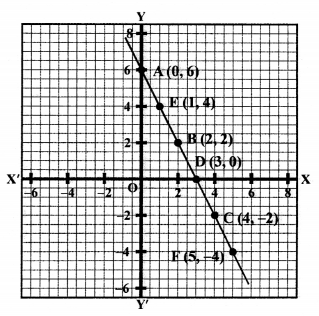
Solution:
x – 2y = 5 ⇒ x = 5 + 2y
Giving some different values to y, we get corresponding values of x as shown below:
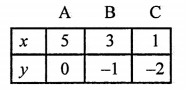
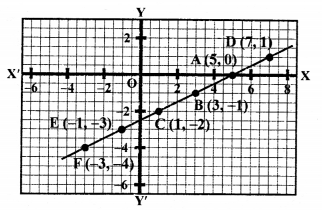
Plot the points (5, 0), (3, -1), (1, -2) on the graph and join them to get a line.
similarly,
3x – 6y = 15
⇒ 3x = 15 + 6y
x = \(\frac { 15 + 6y }{ 3 }\)
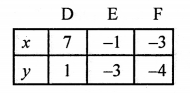
Plot the points (7, 1), (-1, -3) and (-3, -4) on the graph and join them to get another line.
We see that all the points lie on the same line.
Lines coincide each other.
Hence, the system has infinite many solutions.
Show graphically that each of the following given systems of equations is inconsistent, i.e., has no solution:
Question 26.
Solution:
x – 2y = 6 ⇒ x = 6 + 2y
Giving some different values to y, we get corresponding values of x as given below:
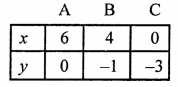
Plot the points (6, 0), (4, -1) and (0, -3) on the graph and join them to get a line.
Similarly,
3x – 6y = 0
⇒ 3x = 6y
⇒ x = 2y
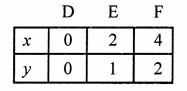
Plot the points (0, 0), (2, 1), (4, 2) on the graph and join them to get a line.
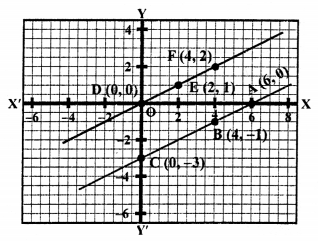
We see that these two lines are parallel i.e., do not intersect each other.
This system has no solution.
Question 27.
Solution:
2x + 3y = 4
⇒ 2x = 4 – 3y
⇒ x = \(\frac { 4 – 3y }{ 2 }\)
Giving some different values to y, we get corresponding values of x as given below:
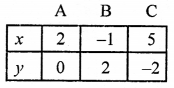
Plot the points (2, 0), (-1, 2) and (5, -2) on the graph and join them to get a line.
Similarly,
4x + 6y = 12 ⇒ 4x = 12 – 6y
x = \(\frac { 12 – 6y }{ 4 }\)
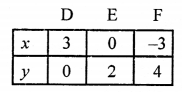
Plot the points (3, 0), (0, 2) and (-3, 4) on the graph and join them to get another line.
We see that two lines are parallel i.e., these do not intersect each other at any point.
Therefore the system has no solution.
Question 28.
Solution:
2x + y = 6, y = 6 – 2x
Giving some different values to x, we get corresponding values ofy as given below:
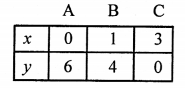
Plot the points (0, 6), (1, 4) and (3, 0) on the graph and join them to get a line.
Similarly,
6x + 3y = 20 ⇒ 6x = 20 – 3y
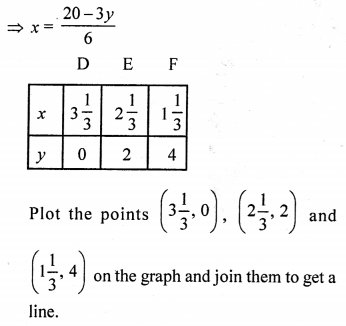
We see that these two lines are parallel and do not intersect each other.
Therefore this system has no solution.
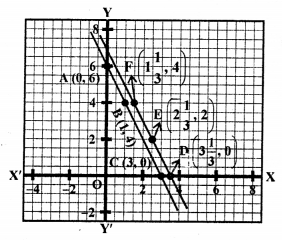
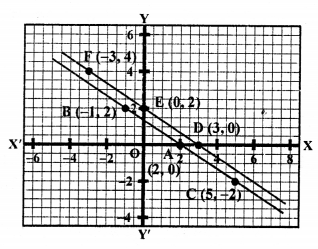
Question 29.
Solution:
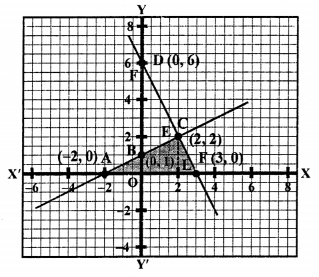
2x + y = 2 ⇒ y = 2 – 2x
Giving some different values to x, we get corresponding values of y as given below:
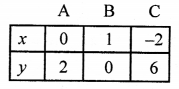
Plot the points (0, 2), (1, 0) and (-2, 6) on the graph and join them to get a line.
Similarly,
2x + y = 6 ⇒ y = 6 – 2x
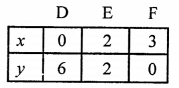
Plot the points (0, 6), (2, 2) and (3, 0) on the graph and join them to get another line.
ABFD is the trapezium whose vertices are A (0, 2), B (1, 0), F (3, 0), D (0, 6).
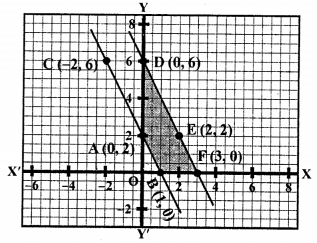
Area of trapezium ABFD = Area ∆DOF – Area ∆AOB
= \(\frac { 1 }{ 2 }\) (DO x OF) – \(\frac { 1 }{ 2 }\) (AO x OB)
= \(\frac { 1 }{ 2 }\) (6 x 3) – \(\frac { 1 }{ 2 }\) (2 x 1) sq.units
= 9 – 1 = 8 sq.units
Hope given RS Aggarwal Solutions Class 10 Chapter 3 Linear equations in two variables Ex 3A are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.