RS Aggarwal Class 10 Solutions Chapter 3 Linear equations in two variables Test Yourself

RS Aggarwal Class 10 Solutions Chapter 3 Linear equations in two variables Test Yourself

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 3 Linear equations in two variables Test Yourself.

RS Aggarwal Solutions Class 10 Chapter 3

• RS Aggarwal Solutions Class 10 Chapter 3 Linear equations in two variables Ex 3A
• RS Aggarwal Solutions Class 10 Chapter 3 Linear equations in two variables Ex 3B
• RS Aggarwal Solutions Class 10 Chapter 3 Linear equations in two variables Ex 3C
• RS Aggarwal Solutions Class 10 Chapter 3 Linear equations in two variables Ex 3D
• RS Aggarwal Solutions Class 10 Chapter 3 Linear equations in two variables Ex 3E
• RS Aggarwal Solutions Class 10 Chapter 3 Linear equations in two variables Ex 3F
• RS Aggarwal Solutions Class 10 Chapter 3 Linear equations in two variables MCQS
• RS Aggarwal Solutions Class 10 Chapter 3 Linear equations in two variables Test Yourself

MCQ
Question 1.
Solution:
(a)

Question 2.
Solution:
(d)

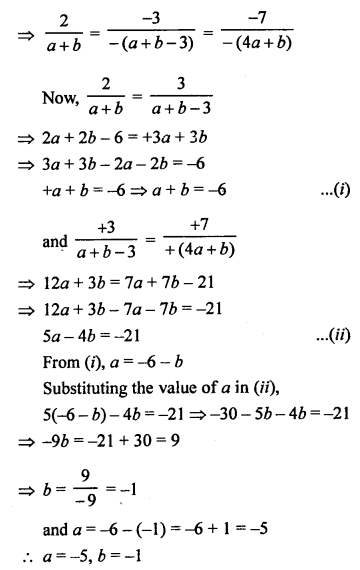
Question 3.
Solution:
(a)

Question 4.
Solution:
(d)

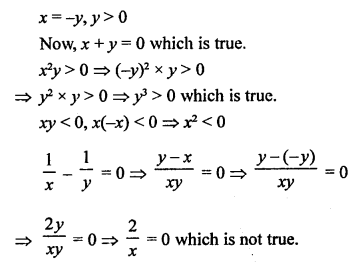
Short-Answer Questions
Question 5.
Solution:

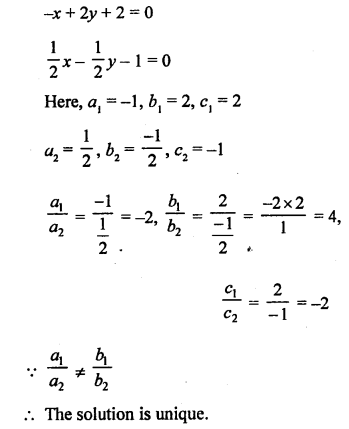
Question 6.
Solution:

Question 7.
Solution:

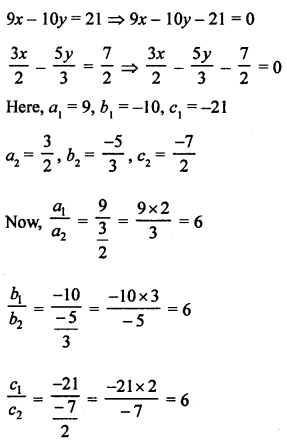
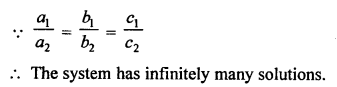
Question 8.
Solution:

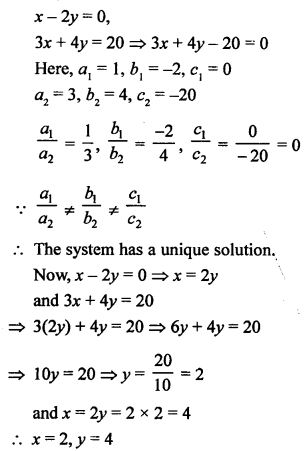
Question 9.
Solution:

Question 10.
Solution:
Let first number = x
and second number = y
According to the conditions, x – y = 26 …(i)
and x = 3y …..(ii)
From (i),
3y – y = 26
⇒ 2y = 26
⇒ y = 13
and x = 3 x 13 = 39
Numbers are 39 and 13

Short-Answer Questions (3 marks)
Question 11.
Solution:
23x + 29y = 98 …..(i)
29x + 23y = 110 …..(ii)
Adding, we get 52x + 52y = 208
x + y = 4 …..(iii) (Dividing by 52)
and subtracting,
-6x + 6y = -12
x – y = 2. …..(iv) (Dividing by -6)
Adding (iii) and (iv),
2x = 6 ⇒ x = 3
Subtracting,
2x = 2 ⇒ y = 1
Hence, x = 3, y = 1

Question 12.
Solution:


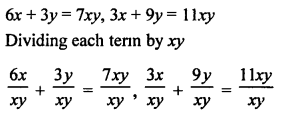
x = 1, y = \(\frac { 3 }{ 2 }\)

Question 13.
Solution:

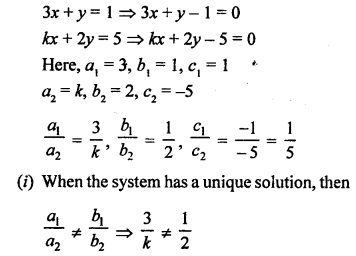
Question 14.
Solution:

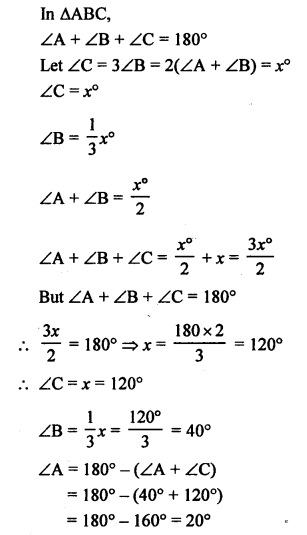
Question 15.
Solution:
Let cost of one pencil = ₹ x
and cost of one pen = ₹ y
According to the condition,
5x + 7y = 195 …(i)
7x + 5y= 153 …(ii)
Adding, (i) and (ii)
12x + 12y = 348
x + y = 29 ….(iii) (Dividing by 12)
and subtracting,
-2x + 2y = 42
-x + y = 21 …..(iv) (Dividing by -2)
Now, Adding (iii) and (iv),
2y = 50 ⇒ y = 25
and from (iv),
-x + 25 = 21 ⇒ -x = 21 – 25 = -4
x = 4
Cost of one pencil = ₹ 4
and cost of one pen = ₹ 25

Question 16.
Solution:
2x – 3y = 1, 4x – 3y + 1 = 0
2x – 3y = 1
2x = 1 + 3y
x = \(\frac { 1 + 3y }{ 2 }\)
Giving some different values to y, we get corresponding values of x as given below

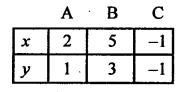
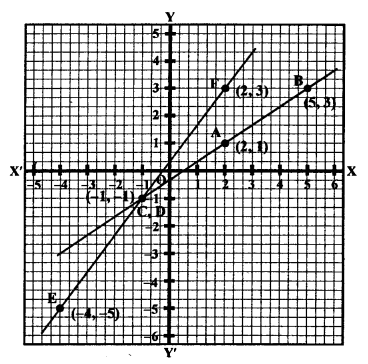
Now plot the points (2, 1), (5, 3) and (-1, -1) on the graph and join them to get a line.
Similarly,
4x – 3y + 1 = 0
⇒ 4x = 3y – 1
⇒ x = \(\frac { 3y – 1 }{ 4 }\)

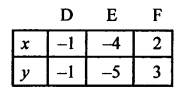
Now plot the points (-1, -1), (-4, -5) and (2, 3) on the graph and join them to get another line which intersects the first line at the point (-1, -1).
Hence, x = -1, y = -1

Long-Answer Questions
Question 17.
Solution:
We know that opposite angles of a cyclic quadrilateral are supplementary.
∠A + ∠C = 180° and ∠B + ∠D = 180°
Now, ∠A = 4x° + 20°, ∠B = 3x° – 5°, ∠C = 4y° and ∠D = 7y° + 5°
But ∠A + ∠C = 180°
4x + 20° + 4y° = 180°
⇒ 4x + 4y = 180° – 20 = 160°
x + y = 40° …(i) (Dividing by 4)
and ∠B + ∠D = 180°
⇒ 3x – 5 + 7y + 5 = 180°
⇒ 3x + 7y = 180° …(ii)
From (i), x = 40° – y
Substituting the value of x in (ii),
3(40° – y) + 7y = 180°
⇒ 120° – 3y + 7y = 180°
⇒ 4y = 180°- 120° = 60°
y = 15°
and x = 40° – y = 40° – 15° = 25°
∠A = 4x + 20 = 4 x 25 + 20 = 100 + 20= 120°
∠B = 3x – 5 = 3 x 25 – 5 = 75 – 5 = 70°
∠C = 4y = 4 x 15 = 60°
∠D = 7y + 5 = 7 x 15 + 5 = 105 + 5 = 110°

Question 18.
Solution:

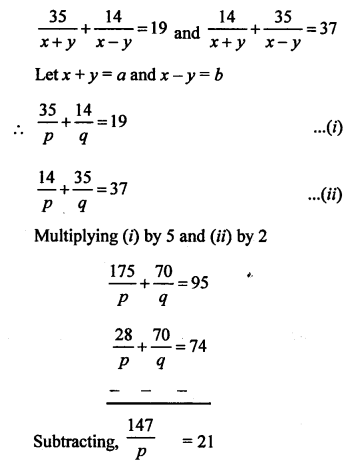
Question 19.
Solution:
Let numerator of a fraction = x
and denominator = y
Fraction = \(\frac { x }{ y }\)
According to the conditions,

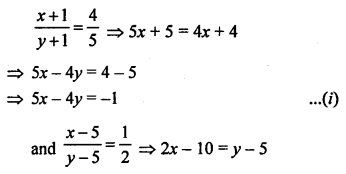
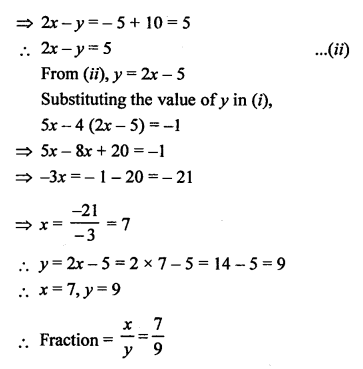
Question 20.
Solution:

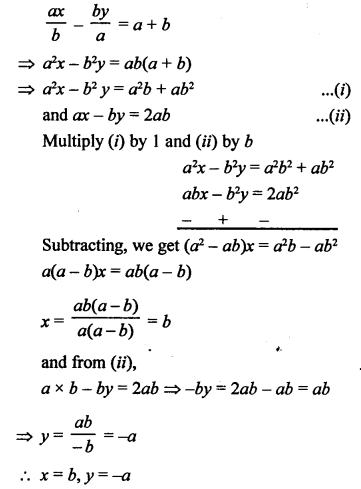
Hope given RS Aggarwal Solutions Class 10 Chapter 3 Linear equations in two variables Test Yourself are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.