RS Aggarwal Class 7 Solutions Chapter 13 Lines and Angles Ex 13

RS Aggarwal Class 7 Solutions Chapter 13 Lines and Angles Ex 13

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 13 Lines and Angles Ex 13.

Question 1.
Solution:
(i) The given angle = 35°
Let x be its complementary, then
x + 35° = 90°
⇒ x = 90° – 35° = 55°
Complement angle = 55°
(ii) The given angle = 47°
Let x be its complement, then
x + 47° = 90 ⇒ x = 90° – 47° = 43°
Complement angle = 43°
(iii) The given angles = 60°
Let x be its complement angle
x + 60° = 90° ⇒ x = 90° – 60° = 30°
Complement angle = 30°
(iv) The given angle = 73°
Let x be its complement angle
x + 73° = 90°
⇒ x = 90° – 73° = 17°
Complement angle = 17°

Question 2.
Solution:
(i) Given angle = 80°
Let x be its supplement angle, then
x + 80° = 180°
⇒ x = 180° – 80° = 100°
Supplement angle = 100°
(ii) Given angle = 54°
Let x be its supplement angle, then
x + 54° = 180°
⇒ x = 180° – 54° = 126°
Supplement angle = 126°
(iii) Given angle = 105°
let x be its supplement angle, then
x + 105° = 180°
⇒ x = 180° – 105° = 75°
Supplement angle = 75°
(iv) Given angle = 123°
Let x be its supplement angle, then
x + 123° = 180°
⇒ x = 180° – 123° = 57°
⇒ Supplement angle = 57°

Question 3.
Solution:
Let smaller angle =x
Then larger angle = x + 36°
But x + x + 36° = 180° (Angles are supplementary)
2x = 180° – 36°= 144°
x = 72°
Smaller angle = 72°
and larger angle = 72° + 36° = 108°

Question 4.
Solution:
Let angle be = x
Then other supplement angle = 180°- x
x = 180° – x
⇒ x + x = 180°
⇒ 2x = 180°
⇒ x = 90°
Hence angles are 90°, and 90°

Question 5.
Solution:
Sum of two supplementary angles is 180°
If one is acute, then second will be obtuse or both angles will be equal
Hence both angles can not be acute or obtuse
Both can be right angles only

Question 6.
Solution:
In the given figure,
AOB is a straight line and the ray OC stands on it.
∠AOC = 64° and ∠BOC = x°

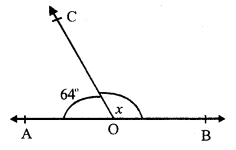
∠AOC + ∠BOC = 180° (Linear pair)
⇒ 64° + x = 180°
⇒ x = 180° – 64° = 116°
Hence x = 116°

Question 7.
Solution:
AOB is a straight line and ray OC stands on it ∠AOC = (2x – 10)°, ∠BOC = (3x + 20)°

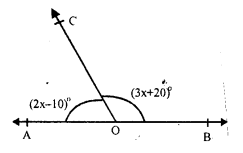
∠AOC + ∠BOC = 180° (Linear pair)
⇒ 2x – 10° + 3x + 20° = 180°
⇒ 5x + 10° = 180°
⇒ 5x = 170°
⇒ x = 34°
∠AOC = (2x – 10)° = 2 x 34° – 10 = 68° – 10° = 58°
∠BOC = (3x + 20)° = 3 x 34° + 20° – 102° + 20° = 122°

Question 8.
Solution:
AOB is a straight line and rays OC and OD stands on it ∠AOC = 65°, ∠BOD = 70° and ∠COD = x

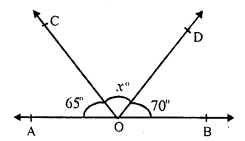
But ∠AOC + ∠COD + ∠BOD = 180° (Angles on one side of the straight line)
⇒ 65° + x + 70° = 180°
⇒ 135° + x = 180°
⇒ x = 180° – 135°
⇒ x = 45°
Hence x = 45°

Question 9.
Solution:
Two straight lines AB and CD intersect each other at O.

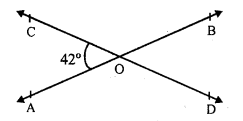
∠AOC = 42°
AB and CD intersect each other at O.
∠AOC = ∠BOD (Vertically opposite angles)
and ∠AOD = ∠BOC
But ∠AOC = 42°
∠BOD = 42°
AOB is a straight line and OC stands on it
∠AOC + ∠BOC = 180°
⇒ 42° = ∠BOC = 180°
⇒ ∠BOC = 180° – 42° = 138°
But ∠AOD = ∠BOC (vertically opposite angles)
∠AOD = 138°
Hence ∠AOD = 138°, ∠BOD = 42° and ∠COB =138°

Question 10.
Solution:
Two straight lines PQ and RS intersect at O.
∠POS = 114°
Straight lines,

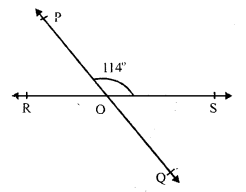
PQ and RS intersect each other at O
∠POS = ∠QOR (Vertically opposite angles)
But ∠POS = 114°
∠QOR = 114° or ∠ROQ = 114°
But ∠POS + ∠POR = 180° (Linear pair)
⇒ 114° + ∠POR = 180°
⇒ ∠POR = 180° – 114° = 66°
But ∠QOS = ∠POR (vertically opposite angles)
∠QOS = 66°
Hence ∠POR = 66°, ∠ROQ =114° and ∠QOS = 66°

Question 11.
Solution:
In the given figure, rays OA, OB, OC and OD meet at O and ZAOB – 56°,
∠BOC = 100°, ∠COD = x and ∠DOA = 74°

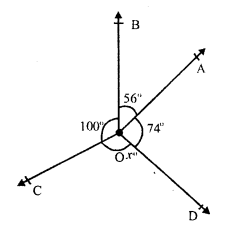
But ∠AOB + ∠BOC + ∠COD + ∠DOA = 360° (Angles at a point)
56° + 100° + x° + 74° = 360°
⇒ 230° + x° = 360°
⇒ x° = 360° – 230° = 130°
⇒ x = 130°

Hope given RS Aggarwal Solutions Class 7 Chapter 13 Lines and Angles Ex 13 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.