RS Aggarwal Class 7 Solutions Chapter 17 Constructions Ex 17B
These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 17 Constructions Ex 17B.
Other Exercises
- RS Aggarwal Solutions Class 7 Chapter 17 Constructions Ex 17A
- RS Aggarwal Solutions Class 7 Chapter 17 Constructions Ex 17B
- RS Aggarwal Solutions Class 7 Chapter 17 Constructions Ex 17C
- RS Aggarwal Solutions Class 7 Chapter 17 Constructions CCE Test Paper
Question 1.
Solution:
Steps of construction :
(i) Draw a line segment BC = 3.6cm
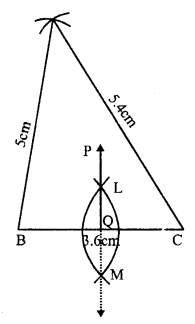
(ii) At B, draw an arc of the radius 5cm.
(iii) At C, draw another arc of the radius 5.4cm which intersects the first arc at A
(iv) Join AB and AC
(v) With centre B and C and radius more than half of BC, draw arcs intersecting each other at L and M.
(vi) Join LM which intersects BC at Q and produce it to P.
Then PQ is perpendicular bisector of side BC.
Question 2.
Solution:
Steps of construction :
(i) Draw a line segment QR = 6cm
(ii) With centre Q and radius 4.4 cm draw an arc.
(iii) With centre R and radius 5.3 cm, draw another arc intersecting the first arc at P.
(iv) Join PQ and PR.
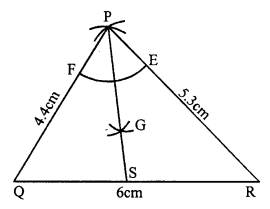
(v) With centre P and a suitable radius, draw an arc meeting PR at E and PQ at F.
(vi) With centres E and F, with same radius, draw two arcs intersecting each other at G.
(vii) Join PG and produce it to meet QR at S. Then PS is the bisector of ∠P.
Question 3.
Solution:
Steps of construction :
(i) Draw a line segment BC = 6.2 cm.
(ii) With centres B and C radius 6.2 cm, draw arcs intersecting each other at A.
(iii) Join AB and AC.
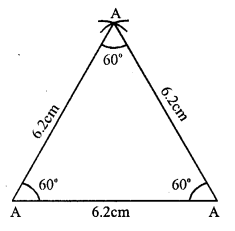
∆ABC is the required equilateral triangle.
On measuring, each angle is equal to 60°.
Question 4.
Solution:
Steps of construction :
(i) Draw a line segment BC = 5.3 cm.
(ii) With centre B and C, and radius 4.8 cm, draw arcs intersecting each other at A
(iii) Join AB and AC, Then ∆ABC is the required triangle.
(iv) Now, with centre A and a suitable radius draw an arc intersecting BC at L and M.
(v) Then with centre L and M, draw two arcs intersecting eachother at E.
(vi) Join AE intersecting BC at D. Then AD is perpendicular to BC.
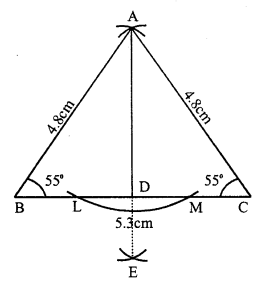
On measuring ∠B and ∠C, each is equal to 55°.
Question 5.
Solution:
Steps of construction :
(i) Draw a line segment AB = 3.8cm.
(ii) At A draw a ray AX making an angle of 60°.
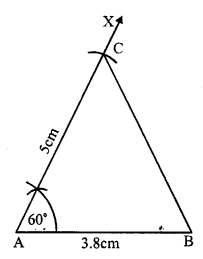
(iii) Cut off AC = 5 cm from AX
(iv) Join CB.
Then ∆ABC is the required triangle.
Question 6.
Solution:
Steps of construction :
(i) Draw a line segment BC = 4.3 cm.
(ii) At C, draw a ray CY making an angle equal to 45°.
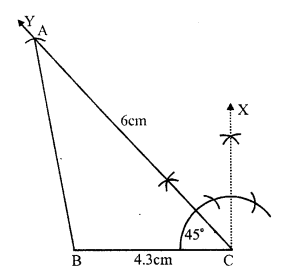
(iii) With centre C, and radius 6cm, draw an arc intersecting CY at A.
(iv) Join AB.
Then ∆ABC is the required triangle.
Question 7.
Solution:
(i) Draw a line segment AB = 5.2cm.
(ii) At A, draw a ray AX making an angle equal to 120°.
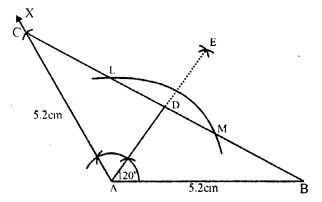
(iii) From AX cut off AC = 5.2cm.
(iv) Join BC.
Then ∆ABC is the required triangle.
(v) With centre A and some suitable radius draw an arc intersecting BC at L and M.
(vi) With centres L and M, draw two arcs intersecting each other at E.
(vii) Join AE intersecting BC at D Then AD is the perpendicular to BC.
Question 8.
Solution:
Steps of construction :
(i) Draw a line segment BC = 6.2 cm.
(ii) At B draw a ray BX making an angle of 60°.
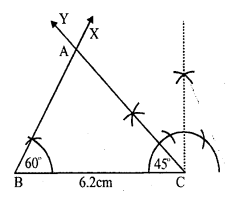
(iii) At C draw another ray CY making an angle of 45° which intersect the ray BX at A. .
Then ∆ABC is the required triangle.
Question 9.
Solution:
Steps of construction :
(i) Draw a line segment BC = 5.8 cm.
(ii) At B draw a ray BX making an angle of 30°
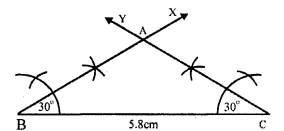
(iii) At C draw another ray CY making an angle of 30° intersecting the BX at A
Then ∆ABC is the required triangle.
On measuring AB and AC, AB = 3.5cm and AC = 3.5cm.
AB = AC
∆ABC is an isosceles triangle.
Question 10.
Solution:
Steps of construction :
In ∆ABC, ∠A = 45° and ∠C = 75°
But ∠A + ∠B + ∠C = 180°
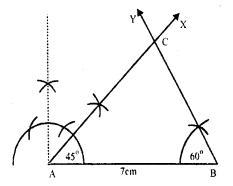
⇒ 45° + ZB + 75° = 180°
⇒ ∠B = 180° – 45° – 75°
⇒ ∠B = 180° – 120° = 60°
(i) Draw a line segment AB = 7cm.
(ii) At A, draw a ray AX making an angle of 45°.
(iii) At B, draw another ray BY making an angle of 60° which intersects AX at C
Then ∆ABC is the required triangle.
Question 11.
Solution:
Steps of construction :
(i) Draw a line segment BC = 4.8 cm
(ii) At C, draw a ray CX making an angle of 90°.
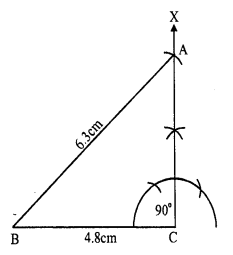
(iii) With centre B, an radius 6.3cm draw an arc intersecting CX at A.
(iv) Join AB.
Then ∆ABC is the required triangle.
Question 12.
Solution:
Steps of construction :
(i) Draw a line segment BC = 3.5cm
(ii) At B, draw a ray BX making an angle of 90°.
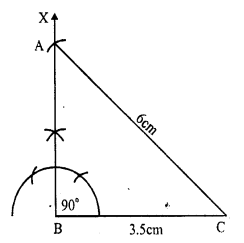
(iii) With centre C and radius 6cm draw an arc intersecting BX at A
(iv) Join AC.
Then ∆ABC is the required triangle.
Question 13.
Solution:
One acute angle = 30°, then
second acute angle will be = 90° – 30° = 60° (Sum of acute angles = 90°)
Steps of construction :
(i) Draw a line segment BC = 6cm.
(ii) At B draw a ray BX making an angle of 30°.
(iii) At C draw another ray CY making an angle of 60° which intersects BX at A
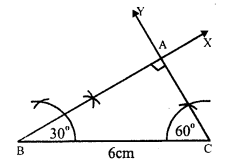
Then ∆ABC is the required triangle.
Hope given RS Aggarwal Solutions Class 7 Chapter 17 Constructions Ex 17B are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.