RS Aggarwal Class 7 Solutions Chapter 20 Mensuration Ex 20D

RS Aggarwal Class 7 Solutions Chapter 20 Mensuration Ex 20D

These Solutions are part of RS Aggarwal Solutions Class 7. Here we have given RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20D.

Other Exercises

• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20A
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20B
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20C
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20D
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20E
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20F
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20G
• RS Aggarwal Solutions Class 7 Chapter 20 Mensuration CCE Test Paper

Question 1.
Solution:
(i) Base of the triangle = 42 cm

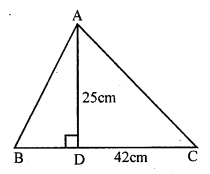
Height = 25 cm
Area = \(\frac { 1 }{ 2 }\) x base x height
= \(\frac { 1 }{ 2 }\) x 42 x 25 = 525 cm²
(ii) Base of the triangle = 16.8 m
and height = 75 cm = 0.75 m
Area = \(\frac { 1 }{ 2 }\) x Base x height
= \(\frac { 1 }{ 2 }\) x 16.8 x 0.75 m2 = 6.3 m²
(iii) Base of a triangle (b) = 8 m = 80 cm
and height (h) = 35 cm
Area = \(\frac { 1 }{ 2 }\) bh = \(\frac { 1 }{ 2 }\) x 80 x 35 = 1400 cm²

Question 2.
Solution:
Base of triangle = 16 cm
area of the triangle = 72 cm²

Question 3.
Solution:
Area of triangular region = 224 m²
Base = 28 m

Question 4.
Solution:
Area of triangle = 90 cm²
and height (h) = 12 cm

Question 5.
Solution:
Let height of a triangular field = x m
Then base (b) = 3x m
and area = \(\frac { 1 }{ 2 }\) bh = \(\frac { 1 }{ 2 }\) x 3x x x

Question 6.
Solution:
Area of the right angled triangle = 129.5 cm²

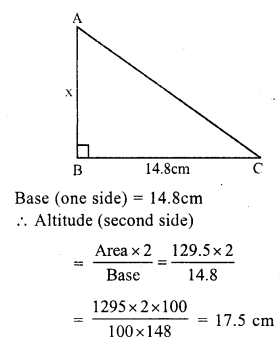
Question 7.
Solution:
In right angled ∆ABC,
Base BC = 1.2 m

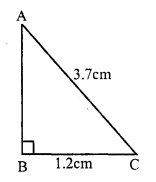
and hypotenuse AC = 3.7 m
But AC² = AB² + BC² (Pythagoras Theorem)
⇒ (3.7)² = AB² + (1.2)²
⇒ 13.69 = AB² + 1.44
⇒ AB² = 13.69 – 1.44
⇒ AB² = 12.25 = (3.5)²
⇒ AB = 3.5 m
Now, area of ∆ABC = \(\frac { 1 }{ 2 }\) x base x altitude
= \(\frac { 1 }{ 2 }\) x 1.2 x 3.5 m² = 2.1 m²

Question 8.
Solution:
Legs of a right angled triangle = 3 : 4
Let one leg (base) = 3x

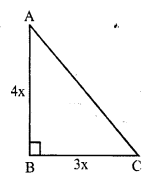
Then second leg (altitude) = 4x
Area = \(\frac { 1 }{ 2 }\) x base x altitude
= \(\frac { 1 }{ 2 }\) x 3x x 4x = 6x²
6x² = 1014
⇒ x² = \(\frac { 1014 }{ 6 }\) = 169 = (13)²
x = 13
one leg'(Base) = 3x = 3 x 13 = 39 cm
and second leg (altitude) = 4x = 4 x 13 = 52 cm

Question 9.
Solution:
One side BC of a right triangular scarf = 80 cm

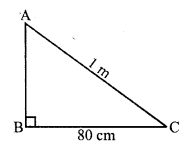
and longest side AC = 1 m = 100 cm
By Pythagoras Theorem,
AC² = AB² + BC²
⇒ (100)² = AB² + (80)²
⇒ 10000 = AB² + 6400
⇒ AB² = 10000 – 6400
⇒ AB² = 3600 = (60)²
⇒ AB = 60
Second side = 60 cm
Area of the scarf = \(\frac { 1 }{ 2 }\) x b x h
= \(\frac { 1 }{ 2 }\) x 80 x 60 cm2 = 2400 cm²
Rate of cost = Rs. 250 per m²
Total cost =\(\frac { 2400 }{ 100 x 100 }\) x 250 = Rs. 60

Question 10.
Solution:
(i) Side of the equilateral triangle (a) = 18 cm

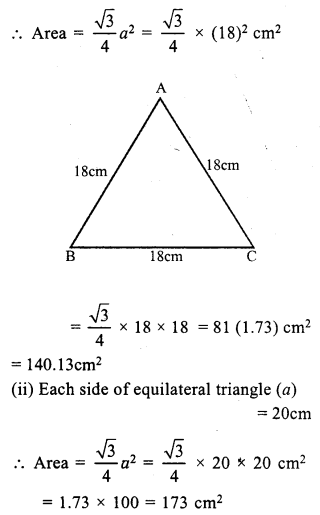
Question 11.
Solution:
Area of equilateral triangle = 16√3 cm²
Let each side = a
then \(\frac { \surd 3 }{ 4 }\) a² = 16√3
⇒ a² = \(\frac { 16\surd 3\times 4 }{ \surd 3 }\)
⇒ a² = 64 = (8)²
a = 8 cm
Each side = 8 cm

Question 12.
Solution:
Each side of an equilateral triangle = 24cm
Length of altitude = \(\frac { \surd 3 }{ 2 }\) a = \(\frac { \surd 3 }{ 2 }\) x 24
= 12√3 cm = 12 (1.73) = 20.76 cm

Question 13.
Solution:
(i) a = 13 m, b = 14 m, c = 15 m

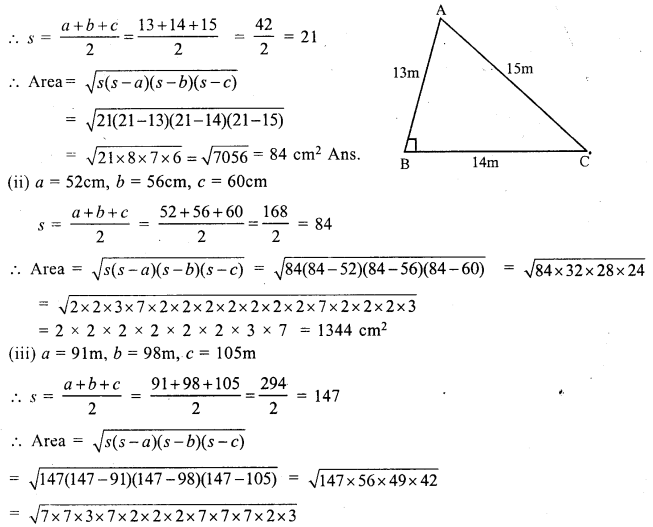
= 2 x 2 x 3 x 7 x 7 x 7 = 4116 m²

Question 14.
Solution:
Let a = 33 cm, b = 44 cm, c = 55 cm

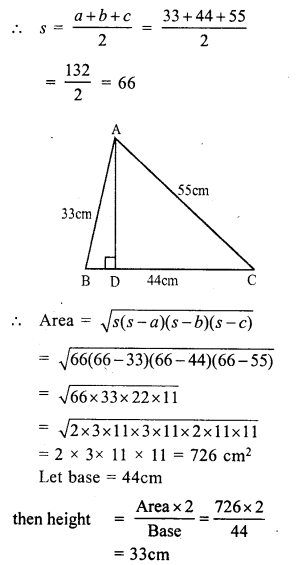
Question 15.
Solution:
Perimeter of the triangle = 84 cm
Ratio in side = 13 : 14 : 15
Sum of ratios =13 + 14 + 15 = 42
Let then first side = \(\frac { 84 x 13 }{ 42 }\) = 26 cm

Question 16.
Solution:
Let a = 42 cm, b = 34 cm, c = 20 cm

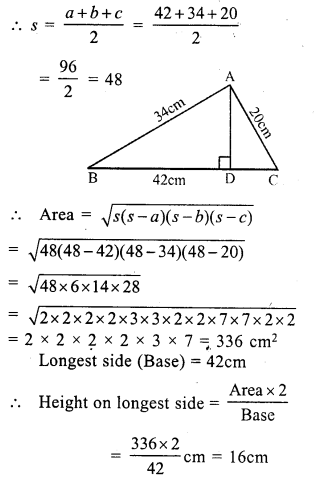
Question 17.
Solution:
In isosceles ∆ABC
Base BC = 48 cm.
and AB = AC = 30cm.
Let AD ⊥ BC

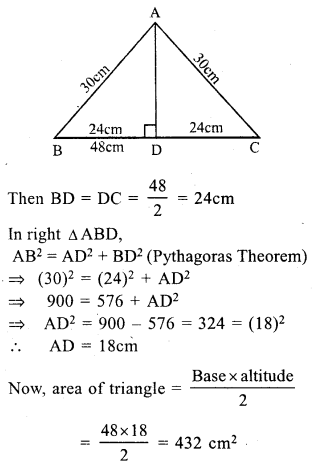
Question 18.
Solution:
Perimeter of an isosceles triangle = 32 cm
Base = 12 cm
Sum of two equal sides = 32 – 12 = 20 cm
Length of each equal side = \(\frac { 20 }{ 2 }\) = 10cm
Let AD ⊥ BC
BD = DC = \(\frac { 12 }{ 2 }\) = 6 cm

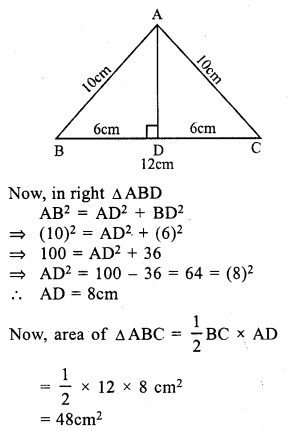
Question 19.
Solution:
In quadrilateral ABCD,
diagonal AC = 26 cm.

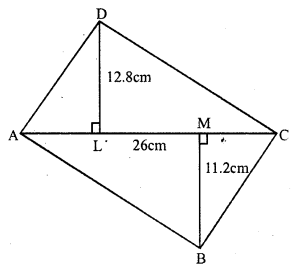
and perpendiculars DL = 12.8cm, BM = 11.2 cm
Area of quadrilateral ABCD
= \(\frac { 1 }{ 2 }\) (Sum of perpendicular) x diagonal
= \(\frac { 1 }{ 2 }\) (12.8 + 11.2) x 26 cm²
= \(\frac { 1 }{ 2 }\) x 24 x 26 = 312 cm²

Question 20.
Solution:
In quad. ABCD,
AB = 28 cm, BC = 26 cm, CD = 50 cm, DA = 40 cm
and diagonal AC = 30 cm
In ∆ABC,

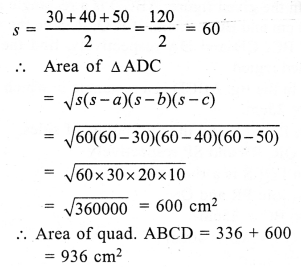
Question 21.
Solution:
ABCD is a rectangle in which AB = 36 m
and BC = 24m
In ∆AED,
EF = 15 m
AD = BC = 24 m.
Now area of rectangle ABCD = l x b = 36 x 24 cm² = 864 cm²
Area of ∆AED = \(\frac { 1 }{ 2 }\) x AD x EF
= \(\frac { 1 }{ 2 }\) x 24 x 15 cm² = 180 cm²
Area of shaded portion = 864 – 180 = 684 m²

Question 22.
Solution:
In the fig. ABCD is a rectangle in which AB = 40 cm, BC = 25 cm.
P, Q, R and S and the mid points of sides, PQ, QR, RS and SP respectively
Then PQRS is a rhombus.
Now, join PR and QS.
PR = BC = 25cm and QS = AB = 40cm
Area of PQRS = \(\frac { 1 }{ 2 }\) x PR x QS
= \(\frac { 1 }{ 2 }\) x 25 x 40 = 500 cm²

Question 23.
Solution:
(i) Length of rectangle (l) = 18 cm
and breadth (b) = 10 cm
Area = l x b = 18 x 10 = 180 cm²

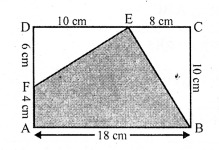
Area of right ∆EBC = \(\frac { 1 }{ 2 }\) x 10 x 8 = 40 cm²
and area of right ∆EDF = \(\frac { 1 }{ 2 }\) x 10 x 6 = 30 cm²
Area of shaded region = 180 – (40 + 30) = 180 – 70 = 110 cm²
(ii) Side of square = 20 cm

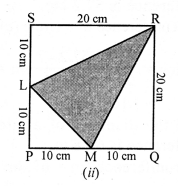
Area of square = a² = (20)² = 400 cm²
Area of right ∆LPM = \(\frac { 1 }{ 2 }\) x 10 x 10 cm² = 50 cm²
Area of right ∆RMQ = \(\frac { 1 }{ 2 }\) x 10 x 20 = 100 cm²
and area of right ∆RSL = \(\frac { 1 }{ 2 }\) x 20 x 10 = 100 cm²
Area of shaded region = 400 – (50 + 100 + 100) cm2 = 400 – 250 = 150 cm²

Question 24.
Solution:
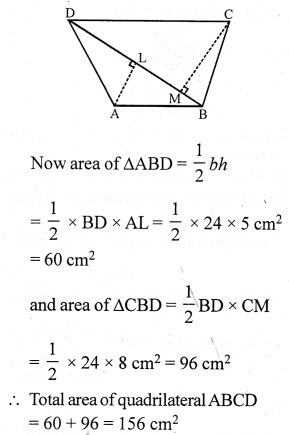
In the quadrilateral ABCD
BD = 24 cm
AL ⊥ BD and CM ⊥ BD
AL = 5 cm and CM = 8 cm

Hope given RS Aggarwal Solutions Class 7 Chapter 20 Mensuration Ex 20D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.