RS Aggarwal Class 8 Solutions Chapter 14 Polygons Ex 14B

RS Aggarwal Class 8 Solutions Chapter 14 Polygons Ex 14B

These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 14 Polygons Ex 14B.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 14 Polygons Ex 14A
• RS Aggarwal Solutions Class 8 Chapter 14 Polygons Ex 14B

Question 1.
Solution:
In a pentagon, no. of diagonals
\(=\frac { n\left( n-3 \right) }{ 2 }\)
\(=\frac { 5\left( 5-3 \right) }{ 2 }\)
\( =\frac { 5\times 2 }{ 2 } \)
= 5 (a)

Question 2.
Solution:
In a hexagon, no. of diagonals
\(=\frac { n\left( n-3 \right) }{ 2 }\)
\(=\frac { 6\left( 6-3 \right) }{ 2 }\)
\( =\frac { 6\times 3 }{ 2 } \)
= 9 (c)

Question 3.
Solution:
In an octagon, no. of diagonals
\(=\frac { n\left( n-3 \right) }{ 2 }\)
\(=\frac { 8\left( 8-3 \right) }{ 2 }\)
\( =\frac { 8\times 5 }{ 2 } \)
= 20 (d)

Question 4.
Solution:
In a polygon of 12 sides, no. of diagonals
\(=\frac { n\left( n-3 \right) }{ 2 }\)
\(=\frac { 12\left( 12-3 \right) }{ 2 }\)
\( =\frac { 12\times 9 }{ 2 } \)
= 54 (c)

Question 5.
Solution:
A polygon has 27 diagonal

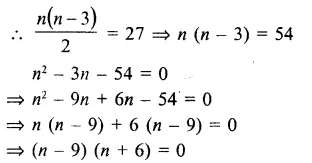
Either n – 9 = 0, then n = 9
or n + 6 = 0, then n = – 6 but it is not possible being negative
No. of sides = 9 (c)

Question 6.
Solution:
Angles of a pentagon are x°, (x + 20)°, (x + 40)°, (x + 60°) and (x + 80)°
But sum of angle of a pentagon

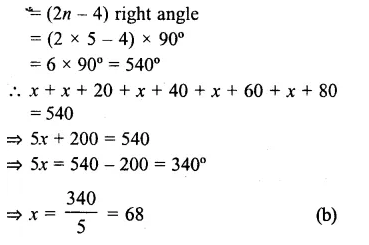
Question 7.
Solution:
Measure of each exterior angle = 40°
No. of sides = \(\frac { { 360 }^{ o } }{ 40 }\)9 sides (b)

Question 8.
Solution:
Each interior angle of a polygon = 108°

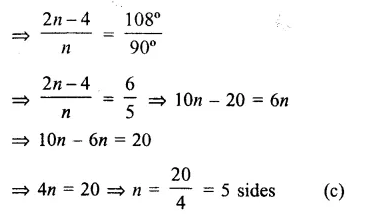
Question 9.
Solution:
Each interior angle = 135°

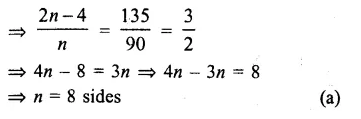
Question 10.
Solution:
Let each exterior angle = x, then
Each interior angles = 3n
But sum of angle = 180°
x + 3x = 180°
=>4x = 180°
=> x = 45°
No. of sides = \(\frac { { 360 }^{ o } }{ 45 } \)
= 8 sides (b)

Question 11.
Solution:
Each interior angles of decagon

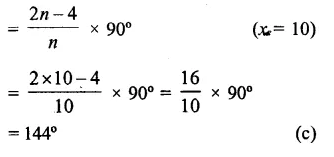
Question 12.
Solution:
Sum of all interior angles of a hexagon
= (2n – 4) x right angle
= (2 x 6 – 4) right angle
= 8 right angles (b)

Question 13.
Solution:
Sum of all interior angles of polygon = 1080°
Let n be the number of sides, then
(2n – 4) x 90°= 1080°

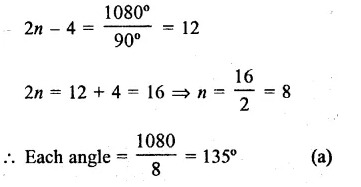
Question 14.
Solution:
Difference between each interior and exterior angle = 108°
Then each interior angle = x + 108°
x + x + 108°= 180°
(Sum of both angles = 180°)
=> 2x = 180° – 108° = 72°
x = \(\\ \frac { 72 }{ 2 } \)
= 36°
No. of sides = \( \frac { { 360 }^{ o } }{ { 36 }^{ o } } \)
= 10 (d)

Hope given RS Aggarwal Solutions Class 8 Chapter 14 Polygons Ex 14B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.