RS Aggarwal Class 8 Solutions Chapter 16 Parallelograms Ex 16A

RS Aggarwal Class 8 Solutions Chapter 16 Parallelograms Ex 16A

These Solutions are part of RS Aggarwal Solutions Class 8. RS Aggarwal Solutions Class 8 Chapter 16 Parallelograms Ex 16A.

Other Exercises

• RS Aggarwal Solutions Class 8 Chapter 16 Parallelograms Ex 16A
• RS Aggarwal Solutions Class 8 Chapter 16 Parallelograms Ex 16B

Question 1.
Solution:
In ||gm ABCD,
∠A = 110°
But ∠ C = ∠ A {Opposite angles of a ||gm are equal}

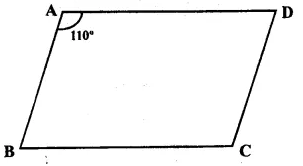
∴ ∠C = 110°
But ∠A + ∠B = 180°
(Sum of adjacent angles)
=> 110° + ∠B = 180°
=> ∠B – 180° – 110° = 70°
But ∠ D = ∠ B (opposite angles)
∴ ∠ D = 70°
Hence ∠B = 70°, ∠C = 110° and ∠D = 70° Ans.

Question 2.
Solution:
In a parallelogram, sum of two adjacent angles is 180°
But these are equal to each other
∴ Each angle will be \(\frac { 180^{ o } }{ 2 } \)
= 90° Ans.

Question 3.
Solution:
The ratio between two adjacent angles of a ||gm ABCD are in the ratio 4 : 5

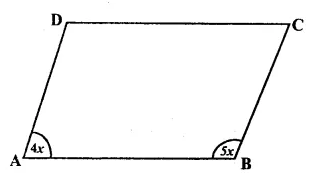
Let ∠ A = 4x and ∠ B = 5x
But ∠A + ∠B = 180°
=> 4x + 5x = 180°
=> 9x = 180°
∴ x = \(\frac { 180^{ o } }{ 9 } \)
= 20°
∴ ∠A = Ax = 4 x 20° = 80°
∠B = 5x = 5 x 20 = 100° Ans.

Question 4.
Solution:
In || gm ABCD, ∠ A and ∠ B are two adjacent angles
Let ∠ A = (3x – 4)° and ∠ B = (3x + 16)°
But ∠A + ∠B = 180°

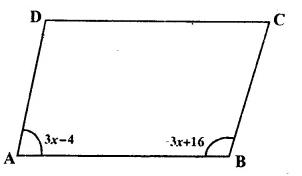
=> (3x – 4)° + (3x + 16) = 180°
=> 3x – 4° + 3x + 16° = 180°
=> 6x + 12° = 180°
=> 6x= 180° – 12°
=> 6x = 168
=> x = \(\\ \frac { 168 }{ 6 } \) = 28°
∴ x = 28°
Now ∠A = 3x – 4 = 3 x 28° – 4° = 84° – 4° = 80°
∠B = 3x + 16
= 3 x 28 + 16
= 84°+ 16° = 100°
But ∠C = ∠A (opposite angles of ||gm)
∴ ∠ C = 80°
Similarly ∠ D = ∠ B = 100°
Hence ∠A = 80°, ∠B = 100°, ∠C = 80° and ∠D= 100° Ans.

Question 5.
Solution:
In ||gm ABCD, ∠A and ∠C are opposite angles.
∴ ∠A = ∠C= 130°

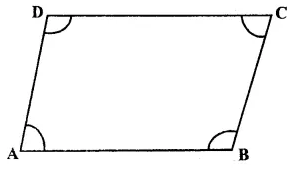
But ∠A = ∠C (opposite angles)
∴ ∠A = ∠C
= \(\frac { 130^{ o } }{ 2 } \)
= 65°
But ∠A + ∠B = 180°
(sum of adjacent angles)
=> 65° + ∠B = 180°
=> ∠B = 180° – 65° = 115°
But ∠ D = ∠ B (opposite angles)
∴ ∠D = 115°
Hence ∠A = 65°, ∠B = 115°, ∠C = 65° and ∠ D = 115° Ans.

Question 6.
Solution:
Let ABCD is a parallelogram in which AB : BC = 5:3
Let AB = 5x: and BC = 3x.

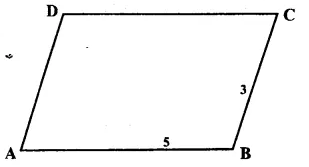
But perimeter = 64 cm.
∴ 2(5x + 3x) = 64
=> 2 x 8x = 64
=> 16x = 64
x = \(\\ \frac { 64 }{ 16 } \)
= 4
∴ AB = 5x = 5 x 4 = 20 cm
BC = 3x = 3 x 4=12 cm
But CD = AB and AD = BC
(opposite sides of ||gm)
∴ CD = 20 cm and AD = 12 cm Ans.

Question 7.
Solution:
Perimeter of parallelogram ABCD = 140 cm.
=> ∴ 2 (AB + BC) = 140 cm.
=> AB + BC = \(\\ \frac { 140 }{ 2 } \) = 70 cm.
Let BC = x

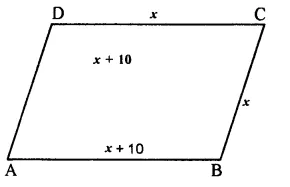
then AB = x + 10
∴ x + x + 10 = 70
=> 2x + 10 = 70
=> 2x = 70 – 10 = 60
=>x = \(\\ \frac { 60 }{ 2 } \) = 30
∴ BC = 30 cm. and
AB = 30 + 10 = 40 cm.
But AD = BC and CD = AB
(Opposite sides of parallelogram)
∴ AD = 30 cm. and CD = 40 cm.

Question 8.
Solution:
In rectangle ABCD, AC is diagonal BM ⊥ AC and DN ⊥ AC.
Now, we have to prove that
∆BMC ≅ ∆DNA
In ∆BMC and ∆DNA,
BC = AD (opposite sides of the rectangle)
∠M = ∠N (each = 90°)
∠BCM = ∠D AN (Alternate angles)
∴ ∆BMC ≅ ∆DNA
(S.A.A. axiom of congruency)
∴ BM = DN (c.p .c.t.)

Question 9.
Solution:
ABCD is a parallelogram.
AE and CF are the bisectors of ∠A and ∠C respectively.
In ∆ADE and ∆CBF,
AD = BC
(Opposite sides of the parallelogram)
∠D = ∠B
(Opposite angles of the parallelogram)
∠DAE = ∠FCB (\(\\ \frac { 1 }{ 2 } \) of equal angles)
∴ ∆ADE ≅ ∆CBF
(S.A.A. axiom of congruency)
∴ DE = BF (c.p.c.t.)
But CD = AB
(Opposite sides of the parallelogram)
∴ CD – DE = AB – BF
=> EC = AF
and AB || CD
∴ AFCE is a parallelogram
∴ AE || CF.

Question 10.
Solution:
Let ABCD is a rhombus AC and BD are its diagonals which bisect each other at right angles at O.
AC = 16cm and BD = 12cm
∴ AO = \(\\ \frac { 16 }{ 2 } \) = 8cm

BO = \(\\ \frac { 12 }{ 2 } \) = 6 cm
Now, in right ∆AOB
AB² = AO² + BO²
(Pythagorus Theorem)
= (8)² + (6)²
= 64 + 36 = 100 = (10)²
∴ AB = 10 cm
But all the sides of a rhombus are equal
∴ Each side will be 10 cm Ans.

Question 11.
Solution:
In square ABCD, AC is its diagonal
∴ Diagonals of a square bisect each angle at the vertex
∴ ∠ CAD = ∠ CAB
But ∠ DAB = 90° (Angle of a square)
∴ ∠ CAD = ∠ CAB = \(\\ \frac { 1 }{ 2 } \) ∠ DAB
= \(\\ \frac { 1 }{ 2 } \) x 90° = 45°
Hence ∠ CAD = 45° Ans.

Question 12.
Solution:
Let ABCD is a rectangle
AB : BC = 5 : 4
Let AB = 5x and BC = 4x.
But perimeter = 90cm

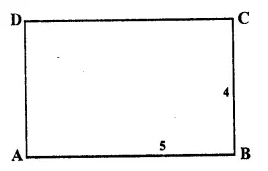
2(AB + BC) = 90
=> 2(5x + 4x) = 90
=> 2 x 9x = 90
=> 18x = 90
x = \(\\ \frac { 90 }{ 18 } \) = 5
∴ Length (AB) = 5x = 5 x 5 = 25 cm
Breadth (BC) = 4x = 4 x 5 = 20 cm Ans.

Question 13.
Solution:
(i) It is a rectangle
(ii) Square
(iii) rhombus
(iv) rhombus
(v) square
(vi) rectangle.

Question 14.
Solution:
(i) False
(ii) False
(iii) False
(iv) False
(v) False
(vi) True
(vii) True
(viii) True
(ix) False
(x) True

 

Hope given RS Aggarwal Solutions Class 8 Chapter 16 Parallelograms Ex 16A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.