RS Aggarwal Class 8 Solutions Chapter 17 Construction of Quadrilaterals Ex 17B
These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 17 Construction of Quadrilaterals Ex 17B.
Other Exercises
- RS Aggarwal Solutions Class 8 Chapter 17 Construction of Quadrilaterals Ex 17A
- RS Aggarwal Solutions Class 8 Chapter 17 Construction of Quadrilaterals Ex 17B
Question 1.
Solution:
Steps of Construction :
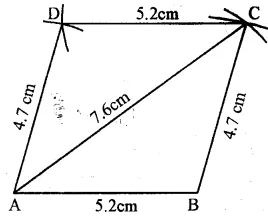
(i) Draw a line segment AB = 5.2 cm.
(ii) With centre A and radius 7.6 cm. and with centre B and radius 4.7 cm. draw arcs which intersect each other at C.
(iii) Join AC and BC.
(iv) Again with centre A and radius 4.7 cm and with centre C and radius 5.2 cm draw arcs which intersect each other at D.
(v) Join AD and CD.
ABCD is the required parallelogram.
Question 2.
Solution:
Steps of Construction :
(i) Draw a line segment AB = 4.3 cm.
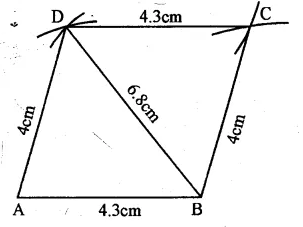
(ii) With centre A and radius 4 cm. and with centre B and radius 6.8 cm., draw arcs which intersect each other at D.
(iii) Join AD and BD.
(iv) Again with centre B and radius 4 cm. and with centre D and radius 4.3 cm., draw arcs intersecting each other at C.
(v) Join DC and BC. ABCD is the required parallelogram.
Question 3.
Solution:
Steps of Construction :
(i) Draw a line segment PQ = 4 cm.
(ii) At Q, draw a ray making an angle of 60° and cut off QR = 6 cm.
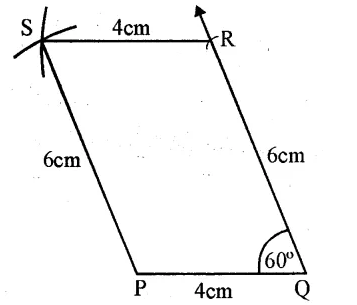
(iii) With centre P and radius 6 cm. and with centre R and radius 4 cm draw arcs intersecting each other at S.
(iv) Join RS and PS.
PQRS is the required parallelogram. Q.
Question 4.
Solution:
Steps of Construction :
(i) Draw a line segment BC = 5 cm.
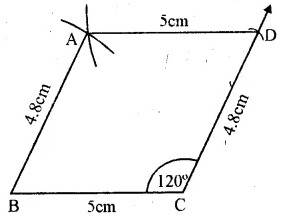
(ii) At C, draw a ray making an angle of 120° and cut off CD = 4.8 cm.
(iii) With centre B and radius 4.8 cm. with centre D and radius 5 cm, draw arcs intersecting each other at A.
(iv) Join AB and AD
ABCD is the required parallelogram.
Question 5.
Solution:
Steps of Construction :
We know that diagonals of a parallelogram bisect each other.
(i) Draw a line segment AB = 4.4 cm.
(ii) With centre A and radius \(\\ \frac { 5.6 }{ 2 } \) cm and with centre B and radius \(\\ \frac { 7 }{ 2 } \) = 3.5 cm. draw arcs
intersecting each other at O.
(iii) Join AO and BO and produce them to C and D respectively such that OC = 2.8 cm and OD = 3.5 cm.
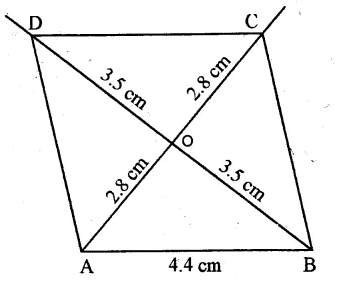
(iv) Join AD, CD and BC
ABCD is the required parallelogram
Question 6.
Solution:
Steps of Construction :
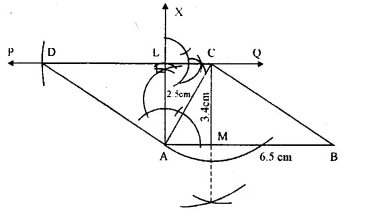
(i) Draw a line segment AB = 6.5 cm.
(ii) At A, draw a perpendicular AX and cut off AL = 2.5 cm.
(iii) Through L, draw a line PQ parallel to AB.
(iv) From A, draw an arc of radius 3 -4 cm which intersects the line PQ at C.
(v) Join AC. BC
(vi) From PQ, cut off CD = AB.
(vii) Join AD
(viii) From C, draw a perpendicular CM to AB.
ABCD is the required parallelogram.
Question 7.
Solution:
Steps of Construction :
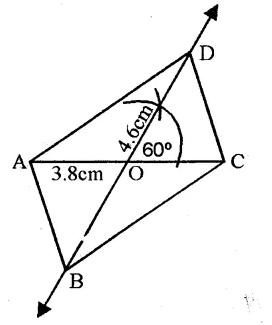
(i) Draw a line segment AC = 3.8 cm.
(ii) Bisect it at O.
(iii) At O, draw a ray making an angle of 60° and produce it both sides.
(iv) From O cut off OB = OD = 2.3 cm.
(v) Join AB, BC, CD and AD.
ABCD is the required parallelogram.
Question 8.
Solution:
Steps of Construction :
(i) Draw a line segment AB = 11 cm.
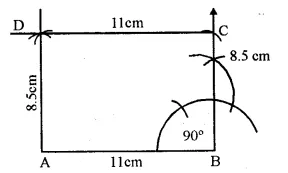
(ii) At B, draw a perpendicular and cut off BC = 8.5 cm.
(iii) With centre A and radius 8.5 cm and with centre C and radius 11 cm, draw arcs intersecting each other at D.
(iv) Join AD and CD.
ABCD is the required rectangle.
Question 9.
Solution:
Steps of Construction :
(i) Draw a line segment AB = 6.4 cm.
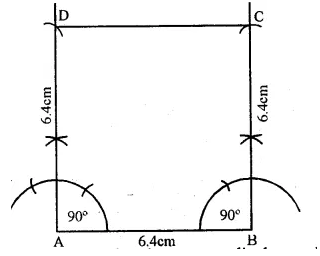
(ii) At A and B draw perpendiculars and
cut off AD = BC = AB = 6.4 Cm.
(iii) Join CD.
ABCD is the required square.
Question 10.
Solution:
Steps of Construction :
(i) Draw a line segment AC = 5.8 cm.
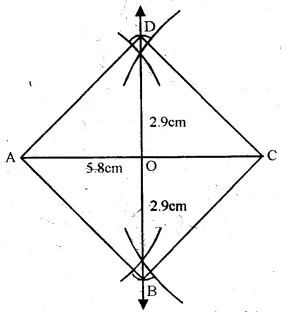
(ii) Draw its perpendicular bisector intersecting AC at O.
(iii) From O, cut off OD = OB = 2.9 cm.
\(\qquad =\left( \frac { 1 }{ 2 } BD \right) \)
(iv) Join AB, BC, CD and DA. ABCD is the required square.
Question 11.
Solution:
Steps of Construction :
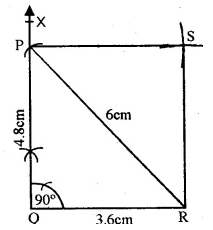
(i) Draw a line segment QR = 3.6 cm.
(ii) At Q, draw a ray QX making an angle of 90°.
(iii) With centre R and radius 6 cm. draw an arc which intersects QX at P.
(iv) Join PR.
(v) With centre P and radius equal to QR and with centre R and radius equal to QP, draw arcs intersecting each other at S.
(vi) Join PS and RS.
PQRS is the required rectangle.
The length of other side PQ = 4.8 cm.
Question 12.
Solution:
Steps of Construction :
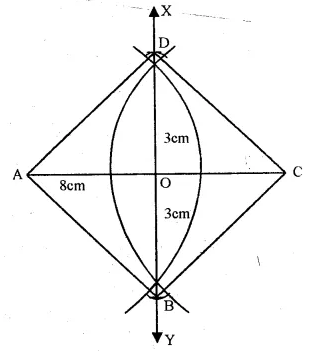
(i)Draw a line segment AC = 8 cm.
(ii)Draw its perpendicular bisector intersecting it at O.
(iii)From O, cut off OB = OD = 3 cm.
(iv)Join AB, BC, CD and DA.
ABCD is the required rhombus.
Question 13.
Solution:
Steps of Construction :
(i)Draw a line segment AC = 6.5 cm.
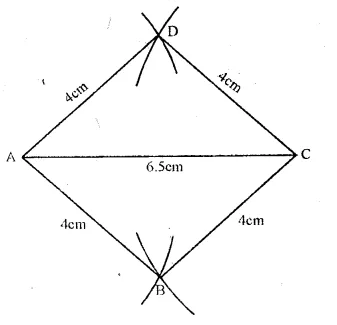
(ii) With centres A and C and radius equal to 4 cm., draw arcs which intersect each other on both sides of line segment AC at B and D respectively.
(iii) Join AB, BC, CD and DA.
ABCD is the required rhombus.
Question 14.
Solution:
Steps of Construction :
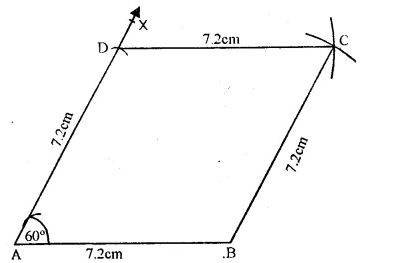
(i)Draw a line segmentAB = 7.2 cm.
(ii)At A draw a ray AX making an angle of 60° and cut off AD = 7.2 cm.
(iii)With centres D and B, and radius 7.2 cm., draw arcs intersecting each other at C.
(iv)Join CD and CB.
ABCD is the required rhombus.
Question 15.
Solution:
Steps of Construction :
(i) Draw a line segment AB = 6 cm
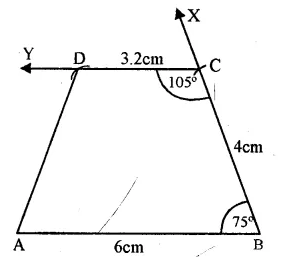
(ii)At B, draw a ray BX making an angle of 75° and cut off BC = 4 cm.
(iii) At C, draw a ray CY making an angle of 180° – 75° = 105°
So that CY may be parallel to AB.
(iv) From CY, Cut off CD = 3.2 cm.
(v) Join DA.
ABCD is the required trapezium.
Question 16.
Solution:
Steps of Construction :
(i) Draw a line segment AB = 7 cm.
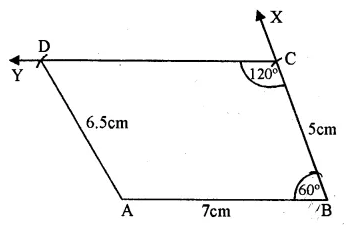
(ii) At B, draw a ray BX making an angle of 60° and cut off BC = 5 cm.
(iii) At C, draw a ray CY making an angle of (180° – 60°) = 120° so that CY || AB.
(iv) With centre A and radius 6.5 cm. draw an arc intersecting CY at D.
(v) Join AD,
ABCD is the required trapezium.
Hope given RS Aggarwal Solutions Class 8 Chapter 17 Construction of Quadrilaterals Ex 17B are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.