RS Aggarwal Class 8 Solutions Chapter 8 Linear Equations Ex 8A
These Solutions are part of RS Aggarwal Solutions Class 8. Here we have given RS Aggarwal Solutions Class 8 Chapter 8 Linear Equations Ex 8A.
Other Exercises
- RS Aggarwal Solutions Class 8 Chapter 8 Linear Equations Ex 8A
- RS Aggarwal Solutions Class 8 Chapter 8 Linear Equations Ex 8B
- RS Aggarwal Solutions Class 8 Chapter 8 Linear Equations Ex 8C
Solve :
Question 1.
Solution:
8x + 3 = 27 + 2x
=> 8x – 2x
=> 27 – 3
=> 6x = 24
=> x = \(\\ \frac { 24 }{ 6 } \) = 4
x = 4
Question 2.
Solution:
5x + 7 = 2x – 8
=> 5x – 2x = – 8 – 7
=> 3x = – 15
=> x = \(\\ \frac { -15 }{ 3 } \) = – 5
x = – 5
Question 3.
Solution:
2z – 1 = 14 – z
=> 2z + z = 14 + 1
=> 3z = 15
=> z = \(\\ \frac { 15 }{ 3 } \) = 5
z = 5
You can also Download NCERT Solutions for Class 8 Maths to help you to revise complete Syllabus and score more marks in your examinations.
Question 4.
Solution:
9x + 5 = 4(x – 2) +8
=> 9x + 5 = 4x – 8 + 8
=> 9x – 4x = – 8 + 8 – 5
=> 5x = – 5
=> x = \(\\ \frac { -5 }{ 5 } \) = – 1
x = – 1
Question 5.
Solution:
\(\\ \frac { 7y }{ 5 } \) = y – 4
Multiplying both sides by 5,
\(\\ \frac { 7y }{ 5 } \) x 5 = 5(y – 4)
=> 5 (y-4)
=> 7y = 5y – 20
=> 7y – 5y = – 20
=> 2y = – 20
=> y = \(\\ \frac { -20 }{ 2 } \) = – 10
Hence y = – 10 Ans.
Question 6.
Solution:
3x + \(\\ \frac { 2 }{ 3 } \) = 2x + 1
=> 3x – 2x = 1 – \(\\ \frac { 2 }{ 3 } \)
=> x = \(\\ \frac { 3-2 }{ 3 } \) = \(\\ \frac { 1 }{ 3 } \)
Hence x = \(\\ \frac { 1 }{ 3 } \) Ans.
Question 7.
Solution:
15(y – 4) – 2(y – 9) + 5(y + 6) = 0
15y – 60 – 2y + 18 + 5y + 30 = 0
=> 15y – 2y + 5y = 60 – 18 – 30
=> 18y = 12
=> y = \(\\ \frac { 12 }{ 18 } \) = \(\\ \frac { 2 }{ 3 } \)
=> y = \(\\ \frac { 2 }{ 3 } \)
Question 8.
Solution:
3(5x – 7) – 2(9x – 11) = 4(8x – 13) – 17
=> 15x – 21 – 18x + 22 = 32x – 52 – 17
=> 15x – 18x – 32x = – 52 – 17 + 21 – 22
=> 15x – 50x = – 70
=> – 35x = – 70
=> x = \(\\ \frac { -70 }{ -35 } \) = 2
x = 2
Question 9.
Solution:
\(\\ \frac { x-5 }{ 2 } \) – \(\\ \frac { x-3 }{ 5 } \) = \(\\ \frac { 1 }{ 2 } \)
Multiplying each term by 10, the L.C.M. of 2 and 5
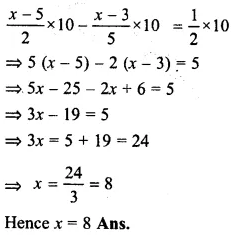
Question 10.
Solution:
\(\\ \frac { 3t-2 }{ 4 } \) – \(\\ \frac { 2t+3 }{ 3 } \) = \(\\ \frac { 2 }{ 3 } \) – t
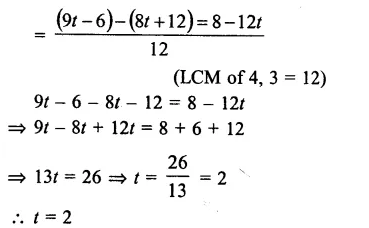
Question 11.
Solution:
\(\frac { 2x+7 }{ 5 } +\frac { 3x+11 }{ 2 } =\frac { 2x+8 }{ 3 } -5\)
Multiplying by 30, the L.C.M. of 5, 2 and 3.
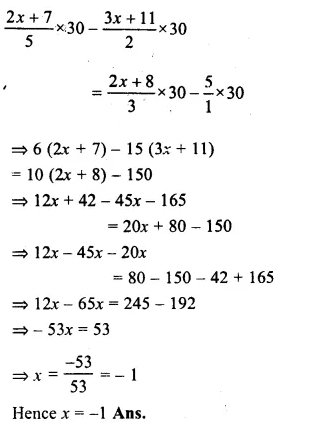
Question 12.
Solution:
\(\frac { 5x-4 }{ 6 } =4x+1-\frac { 3x+10 }{ 2 } \)
Multiplying by 6, the L.C.M. of 6 and 2
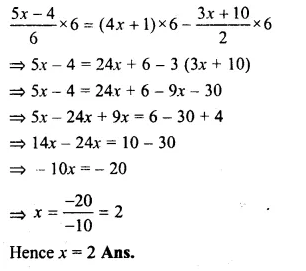
Question 13.
Solution:
\(5x-\frac { 1 }{ 3 } \left( x+1 \right) =6\left( x+\frac { 1 }{ 30 } \right) \)
=> 5x – \(\\ \frac { x+1 }{ 3 } \) = 6x + \(\\ \frac { 1 }{ 5 } \)
Multiplying by 15, the L.C.M. of 3 and 5
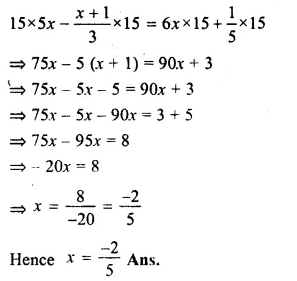
Question 14.
Solution:
\(4-\frac { 2\left( z-4 \right) }{ 3 } =\frac { 1 }{ 2 } \left( 2z+5 \right)\)
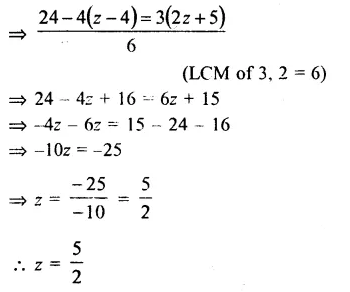
Question 15.
Solution:
\(\frac { 3\left( y-5 \right) }{ 4 } -4y=3-\frac { \left( y-3 \right) }{ 2 } \)
Multiplying by 4, the L.C.M. of 4 and 2
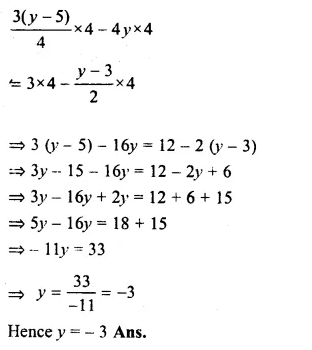
Question 16.
Solution:
\(\\ \frac { 8x-3 }{ 3x } \) = \(\\ \frac { 2 }{ 1 } \)
By cross multiplication,
8x – 3 = 6x
=> 8x – 6x = 3
=> 2x = 3
=> x = \(\\ \frac { 3 }{ 2 } \)
x = \(\\ \frac { 3 }{ 2 } \)
Question 17.
Solution:
\(\\ \frac { 9x }{ 7-6x } \) = \(\\ \frac { 15 }{ 1 } \)
By cross multiplication,
9x = 105 – 90x
=> 9x + 90x = 105
=> 99x = 105
=> x = \(\\ \frac { 105 }{ 99 } \) = \(\\ \frac { 35 }{ 33 } \)
x = \(\\ \frac { 35 }{ 33 } \)
Question 18.
Solution:
\(\\ \frac { 3x }{ 5x+2 } \) = \(\\ \frac { -4 }{ 1 } \)
By cross multiplication,
3x × 1 = – 4×(5x + 2)
=> 3x = – 20x – 8
=> 3x + 20x = – 8
=> 23x = – 8
=> x = \(\\ \frac { -8 }{ 23 } \)
Hence x = \(\\ \frac { -8 }{ 23 } \)
Question 19.
Solution:
\(\\ \frac { 6y-5 }{ 2y } \) = \(\\ \frac { 7 }{ 9 } \)
By cross multiplication,
9(6y – 5) = 7 × 2y
=> 54y – 45 = 14y
=> 54y – 14y = 45
=> 40y = 45
=> y = \(\\ \frac { 45 }{ 40 } \) = \(\\ \frac { 9 }{ 8 } \)
Hence y = \(\\ \frac { 9 }{ 8 } \) Ans.
Question 20.
Solution:
\(\\ \frac { 2-9z }{ 17-4z } \) = \(\\ \frac { 4 }{ 5 } \)
By cross multiplication,
5 (2 – 9z) = 4(17 – 4z)
=> 10 – 45z = 68 – 16z
=> – 45z + 16z = 68 – 10
=> – 29 = 58
=> z = \(\\ \frac { 58 }{ -29 } \) = – 2
Hence z = – 2 Ans.
Question 21.
Solution:
\(\\ \frac { 4x+7}{ 9-3x } \) = \(\\ \frac { 1 }{ 4 } \)
By cross multiplication,
4(4x + 7) = 1 (9 – 3x)
=> 16x + 28 = 9 – 3x
=> 16x + 3x = 9 -28
=> 19x = – 19
=> x = \(\\ \frac { -19 }{ 19 } \) = – 1
Hence x = – 1 Ans.
Question 22.
Solution:
\(\\ \frac { 7y+4}{ y+2 } \) = \(\\ \frac { -4 }{ 3 } \)
By cross multiplication,
3 (7y + 4) = – 4 (y + 2)
=> 21y + 12 = – 4y – 8
=> 21y + 4y = – 8 – 12
=> 25y = – 20
=> y = \(\\ \frac { -20 }{ 25 } \) = \(\\ \frac { -4 }{ 5 } \)
y = \(\\ \frac { -4 }{ 5 } \)
Question 23.
Solution:
\(\\ \frac { 15(2-y)-5(y+6) }{ 1-3y } \) = \(\\ \frac { 10 }{ 1 } \)
By cross multiplication,
15 (2 – y) – 5(y + 6) = 10 (1 – 3y)
=> 30 – 15y – 5y – 30 = 10 – 30y
=> – 15y – 5y + 30y = 10 – 30 + 30
=> 30y – 20y = 10
=> 10y = 10
y = \(\\ \frac { 10 }{ 10 } \) = 1
Hence y = 1 Ans.
Question 24.
Solution:
\(\\ \frac { 2x-(7-5x) }{ 9x-(3x+4x) } \) = \(\\ \frac { 7 }{ 6 } \)
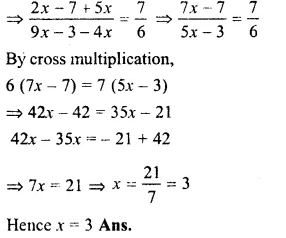
Question 25.
Solution:
\(m-\frac { \left( m-1 \right) }{ 2 } =1-\frac { \left( m-2 \right) }{ 3 } \)
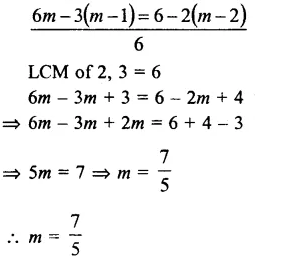
Question 26.
Solution:
\(\\ \frac { 3x+5 }{ 4x+2 } \) = \(\\ \frac { 3x+4 }{ 4x+7 } \)
By cross multiplication,
(3x + 5)(4x + 7) = (3x + 4)(4x + 2)
=> 12x² + 21x + 20x + 35
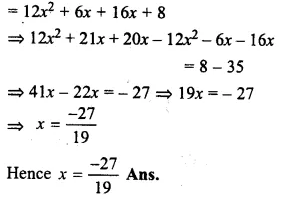
Question 27.
Solution:
\(\\ \frac { 9x-7 }{ 3x+5 } \) = \(\\ \frac { 3x-4 }{ x+6 } \)
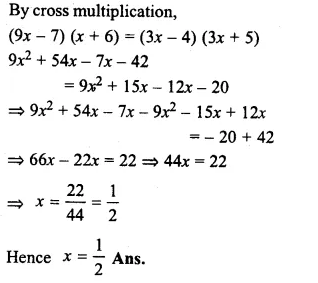
Question 28.
Solution:
\(\\ \frac { 2-7x }{ 1-5x } \) = \(\\ \frac { 3+7x }{ 4+5x } \)
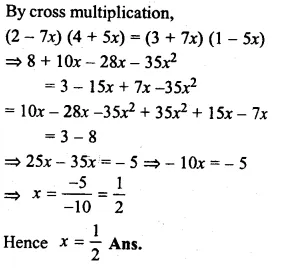
Hope given RS Aggarwal Solutions Class 8 Chapter 8 Linear Equations Ex 8A are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.