RS Aggarwal Class 9 Solutions Chapter 1 Real Numbers Ex 1D
These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1D.
Other Exercises
- RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1A
- RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1B
- RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1C
- RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1D
- RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1E
- RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1F
Question 1.
Solution:
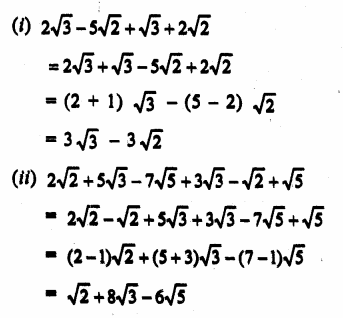
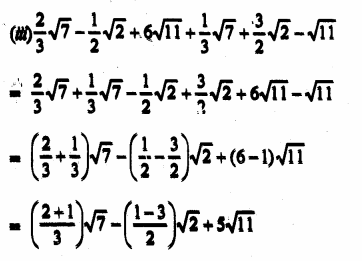
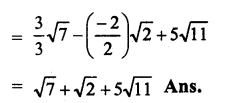
Question 2.
Solution:
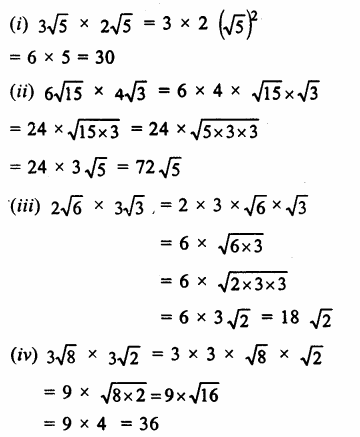
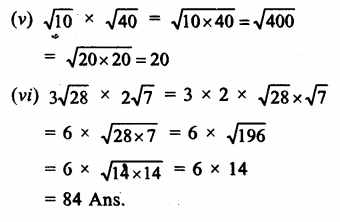
Question 3.
Solution:
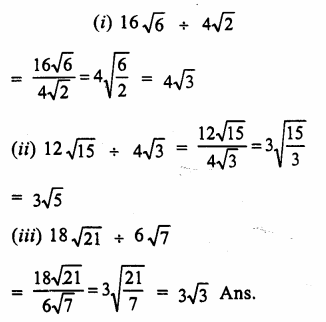
Question 4.
Solution:
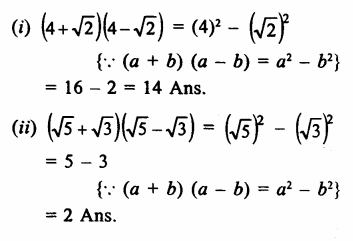
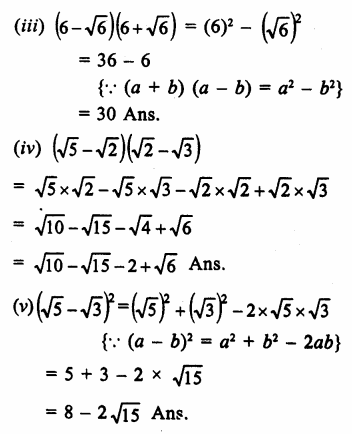
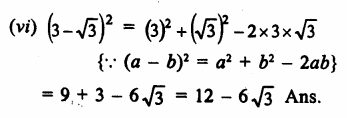
Question 5.
Solution:
(i) Draw a line segment AB = 3.2 units (cm) and extend it to C such that BC = 1 unit.
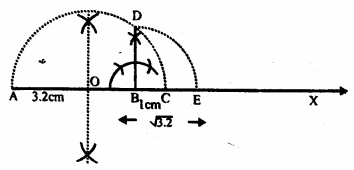
(ii) Find the mid-point O of AC.
(iii) With centre O and OA as radius draw a semicircle on AC
(iv) Draw BD ⊥ AC meeting the semicircle at D.
(v) Join BD which is √3.2 units.
(vi) With centre B and radius BD, draw an arc meeting AC when produced at E.
Then BE = BD = √3.2 units. Ans.
Question 6.
Solution:
(i) Draw a line segment AB = 7.28 units and produce is to C such that BC = 1 unit (cm)
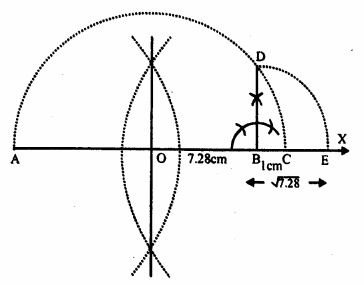
(ii) Find the mid-point O of AC.
(iii) With centre O and radius OA, draw a semicircle on AC.
(iv) Draw a perpendicular BD at AC meeting the semicircle at D
Then BD = √7.28 units.
(v) With centre B and radius BD, draw an arc which meet AC produced at E.
Then BE = BD = √7.28 units.
Question 7.
Solution:
(A) For Addition
(i) Closure property: The sum of two real numbers is always a real number.
(ii) Associative Law : (a + b) + c = a + (b + c), for all values of a, b and c.
(iii) Commutative Law : a + b = b + a for all real values of a and b.
(iv) Existance of Additive Identity : 0 is the real number such that: 0 + a = a + 0 = afor every real value of a.
(v) Existance of addtive inverse : For each real value of a, there exists a real value (-a) such that a + (-a) = (-a) + a = 0, Then (a) and (-a) are called the additive inverse of each other.
(v) Existence of Multiplicative Inverse. For each non zero real number a, there exists a real number \(\frac { 1 }{ a }\) such that a . \(\frac { 1 }{ a }\) = \(\frac { 1 }{ a }\) . a = 1
a and \(\frac { 1 }{ a }\) are called multiplicative inverse or reciprocal of each other.
(B) Multiplication
(i) Closure property: The product of two real numbers is always a real number.
(ii) Associative law : ab(c) = a(bc) for all real values of a, b and c
(iii) Commutative law : ab=ba for all real numbers a and b
(iv) Existance of Multiplicative Identity: clearly is a real number such that 1.a = a.1 = a for every value of a.
Hope given RS Aggarwal Solutions Class 9 Chapter 1 Real Numbers Ex 1D are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.