RS Aggarwal Class 9 Solutions Chapter 11 Circle Ex 11A

RS Aggarwal Class 9 Solutions Chapter 11 Circle Ex 11A

These Solutions are part of RS Aggarwal Solutions Class 9. Here we have given RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11A.

Other Exercises

• RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11A
• RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11B
• RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11C

Question 1.
Solution:
Let AB be a chord of a circle with centre O. OC⊥AB and OA be the radius of the circle, then
AB = 16cm, OA = 10cm .

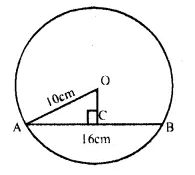
OC ⊥ AB.
OC bisects AB at C
AC = \(\frac { 1 }{ 2 } \) AB = \(\frac { 1 }{ 2 } \) x 16 = 8cm

Question 2.
Solution:
Let AB be the chord of the circle with centre O and OC ⊥ AB, OA be the radius of the circle,
then OC = 3cm, OA = 5cm

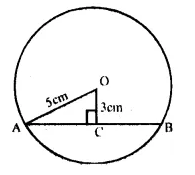
Now in right ∆ OAC,
OA² = AC² = OC² (Pythagoras Theorem)

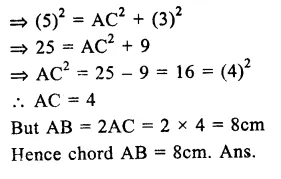
Question 3.
Solution:
Let AB be the chord, OA be the radius of
the circle OC ⊥ AB
then AB = 30 cm, OC = 8cm

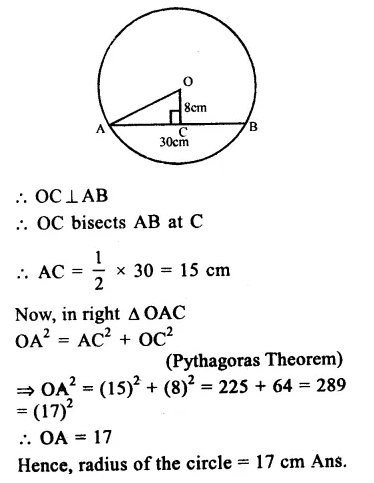
Question 4.
Solution:
AB and CD are parallel chords of a circle with centre O.

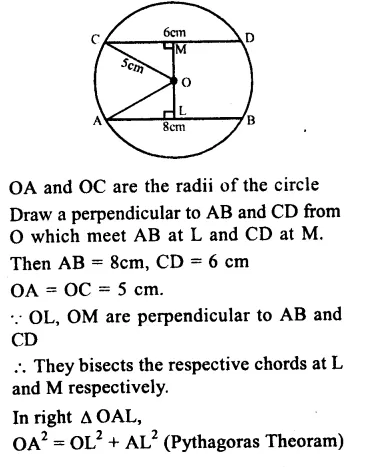
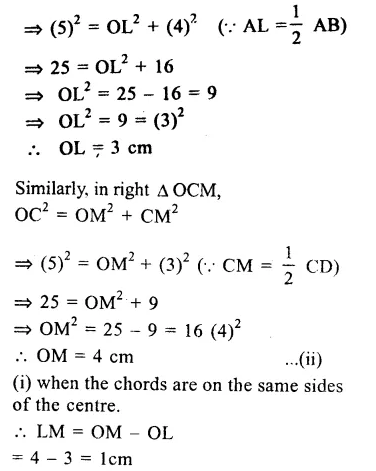
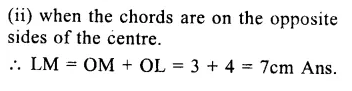
Question 5.
Solution:
Let AB and CD be two chords of a circle with centre O.
OA and OC are the radii of the circle. OL⊥AB and OM⊥CD.

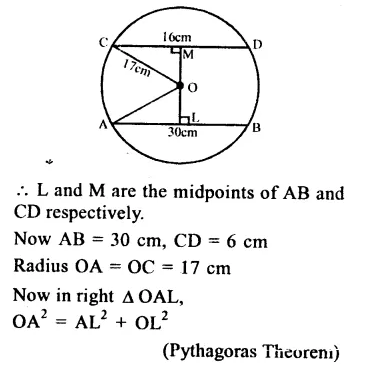
Question 6.
Solution:
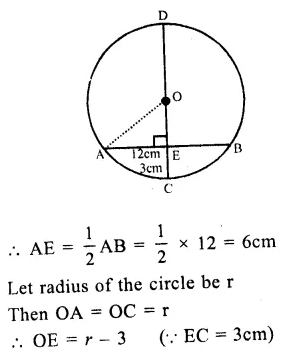
In the figure, a circle with centre O, CD is its diameter AB is a chord such that CD⊥AB.
AB = 12cm, CE = 3cm.
Join OA.
∵ COD⊥AB which intersects AB at E

Question 7.
Solution:
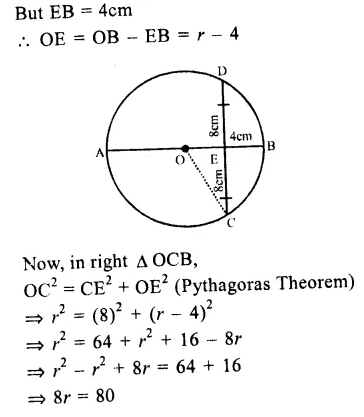
A circle with centre O, AB is diameter which bisects chord CD at E
i.e. CE = ED = 8cm and EB = 4cm
Join OC.
Let radius of the circle = r

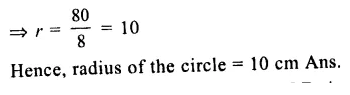
Question 8.
Solution:
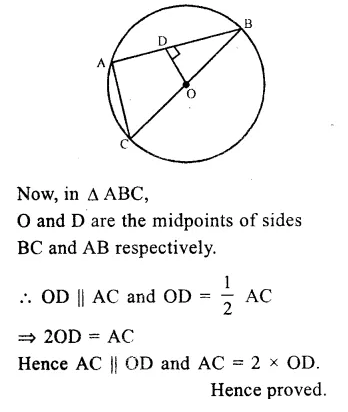
Given : O is the centre of a circle AB is a chord and BOC is the diameter. OD⊥AB
To prove : AC || OD and AC = 20D
Proof : OD⊥AB
∵ D is midpoint of AB

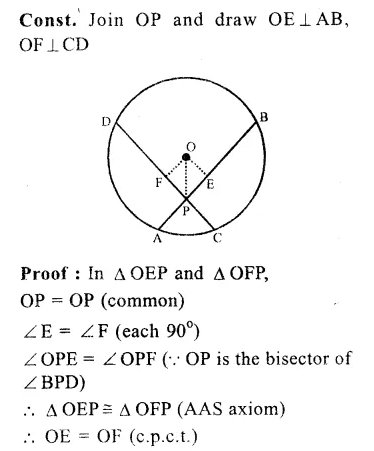
Question 9.
Solution:
Given : O is the centre of the circle two
chords AB and CD intersect each other at P inside the circle. PO bisects ∠BPD.
To prove : AB = CD.

Question 10.
Solution:
Given : PQ is the diameter of the circle with centre O which is perpendicular to one chord AB and chord AB || CD.
PQ intersects AB and CD at E and F respectively
To prove : PQ⊥CD and PQ bisects CD.

Question 11.
Solution:
Two circles with centre O and O’ intersect each other.

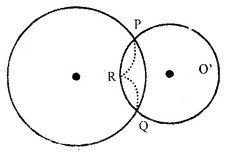
To prove : The two circles cannot intersect each other at more than two points.
Proof : Let if opposite, the two circles intersect each other at three points P, Q and R.
Then these three points are non-collinear. But, we know that through three non- collinear points, one and only one circle can be drawn.
∵ Our supposition is wrong
Hence two circle can not intersect each other at not more than two points.
Hence proved

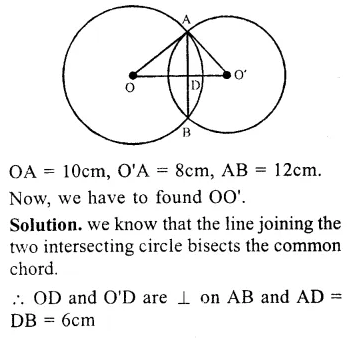
Question 12.
Solution:
Given : Two circles with centres O and O’ intersect each other at A and B. AB is a common chord. OO’ is joined.
AO and AO is joined.

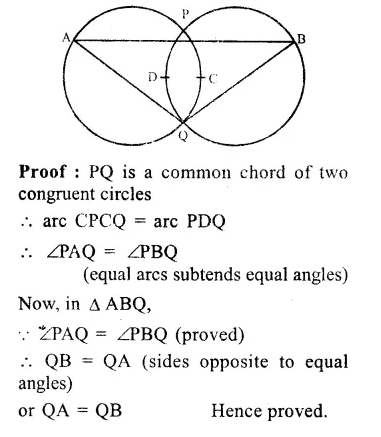
Question 13.
Solution:
Given : Two equal circles intersect each other at P and Q.
A straight line drawn through
P, is drawn which meets the circles at A and B respectively
To prove : QA = QB

Question 14.
Solution:
Given : A circle with centre 0. AB and CD are two chords and diameter PQ bisects AB and CD at L and M
To Prove : AB || CD.

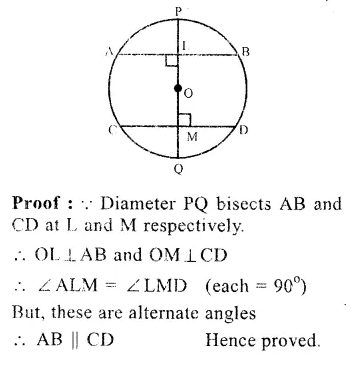
Question 15.
Solution:
Given : Two circles with centres A and B touch each other at C internally. A, B arc joined. PQ is the perpendicular bisector of AB intersecting it at L and meeting the bigger circle at P and Q respectively and radii of the circles are 5cm and 3cm. i.e. AC = 5cm,BC = 3cm
Required : To find the lenght of PQ

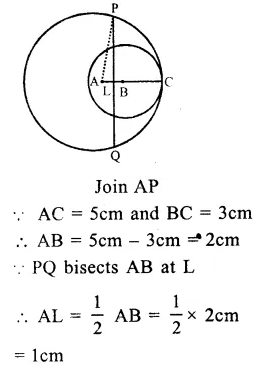
Question 16.
Solution:
Given : AB is a chord of a circle with centre O. AB is produced to C such that BC = OB, CO is joined and produced to meet the circle at D.
∠ ACD = y°, ∠ AOD = x°
To prove : x = 3y

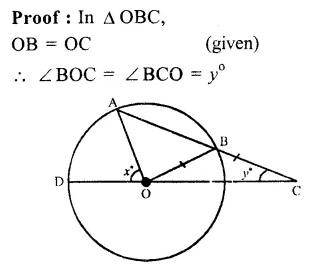
Question 17.
Solution:
Given : O is the centre of a circle AB and AC are two chords such that AB = AC
OP⊥AB and OQ⊥AC.
which intersect AB and AC at M and N
respectively. PB and QC are joined.
To prove : PB = QC.

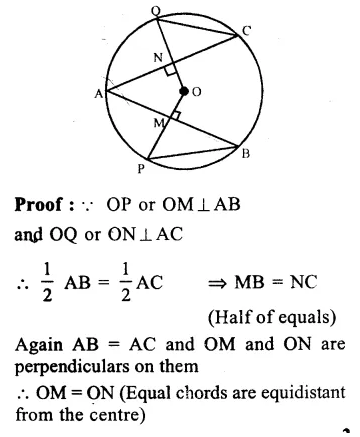
Question 18.
Solution:
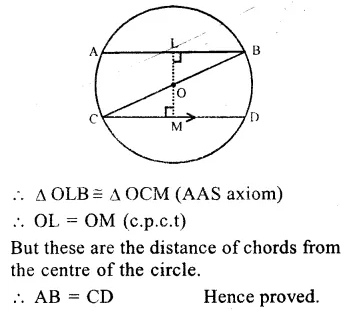
Given : In a circle with centre O, BC is its diameter. AB and CD are two chords such that AB || CD.
To prove : AB = CD
Const. Draw OL⊥AB
OM⊥CD.
Proof : In ∆ OLB and ∆ OCM,
OB = OC (radii of the same circle)
∠ OLB = ∠ OMC (each 90°)
∠ OBL = ∠ OCM (alternate angles)

Question 19.
Solution:
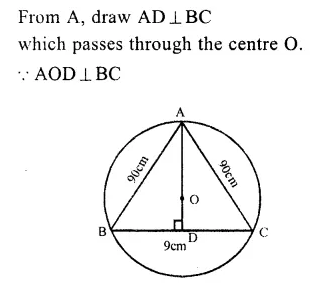
Equilateral ∆ ABC in inscribed in a circle in which
AB = BC = CA = 9cm.

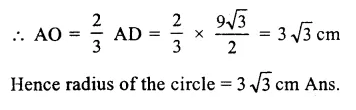
Question 20.

Solution:
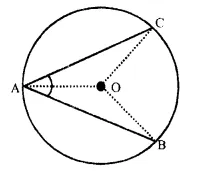
Given : AB and AC are two equal chords of a circle with centre O
To Prove : O lies on the bisector of ∠ BAC

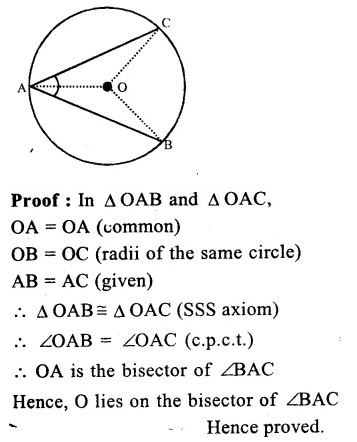
Question 21.
Solution:
Given : OPQR is a square with centre O, a circle is drawn which intersects the square at X and Y.
To Prove : Q = QY
Const. Join OX and OY

 

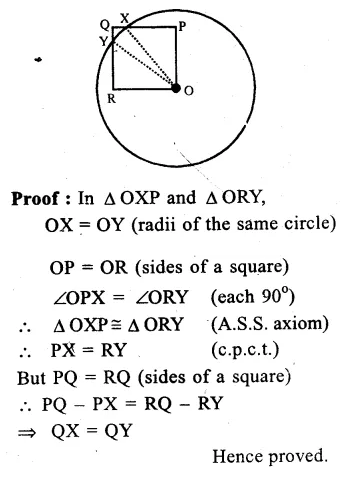
Hope given RS Aggarwal Solutions Class 9 Chapter 11 Circle Ex 11A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.