RS Aggarwal Solutions Class 10 Chapter 17 Perimeter and Areas of Plane Figures Ex 17b
These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 17 Perimeter and Areas of Plane Figures Ex 17b.
Other Exercises
- RS Aggarwal Solutions Class 10 Chapter 17 Perimeter and Areas of Plane Figures Ex 17A
- RS Aggarwal Solutions Class 10 Chapter 17 Perimeter and Areas of Plane Figures Ex 17B
- RS Aggarwal Solutions Class 10 Chapter 17 Perimeter and Areas of Plane Figures MCQ
- RS Aggarwal Solutions Class 10 Chapter 17 Perimeter and Areas of Plane Figures Test Yourself
Question 1.
Solution:
Let the length of plot be x meters
Its perimeter = 2 [length + breadth]
= 2(x + 16) = (2x + 32) meters
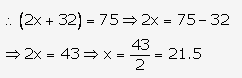
Length of the rectangle is 21. 5 meter
Area of the rectangular plot = length × breadth
= (16 × 21.5)m2
= 344 m2
The length = 21.5 m and the area = 344 m2
Question 2.
Solution:
The length of a rectangular park is twice its breadth
and its perimeter is 840 m.
Find the area of the park.
Let the breadth of a rectangular park = x m
Then, length of a rectangular park = 2x m
Perimeter of a rectangular park = 840 m
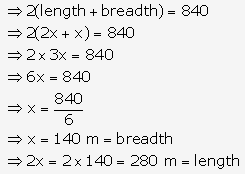
∴ Area of a rectangular park = length x breadth = 140x 280 = 39200 m2
Question 3.
Solution:
Let ABCD be the rectangle in which AB = 12 cm and AC = 37 m
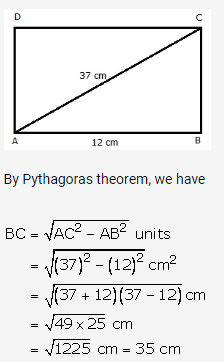
Thus, length = 35 cm and breadth = 12 cm
Area of rectangle = (12 × 35) = 420
Hence, the other side = 35 cm and the area = 420 cm2
Question 4.
Solution:
Let the breadth of the plot be x meter
Area = Length × Breadth = (28 × x) meter
= 28x m2
Breadth of plot is = 16. 5 m
Perimeter of the plot is = 2(length + breadth)

Question 5.
Solution:

Question 6.
Solution:

Question 7.
Solution:

Question 8.
Solution:
Area of verandah = (36 × 15)m2 = 540 m2
Area of stone = (0.6 × 0.5)m2 [10 dm = 1 m]
Number of stones required = \(\frac { Area\quad of\quad verandah }{ Area\quad of\quad stone } =\frac { 540 }{ 0.3 } =1800\)
Hence, 1800 stones are required to pave the verandah
Question 9.
Solution:

Question 10.
Solution:
Length of the park = 35 m
Breadth of the park = 18 m
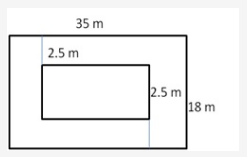
Area of the park = (35 18)m2 = 630 m2
Length of the park with grass =(35 – 5) = 30 m
Breadth of the park with grass = (18 – 5) m = 13 m
Area of park with grass = (30 × 13) m2 = 390 m2
Area of path without grass = Area of the whole park area of park with grass
= 630 m2 – 390 m2 = 240 m2
Hence, area of the park to be laid with grass = 240 m2
Question 11.
Solution:
Length of the plot = 125 m
Breadth of the plot = 78 m
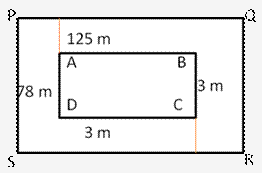
Area of plot ABCD = (125 × 78)m2 = 9750 m2
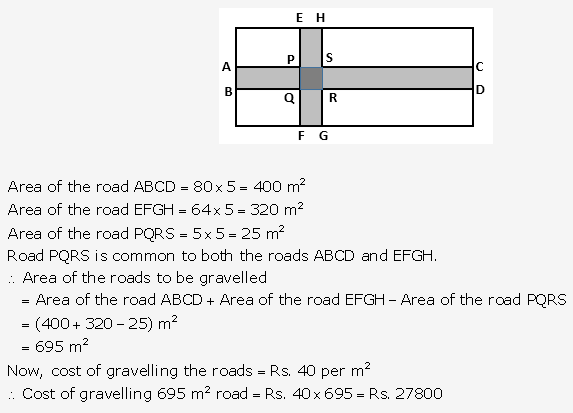
Length of the plot including the path= (125 + 3 + 3) m = 131 m
Breadth of the plot including the path = (78 + 3 + 3) m = 84 m
Area of plot PQRS including the path
= (131 × 84) m2 = 11004 m2
Area of path = Area of plot PQRS Area of plot ABCD
= (11004 – 9750)m2 = 1254 m2
Cost of gravelling = Rs 75 per m2
Cost of gravelling the whole path = Rs. (1254 × 75) = Rs. 94050
Hence, cost of gravelling the path = Rs. 94050.
Question 12.
Solution:
Area of rectangular field including the foot path = (54 × 35)m2
Let the width of the path be x m
Then, area of rectangle plot excluding the path = (54 × 2x) (35 × 2x)
Area of path = (54 × 35) (54 × 2x) (35 × 2x) = 54 ×35) (54 × 2x) (35 × 2x) = 420
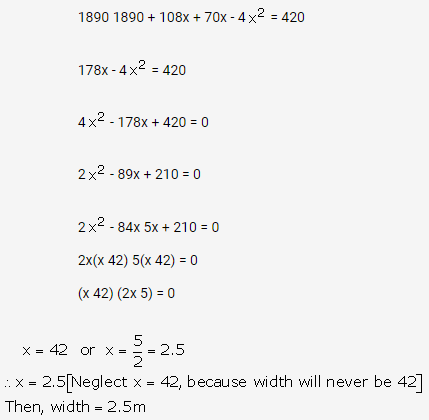
Question 13.
Solution:
Let the length and breadth of a rectangular garden be 9x and 5x.
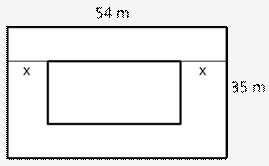
Then, area of garden = (9x 5x)m = 45x2 m2
Length of park excluding the path = (9x 7) m
Breadth of the park excluding the path = (5x 7) m
Area of the park excluding the path = (9x 7)(5x 7) m2
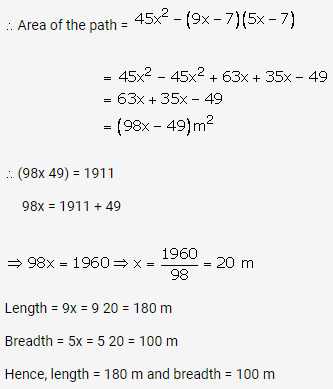
Question 14.
Solution:

Question 15.
Solution:
Let the width of the carpet = x meter
Area of floor ABCD = (8 ×5) m2
Area of floor PQRS without border
= (8 × 2x)(5 × 2x)
= 40 × 16 x 10x + 4x2
= 40 × 26x + 4x2
Area of border = Area of floor ABCD Area of floor PQRS
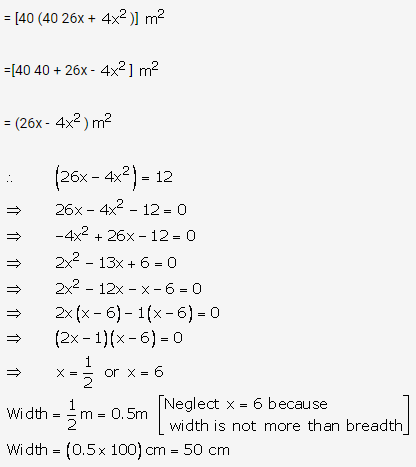
Question 16.
Solution:
Question 17.
Solution:

Question 18.
Solution:

Question 19.
Solution:
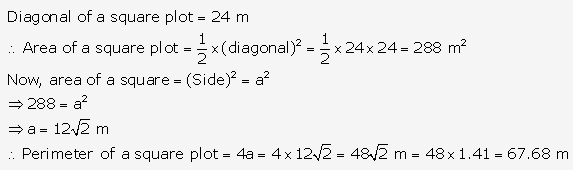
Question 20.
Solution:

Question 21.
Solution:

Question 22.
Solution:

Question 23.
Solution:

Question 24.
Solution:
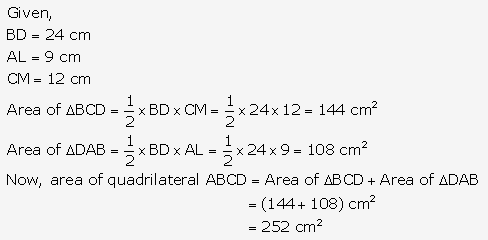
Question 25.
Solution:


Question 26.
Solution:

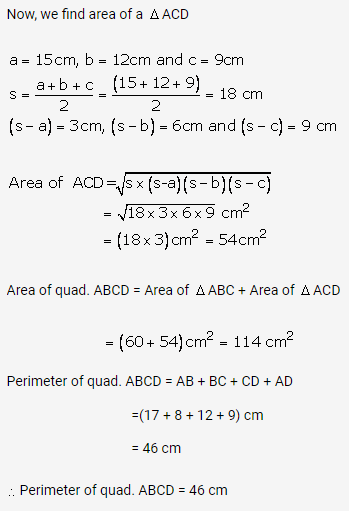
Question 27.
Solution:
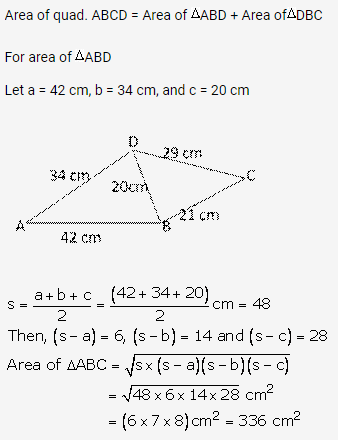

Question 28.
Solution:
Area of the ||gm = (base height) sq. unit
= (25 × 16.8) cm2 = 420 cm2
Question 29.
Solution:

Question 30.
Solution:

Question 31.
Solution:
Area of parallelogram = 2 area of DABC
Opposite sides of parallelogram are equal
AD = BC = 20 cm
And AB = DC = 34 cm
In ∆ABC we have
a = AC = 42 cm
b = AB = 34 cm
c = BC = 20 cm

Question 32.
Solution:
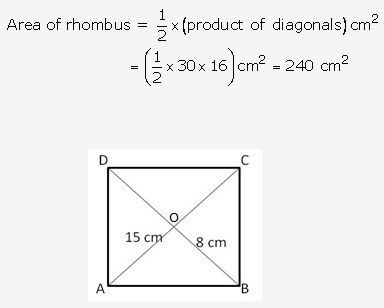
We know that the diagonals of a rhombus, bisect each other at right angles
OA = OC = 15 cm,
And OB = OD = 8 cm
And ∠AOB = 900
∴By Pythagoras theorem, we have
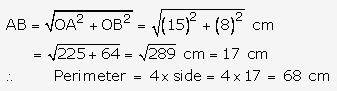
Question 33.
Solution:
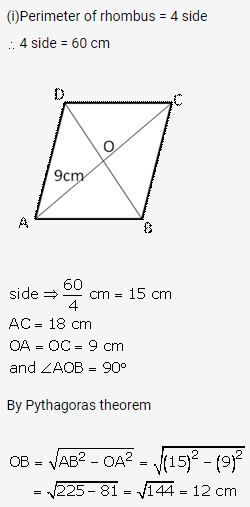

Question 34.
Solution:
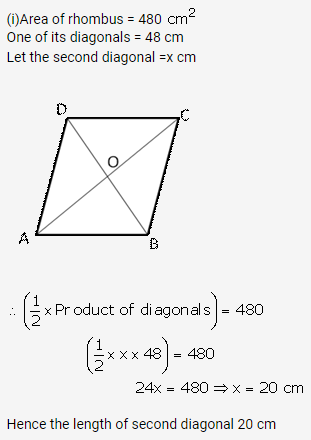

Question 35.
Solution:
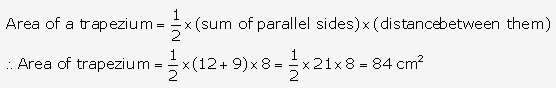
Question 36.
Solution:

Question 37.
Solution:
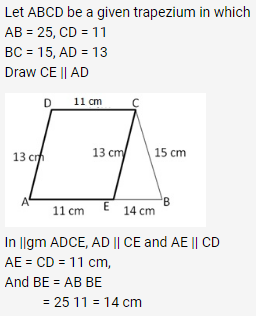

Hope given RS Aggarwal Solutions Class 10 Chapter 17 Perimeter and Areas of Plane Figures Ex 17b are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.