RS Aggarwal Solutions Class 10 Chapter 6 T-Ratios of Some Particular Angles Ex 6

RS Aggarwal Solutions Class 10 Chapter 6 T-Ratios of Some Particular Angles Ex 6

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 6 T-Ratios of Some Particular Angles Ex 6.

Other Exercises

• RS Aggarwal Solutions Class 10 Chapter 6 T-Ratios of Some Particular Angles Ex 6

Question 1.
Solution:
On substituting the value of various T-ratios, we get
sin60° cos30° + cos60° sin30°

Question 2.
Solution:
On substituting the value of various T-ratios, we get
cos60° cos30° – sin60° sin30°

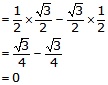
Question 3.
Solution:
On substituting the value of various Tratios, we get
cos45° cos30° + sin45° sin30°

Question 4.
Solution:
On substituting the value of various Tratios, we get

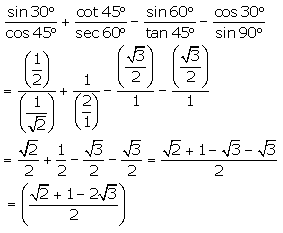
Question 5.
Solution:

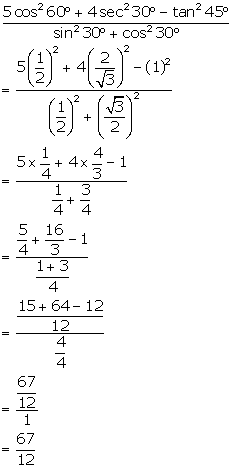
Question 6.
Solution:
On substituting the value of various Tratios, we get

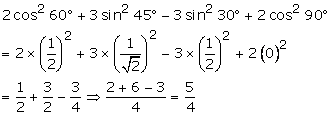
Question 7.
Solution:
On substituting the value of various Tratios, we get

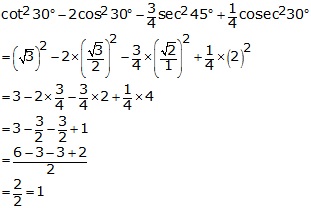
Question 8.
Solution:
On substituting the value of various Tratios, we get

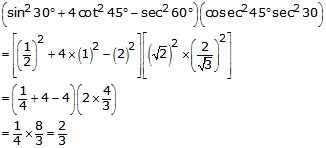
Question 9.
Solution:
On substituting the value of various Tratios, we get

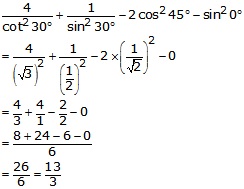
Question 10.
Solution:
(i)

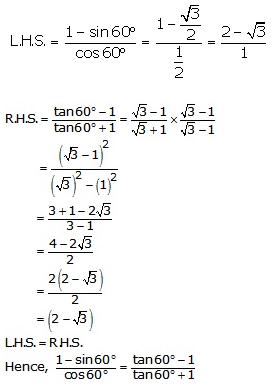
(ii)

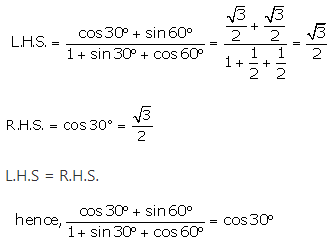
Question 11.
Solution:
(i)

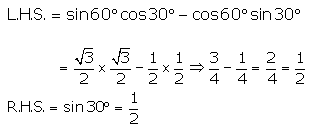
R.H.S. = L.H.S.
Hence, sin60° cos30° – cos60° sin30° = sin30°

(ii)
L.H.S. = cos60° cos30° + sin60° sin30°

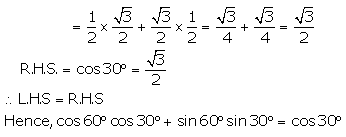
(iii)

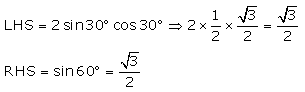
R.H.S. = L.H.S.
Hence,2sin30° cos30° = sin60°

(iv)

R.H.S. = sin90° = 1
R.H.S. = L.H.S.
Hence, 2 sin 45° cos45° = sin90°

Question 12.
Solution:
A = 45° 2 A = 90°

(i)Sin 2A = sin90° = 1

(ii) cos2A = cos90° = 0

Question 13.
Solution:
A = 30 ⇒ 2A = 60

(i)

(ii)

(iii)

Question 14.
Solution:
(i)

(ii)

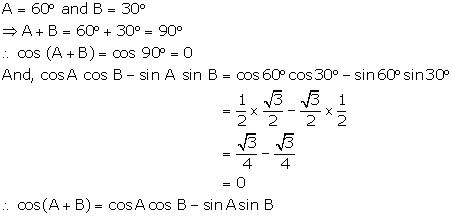
Question 15.
Solution:
(i)

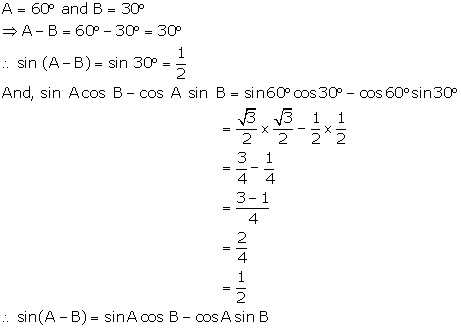
(ii)

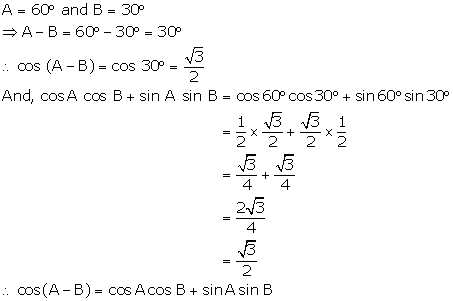
(iii)

Question 16.
Solution:

Hence, (A + B) = 45

Question 17.
Solution:
Putting A = 30° 2 A = 60°

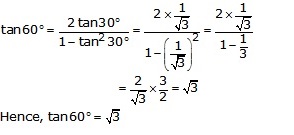
Question 18.
Solution:
Putting A = 30° 2 A = 60°

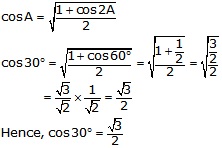
Question 19.
Solution:
Putting A = 30° 2 A = 60°

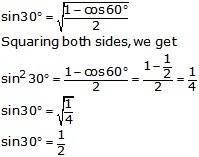
Question 20.
Solution:
From right angled ∆ABC,

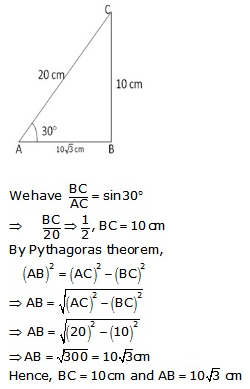
Question 21.
Solution:
From right angled ∆ABC,

Question 22.
Solution:
From right angled  ∆ABC,

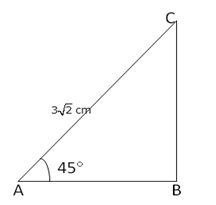
(i)

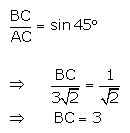
(ii)
By Pythagoras theorem

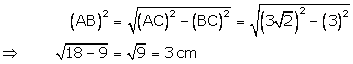
Hence, (i) BC = 3cm and (ii) AB = 3cm.

Question 23.
Solution:
sin (A + B)= 1  sin (A + B) = sin90°

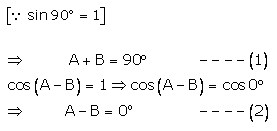
Adding (1) and (2), we get
2A = 90° ⇒ A = 45°
Putting A = 45° in (1) we get
45° + B = 90° ⇒ B = 45°
Hence, A = 45° and B = 45°.

Question 24.
Solution:

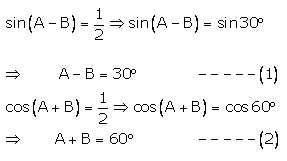
Solving (1) and (2), we get
2A = 90° ⇒ A = 45°
Putting A = 45° in (1), we get
45° – B = 30° ⇒ B = 45 – 30° = 15°
Hence, A = 45°, B = 15°.

Question 25.
Solution:

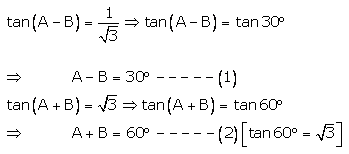
Solving (1) and (2), we get
2A = 90° ⇒ A = 45°
Putting A = 45° in (1), we get
45° – B = 30° ⇒ B = 45° – 30°  = 15°
A = 45°, B = 15°

Question 26.
Solution:

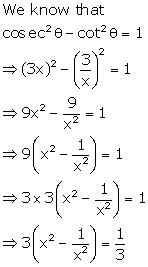
Question 27.
Solution:

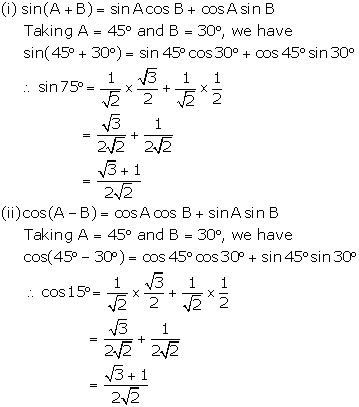
We hope the RS Aggarwal Solutions Class 10 Chapter 6 T-Ratios of Some Particular Angles Ex 6 help you. If you have any query regarding RS Aggarwal Solutions Class 10 Chapter 6 T-Ratios of Some Particular Angles Ex 6, drop a comment below and we will get back to you at the earliest.