RS Aggarwal Solutions Class 10 Chapter 9 Mean, Median, Mode of Grouped Data,Cumulative Frequency Graph and O give MCQ

These Solutions are part of RS Aggarwal Solutions Class 10. Here we have given RS Aggarwal Solutions Class 10 Chapter 9 Mean, Median, Mode of Grouped Data,Cumulative Frequency Graph and O give MCQ.

Other Exercises

Question 1.
Solution:
Correct option: (d)
Range is not a measure of central tendency.

Question 2.
Solution:
Correct option: (a)
Mean cannot be determined graphically.

Question 3.
Solution:
Correct option: (a)
Since mean is the average of all observations, it is influenced by extreme values.

Question 4.
Solution:
Correct option: (c)
Mode can be obtained graphically from a histogram.

Question 5.
Solution:
Correct option: (d)
Ogives are used to determine the median of a frequency distribution.

Question 6.
Solution:
Correct option: (b)
The cumulative frequency table is useful in determining the median.

Question 7.
Solution:
Correct option: (b)
Median is given by the abscissa of the point of intersection of the Less than Type and More than Type cumulative frequency curves.

Question 8.
Solution:
Correct option: (b)
For a grouped data,
\(\sum { f }_{ i }\left( { x }_{ i }-\bar { x } \right) =0\)

Question 9.
Solution:
Correct option: (b)
By formula method,
\(\bar { x } =\quad A+h\left[ \frac { \sum { { f }_{ i }{ u }_{ i } } }{ \sum { { f }_{ i } } } \right] \)
where \({ u }_{ i }=\quad \frac { \left( { x }_{ i }-A \right) }{ h } \)

Question 10.
Solution:
Correct option: (c)
di‘s are the deviations from A of midpoints of the classes.

Question 11.
Solution:
Correct option: (b)
While computing the mean of the grouped data, we assume that the frequencies are centred at the class marks of the classes.

Question 12.
Solution:
Correct option: (b)
Mode = (3 x median) – (2 x mean)

Question 13.
Solution:
Correct option: (c)
Since the abscissa of the point of intersection of both the ogives gives the median, we have median = 20.5

Question 14.
Solution:
RS Aggarwal Solutions Class 10 Chapter 9 Mean, Median, Mode of Grouped Data MCQ 1

Question 15.
Solution:
Correct option: (c)
Class having maximum frequency is the modal class.
Here, maximum frequency = 30
Hence, the modal class is 30 – 40.

Question 16.
Solution:
Correct option: (b)
Mode = \({ x }_{ k }+h.\left\{ \frac { { f }_{ k }-{ f }_{ k-1 } }{ \left( { 2f }_{ k }-{ f }_{ k-1 }-{ f }_{ k+1 } \right) } \right\} \)

Question 17.
Solution:
Correct option: (a)
Median = \(l+\left\{ h\times \frac { \left( \frac { N }{ 2 } -cf \right) }{ f } \right\} \)

Question 18.
Solution:
Correct option: (c)
Mean = 8.9
Median = 9
Mode = 3Median – 2Mean
= 3 x 9 – 2 x 8.9
= 27 – 17.8
= 9.2.

Question 19.
Solution:
RS Aggarwal Solutions Class 10 Chapter 9 Mean, Median, Mode of Grouped Data MCQ 2

Question 20.
Solution:
RS Aggarwal Solutions Class 10 Chapter 9 Mean, Median, Mode of Grouped Data MCQ 3

Question 21.
Solution:
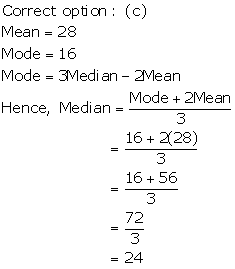
RS Aggarwal Solutions Class 10 Chapter 9 Mean, Median, Mode of Grouped Data MCQ 4

Question 22.
Solution:
RS Aggarwal Solutions Class 10 Chapter 9 Mean, Median, Mode of Grouped Data MCQ 5

Question 23.
Solution:
Correct option: (c)
For a symmetrical distribution,
we have  Mean = mode = median

Question 24.
Solution:
Correct option: (c)
Number of families having income more than Rs. 20000 = 50
Number of families having income more than Rs. 25000 = 37
Hence, number of families having income range 20000 to 25000 = 50 – 37 = 13

Question 25.
Solution:
RS Aggarwal Solutions Class 10 Chapter 9 Mean, Median, Mode of Grouped Data MCQ 6

Question 26.
Solution:
Correct option: (d)
Mean of 20 numbers = 0
Hence, sum of 20 numbers = 0 x 20 = 0
Now, the mean can be zero if
sum of 10 numbers is (S) and the sum of remaining 10 numbers is (-S),
sum of 11 numbers is (S) and the sum of remaining 9 numbers is (-S), …….
sum of 19 numbers is (S) and the 20th number is (-S), then their sum is zero.
So, at the most, 19 numbers can be greater than zero.

Question 27.
Solution:
RS Aggarwal Solutions Class 10 Chapter 9 Mean, Median, Mode of Grouped Data MCQ 7

Question 28.
Solution:
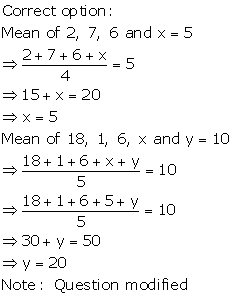
RS Aggarwal Solutions Class 10 Chapter 9 Mean, Median, Mode of Grouped Data MCQ 8

Question 29.
Solution:
(a) – (s)
The most frequent value in a data is known as mode.
(b) – (r)
Mean cannot be determined graphically.
(c) – (q)
An ogive is used to determine median.
(d) – (p)
Standard deviation is not a measure of central tendency.

Question 30.
Solution:
RS Aggarwal Solutions Class 10 Chapter 9 Mean, Median, Mode of Grouped Data MCQ 9

Question 31.
Solution:
RS Aggarwal Solutions Class 10 Chapter 9 Mean, Median, Mode of Grouped Data MCQ 10

We hope the RS Aggarwal Solutions Class 10 Chapter 9 Mean, Median, Mode of Grouped Data MCQ help you. If you have any query regarding RS Aggarwal Solutions Class 10 Chapter 9 Mean, Median, Mode of Grouped Data MCQ, drop a comment below and we will get back to you at the earliest.