Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14A

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14A.

Other Exercises

Question 1.
Find, which of the following points lie on the line x – 2y + 5 = 0 :
(i) (1, 3)
(ii) (0, 5)
(iii) (-5, 0)
(iv) (5, 5)
(v) (2, -1.5)
(vi) (-2, -1.5)
Solution:
Equation of given line x – 2y + 5 = 0
(i) Substituting x = 1, y = 3, in the given equation.
1 – 2 x 3 + 5 = 0 ⇒ 1 – 6 + 5 = 0 ⇒ 0 = 0, which is true.
(1, 3) satisfies the equation.
(ii) Substituting x = 0 , y = 5 in the given equation
0 – 2 x 5 + 5 = 0 ⇒ 0 – 10 + 5 = 0 ⇒ -5 = 0, which is not true.
( 0, 5) does not satisfy the equation.
(iii) Substituting x = – 5, y = 0 in the given equation
-5 – 2 x 0 + 5 = 0 ⇒ -5 – 0 + 5 = 0 ⇒ 0 = 0 which is true.
(-5, 0) satisfies the equation.
(iv) Substituting x = 5, y = 5 in the given equation.
– 5 – 2 x 5 + 5 = 0 ⇒ -5 – 10 + 5 = 0 ⇒ 0 = 0 which is true.
(5, 5) satisfies the equation.
(v) Substituting x = 2, y = -1.5 in the given equation.
2 – 2 x (- 1.5) + 5 = 0 ⇒ 2 + 3 + 5 = 0 ⇒ 10 = 0. which is not true.
(2, -1.5) does not satisfy the equation.
(vi) Substituting x = -2, y = -1.5 in the given equation
– 2 – 2 x (-1.5) + 5 = 0 ⇒ – 2 + 3 + 5 = 0 ⇒ 6 = 0, which is not true.
(-2, -1.5) does not satisfies the equation.

Question 2.
State, true or false :
(i) the line \(\frac { x }{ 2 }\) + \(\frac { y }{ 3 }\) = 0 passes through the point (2, 3).
(ii) the line \(\frac { x }{ 2 }\) + \(\frac { y }{ 3 }\) = 0 passes through the point (4, -6).
(iii) the point (8, 7) lies on the line y – 7 = 0
(iv) the point (-3, 0) lies on the line x + 3 = 0
(v) if the point (2, a) lies on the line 2x – y = 3, then a = 5.
Solution:
(i) Equation of the line is \(\frac { x }{ 2 }\) + \(\frac { y }{ 3 }\) = 0
and co-ordinates of point are (2, 3)
If the point is on the line, then it will satisfy the equation.
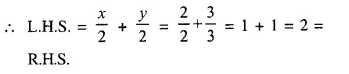
Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14A Q2.1
(2, 3) is not on the line
(ii) Equation of the line is \(\frac { x }{ 2 }\) + \(\frac { y }{ 3 }\) = 0
and co-ordinates of point are (4, -6)
If the point is on the line, then it will satisfy the equation
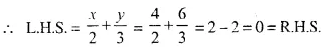
Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14A Q2.2
Hence, point (4, -6) is on the line.
(iii) Equation of line is y – 7 = 0 and the co-ordinates of point are (8, 7)
If the point is on the line, then it will satisfy the equation
L.H.S. = y – 7 = 7 – 7 = 0 = R.H.S.
Hence, point (8, 7) is on the line.
(iv) Equation of the line is x + 3 = 0 and co-ordinates of point are (-3, 0)
If the point is on the line, then it will satisfy the equation.
L.H.S. = x + 3 = -3 + 3 = 0 = R.H.S.
Hence, the point (-3, 0) is on the line.
(v) Equation of the line is 2x – y = 3
and co-ordinates of the point are (2, a)
If the point is on the line, then it will satisfy the equation.
L.H.S. = 2x – y = 2 x 2 – a = 4 – a
R.H.S. = 3
4 – a = 3 ⇒ 4 + 3 = a ⇒ a = 7
But a = 5 given, therefore it is not on the line.
(i) False (ii) True (iii) True (iv) True (v) False.

Question 3.
The line given by the equation 2x – \(\frac { y }{ 3 }\) = 7 passes through the point (k, 6); calculate the value of k.
Solution:
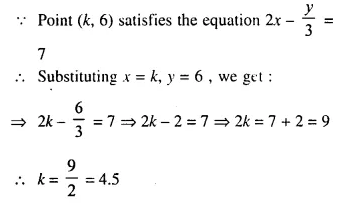
Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14A Q3.1

Question 4.
For what value of k will the point (3, -k) lie on the line 9x + 4y = 3 ?
Solution:
Point (3, -k) satisfies the equation 9x + 4y = 3
Substituting x = 3 , y = -k, we get :
9 x 3 + 4 (- k), = 3
⇒ 27 – 4k = 3
⇒ – 4k = 3 – 27
⇒ – 4k = – 24
⇒ k = 6

Question 5.
The line \(\frac { 3x }{ 5 }\) – \(\frac { 2y }{ 3 }\) + 1 = 0, contains the point (m, 2m – 1); calculate the value of m.
Solution:
Point (m, 2m -1) satisfies the equation
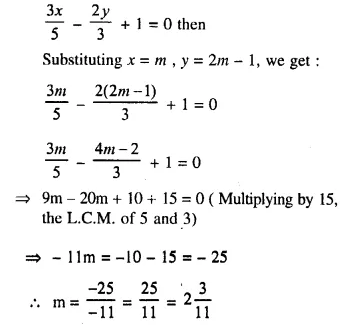
Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14A Q5.1

Question 6.
Does the line 3x – 5y = 6 bisect the join of (5, -2) and (-1, 2) ?
Solution:
Line 3x – 5y = 6 bisect the join of points (5, -2) and (-1, 2)
The mid-point of (5, -2) and (-1, 2) satisfies the equation.
Now, mid-point of (5, -2) and (-1, 2)
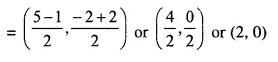
Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14A Q6.1
Now, substituting x = 2, y = 0, in the given equation
3 x 2 – 5 x 0 = 6 ⇒ 6 – 0 = 6 ⇒ 6 = 6 which is true. .
Given line bisect the join of points (5, -2) and (-1, 2)

Question 7.
(i) The line y = 3x – 2 bisects the join of (a, 3) and (2, -5), find the value of k.
(ii) The line x – 6y + 11 = 0 bisects the join of (8, -1) and ( 0, k). Find the value of k.
Solution:
(i) line y = 3x – 2 bisects the join of (a, 3) and (2, -5)
Mid-point join of there points satisfies it.
Now, mid-point of (a, 3) and (2, -5) is
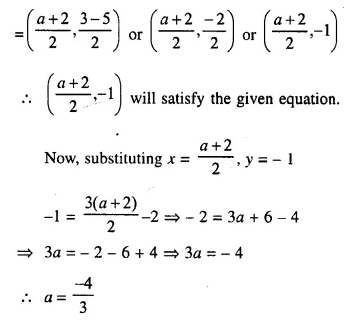
Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14A Q7.1
Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14A Q7.2
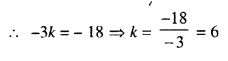
Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14A Q7.3

Question 8.
(i) The point (-3, -2) lies on the line ax + 3y + 6 = 0, calculate the value of ‘a’
(ii) The line y = mx + 8 contains the point (- 4, 4), calculate the value of ‘m’
Solution:
(i) Point (-3, 2) lies on the line ax + 3y + 6 = 0,
Then x = – 3, y = 2 satisfies it
a (-3) + 3(2) + 6 = 0
⇒ -3a + 6 + 6 = 0
⇒ -3a + 12 = 0
⇒ -3a = – 12
⇒ a = 4
(ii) line y = mx + 8 contains the point (-4, 4)
x = – 4, y = 4 satisfies it
4 = m (-4) + 8
⇒ 4 = -4m + 8
⇒ 4m = 8 – 4 = 4
⇒ m = 1

Question 9.
The point P divides the join of (2, 1) and (-3, 6) in the ratio 2 : 3. Does P lie on the line x – 5y + 15 = 0 ?
Solution:
P divides the line joining of the points (2, 1) and (-3, 6) in the ratio of 2 : 3,
co-ordinates of P will be
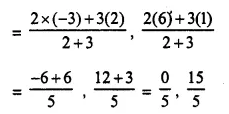
Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14A Q9.1
Now, substituting x = 0, y = 3 in the equation
x – 5y + 15 = 0
⇒ 0 – 5 x 3 + 15 = 0
⇒ 0 – 15 + 15 = 0
⇒ 0 = 0 which is true.
Point (0, 3) lies on the line.

Question 10.
The line segment joining the points (5, -4) and (2, 2) is divided by the point Q in the ratio of 1 : 2. Does the line x – 2y = 0 contain Q ?
Solution:
Point Q, divides the line segment joining the points (5, -4) and (2, 2) in the rates of 1 : 2
co-ordinates of Q will be,
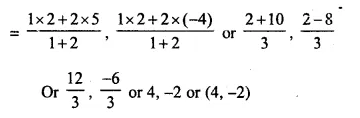
Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14A Q10.1
Now, substituting x = 4, y = – 2 in the equation
x – 2y = 0, we get
4 – 2 x (-2) = 0
⇒ 4 + 4 = 0
⇒ 8 = 0 which is not true.
Point Q does not lie on the line x – 2y = 0

Question 11.
Find the point of intersection of the lines : 4x + 3y = 1 and 3x – y + 9 = 0. If this point lies on the line (2k – 1) x – 2y = 4; find the value of k.
Solution:
4x + 3y = 1 …..(i)
3x – y = -9 …..(ii).
Multiplying (i) by 1 and (ii) 3
4x + 3y = 1
9x – 3y = -27
Adding, we get-:
1 3x = – 26 ⇒ x = -2
from (ii),
3x – y = – 9
3(-2) – y = -9
⇒ – 6 – y = -9
⇒ -y = -9 + 6 = -3
⇒ y = 3
The point of intersection is (-2, 3)
The line (2k – 1) x – 2y = 4 passes through that point also
It is satisfy it.
(2k – 1) (-2) – 2(3) = 4
⇒ -4k + 2 – 6 = 4
⇒ -4k – 4 = 4
⇒ -4k = 4 + 4 = 8
⇒ k = -2
Hence point of intersection is (-2, 3) and value of k = -2

Question 12.
Show that the lines 2x + 5y = 1, x – 3y = 6 and x + 5y + 2 = 0 are concurrent.
Solution:
2x + 5y = 1, x – 3y = 6 and x + 5y + 2 = 0 are concurrent
They will pass through the same point
Now 2x + 5y = 1 …..(i)
x – 3y = 6 ……(ii)
Multiply (i) by 3 and (ii) by 5, we get :
-6x + 15y = 3
5x – 15y = 30
Adding we get :
11x = 33 ⇒ x = 3
from (ii),
x – 3y = 6
⇒ 3 – 3y = 6
⇒ -3y = 6 – 3 = 3
⇒ y = -1
Point of intersection of first two lines is (3, -1)
Substituting the values in third line x + 5y + 2 = 0
L.H.S. = x + 5y + 2 = 3 + 5(-1) + 2 = 3 – 5 + 2 = 5 – 5 = 0 = R.H.S.
Hence the given three lines are concurrent.

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.