Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity (With Applications to Maps and Models) Ex 15A
These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15A.
Other Exercises
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15A
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15B
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15C
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15D
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15E
Question 1.
In the figure, given below, straight lines AB and CD intersect at P; and AC || BD. Prove that:
(i) ΔAPC and ΔBPD are similar.
(ii) If BD = 2.4 cm AC = 3.6 cm, PD = 4.0 cm and PB = 3.2 cm; find the lengths of PA and PC.
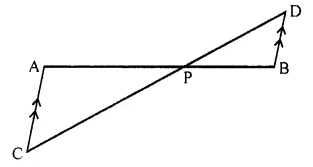
Solution:
Two line segments AB and CD intersect each other at P.
AC || BD To prove:
(i) ΔAPC ~ ΔBPD
(ii) If BD = 2.4cm, AC = 3.6cm, PD = 4.0 cm and PB = 3.2, find length of PA and PC
Proof:
(i) In ΔAPC and ΔAPD
∠APC = ∠BPD (Vertically opp. angles)
∠PAC = ∠PBD (Alternate angles)
ΔAPC ~ ΔBPD (AA axiom)

Question 2.
In a trapezium ABCD, side AB is parallel to side DC; and the diagonals AC and BD intersect each other at point P. Prove that:
(i) ΔAPB is similar to ΔCPD.
(ii) PA x PD = PB x PC.
Solution:
In trapezium ABCD AB || DC
Diagonals AC and BD intersect each other at P.
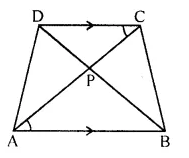
To prove:
(i) ΔAPB ~ ΔCPD.
(ii) PA x PD= PB x PC.
Proof: In ΔAPB and ΔCPD
∠APB = ∠CPD (Vertically opposite angles)
∠PAB = ∠PCD (Alternate angles)
ΔAPB ~ ΔCPD (AA axiom)
\(\frac { PA }{ PC }\) = \(\frac { PB }{ PD }\)
=> PA x PD = PB x PC
Hence proved.
Question 3.
P is a point on side BC of a parallelogram ABCD. If DP produced meets AB produced at point L, prove that:
(i) DP : PL = DC : BL.
(ii) DL : DP = AL : DC.
Solution:
P is a point on side BC of a parallelogram ABCD.
DP is produced to meet AB produced at L.
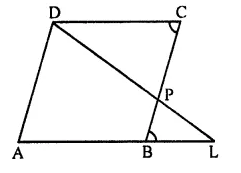
To prove:
(i) DP : PL = DC : BL
(ii) DL : DP = AL : DC.
Proof:
(i) In ΔBPL and ΔCPD
∠BPL = ∠CPD (Vertically opposite angles)
∠PBL = ∠PCD (Alternate angles)
ΔBPL ~ ΔCPD (AA axiom)

Question 4.
In quadrilateral ABCD, the diagonals AC and BD intersect each other at point O. If AO = 2CO and BO = 2DO; show that:
(i) ΔAOB is similar to ΔCOD.
(ii) OA x OD = OB x OC.
Solution:
Given : In quadrilateral ABCD, diagonals AC and BD intersect each other at O.
AO = 2CO, BO = 2DO.
To prove:
(i) ΔAOB is similar to ΔCOD.
(ii) OA x OD = OB x OC.
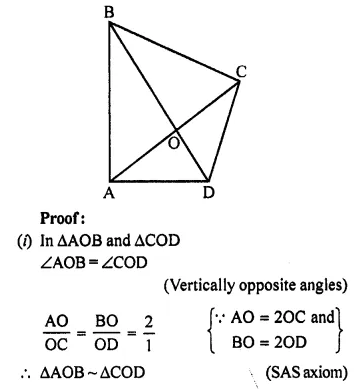

Question 5.
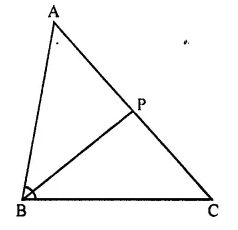
In ΔABC, angle ABC is equal to twice the angle ACB, and bisector of angle ABC meets the opposite side at point P. Show that:
(i) CB : BA = CP : PA
(ii) AB x BC = BP x CA
Solution:
In ΔABC,
∠ABC = 2∠ACB
Bisector of ∠ABC meets AC in P.
To prove:
(i) CB : BA = CP : PA
(ii) AB x BC = BP x CA
Proof:
(i) In ΔABC,
BP is the bisector of ∠ABC

Question 6.
In ΔABC; BM ⊥ AC and CN ⊥ AB; show that:
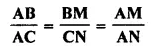
Solution:
In ΔABC,
BM ⊥ AC and CN ⊥ AB
To prove:
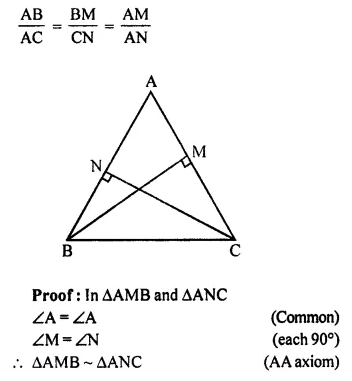

Question 7.
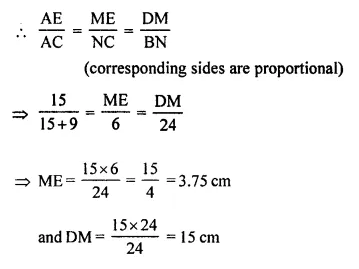
In the given figure, DE // BC, AE = 15 cm, EC = 9 cm, NC = 6 cm and BN = 24 cm.
(i) Write all possible pairs of similar triangles.
(ii) Find lengths of ME and DM.
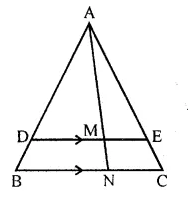
Solution:
In the given figure,
DE || BC
AE = 15 cm, EC = 9 cm NC = 6 cm and BN = 24 cm
(i) Write all the possible pairs of similar triangles.
(ii) Find lengths of ME and DM
Proof:
(i) In ΔABC
DE || BC
Pairs of similar triangles are
(a) ΔADE ~ ΔABC
(b) ΔADM ~ ΔABN
(c) ΔAME ~ ΔANC
(ii) ΔAME ~ ΔANC
and ΔADM ~ ΔABN
Question 8.
In the given figure, AD = AE and AD² = BD x EC
Prove that: triangles ABD and CAE are similar.
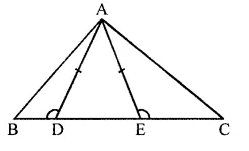
Solution:
In the given figure,
AD = AE
AD² = BD x EC
To prove: ΔABD ~ ΔCAE
Proof: In ΔADC, AD = AE
∠ADE = ∠AED (Angles opposite to equal sides)
But ∠ADE + ∠ADB = ∠AED + ∠AEC = 180°
∠ADB = ∠AEC
AD² = BD x EC
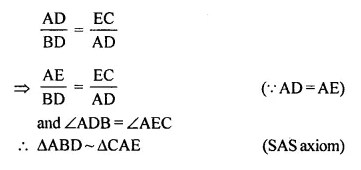
Question 9.
In the given figure, AB // DC, BO = 6 cm and DQ = 8 cm; find: BP x DO.
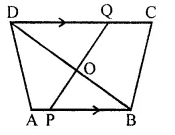
Solution:
In the given figure, AB || DC,
BO = 6 cm, DQ = 8 cm
Find BP x DO
In ΔODQ and ΔOPB
∠DOQ = ∠POB (Vertically opposite angles)
∠DQO = ∠OPB (Alternate angles)
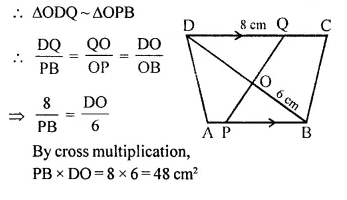
Question 10.
Angle BAC of triangle ABC is obtuse and AB = AC. P is a point in BC such that PC = 12 cm. PQ and PR are perpendiculars to sides AB and AC respectively. If PQ = 15 cm and PR = 9 cm; find the length of PB.
Solution:
In ΔABC, ∠ABC is an obtused angle,
AB =AC
P is a point on BC such that PC = 12 cm
PQ and PR are perpendiculars to the sides AB and AC respectively.
PQ = 15 cm and PR = 9 cm
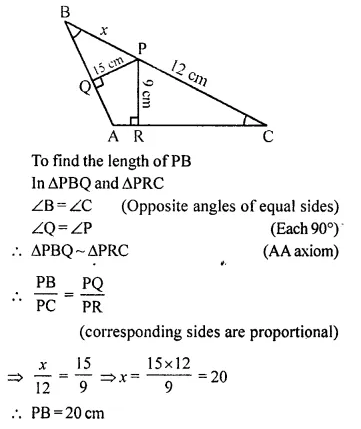
Question 11.
State, true or false :
(i) Two similar polygons are necessarily congruent
(ii) Two congruent polygons are necessarily similar.
(iii) All equiangular triangles are similar.
(iv) All isosceles triangles are similar.
(v) Two isosceles-right triangles are similar.
(vi) Two isosceles triangles are similar, if an angle of one is congruent to the corresponding angle of the other.
(vii) The diagonals of a trapezium, divide each other into proportional segments.
Solution:
(i) False,
(ii) True,
(iii) True,
(iv) False,
(v) True,
(vi) True,
(vii) True.
Question 12.
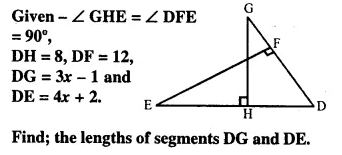
Solution:
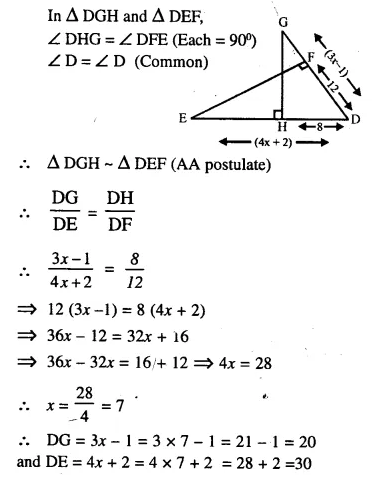
Question 13.
D is a point on the side BC of triangle ABC such that angle ADC is equal to angle BAC. Prove that CA² = CB x CD.
Solution:
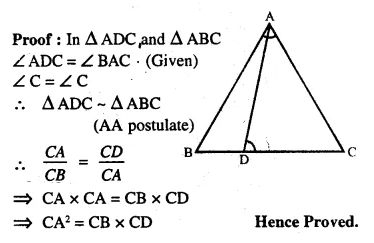
Question 14.
In the given figure, ΔABC and ΔAMP are right angled at B and M respectively.
Given AC = 10 cm, AP = 15 cm and PM = 12 cm.
(i) Prove ΔABC ~ ΔAMP
(ii) Find AB and BC.
Solution:
(i) In ΔABC and ΔAMP,
∠A = ∠A (Common)
∠ABC = ∠AMP (Each = 90°)
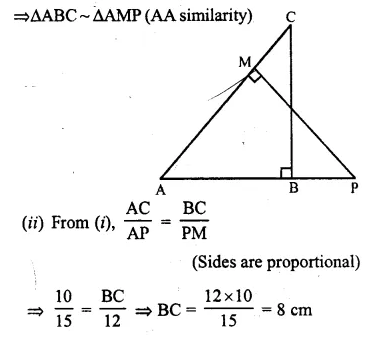
From right triangle ABC, we have
AC² = AB² + BC² (Pythagoras Theorem)
⇒ 10² = AB² + 8²
⇒ 100 = AB² + 64
⇒ AB² = 100 – 64 = 36
⇒ AB = 6 cm
Hence, AB = 6 cm, BC = 8 cm
Question 15.
Given : RS and PT are altitudes of ΔPQR prove that:
(i) ΔPQT ~ ΔQRS,
(ii) PQ x QS = RQ x QT.
Solution:
Proof: In ΔPQT and ΔQRS,
∠PTQ = ∠RSQ (Each = 90°)
∠Q = ∠Q (Common)
ΔPQT ~ ΔQRS (AA postulate)
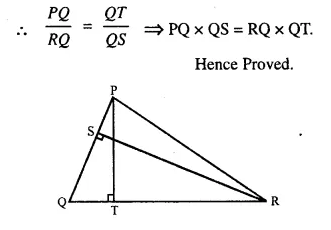
Question 16.
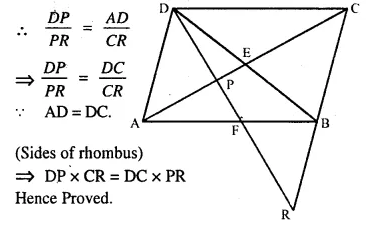
Given : ABCD is a rhombus, DPR and CBR are straight lines.
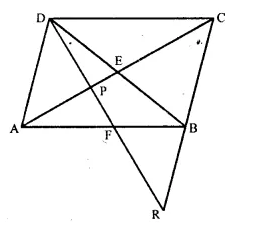
Prove that: DP x CR = DC x PR.
Solution:
Proof: In ΔAPD and ΔPRC
∠DPA = ∠CPR (Vertically opposite angles)
∠PAD = ∠PCR (Alternate angles)
ΔAPD ~ ΔPRC (AA Postulate)
Question 17.
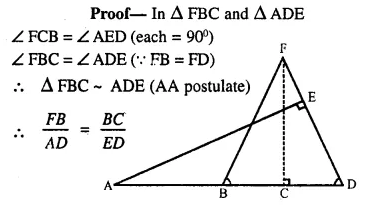
Given: FB = FD, AE ⊥ FD and FC ⊥ AD.
Prove : \(\frac { FB }{ AD }\) = \(\frac { BC }{ ED }\)
Solution:
Question 18.
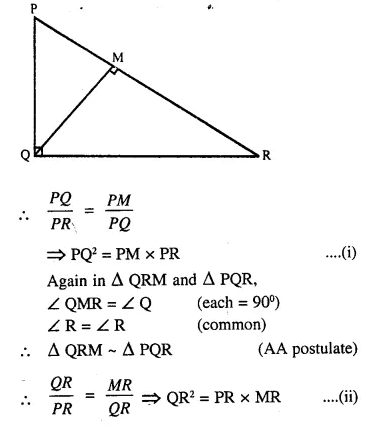
In ΔPQR, ∠Q = 90° and QM is perpendicular to PR, Prove that:
(i) PQ² = PM x PR
(ii) QR² = PR x MR
(iii) PQ² + QR² = PR²
Solution:
Given: In ΔPQR, ∠Q =90°
QM ⊥ PR.
To Prove:
(i) PQ2 = PM x PR
(ii) QR2 = PR x MR
(iii) PQ2 + QR2 = PR2
Proof: In ΔPQM and ΔPQR,
∠QMP = ∠PQR (each = 90°)
∠P = ∠P (Common)
ΔPQM ~ ΔPQR (AA postulate)
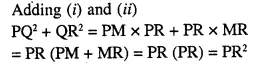
Question 19.
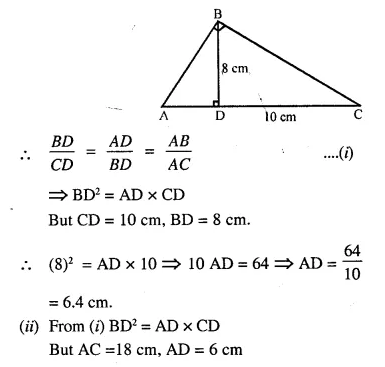
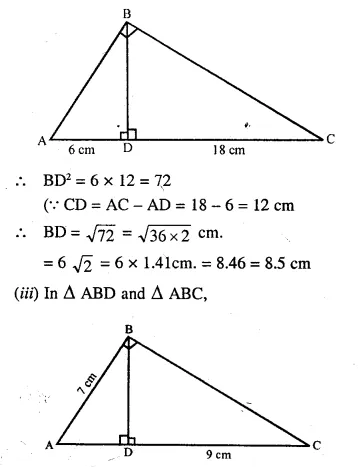
In ΔABC, ∠B = 90° and BD x AC.
(i) If CD = 10 cm and BD = 8 cm; find AD.
(ii) If AC = 18 cm and AD = 6 cm; find BD.
(iii) If AC = 9 cm, AB = 7 cm; find AD.
Solution:
In ΔABC, ∠B = 90°
∠A + ∠C = 90° …….(i)
and in ΔBDC, ∠D = 90°
∠CBD + ∠C = 90° ….(ii)
From (i) and (ii)
∠A + ∠C = ∠CBD + ∠C
∠A = ∠CBD
Similarly ∠C = ∠ABD
Now in ΔABD and ΔCBD,
∠A = ∠CBD and ∠ABD = ∠C
ΔABD ~ ΔCBD (AA Postulate)

Question 20.
In the figure, PQRS is a parallelogram with PQ = 16 cm and QR = 10 cm. L is a point on PR such that RL : LP = 2 : 3. QL produced meets RS at M and PS produced at N.
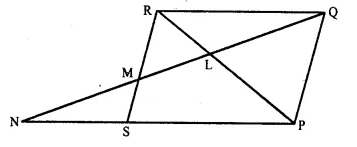
Find the lengths of PN and RM. [1997]
Solution:
In ΔLNP and ΔRLQ
∠LNP = ∠LQR (Alternate angles)
∠NLP = ∠QLR (Vertically opposite angles)
ΔLNP ~ ΔRLQ (AA Postulate)

Question 21.
In quadrilateral ABCD, diagonals AC and BD intersect at point E. Such that AE : EC = BE : ED. Show that ABCD is a parallelogram.
Solution:
Given : In quadrilateral ABCD, diagonals AC and BD intersect each other at E and
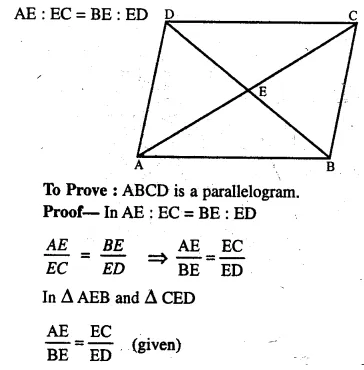
∠AEB = ∠CED (Vertically opposite angles)
ΔAEB ~ ΔCED (SAS axiom)
∠EAB = ∠ECB
∠EBA = ∠CDE
But, these are pairs of alternate angles
AB || CD …..(i)
Similarly we can prove that
AD || BC …..(ii)
from (i) and (ii)
ABCD is a parallelogram.
Question 22.
In ΔABC, AD is perpendicular to side BC and AD² = BD x DC. Show that angle BAC = 90°
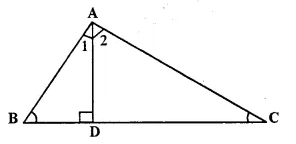
Solution:
Given: In ΔABC, AD x BC and AD² = BD x DC
To Prove: ∠BAC = 90°
Proof:
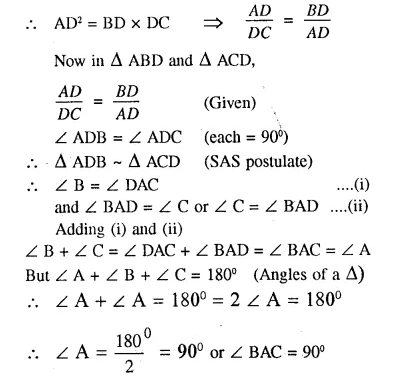
Question 23.
In the given figure AB || EF || DC; AB = 67.5 cm. DC = 40.5 cm and AE = 52.5 cm.
(i) Name the three pairs of similar triangles.
(ii) Find the lengths of EC and EF.
Solution:
(i) In the figure AB || EF || DC
There are three pairs of similar triangles.
(i) ΔAEB ~ ΔDEC
(ii) ΔABC ~ ΔEEC
(iii) ΔBCD ~ ΔEBF
(ii) ΔAEB ~ ΔDEC

Question 24.
In the given figure, QR is parallel to AB and DR is parallel to QB.
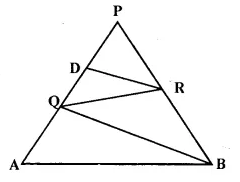
Prove that PQ² = PD x PA.
Solution:
Given: In the figure QR || AB mid DR || QB.
To Prove: PQ² = PD x PA
Proof— In ΔPQB,
DR || QB (given)
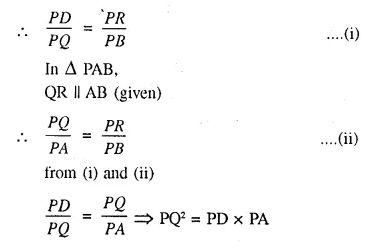
Question 25.
Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn intersecting diagonal AC in L and AD produced in E.
Prove that : EL = 2 BL.
Solution:
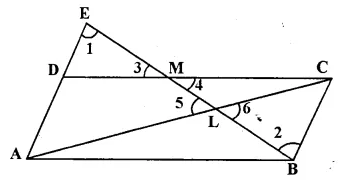
Given: In ||gm. ABCD, M is the mid-point A of CD.
AC is the diagonal.
BM is joined and produced meeting AD produced in E and, intersecting AC in L.
To Prove: EL = 2 BL.
Proof: In ΔEDM, and ΔMBC,
DM = MC (M is mid-point of DC)
∠EMD = ∠CMD (vertically opposite angles)
∠EDM = ∠MCB (Alternate angles)
ΔEDM = ΔMBC (ASA postulate of congruency)
ED = CB = AD (c. p. c. t.)
EA = 2 AD = 2 BC
AB = BC (opposite sides of II gm)
∠DEM = ∠MBC (c. p. c. t.)
Now in ΔELA and ΔBLC,
∠ELA = ∠BLC (vertically opposite angles)
∠DEM or ∠AEL = ∠LBC (proved)
ΔELA ~ ΔBLC (AA postulate)
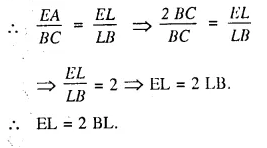
Question 26.
In the figure given below P is a point on AB such that AP : PB = 4 : 3. PQ is parallel to AC.
(i) Calculate the ratio PQ : AC, giving reason for your answer.
(ii) In triangle ARC, ∠ARC = 90° and in triangle PQS, ∠PSQ = 90°.
Given QS = 6 cm, calculate the length of AR. [1999]
Solution:
Given: In ΔABC, P is a point on AB such that AP : PB = 4 : 3
and PQ || AC is drawn meeting BC in Q.
CP is joined and QS ⊥ CP and AR ⊥ CP
To Find:
(i) Calculate the ratio between PQ : AC giving reason.
(ii) In ΔARC ∠ARC= 90°
and In ΔPQS, ∠PSQ = 90°, if QS = 6 cm, calculate AR.
proof:
(i) In ΔABC, PQ || AC.
Question 27.
In the right angled triangle QPR, PM is an altitude.
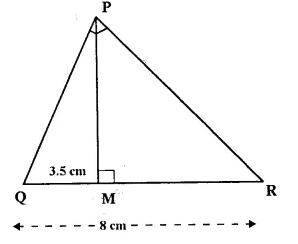
Given that QR = 8 cm and MQ = 3.5 cm. Calculate, the value of PR.
Given: In right angled ΔQPR, ∠P = 90° PM ⊥ QR, QR = 8 cm, MQ = 3.5 cm. Calculate PR [2000]
Solution:
In ΔPQM and ΔQPR,
∠PMQ = ∠QPR (each = 90°)
∠Q = ∠Q (common)
ΔPQM ~ ΔQPR (AA postulate)

Question 28.
In the figure given below, the medians BD and CE of a triangle ABC meet at G.
Prove that
(i) ΔEGD ~ ΔCGB
(ii) BG = 2 GD from (i) above.
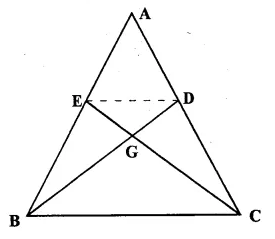
Solution:
Given: In ΔABC, BD and CE are the medians of sides AC and AB respectively which intersect each at G.
To Prove:
(i) ΔEGD ~ ΔCGB
(ii) BG = 2 GD.
Proof: D and E are the mid points of AC and AB respectively.

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15A are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.