Selina Concise Mathematics Class 10 ICSE Solutions Chapter 22 Heights and Distances Ex 22A
These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 22 Heights and Distances Ex 22A
Other Exercises
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 22 Heights and Distances Ex 22A
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 22 Heights and Distances Ex 22B
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 22 Heights and Distances Ex 22C
Question 1.
The height of a tree is \(\sqrt { 3 }\) times the length of its shadow. Find the angle of elevation of the sun.
Solution:
Let AB be the tree and BC be its shadow.

∴ θ = 60°
∵ Angle of elevation of the sun = 60°
Question 2.
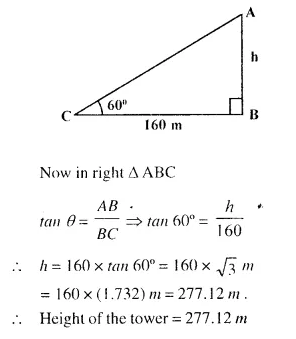
The angle of elevation of the top of a tower, from a point on the ground and at a distance of 160 m from its foot, is found to be 60°. Find the height of the tower.
Solution:
Let AB be the tower and C is the point which is 160 m away from the foot of the tower,
i.e. CB = 160 m
Let height of the tower be x
Question 3.
A ladder is placed along a wall such that its upper end is resting against a vertical wall. The foot of the ladder is 2.4 m from the wall and the ladder is making an angle of 68“ with the ground. Find the height, upto which the ladder reaches.
Solution:
Let AB be the wall and
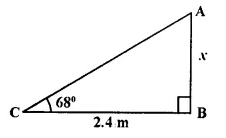
AC be the ladder, which is placed against the wall. If foot is 2.4 m away from the wall i.e. CB = 2.4m1.
Let AB =x m.
In right ∆ ABC,
tan θ = \(\frac { AB }{ BC }\) ⇒ tan 68° = \(\frac { X }{ 2.4 }\)
∴ x = 2.4 x tan 68° = 2.4 x 2.4751
= 5.94 m
Question 4.
Two persons are standing on the opposite sides of a tower. They observe the angles of elevation of the top of the tower to be 30° and 38° respectively. Find the distance between them, if the height of the tower is 50 m.
Solution:
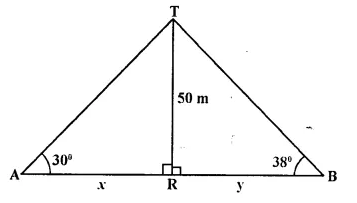
Two persons A and B are standing on the opposite side of the tower TR and height of tower TR = 50 m and angles of elevation with A and B are 30° and 38° respectively. Let AR = x and RB = y
Now in right ∆TAR,

Question 5.
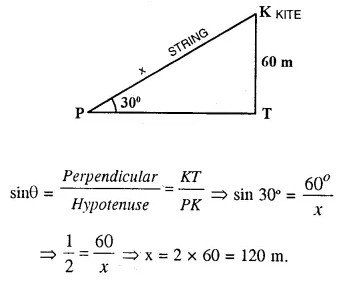
A kite is attached to a string. Find the length of the string, when the height of the kite is 60 m. and the string makes an angle 30° with the ground.
Solution:
Let KT be the height of kite and PK is the string which makes an angle of 30° with the ground.
∴ KT = 60 m
Let KP = xm.
Now in right ∆PKT,
Question 6.
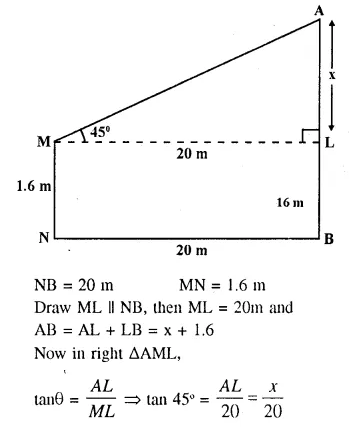
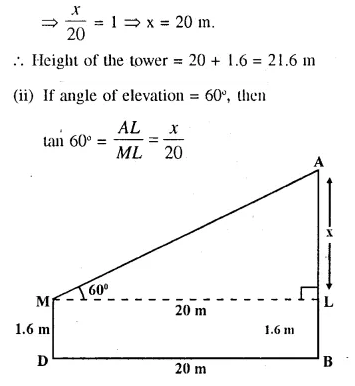
A boy 1.6m tall, is 20 m away from a tower and observes the angle of elevation of the top of the tower to be (i) 45° (ii) 60°. Find the height of the tower in each case.
Solution:
(i) Let AB be the tower and MN be the boy who is 20m away from the foot of the tower.
Let AB = x and angle of elevation = 45°
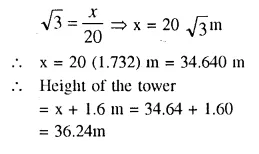
Question 7.
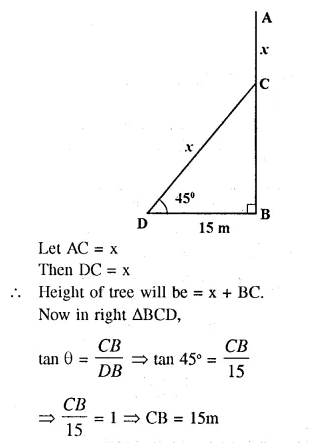
The upper part of a tree, broken over by the wind, makes an angle of 45° with the ground; and the distance from the root to the point where the top of the tree touches the ground, is 15m. What was the height of the tree before it was broken ?
Solution:
Let AB be the tree which was broken at the point C which makes an angle of elevation of 45°, with the ground at a distance of 15m.
BD = 15m
AC = CD
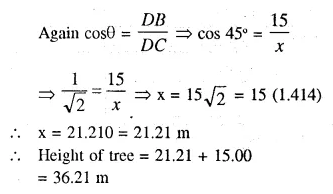
Question 8.
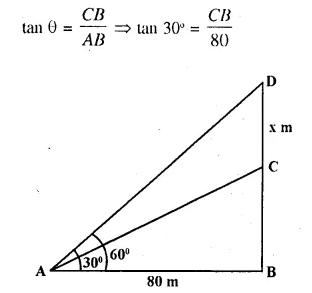
The angle of elevation of the top of an unfinished tower at a point distance 80 m from its base is 30°. How much higher must the tower be raised so that its angle of elevation at the same point may be 60° ?
Solution:
Distance of a point from the tower = 80 m
Angle of elevation = 30°
In second case the elevation of lower = 60°
In first case,

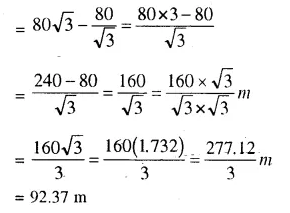
Question 9.
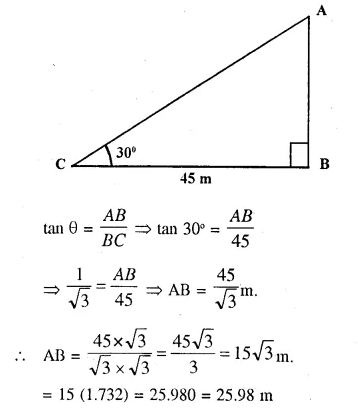
At a particular time, when the sun’s altitude is 30°, the length of the shadow of’C vertical tower is 45 m. Calculate :
(i) height of the tower.
(ii) the length of the shadow of the same tower, when the sun’s altitude is (a) 45° (b) 60°.
Solution:
Shadow of the tower = 45 m and angle of elevation = 30°
Let AB be the lower and BC is its shadow.
∴ CB = 45 m.
Now in right ∆ABC,
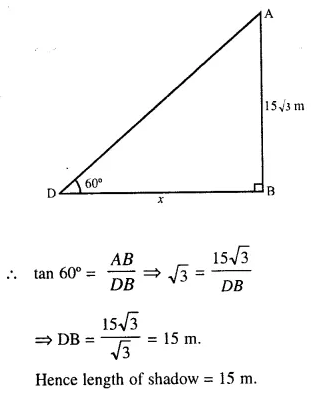
(ii) In second case,
(a) Angle of elevation = 45°
and height of tower = 25.98 m or 15\(\sqrt { 3 }\) m
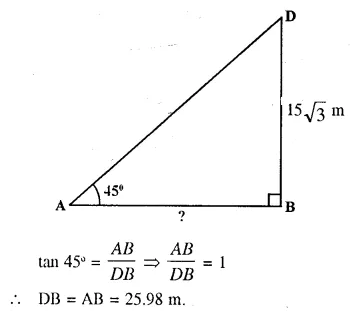
(b) Angle of elevation = 60°
and height of tower = 25.98 m or 15\(\sqrt { 3 }\) m.
Let shadow of the tower DB = xm
Question 10.
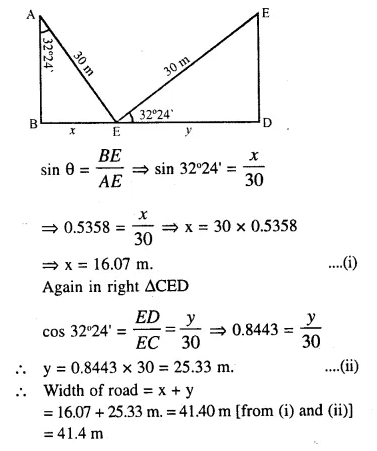
Two vertical poles are on either side of a road. A 30 m long ladder is placed between the two poles. When the ladder rests against one pole, it makes angle 32°24′ with the pole and when it is turned to rest against another pole, it makes angle 32°24′ with the road. Calculate the width of the road.
Solution:
Two poles AB and CD which are at the either end of a road BD. A ladder 30 m long subtends an angle of 32° 24′ with the first pole AB and 32°24′ with the road when it is turned to rest against the second pole CD.
Now in right ∆ABE.
Question 11.
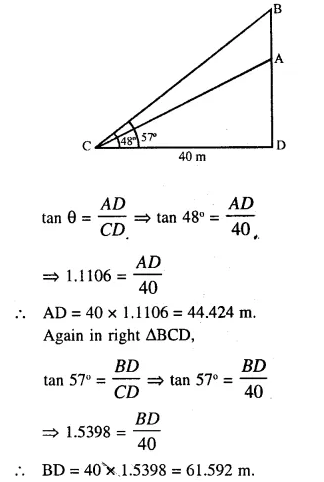
Two climbers are at points A and Bona vertical cliff face. To an observer C, 40 m from the foot of the cliff on the level ground, A is at an elevation of 48° and B of 57°. What is the distance between the climbers ?
Solution:
A and B are two climbers on the cliff and ob-server is at C, 40 m from the foot of the cliff while the angles of elevations of each climber is 48° and 57° respectively.
In right ∆ACD,
![]()
Question 12.
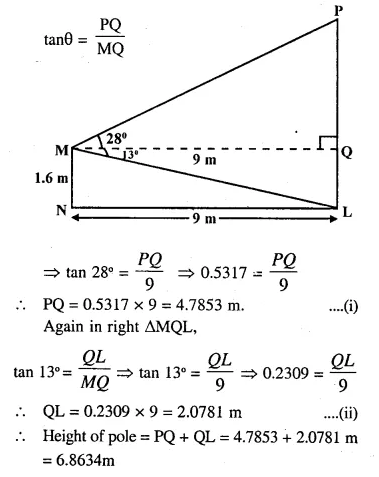
A man stands 9m away from a flag-pole. He observes that angle of elevation of the top of the pole is 28° and the angle of depression of the bottom of the pole is 13°. Calculate the height of the pole.
Solution:
Let PL is the pole and MN is the man The angle of elevation of the top of the pole = 28°
arid the angle of depression of the bottom of the pole =13°
Man is 9 m away from the pole,
i.e. MQ = 9 m
Now in right ∆PMQ,
Question 13.
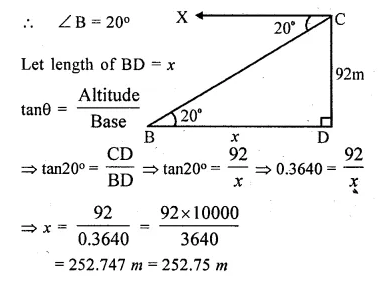
From the top of a cliff 92 m high, the angle of depression of a buoy is 20°. Calculate to the nearest metre the distance of the buoy from the foot of the cliff.
Solution:
Let CD be the cliff and CD = 92m, B is the buoy,
then from C ,
the angle of depression is 20°
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 22 Heights and Distances Ex 22A are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.