Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5D
These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5D.
Other Exercises
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5A
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5B
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5C
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5D
Solve each of the following equations :
Question 1.
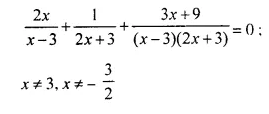
Solution:
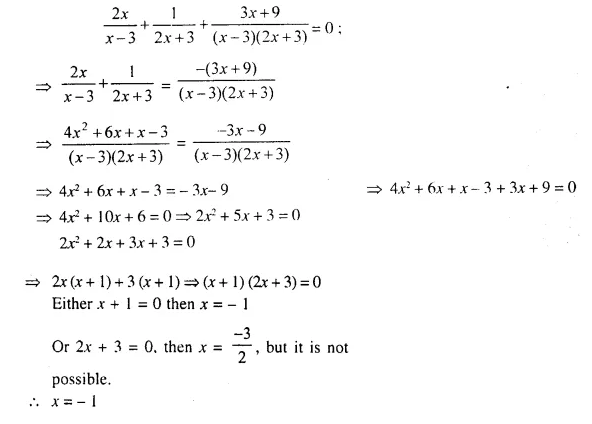
Question 2.
(2x + 3)² = 81
Solution:
(2x + 3)2 = 81
⇒ 4x² + 12x + 9 = 81
⇒ 4x² + 12x + 9 – 81 = 0
⇒ 4x² + 12x – 72 = 0
⇒ x² + 3x – 18 = 0 (Dividing by 4)
⇒ x² + 6x – 3x – 18 = 0
⇒ x (x + 6) – 3 (x + 6) = 0
⇒ (x + 6) (x – 3) = 0
Either x + 6 = 0, then x = -6
or x – 3 = 0, then x = 3
x = 3, – 6
Question 3.
a² x² – b² = 0
Solution:
a² x² – b² = 0
⇒ (ax)² – (b)² =0
⇒ (ax + b) (ax – b) =
Either ax + b = 0, then x = \(\frac { -b }{ a }\)
or ax – b = 0. then x = \(\frac { b }{ a }\)
x = \(\frac { b }{ a }\) , \(\frac { -b }{ a }\)
Question 4.
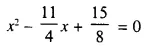
Solution:
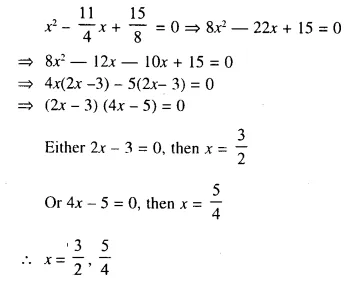
Question 5.
x + \(\frac { 4 }{ x }\) = – 4; x ≠ 0
Solution:
x + \(\frac { 4 }{ x }\) = -4
⇒ x² + 4 = -4x
⇒ x² + 4x + 4 = 0
⇒ (x + 2)² = 0
⇒ x + 2 = 0
⇒ x = – 2
Question 6.
2x4 – 5x² + 3 = 0
Solution:
2x4 – 5x² + 3 = 0
⇒ 2(x²)² – 5x² + 3 = 0
⇒ 2(x²)² – 3x² – 2x² + 3 = 0
⇒ 2x4 – 3x² – 2x² + 3 = 0
⇒ x² (2x² – 3) – 1 (2x² – 3) = 0
⇒ (2x² – 3) (x² – 1) = 0
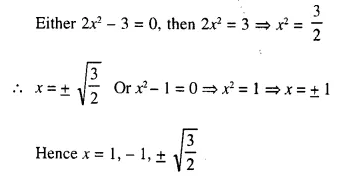
Question 7.
x4 – 2x² – 3 = 0
Solution:
x4 – 2x² – 3 = 0
⇒ (x²)² – 2x² – 3 = 0
⇒ (x²)² – 3x² + x² – 3 = 0
⇒ x² (x² – 3) + 1 (x² -3) = 0
⇒ (x² – 3) (x² + 1) = 0
Either x² – 3 = 0, then x² = 3 ⇒ x = √3
or x² + 1 = 0, then x² = – 1 In this case roots are not real
x = ±√3 or √3 , – √3
Question 8.
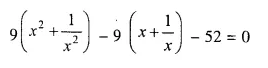
Solution:
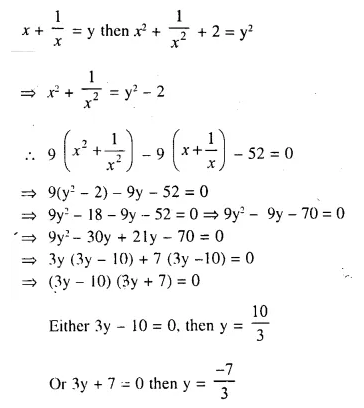
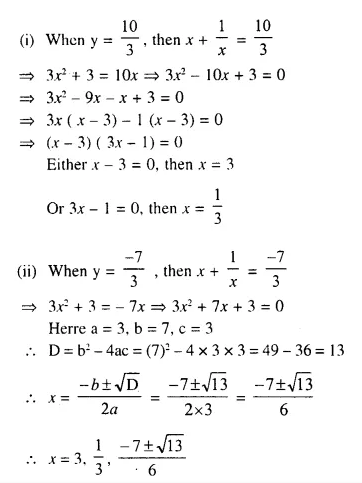
Question 9.
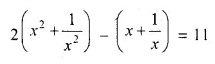
Solution:
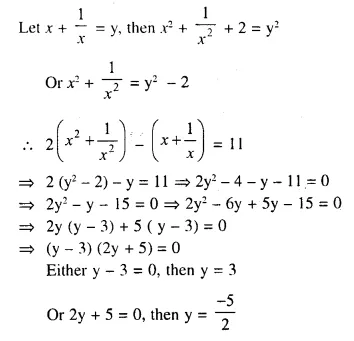
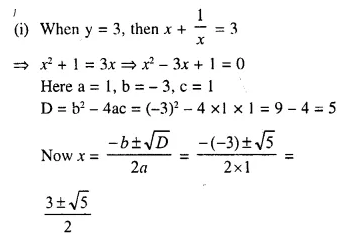
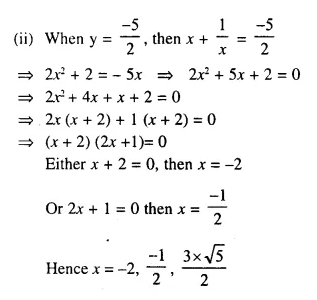
Question 10.
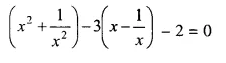
Solution:
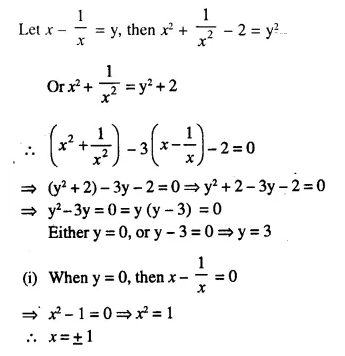
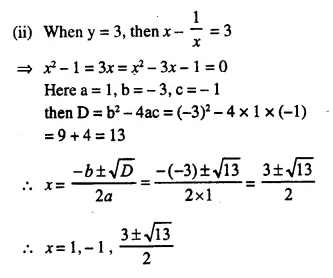
Question 11.
(x² + 5x + 4)(x² + 5x + 6) = 120
Solution:
Let x² + 5x + 4 = y then x² + 5x + 6 = y + 2
Now (x² + 5x + 4) (x² + 5x + 6) = 120
⇒ y (y + 2) – 120 = 0
⇒ y² + 2y – 120 = 0
⇒ y² + 12y – 10y – 120 = 0
⇒ y (y + 12) – 10 (y + 12) = 0
⇒ (y + 12) (y – 10) = 0
Either y + 12 = 0, then y = – 12
or y – 10 = 0, then y = 10
(i) when y = -12, then x² + 5x + 4 = -12
⇒ x² + 5x + 4 + 12 = 0
⇒ x² + 5x + 16 = 0
Here a = 1, b = 5, c = 16
D = b² – 4ac = (5)² – 4 x 1 x 16 = 25 – 64 = -39
D < 0, then roots are not real
(ii) When y = 10, then x² + 5x + 4 = 10
⇒ x² + 5x + 4 – 10 = 0
⇒ x² + 5x – 6 = 0
⇒ x² + 6x – x – 6 = 0
⇒ x (x + 6) – 1 (x + 6) = 0
⇒ (x + 6) (x – 1) = 0
Either x + 6 = 0, then x = – 6
or x – 1 = 0, then x = 1
x = 1, -6
Question 12.
Solve each of the following equations, giving answer upto two decimal places:
(i) x² – 5x – 10 = 0 [2005]
(ii) 3x² – x – 7 = 0 [2004]
Solution:
(i) Given Equation is : x² – 5x – 10 = 0
On comparing with, ax² + bx + c = 0
a = 1, b = -5 , c = -10
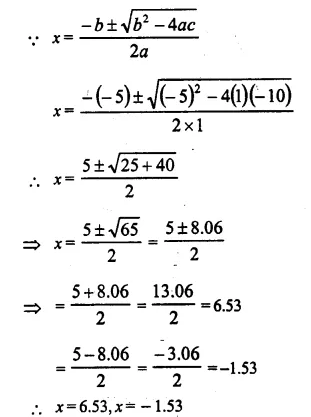
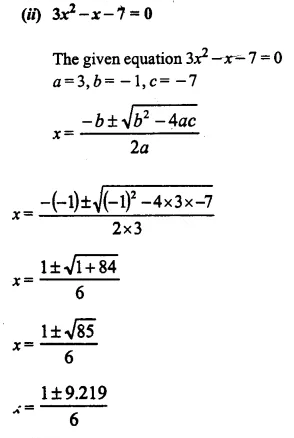
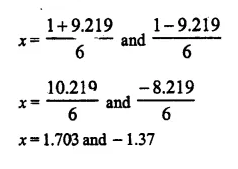
Question 13.
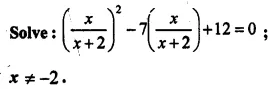
Solution:
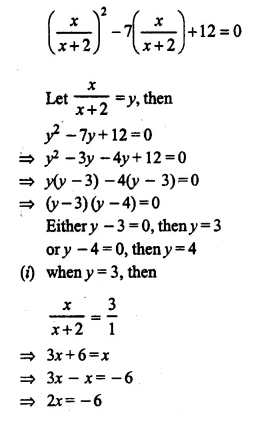
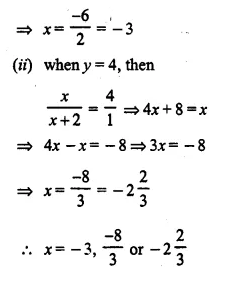
Question 14.
Solve:
(i) x² – 11x – 12 = 0; when x ∈ N
(ii) x² – 4x – 12 = 0; when x ∈ I
(iii) 2x² – 9x + 10 = 0; when x ∈ Q.
Solution:
(i) x² – 11x – 12 = 0
⇒ x² – 12x + x – 12 = 0
⇒ x (x – 12) + 1 (x – 12) = 0
⇒ (x – 12) (x + 1) = 0
Either x – 12 = 0, then x = 12
or x + 1 = 0, then x = -1
x ∈ N
x = 12
(ii) x² – 4x – 12 = 0
⇒ x² – 6x + 2x – 12 = 0
⇒ x (x – 6) + 2 (x – 6)=0
⇒ (x – 6) (x + 2) = 0
Either x – 6 = 0, then x = 6
or x + 2 = 0, then x = -2
x ∈ I
x = 6, -2
(iii) 2x² – 9x + 10 = 0
⇒ 2x² – 4x – 5x + 10 = 0
⇒ 2x (x – 2) – 5 (x – 2) = 0
⇒ (x – 2) (2x – 5) = 0
Either x – 2 = 0, then x = 2
or 2x – 5 = 0, then 2x = 5 ⇒ x = \(\frac { 1 }{ 2 }\)
x ∈ Q
x = 2, \(\frac { 5 }{ 2 }\) or 2, 2.5
Question 15.
Solve: (a + b)² x² – (a + b) x – 6 = 0, a + b ≠ 0.
Solution:
(a + b)² x² – (a + b) x – 6 = 0
Let (a + b) x = y, then y² – y – 6 = 0
⇒ y² – 3y + 2y – 6 = 0
⇒ y (y – 3) + 2 (y – 3) = 0
⇒ (y – 3) (y + 2) = 0
Either y – 3 = 0, then y = 3
or y + 2 = 0, then y = – 2
(i) If y = 3, then
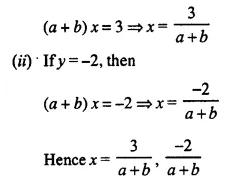
Question 16.
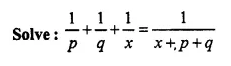
Solution:
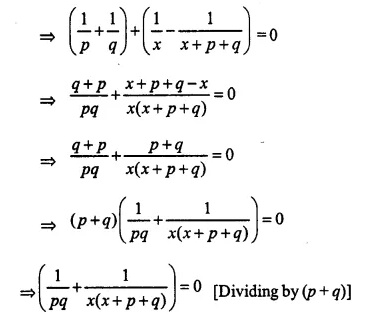
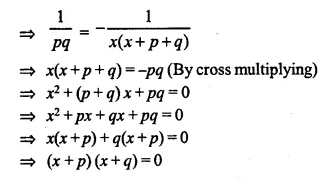
Either x + p = 0, then x = -p
or x + q = 0, then x = -q
Hence x = -p, -q
Question 17.
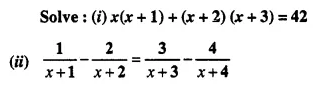
Solution:
(i) x (x + 1) + (x + 2) (x + 3) = 42
⇒ x² + x + x² + 3x + 2x + 6 – 42 = 0
⇒ 2x² + 6x – 36 = 0
⇒ x² + 3x – 18 = 0
⇒ x² + 6x – 3x – 18 = 0
⇒ x (x + 6) – 3(x + 6) = 0
⇒ (x + 6) (x – 3) = 0
Either x + 6 = 0, then x = -6
or x – 3 = 0, then x = 3
Hence x = 3, -6
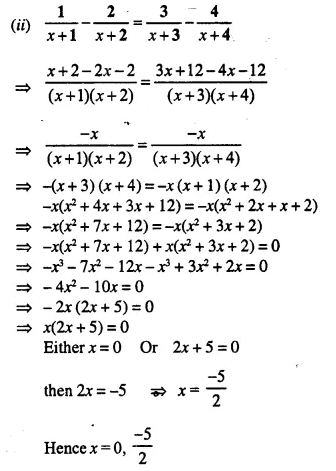
Question 18.
For each equation, given below, find the value of ‘m’ so that the equation has equal roots. Also, find the solution of each equation:
(i) (m – 3) x² – 4x + 1 = 0
(ii) 3x² + 12x + (m + 7) = 0
(iii) x² – (m + 2) x + (m + 5) = 0
Solution:
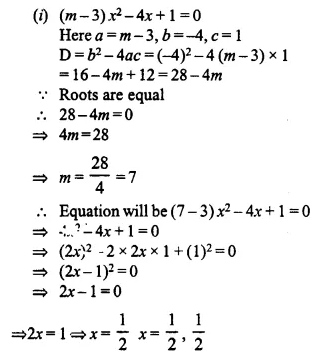
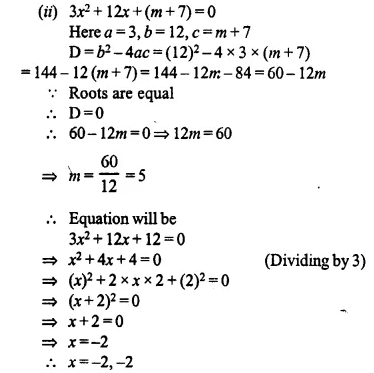
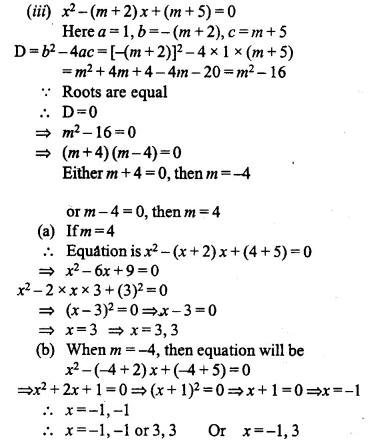
Question 19.
Without solving the following quadratic equation, find the value of ‘p’ for which the roots are equal. px² – 4x + 3 = 0.
Solution:
px² – 4x + 3 = 0 …..(i)
Compare (i) with ax² + bx + c = 0
Here a = p, b = -4, c = 3
D = b² – 4ac = (-4)² – 4.p.(3) = 16 – 12p
As roots are equal, D = 0
16 – 12p = 0
⇒ \(\frac { 16 }{ 12 }\) = p
⇒ p = \(\frac { 4 }{ 3 }\)
Question 20.
Without solving the following quadratic equation, find the value of m for which the given equation has real and equal roots : x² + 2 (m – 1) x + (m + 5) = 0.
Solution:
x² + 2 (m – 1) x + (m + 5) = 0.
Here, a = 1, b = 2 (m – 1), c = m + 5
So, discriminant, D = b² – 4ac
= 4(m – 1)² – 4 x 1 (m + 5)
= 4m² + 4 – 8m – 4m – 20
= 4m² – 12m – 16
For real and equal roots D = 0
So, 4m² – 12m – 16 = 0
⇒ m² – 3m – 4 = 0 (Dividingby4)
⇒ m² – 4m + m – 4 = 0
⇒ m (m – 4) + 1 (m – 4) = 0
⇒ (m – 4) (m + 1) = 0
⇒ m = 4 or m = -1
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 5 Quadratic Equations Ex 5D are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.