Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion (Including Properties and Uses) Ex 7A
These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion Ex 7A.
Other Exercises
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion Ex 7A
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion Ex 7B
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion Ex 7C
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion Ex 7D
Question 1.
If a : b = 5 : 3; find: \(\frac { 5a – 3b }{ 5a + 3b }\)
Solution:
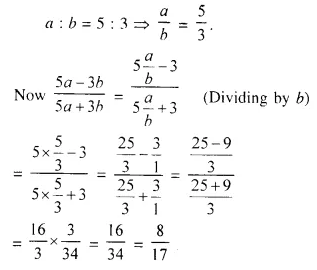
Question 2.
If x : y = 4 : 7; find the value of (3x + 2y) : (5x + y).
Solution:
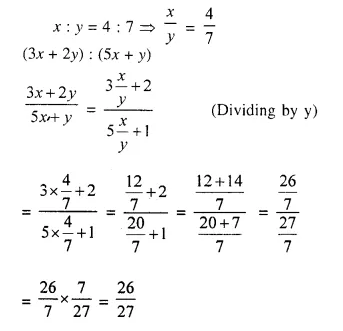
Question 3.
If a : b = 3 : 8, find the value of \(\frac { 4a + 3b }{ 6a – b }\)
Solution:
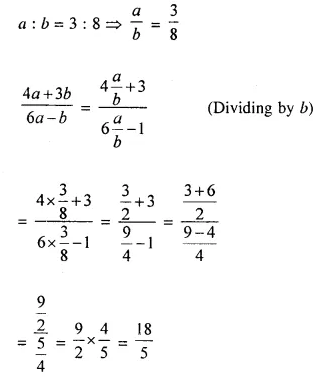
Question 4.
If (a – b): (a + b) = 1 : 11, find the ratio (5a + 4b + 15) : (5a – 4b + 3).
Solution:
(a – b) : (a + b) = 1 : 11
Let a – b = x, then a + b = 11x
Adding we get, 2a = 12x ⇒ a = 6x
Subtracting, -2b = -10x ⇒ b = 5x
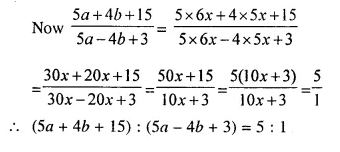
Question 5.
Find the number which bears the same ratio to \(\frac { 7 }{ 33 }\) that \(\frac { 8 }{ 21 }\) does to \(\frac { 4 }{ 9 }\).
Solution:
Let x be the required number, then
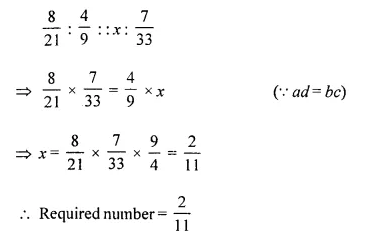
Question 6.
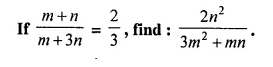
Solution:
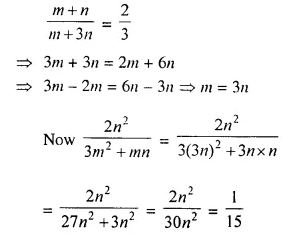
Question 7.
Find \(\frac { x }{ y }\) ; when x² + 6y² = 5xy.
Solution:
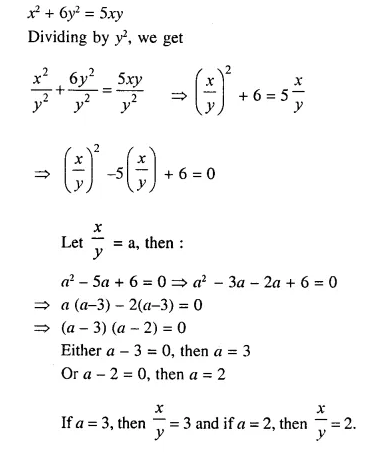
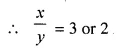
Question 8.
If the ratio between 8 and 11 is the same as the ratio of 2x – y to x + 2y, find the value of \(\frac { 7x }{ 9y }\)
Solution:
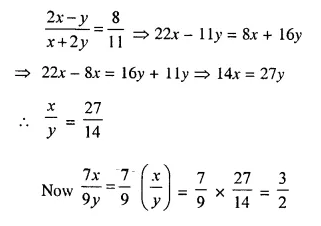
Question 9.
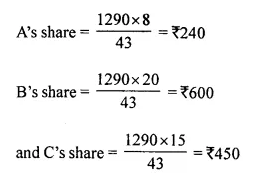
Divide ₹ 290 into A, B and C such that A is \(\frac { 2 }{ 5 }\) of B and B : C = 4 : 3.
Solution:
Total amount = ₹ 1290
A = \(\frac { 2 }{ 5 }\) B and B : C = 4 : 3
⇒ A : B = 2 : 5 and B : C = 4 : 3
LCM of 5, 4 = 20
A : B = 2 x 4 : 5 x 4 = 8 : 20
and B : C = 4 x 5 : 3 x 5 = 20 : 15
A : B : C = 8 : 20 : 15
Sum of ratios = 8 + 20 + 15 = 43
Question 10.
A school has 630 students. The ratio of the number of boys to the number of girls is 3 : 2. This ratio changes to 7 : 5 after the admission of 90 new students. Find the number of newly admitted boys.
Solution:
Number of students = 630
Ratio in boys and girls = 3 : 2
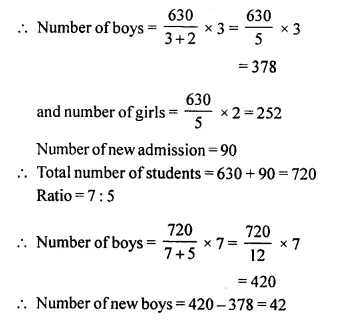
Question 11.
What quantity must be subtracted from each term of the ratio 9 : 17, to make it equal to 1 : 3?
Solution:
Let x be subtracted from each term such that
\(\frac { 9 – x }{ 17 – x }\) = \(\frac { 1 }{ 3 }\)
⇒ 17 – x = 27 – 3x
⇒ -x + 3x = 21 – 17
⇒ 2x = 10
⇒ x = 5
Question 12.
The monthly pocket money of Ravi and Sanjeev are in the ratio 5 : 7. Their expenditures are in the ratio 3 : 5. If each save Rs. 80 every month, find their monthly pocket money. [2012]
Solution:
Let the monthly pocket money of Ravi and Sanjeev be 5x and 7x respectively.
Also, let their expenditure be 3y and 5y respectively. So,
5x – 3y = 80 …(i)
and 7x – 5y = 80 …(ii)
Multiplying (i) by 7 and (ii) by 5 and subtracting, we get
4y = 160 ⇒ y = 40
From (i), 5x = 80 + 3 x 40 = 200 ⇒ x = 40
So, monthly pocket money of Ravi = Rs. 5 x 40 = Rs. 200
and monthly pocket money of Sanjeev = Rs. 7 x 40 = Rs. 280
Question 13.
The work done by (x – 2) men in (4x + 1) days and the work done by (4x + 1) men in (2x – 3) days are in the ratio of 3 : 8. Find the value of x.
Solution:
(x – 2) men can do a work in = (4x +1) days
1 man can do a work in = (4x +1) (x-2) days ….(i)
Again (4x + 1) men can do work in = 2x – 3 days
1 man can do the work in = (2x – 3) (4x + 1) days ….(ii)
From (i) and (ii), we get
(4x + 1) (x – 2) : (2x – 3) (4x + 1) = 3 : 8
⇒ (4x + 1) (x – 2) x 8 = (2x – 3) (4x + 1) x 3
⇒ 8 (4x² – 8x + x – 2) – 3 (8x² + 2x – 12x – 3)
⇒ 32x² – 64x + 8x – 16 = 24x² + 6x – 36x – 9
⇒ 32x² – 64x + 8x – 24x² – 6x + 36x – 16 + 9 = 0
⇒ 8x² – 70x + 44x – 7 = 0
⇒ 8x² – 26x – 7 = 0
⇒ 8x² – 28x + 2x – 7 = 0
⇒ 4x ( 2x – 7) + 1 (2x – 7) = 0
⇒ (2x – 7) (4x + 1) = 0
Either 2x – 7 = 0, then x = \(\frac { 7 }{ 2 }\)
or 4x + 1 = 0, then x = \(\frac { -1 }{ 4 }\) but it is not possible.
x = \(\frac { 7 }{ 2 }\) or 3.5 Ans.
Question 14.
The bus fare between two cities is increased in the ratio 7 : 9. Find the increase in the fare, if :
(i) the original fare is Rs. 245 ;
(ii) the increased fare is Rs. 207.
Solution:
The increase in bus fare between two cities is in the ratio = 7 : 9.
(i) If the original fare is Rs. 245
then increase fare = Rs. 245 x \(\frac { 9 }{ 7 }\) = Rs. 315
Increase = Rs. 315 – Rs. 245 = Rs. 70
(ii) The increased fare is Rs. 207
Original fare = Rs. \(\frac { 207 x 7 }{ 9 }\) = Rs. 161
Increase = Rs. 207 – Rs. 161 = Rs. 46
Question 15.
By increasing the cost of entry ticket to a fair in the ratio 10 : 13; the number of visitors to the fair has decreased in the ratio 6 : 5. In what ratio has the total collection increased or decreased ?
Solution:
Increase in the entry tickets = 10 : 13.
But decrease in visitors = 6 : 5
Let original price of per ticket = Rs. 10
Then increased in price will be = Rs. 13
Collection in first case = Rs. 10 x 6 = Rs. 60
and collection in second case = Rs. 13 x 5 = Rs. 65
Hence increase in collection will be = Rs. 60 : Rs. 65 = 12 : 13
Question 16.
In a basket, the ratio between the number of oranges and the number of apples is 7 : 13. If 8 oranges and 11 apples are eaten, the ratio between the number of oranges and the number of apples becomes 1 : 2. Find the original number of oranges and the original number of apples in the basket.
Solution:
The ratio in number of oranges and apples = 7 : 13
Let number of oranges = 7x
Then number of apples = 13x
When 8 oranges and 11 apples are eaten, then
According to the sum,
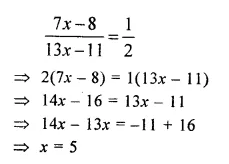
Original number of oranges = 7x = 7 x 5 = 35
and number of apples = 13x = 13 x 5 = 65
Question 17.
In a mixture of 126 kg of milk and water, milk and water are in ratio 5 : 2. How much water must be added to the mixture to make this ratio 3 : 2?
Solution:
Mixture of milk and water = 126 kg
Ratio in milk and water = 5 : 2
Quantity of milk = \(\frac { 126 }{ 5 + 2 }\) x 5
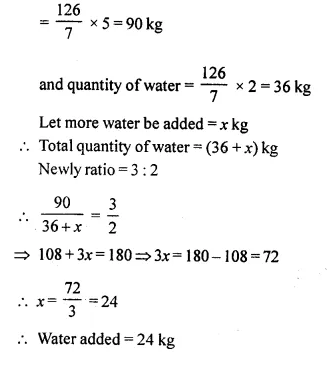
Question 18.
(a) If A : B = 3 : 4 and B : C = 6 : 7, find:
(i) A : B : C
(ii) A : C
(b) If A : B = 2 : 5 and A : C = 3 : 4, find: A : B : C
Solution:
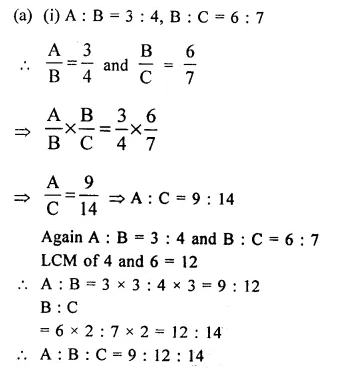
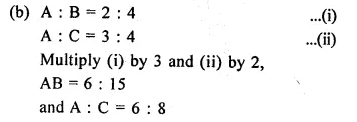
A : B : C = 6 : 15 : 8
Question 19.
(i) If 3A = 4B = 6C ; find A : B : C.
(ii) If 2a = 3b and 4b = 5c, find a : c
Solution:

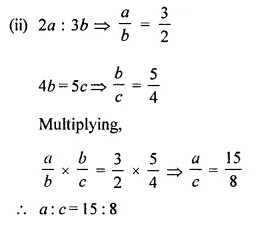
Question 20.
Find the compound ratio of:
(i) 2 : 3, 9 : 14 and 14 : 27.
(ii) 2a : 3b, mn : x² and x : n.
(iii) √2 : 1, 3 : √5 and √20 = 9.
Solution:
(i) Compound ratio of 2 : 3, 9 : 14 and 14 : 27
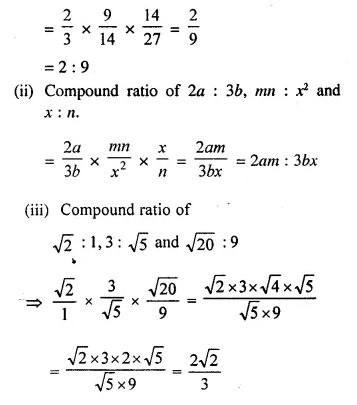
Question 21.
Find the duplicate ratio of:
(i) 3 : 4
(ii) 3√3 : 2√5
Solution:
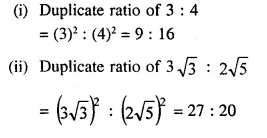
Question 22.
Find triplicate ratio of:
(i) 1 : 3
(ii) \(\frac { m }{ 2 }\) : \(\frac { n }{ 3 }\)
Solution:
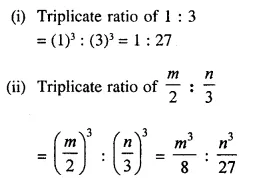
Question 23.
Find sub-duplicate ratio of:
(i) 9 : 16
(ii) (x – y)4 : (x + y)6
Solution:
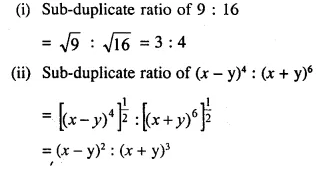
Question 24.
Find sub-triplicate ratio of:
(i) 64 : 27
(ii) x3 : 125y3
Solution:

Question 25.
Find the reciprocal ratio of :
(i) 5 : 8
(ii) \(\frac { x }{ 3 }\) : \(\frac { y }{ 7 }\)
Solution:
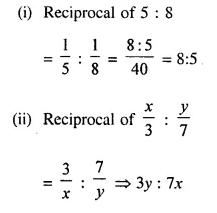
Question 26.
If (x + 3) : (4x + 1) is the duplicate ratio of 3 : 5, find the value of x.
Solution:
(x + 3) : (4x + 1) is the duplicate ratio of 3 : 5
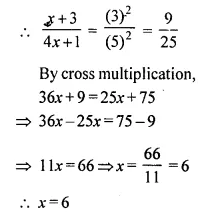
Question 27.
If m : n is the duplicate ratio of m + x : n + x; show that x² = mn.
Solution:

Question 28.
If (3x – 9) : (5x + 4) is the triplicate ratio of 3 : 4, find the value of x.
Solution:
(3x – 9) : (5x + 4) is the triplicate ratio of 3 : 4
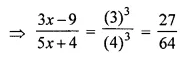
⇒ 27 (5x + 4) = 64 (3x – 9)
⇒ 135x + 108 = 192x – 576
⇒ 192x – 135x = 108 + 576
⇒ 57x = 684
⇒ x = 12
Question 29.
Find the ratio compounded of the reciprocal ratio of 15 : 28, the sub-duplicate ratio of 36 : 49 and the triplicate ratio of 5 : 4.
Solution:
Reciprocal ratio of 15 : 28
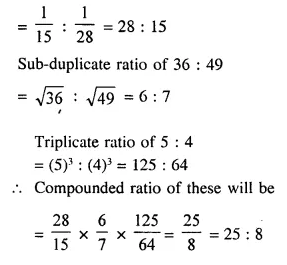
Question 30.
(a) If r² = pq, show that p : q is the duplicate ratio of (p + r) : (q + r).
(b) If (p – x) : (q – x) be the duplicate ratio of p : q then show that : \(\frac { 1 }{ p }\) + \(\frac { 1 }{ q }\) = \(\frac { 1 }{ x }\)
Solution:
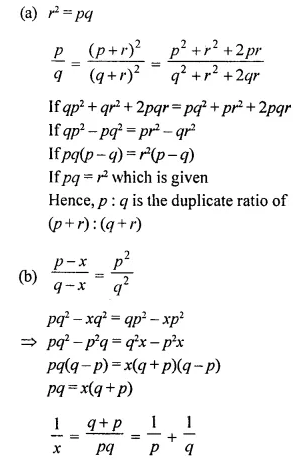
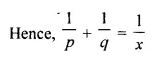
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion Ex 7A are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.