Selina Concise Mathematics Class 10 ICSE Solutions Chapter 8 Remainder and Factor Theorems Ex 8C
These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 8 Remainder and Factor Theorems Ex 8C.
Other Exercises
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 8 Remainder and Factor Theorems Ex 8A
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 8 Remainder and Factor Theorems Ex 8B
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 8 Remainder and Factor Theorems Ex 8C
Question 1.
Show that (x – 1) is a factor of x3 – 7x2 + 14x – 8. Hence, completely factorise the given expression.
Solution:
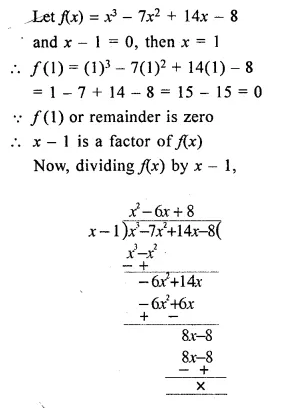
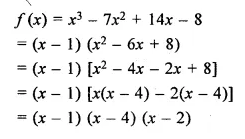
Question 2.
Using Remainder Theorem, factorise : x3 + 10x2 – 37x + 26 completely. (2014)
Solution:
f(x) = x3 + 10x2 – 37x + 26
f(1) = (1)3 + 10(1)2 – 37(1) + 26 = 1 + 10 – 37 + 26 = 0
x = 1
x – 1 is factor of f(x)
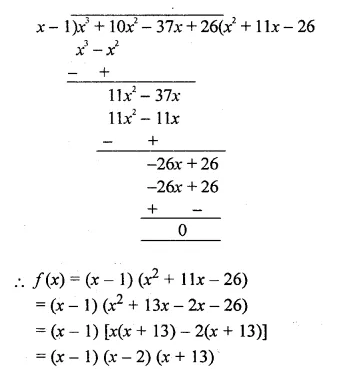
Question 3.
When x3 + 3x2 – mx + 4 is divided by x – 2, the remainder is m + 3. Find the value of m.
Solution:
Let f(x) = x3 + 3x2 – mx + 4
and x – 2 = 0 then x = 2
f(2) = (2)3 + 3(2)2 – m(2) + 4 = 8 + 12 – 2m + 4 = 24 – 2m
Remainder = 24 – 2m
But, remainder is given m + 3
m + 3 = 24 – 2m
⇒ m + 2m = 24 – 3
⇒ 3m = 21
⇒ m = 7
Hence m = 7
Question 4.
What should be subtracted from 3x3 – 8x2 + 4x – 3, so that the resulting expression has x + 2 as a factor ?
Solution:
The number to be subtracted = Remainder obtained by dividing 3x3 – 8x2 + 4x – 3 by x + 2
Let f(x) = 3x3 – 8x2 + 4x – 3
and x + 2 = 0, then x = – 2
Remainder = f(-2) = 3 (-2)3 – 8 (-2)2 + 4 (-2) – 3 = -24 – 32 – 8 – 3 = -67
Hence the number to be subtracted = – 67
Question 5.
If (x + 1) and (x – 2) are factors of x3 + (a + 1) x2 – (b – 2) x – 6, find the values of a and 6. And then, factorise the given expression completely.
Solution:
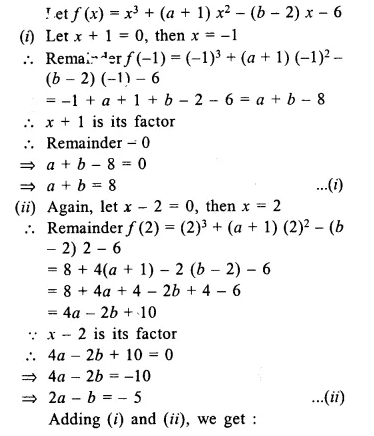
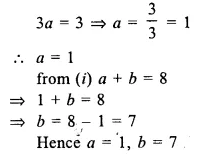
Question 6.
If x – 2 is a factor of x2 – ax + b and a + b = 1, find the values of a and b.
Solution:
(x – 2) is a factor of x2 + ax + b
Let x – 2 = 0 ⇒ x = 2
Now x2 + ax + b = (2)2 + a x 2 + b = 4 + 2a + b = 2a + b + 4
x – 2 is the factor Remainder = 0 or 2a + b + 4 = 0
⇒ 2a + b = -4 …(i)
But a + b = 1 (given) …(ii)
Subtracting, we get : a = -5
Substituting the value of a in (ii)
-5 + b = 1 ⇒ b = 1 + 5 ⇒ b = 6
Hence a = -5, b = 6
Question 7.
Factorise x3 + 6x2 + 11x + 6 completely using factor theorem.
Solution:
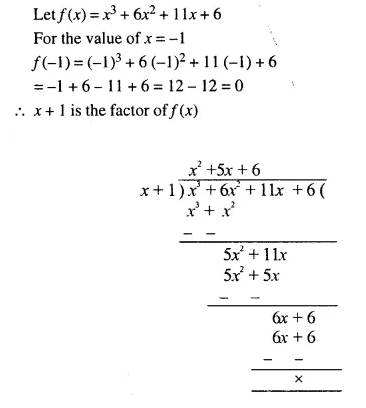
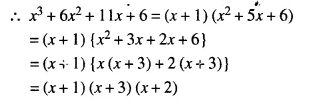
Question 8.
Find the value of ‘m’ if mx3 + 2x2 – 3 and x2 – mx + 4 leave the same remainder when each is divided by x – 2.
Solution:
Let f(x) = mx3 + 2x2 – 3
g (x) = x2 – mx + 4
Let x – 2 = 0, then x = 2
f(2) = m (2)3 + 2 (2)2 – 3 = 8m + 8 – 3 = 8m + 5
g(2) = (2)2 – mx2 + 4 = 4 – 2m + 4 = 8 – 2m
In both cases the remainder is same
8m + 5 = 8 – 2m
⇒ 8m + 2m = 8 – 5
⇒ 10m = 3
⇒ m = \(\frac { 3 }{ 10 }\)
Question 9.
The polynomial px3 + 4x2 – 3x + q is completely divisible by x2 – 1; find the values of p and q. Also, for these values of p and q, factorize the given polynomial completely.
Solution:
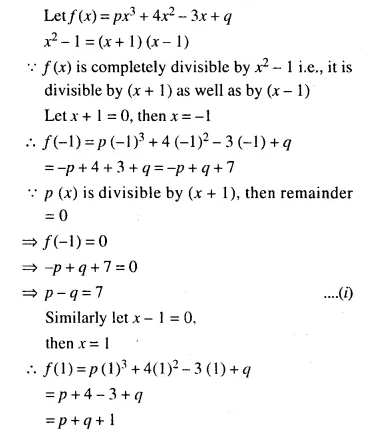
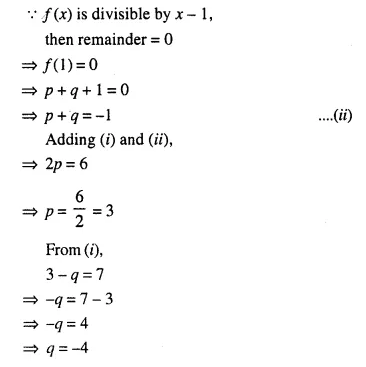
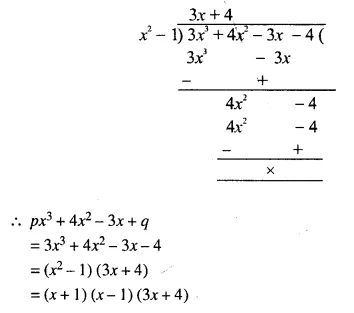
Question 10.
Find the number which should be added to x2 + x + 3 so that the resulting polynomial is completely divisible by (x + 3).
Solution:
Let k be added to f(x), then f(x) = x2 + x + 3 + k
Let x + 3 = 0, then x = -3
f(-3) = (-3)2 + (-3) + 3 + k = 9 – 3 + 3 + k = 9 + k
f(x) is divisible by x + 3, then remainder will be 0.
9 + k = 0 ⇒ k = -9
-9 should be added
Question 11.
When the polynomial x3 + 2x2 – 5ax – 7 is divided by (x – 1), the remainder is A and when the polynomial x3 + ax2 – 12x + 16 is divided by (x + 2), the remainder is B. Find the value of ‘a’ if 2A + B = 0.
Solution:
Let f(x) = x3 + 2x2 – 5ax – 1
and let x – 1 = 0, then x = 1
f(1) = (1)3 + 2(1)2 – 5a x 1 – 7 = 1 + 2 – 5a – 7 = -5a – 4
-5a – 4 = A ….(i)
Let g (x) = x3 + ax2 +12x + 16
and let x + 2 = 0, then x = -2
g (-2) = (-2)3 + a (-2)2 – 12 (-2) + 16 = -8 + 4a + 24 + 16 = 32 + 4a
32 + 4a = B ….(ii)
2A + B = 0
2 (-5a – 4) + 32 + 4a = 0
⇒ -10a – 8 + 32 + 4a = 0
⇒ -6a + 24 = 0
⇒ 6a = 24
⇒ a = 4
a = 4
Question 12.
(3x + 5) is a factor of the polynomial (a – 1) x3 + (a + 1) x2 – (2a + 1) x – 15. Find the value of ‘a’. For this value of ‘a’, factorise the given polynomial completely.
Solution:
Let f(x) = (a – 1) x3 + (a + 1) x2 – (2a + 1) x – 15
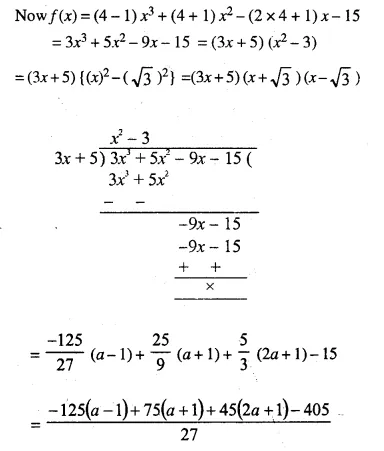
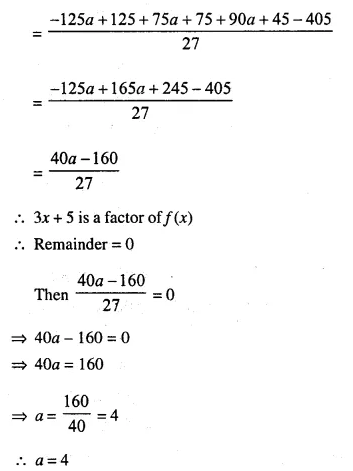
Question 13.
When divided by x – 3 the polynomials x3 – px2 + x + 6 and 2x3 – x2 – (p + 3) x – 6 leave the same remainder. Find the value of ‘p.’
Solution:
When (x – 3) divides x3 – px2 + x + 6,
then Remainder = p(3) = (3)3 – p(3)2 + (3) + 6 = 27 – 9p + 9 = 36 – 9p
When (x – 3) divides 2x3 – x2 – (p + 3) x – 6,
then Remainder = p(3) = 2(3)3 – (3)2 – (p + 3) (3) – 6
= 54 – 9 – 3p – 9 – 6 = 30 – 3p
A.T.Q. both remainders are equal
⇒ 36 – 9p = 30 – 3p
⇒ 36 – 30 = -3p + 9p
⇒ 6 = 6p
⇒ p = 1
Question 14.
Use the Remainder Theorem to factorise the following expression : 2x3 + x2 – 13x + 6
Solution:
(a) By hit and trial, putting x = 2, we have
2 (8) + 4 – 26 + 6 = 0
⇒ (x – 2) is the factor of 2x3 + x2 – 13x + 6
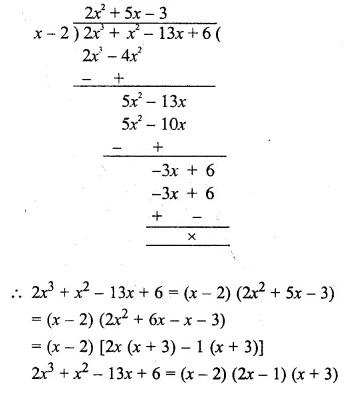
Question 15.
Using remainder theorem, find the value of k if on dividing 2x3 + 3x2 – kx + 5 by x – 2, leaves a remainder 7. (2016)
Solution:
Let f(x) = 2x3 + 3x2 – kx + 5 By the remainder theorem,
f(2) = 7
⇒ 2(2)3 + 3(2)2 – k(2) + 5 = 7
⇒ 2(8) + 3(4) – k(2) + 5 = 7
⇒ 16 + 12 – 2k + 5 = 7
⇒ 2k = 16 + 12 + 5 – 7
⇒ 2k = 26
⇒ k = 13
The value of k is 13.
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 8 Remainder and Factor Theorems Ex 8C are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.