Selina Concise Mathematics Class 10 ICSE Solutions Chapter 9 Matrices Ex 9A
These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 9 Matrices Ex 9A.
Other Exercises
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 9 Matrices Ex 9A
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 9 Matrices Ex 9B
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 9 Matrices Ex 9C
- Selina Concise Mathematics Class 10 ICSE Solutions Chapter 9 Matrices Ex 9D
Question 1.
State, whether the following statements are true or false. If false, give a reason.
(i) If A and B are two matrices of orders 3 x 2 and 2 x 3 respectively; then their sum A + B is possible,
(ii) The matrices A 2 x3, and B 2 x 3, are conformable for subtraction,
(iii) Transpose of a 2 x 1 matrix is a 2 x 1 matrix,
(iv) Transpose of a square matrix is a square matrix,
(v) A column matrix has many columns and only one row.
Solution:
(i) False, because the orders of both the matrices are not same,
(ii) True,
(iii) False, because transpose of a 2 x 1 matrix is a 1 x 2 matrix,
(iv) True,
(v) False, because it has only one column and may have many rows.
Question 2.
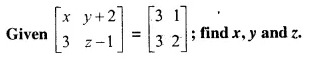
Solution:
Comparing the elements in order, we get that :
x = 3
y + 2 = 1 ⇒ y = 1 – 2 = -1
z – 1 = 2 ⇒ z = 2 + 1 = 3
Hence x = 3, y = -1 , z = 3
Question 3.
Solve for a, b and c; if :
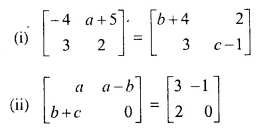
Solution:
(i) Comparing the elements in order, we get
-4 = b + 4 ⇒ – b = 4 + 4 = 8 ⇒ b = – 8
a + 5 = 2 ⇒ a = 2 – 5= -3
2 = c – 1 ⇒ c = 2 + 1 = 3
Hence a = -3, b = -8, c = 3
(ii) Comparing the elements in order, we get
a = 3
a – b = – 1 ⇒ 3 – b = -1 ⇒ -b = -1 – 3 ⇒ -b = -4 ⇒ b = 4
b + c = 2 ⇒ 4 + c = 2 ⇒ c = 2 – 4 = -2
Hence a = 3, b = 4, c = – 2
Question 4.
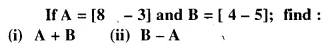
Solution:
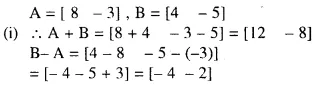
Question 5.
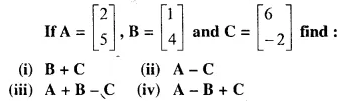
Solution:
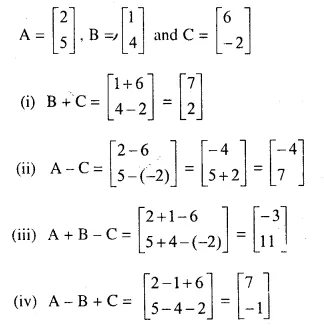
Question 6.
Wherever possible, write each of the following as a single matrix.
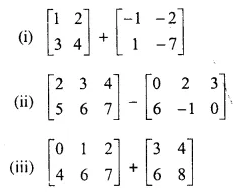
Solution:
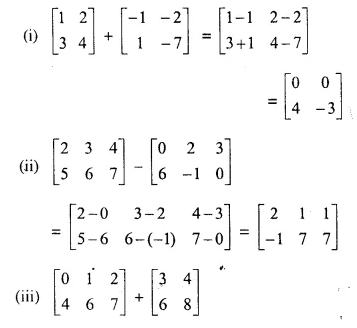
This is not possible because both the matrices are not of the same order.
Question 7.
Find, x and y from the following equations:
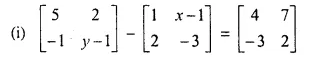
(ii) [-8 x] + [y -2] = [-3 2]
Solution:
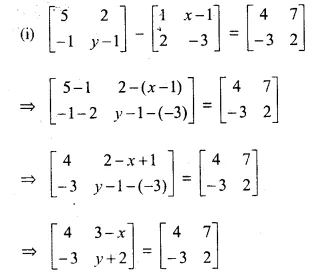
Comparing, the elements of two equal martrices:
3 – x = 7 ⇒ x = -7 + 3 = -4
and y + 2 = 2 ⇒ y = 2 – 2 = 0
Hence x = – 4, y = 0
(ii) [-8 x] + [y -2] = [-3 2]
⇒ [-8 + y x – 2] = [-3 2]
Comparing the elements, we get :
-8 + y = -3 ⇒ y = -3 + 8 = 5
x – 2 = 2 ⇒ x = 2 + 2 = 4
Hence x = 4, y = 5
Question 8.
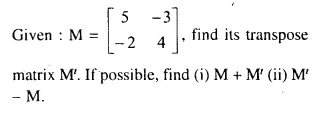
Solution:
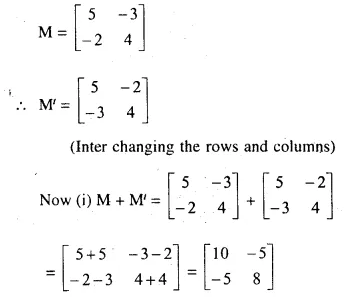
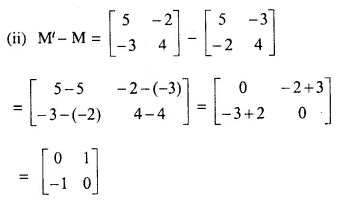
Question 9.
Write the additive inverse of matrices A, B and C
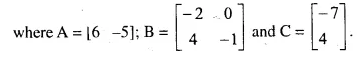
Solution:
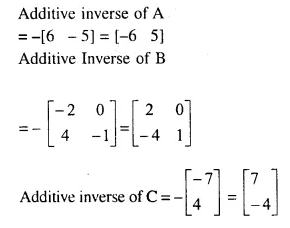
Question 10.
Given A = [ 2 -3], B = [0 2] and C = [-1 4]; find the matrix X in each of the following :
(i) X + B = C – A
(ii) A – X = B + C
Solution:
A = [2 -3], B = [0 2], C = [-1 4]
(i) X + B = C – A
X + [0 2] = [-1 4] – [2 -3]
⇒ X + [0 2] = [- 1 – 2 4 – (-3)]
X + [0 2] = [-3 4 + 3] = [-3 7]
X = [-3 7] – [0 2] = [-3 – 0 7 – 2] = [-3 5]
(ii) A – X = B + C
⇒ -X = B + C – A
⇒ X = A – B – C = [2 -3] – [0 2] – [-1 4] = [2 – 0 – (-1) -3 – 2 – 4] = [ 2 + 1 – 9] = [3 – 9]
Question 11.
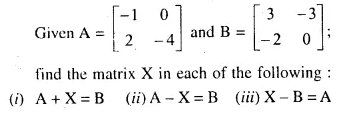
Solution:
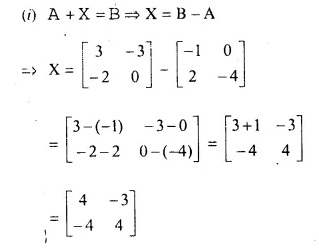
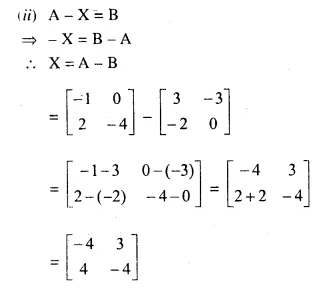
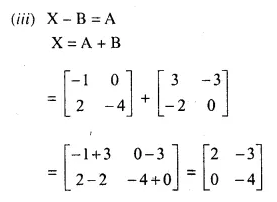
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 9 Matrices Ex 9A are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.