Selina Concise Mathematics Class 8 ICSE Solutions Chapter 17 Special Types of Quadrilaterals

Selina Concise Mathematics Class 8 ICSE Solutions Chapter 17 Special Types of Quadrilaterals

Selina Publishers Concise Mathematics Class 8 ICSE Solutions Chapter 17 Special Types of Quadrilaterals

Special Types of Quadrilaterals Exercise 17 – Selina Concise Mathematics Class 8 ICSE Solutions

Question 1.
In parallelogram ABCD, ∠A = 3 times ∠B. Find all the angles of the parallelogram. In the same parallelogram, if AB = 5x – 7 and CD = 3x +1 ; find the length of CD.
Solution:

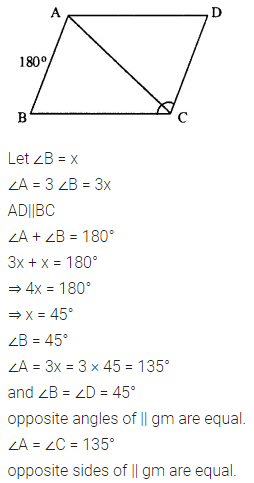
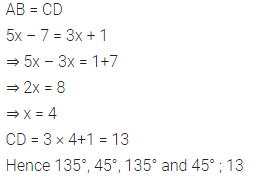
Question 2.
In parallelogram PQRS, ∠Q = (4x – 5)° and ∠S = (3x + 10)°. Calculate : ∠Q and ∠R.
Solution:

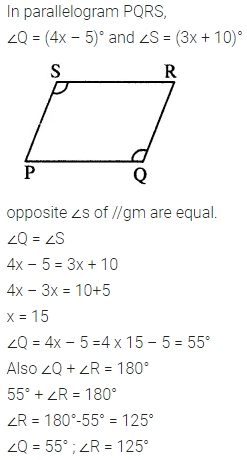
Question 3.
In rhombus ABCD ;
(i) if ∠A = 74° ; find ∠B and ∠C.
(ii) if AD = 7.5 cm ; find BC and CD.
Solution:

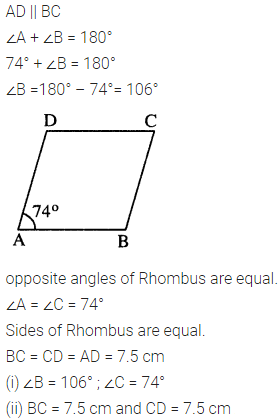
Question 4.
In square PQRS :
(i) if PQ = 3x – 7 and QR = x + 3 ; find PS
(ii) if PR = 5x and QR = 9x – 8. Find QS
Solution:

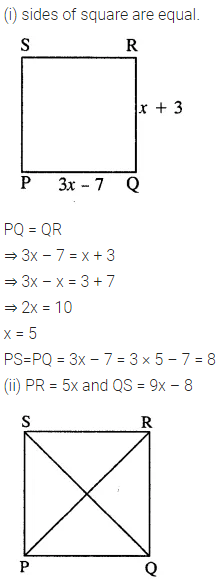
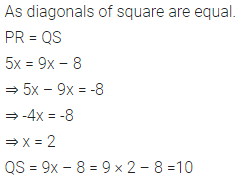
Question 5.
ABCD is a rectangle, if ∠BPC = 124°
Calculate : (i) ∠BAP (ii) ∠ADP

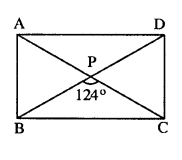
Solution:

Question 6.
ABCD is a rhombus. If ∠BAC = 38°, find :
(i) ∠ACB
(ii) ∠DAC
(iii) ∠ADC.

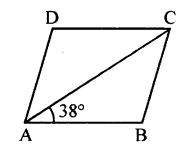
Solution:

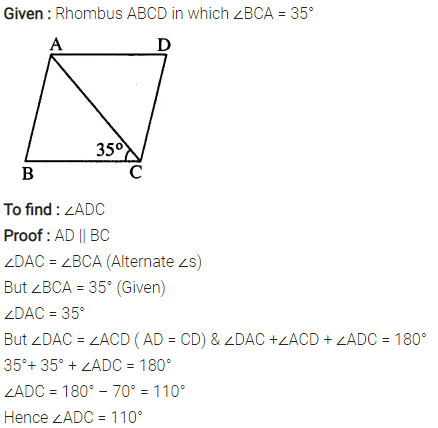
Question 7.
ABCD is a rhombus. If ∠BCA = 35°. find ∠ADC.
Solution:

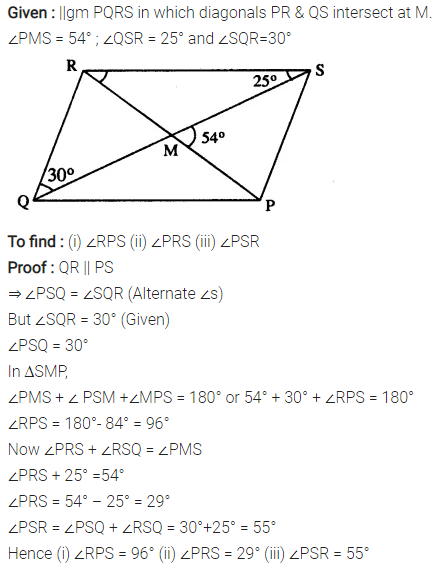
Question 8.
PQRS is a parallelogram whose diagonals intersect at M.
If ∠PMS = 54°, ∠QSR = 25° and ∠SQR = 30° ; find :
(i) ∠RPS
(ii) ∠PRS
(iii) ∠PSR.
Solution:

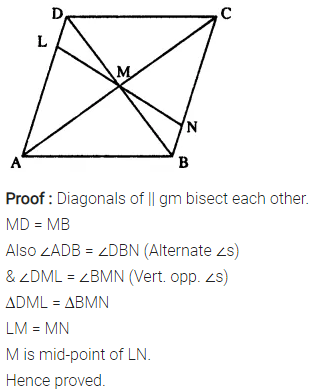
Question 9.
Given : Parallelogram ABCD in which diagonals AC and BD intersect at M.
Prove : M is mid-point of LN.
Solution:

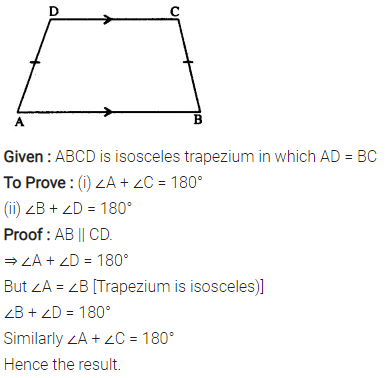
Question 10.
In an Isosceles-trapezium, show that the opposite angles are supplementary.
Solution:

Question 11.
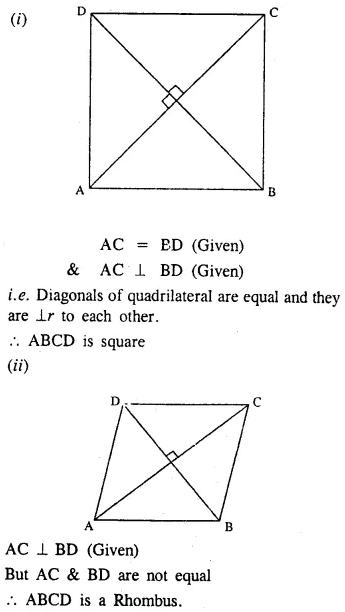
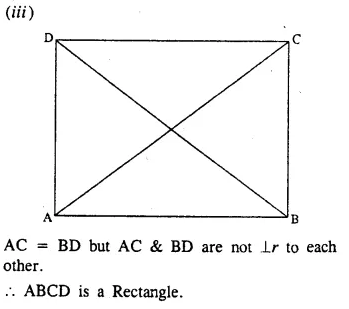
ABCD is a parallelogram. What kind of quadrilateral is it if :
(i) AC = BD and AC is perpendicular to BD?
(ii) AC is perpendicular to BD but is not equal to it?
(iii) AC = BD but AC is not perpendicular to BD?
Solution:

Question 12.
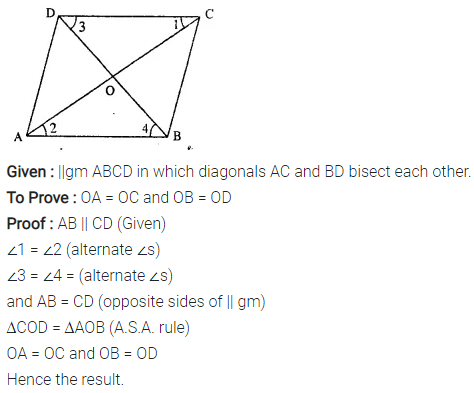
Prove that the diagonals of a parallelogram bisect each other.
Solution:

Question 13.
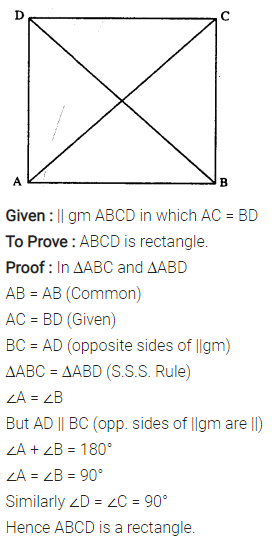
If the diagonals of a parallelogram are of equal lengths, the parallelogram is a rectangle. Prove it.
Solution:

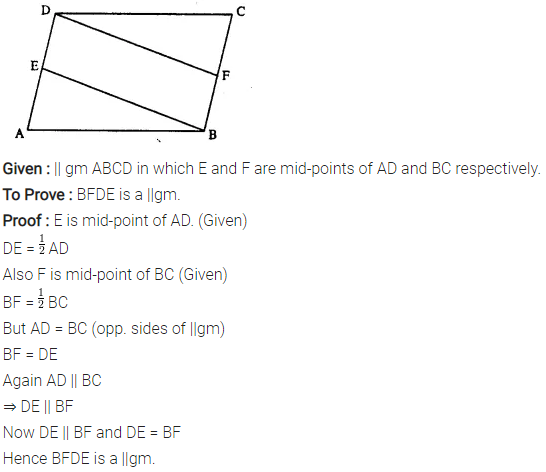
Question 14.
In parallelogram ABCD, E is the mid-point of AD and F is the mid-point of BC. Prove that BFDE is a parallelogram.
Solution:

Question 15.
In parallelogram ABCD, E is the mid-point of side AB and CE bisects angle BCD. Prove that :
(i) AE = AD,
(ii) DE bisects and ∠ADC and
(iii) Angle DEC is a right angle.
Solution:

Question 16.
In the following diagram, the bisectors of interior angles of the parallelogram PQRS enclose a quadrilateral ABCD.

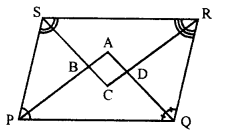
Show that:
(i) ∠PSB + ∠SPB = 90°
(ii) ∠PBS = 90°
(iii) ∠ABC = 90°
(iv) ∠ADC = 90°
(v) ∠A = 90°
(vi) ABCD is a rectangle
Thus, the bisectors of the angles of a parallelogram enclose a rectangle.
Solution:

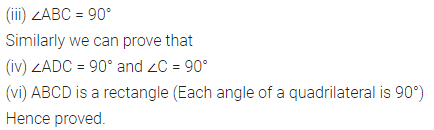
Question 17.
In parallelogram ABCD, X and Y are midpoints of opposite sides AB and DC respectively. Prove that:
(i) AX = YC
(ii) AX is parallel to YC
(iii) AXCY is a parallelogram.
Solution:

Question 18.
The given figure shows a parallelogram ABCD. Points M and N lie in diagonal BD such that DM = BN.

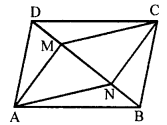
Prove that:
(i) ∆DMC = ∆BNA and so CM = AN
(ii) ∆AMD = ∆CNB and so AM CN
(iii) ANCM is a parallelogram.
Solution:

Question 19.
The given figure shows a rhombus ABCD in which angle BCD = 80°. Find angles x and y.

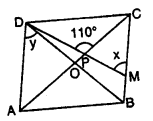
Solution:

Question 20.
Use the information given in the alongside diagram to find the value of x, y and z.

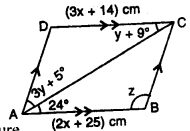
Solution:

Question 21.
The following figure is a rectangle in which x : y = 3 : 7; find the values of x and y.

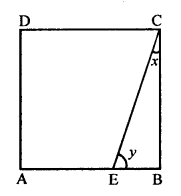
Solution:

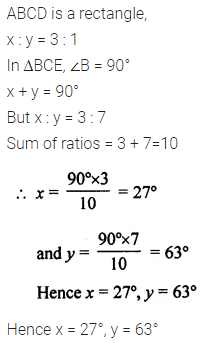
Question 22.
In the given figure, AB || EC, AB = AC and AE bisects ∠DAC. Prove that:

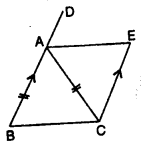
(i) ∠EAC = ∠ACB
(ii) ABCE is a parallelogram.
Solution:

Selina Concise Mathematics Class 8 ICSE Solutions