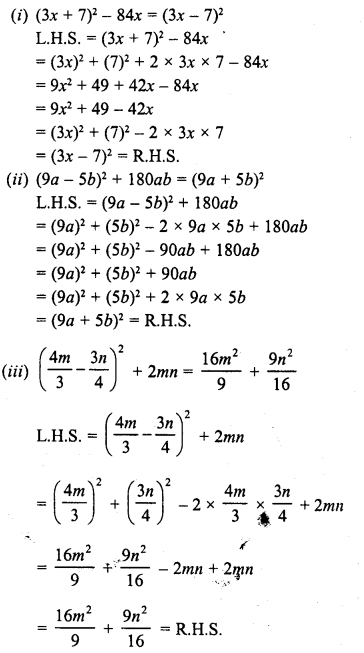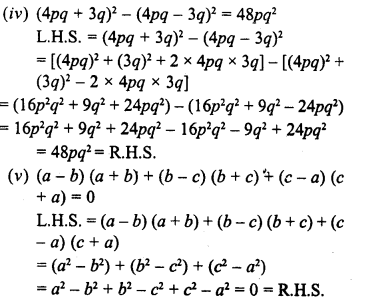RD Sharma Class 8 Solutions Chapter 15 Understanding Shapes I (Polygons) Ex 15.1
These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 15 Understanding Shapes I Ex 15.1
Question 1.
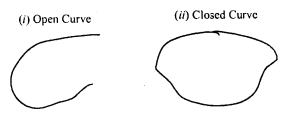
Draw rough diagrams to illustrate the following:
(i) Open curve
(ii) Closed curve
Solution:
Question 2.
Classify the following curves as open or closed.
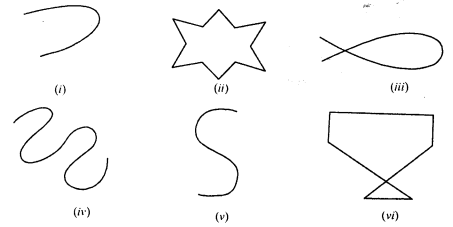
Solution:
Open curves : (i), (iv) and (v) are open curves.
(ii) , (iii), and (vi) are closed curves.
Question 3.
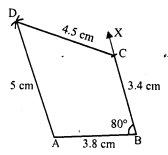
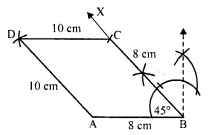
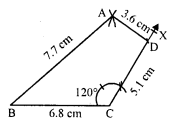
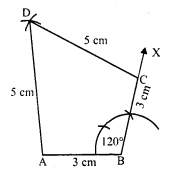
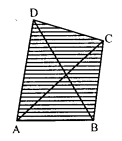
Draw a polygon and shade its interior. Also draw its diagonals, if any.
Solution:
In the given polygon, the shaded portion is its interior region AC and BD are the diagonals of polygon ABCD.
Question 4.
Illustrate, if possible, each one of the following with a rough diagram:
(i) A closed curve that is not a polygon.
(ii) An open curve made up entirely of line segments.
(iii) A polygon with two sides.
Solution:
(i) Close curve but not a polygon.

(ii) An open curve made up entirely of line segments.
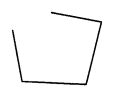
(iii) A polygon with two sides. It is not possible. At least three sides are necessary
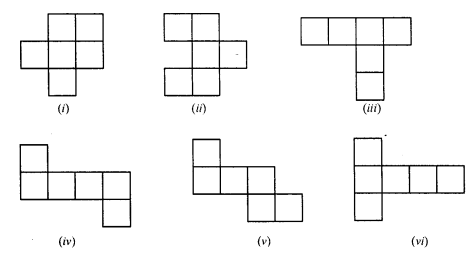
Question 5.
Following are some figures : Classify each of these figures on the basis of the following:
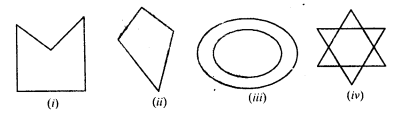
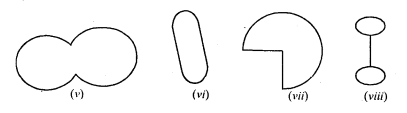
(i) Simple curve
(ii) Simple closed curve
(iii) Polygon
(iv) Convex polygon
(v) Concave polygon
(vi) Not a curve
Solution:
(i) It is a simple closed curve and a concave polygon.
(ii) It is a simple closed curve and convex polygon.
(iii) It is neither a curve nor polygon.
(iv) it is neither a curve not a polygon.
(v) It is a simple closed curve but not a polygon.
(vi) It is a simple closed curve but not a polygon.
(vii) It is a simple closed curve but not a polygon.
(viii) It is a simple closed curve but not a polygon.
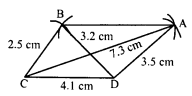
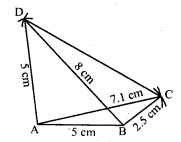
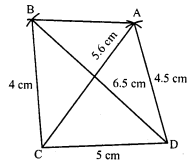
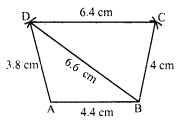
Question 6.
How many diagonals does each of the following have ?
(i) A convex quadrilateral
(ii) A regular hexagon
(iii) A triangle.
Solution:
(i) A convex quadrilateral
Here n = 4
![]()

Question 7.
What is a regular polygon ? State the name of a regular polygon of:
(i) 3 sides
(ii) 4 sides
(iii) 6 sides.
Solution:
A regular polygon is a polygon which has all its sides equal and so all angles are equal,
(i) 3 sides : It is an equilateral triangle.
(ii) 4 sides : It is a square.
(iii) 6 sides : It is a hexagon.
Hope given RD Sharma Class 8 Solutions Chapter 15 Understanding Shapes I Ex 15.1 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.