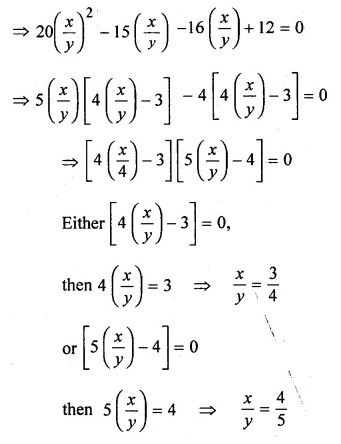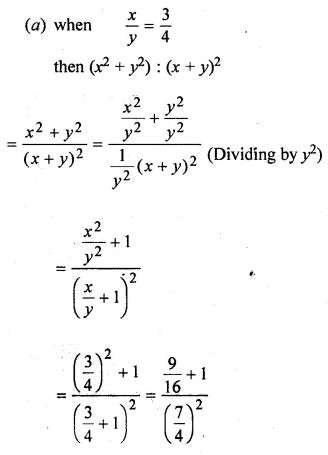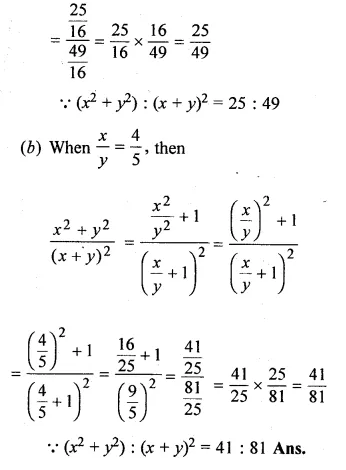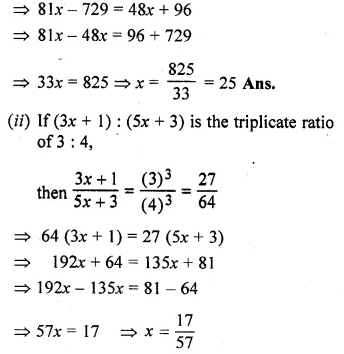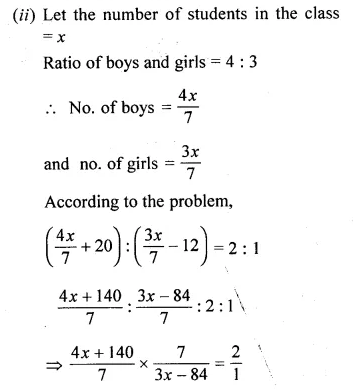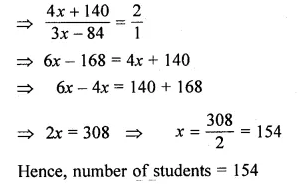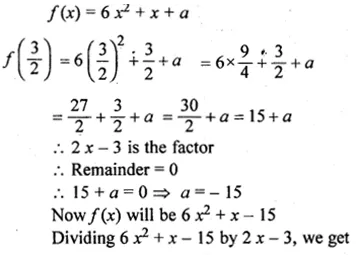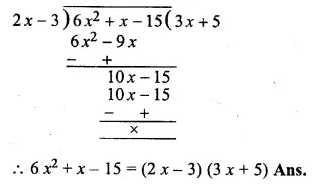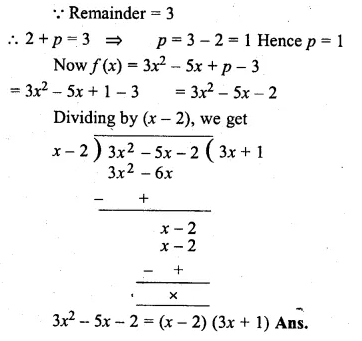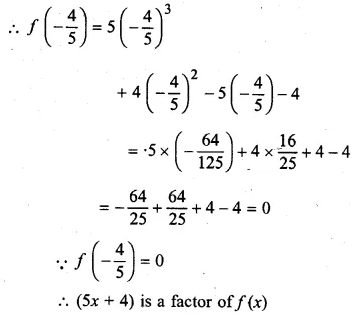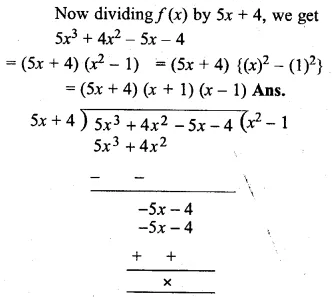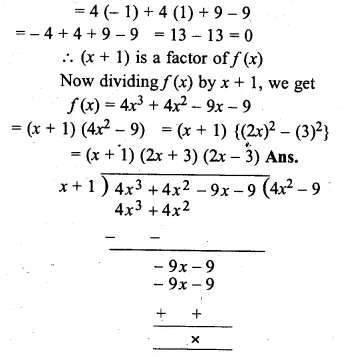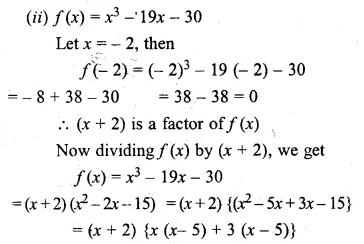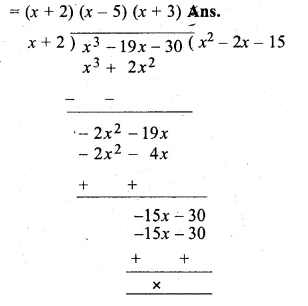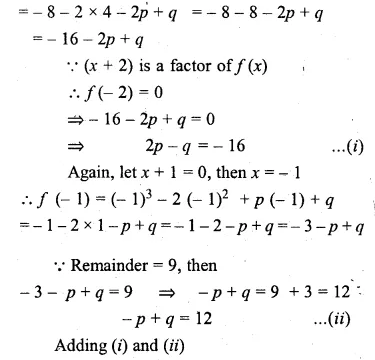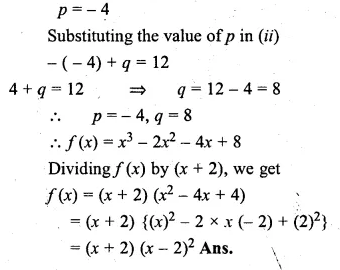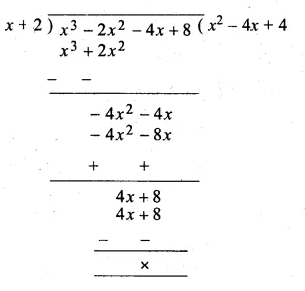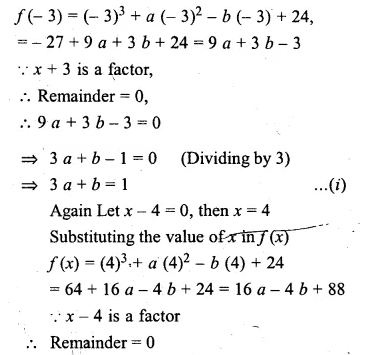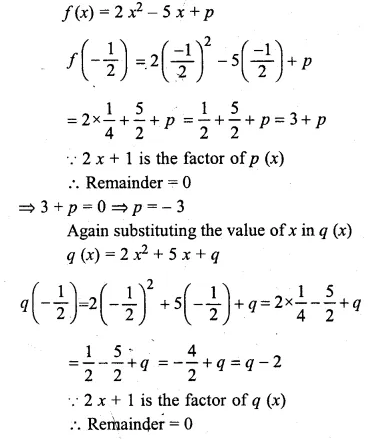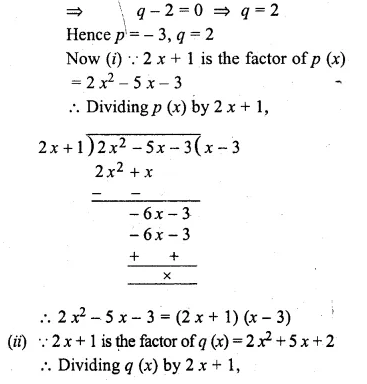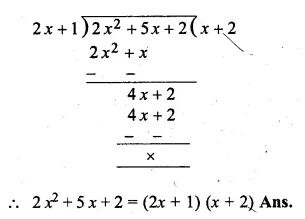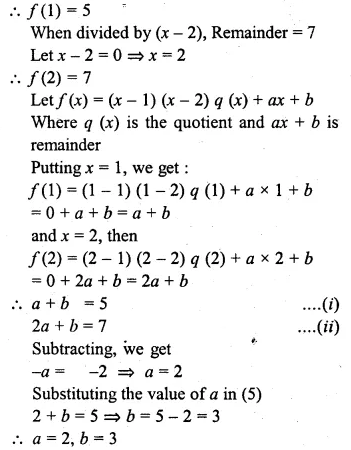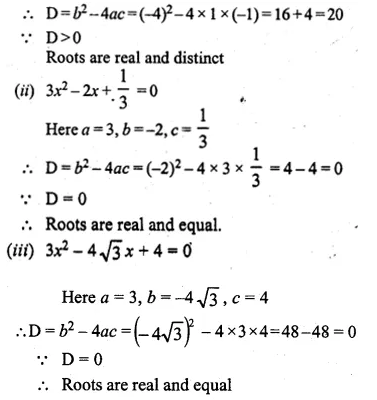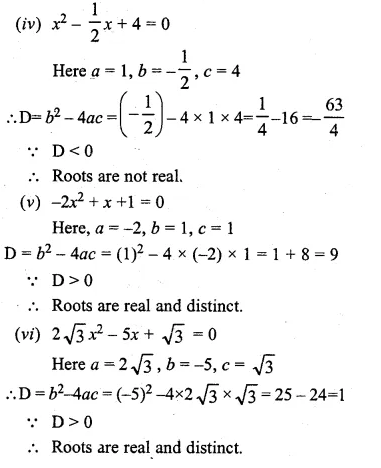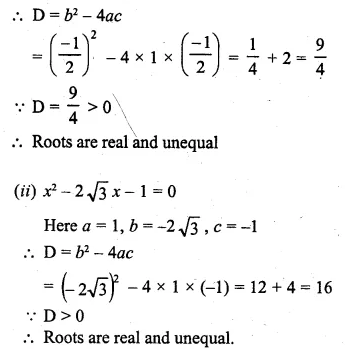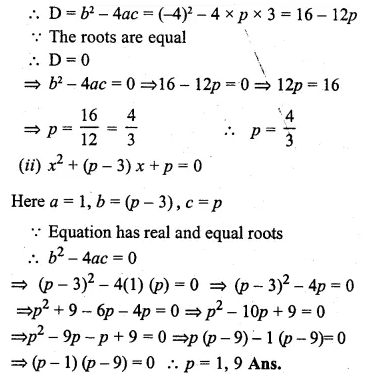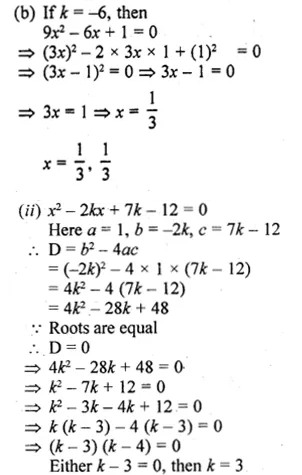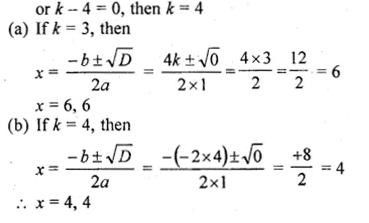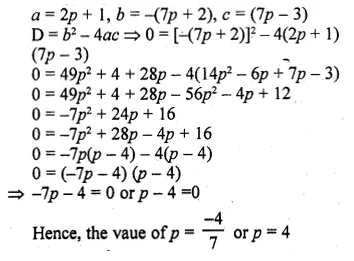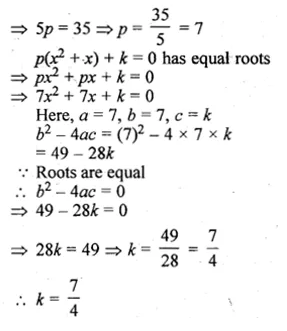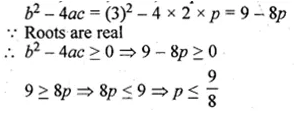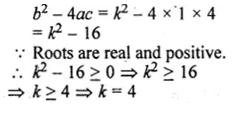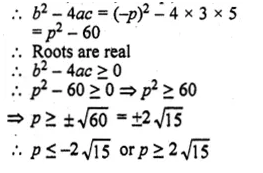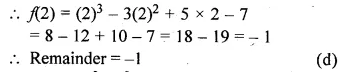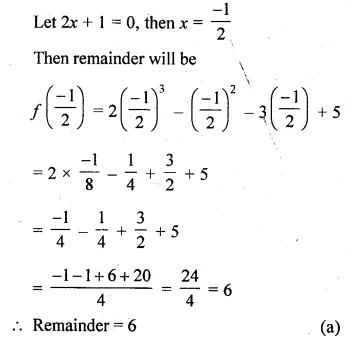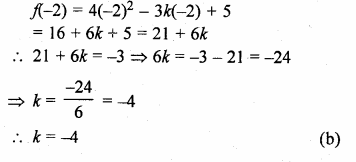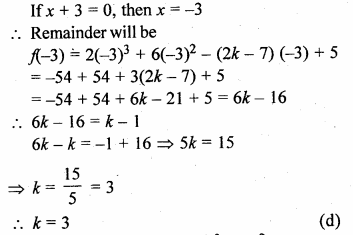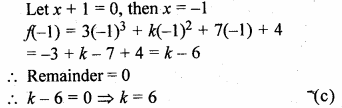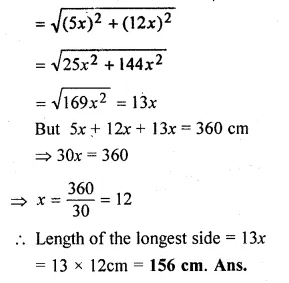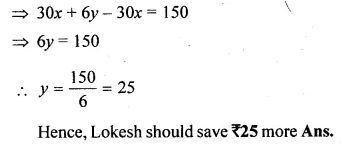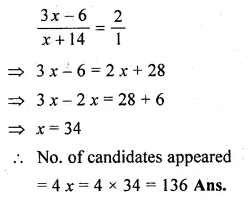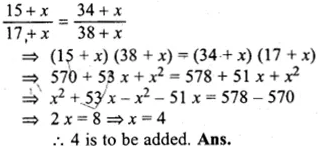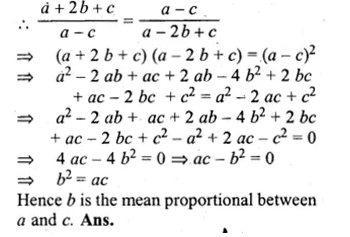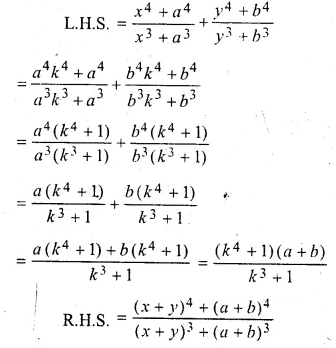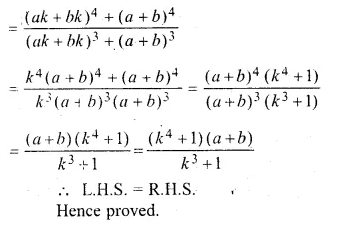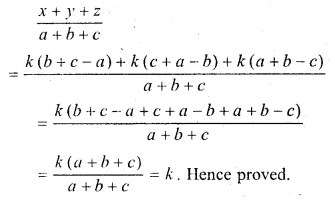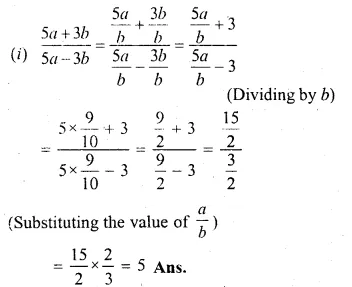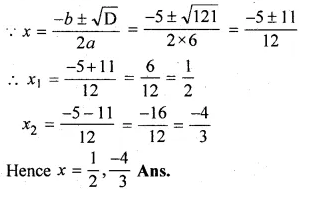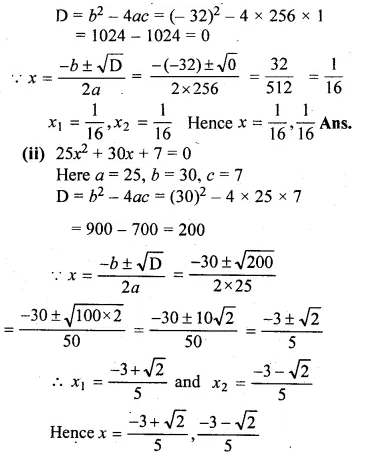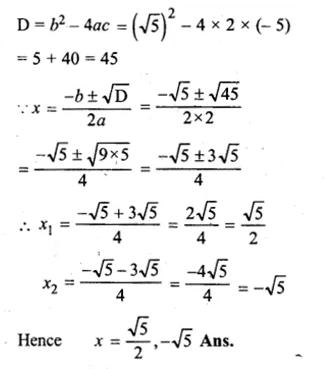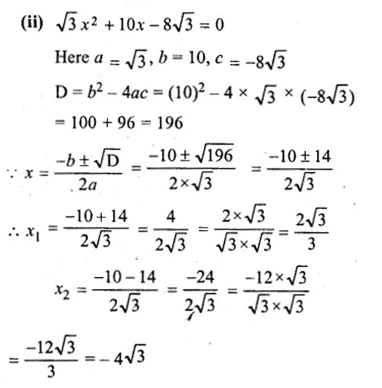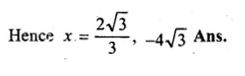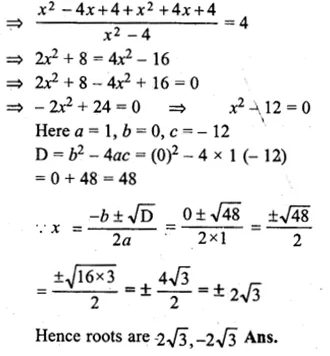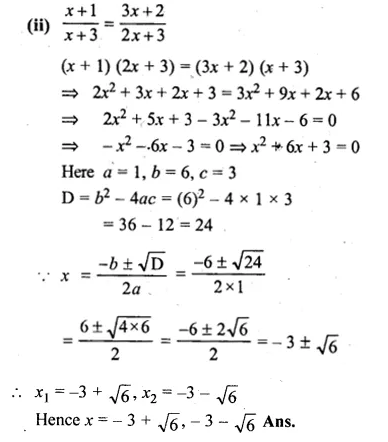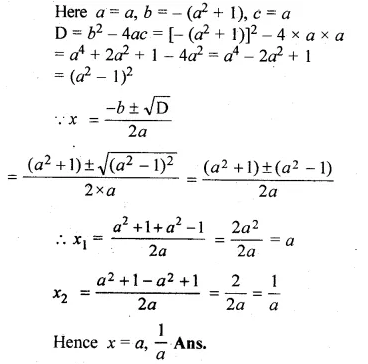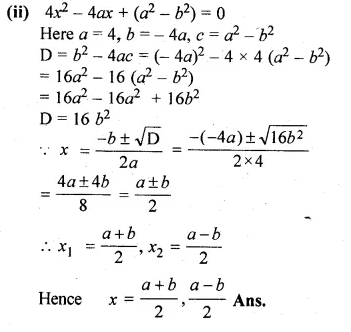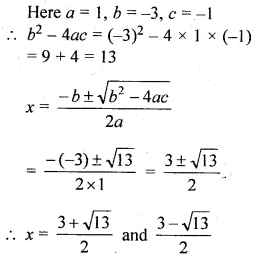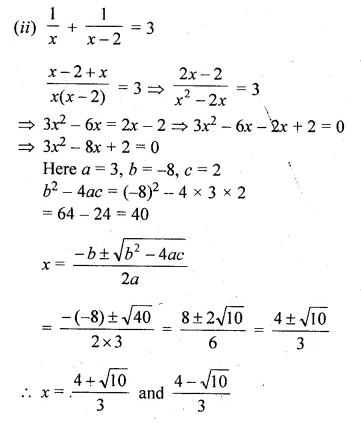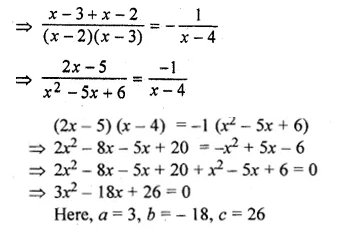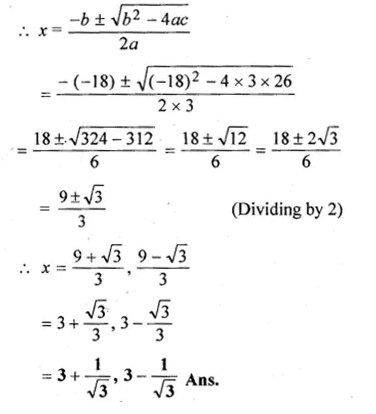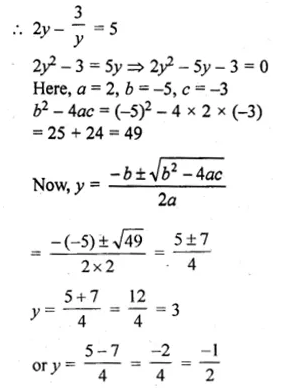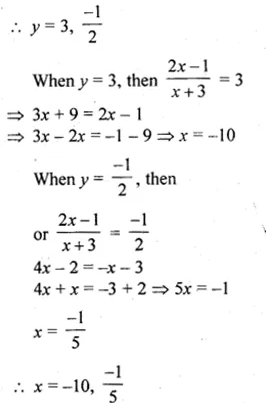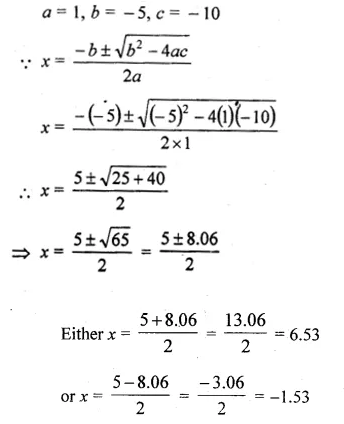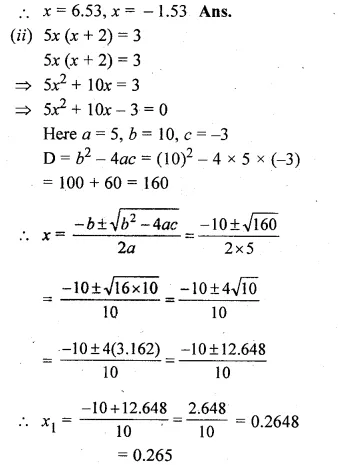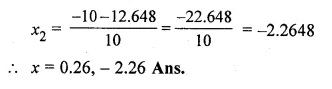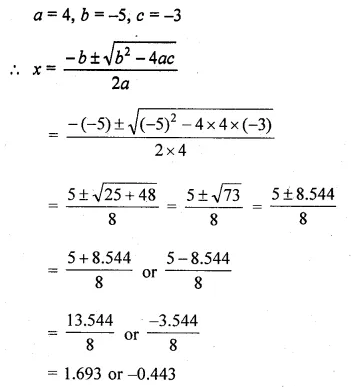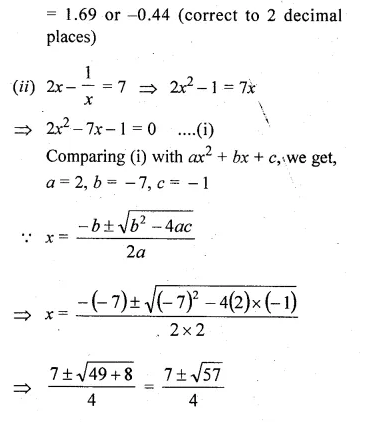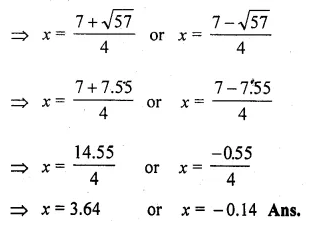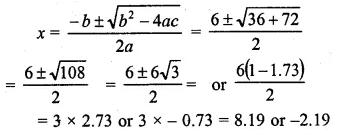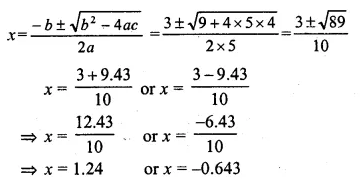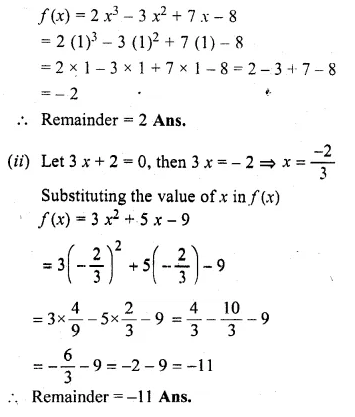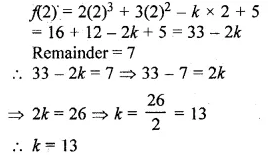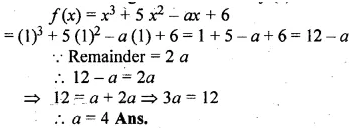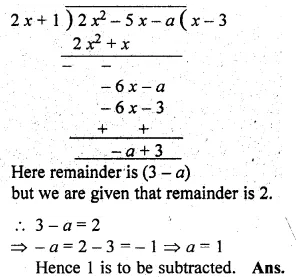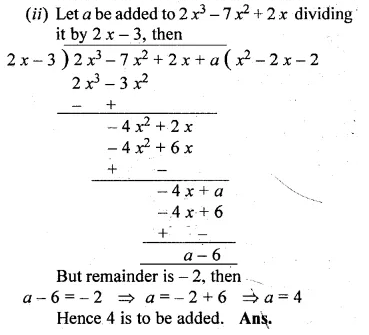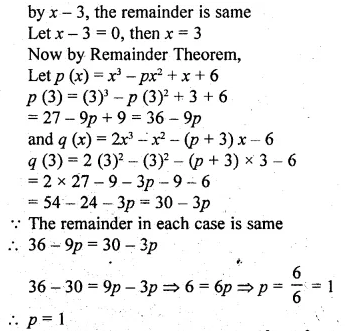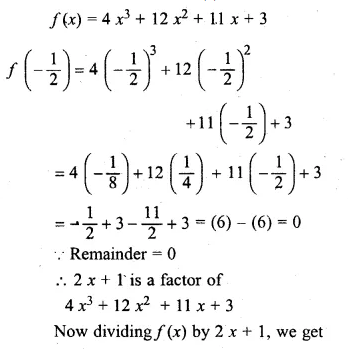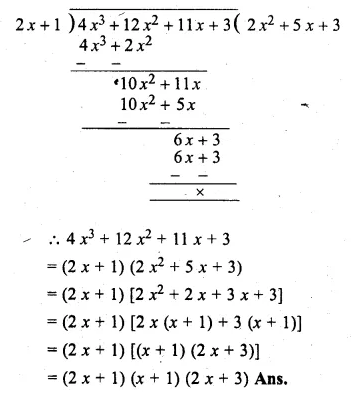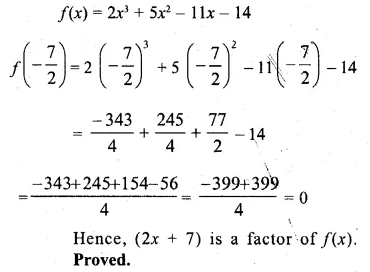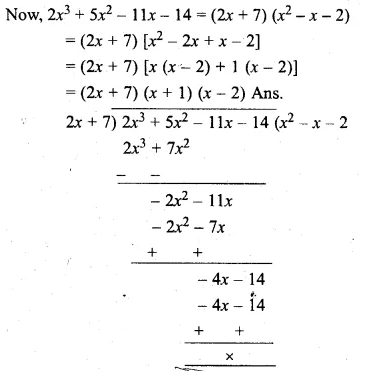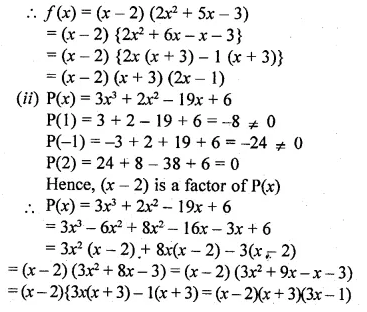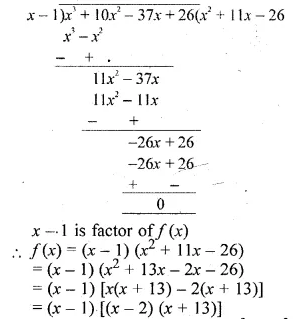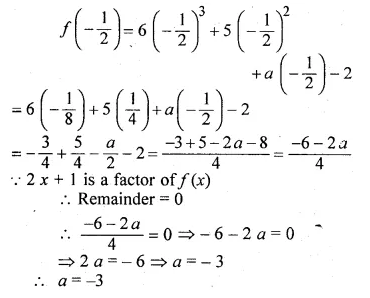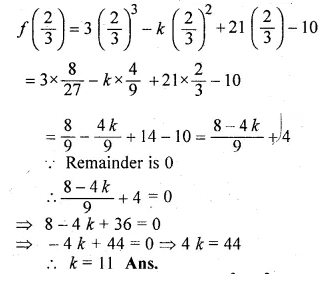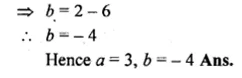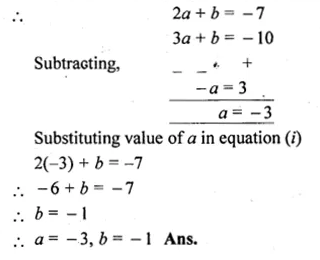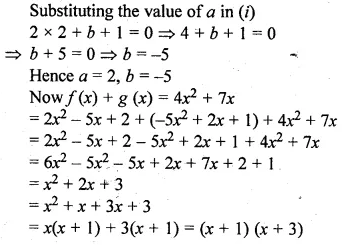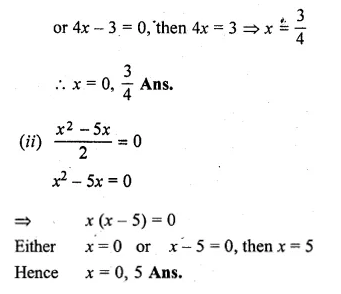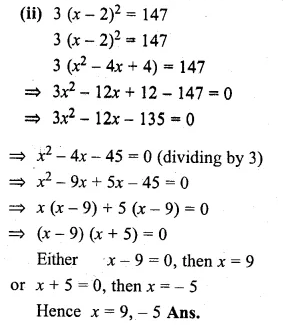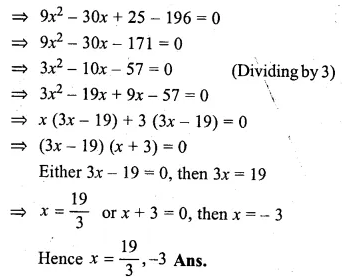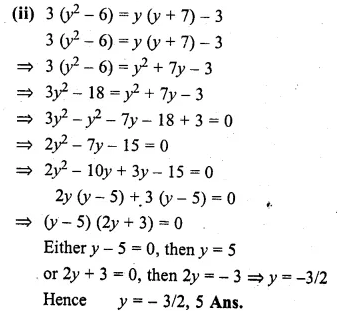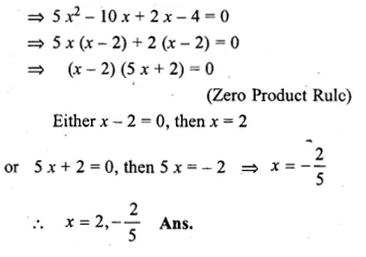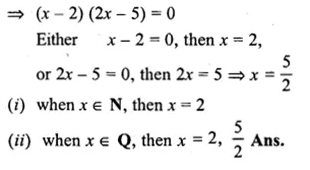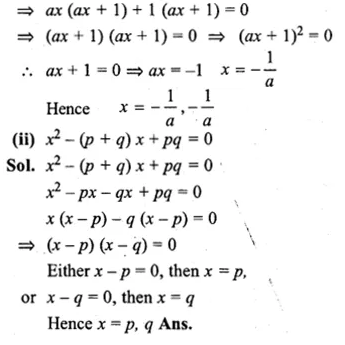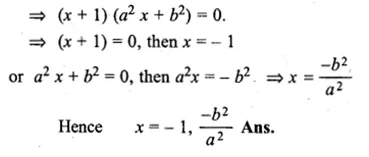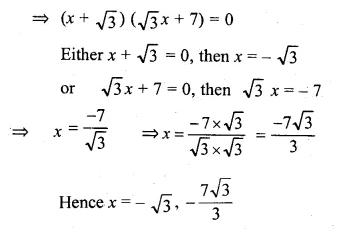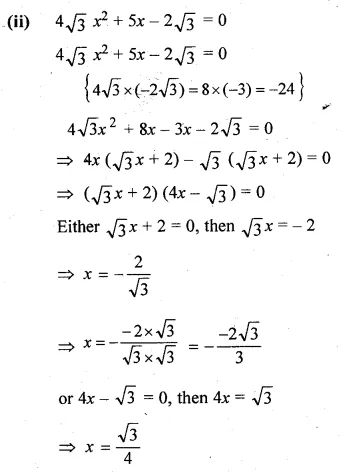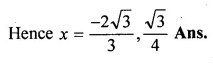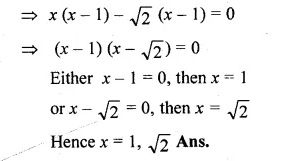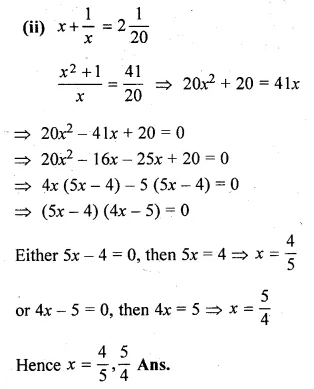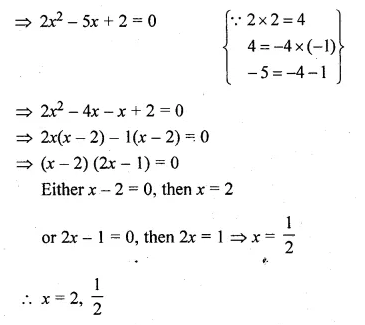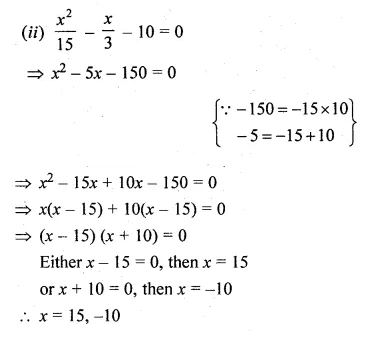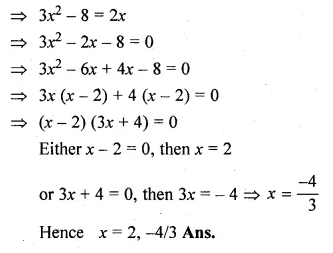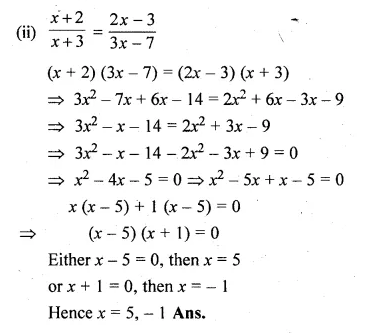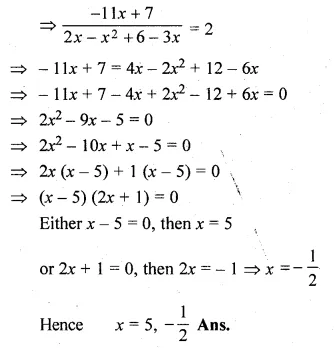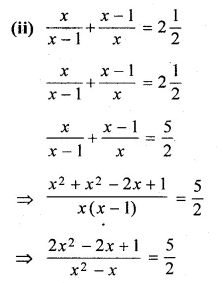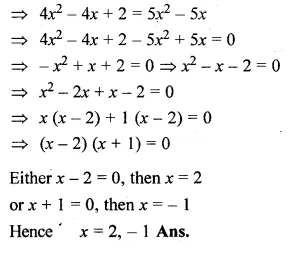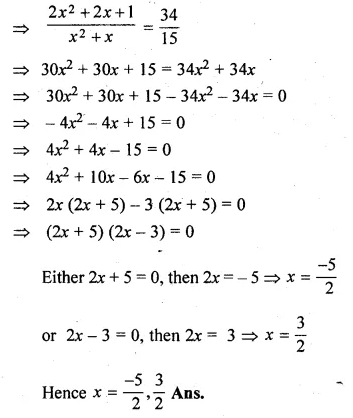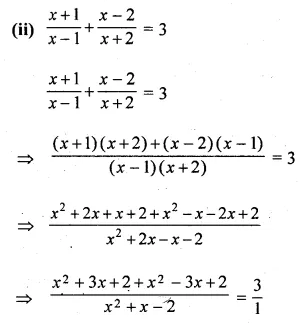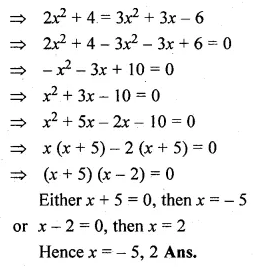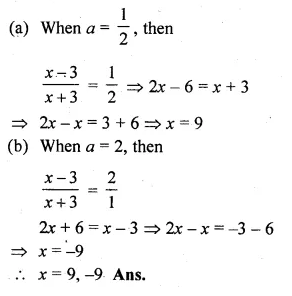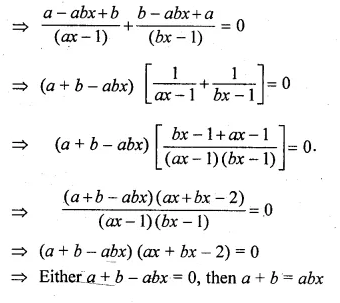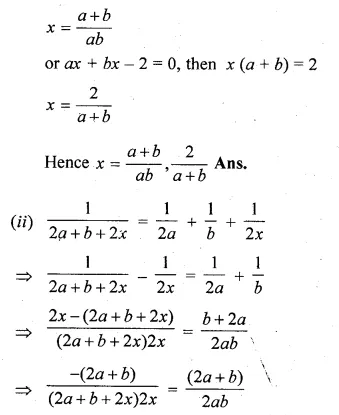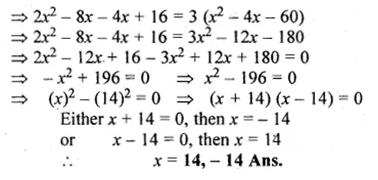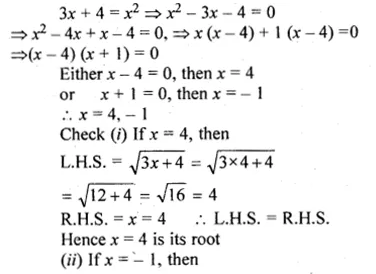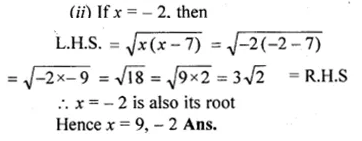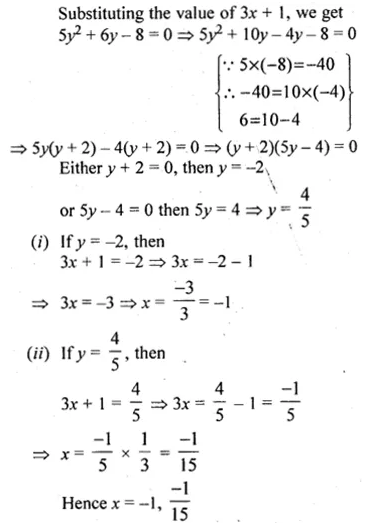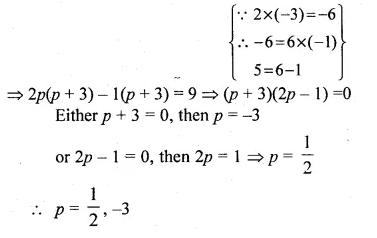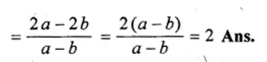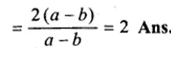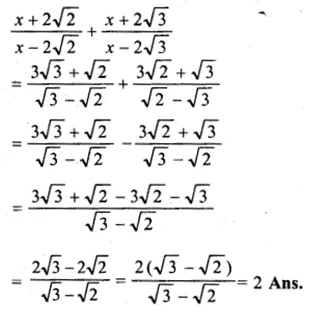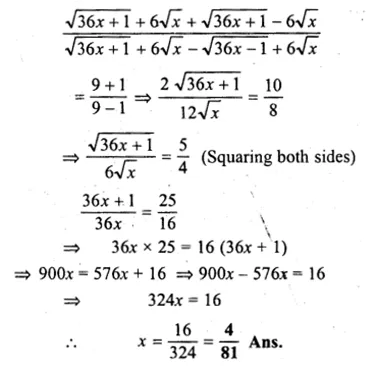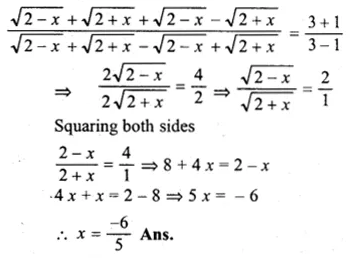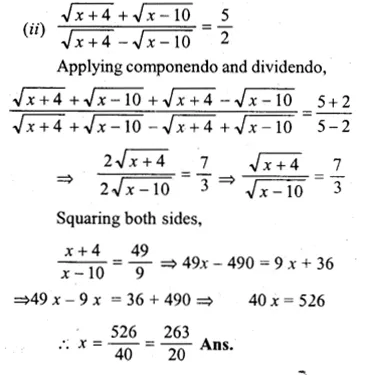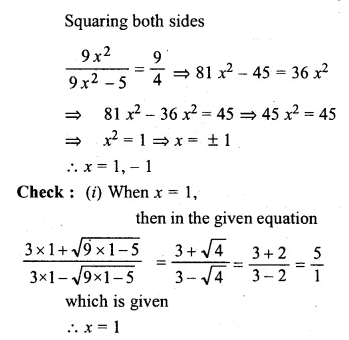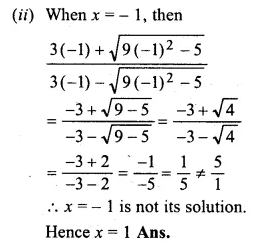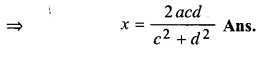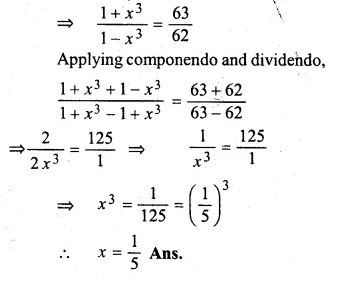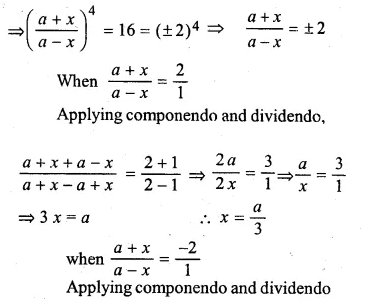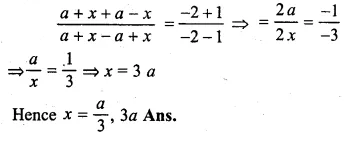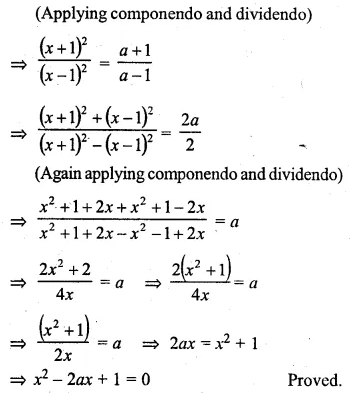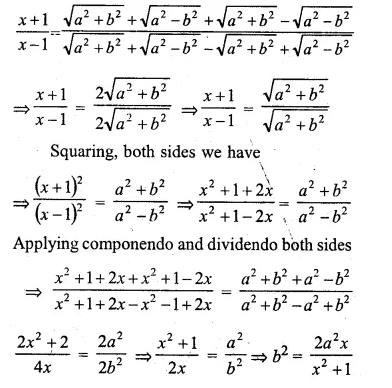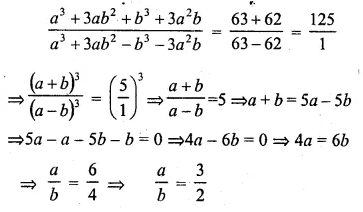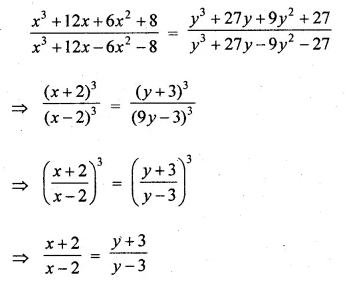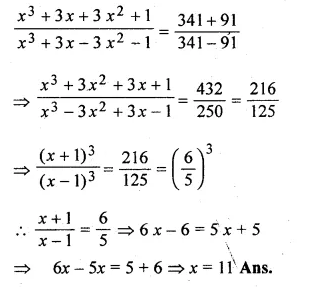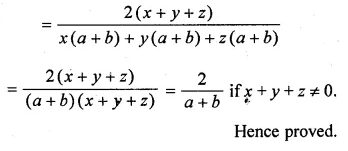Tag: ML Aggarwal Maths for Class 10 ICSE Solutions Pdf Download

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.5

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.5

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Chapter Test

Question 1.
(i) Find two consecutive natural numbers such that the sum of their squares is 61.
(ii) Find two consecutive integers such that the sum of their squares is 61.
Solution:
Let the first natural number = x
then second natural number = x + 1
According to the condition, (x)² + (x + 1)² = 61

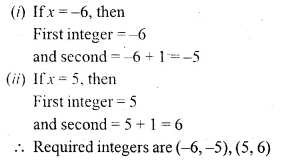
Question 2.
(i) If the product of two positive consecutive even integers is 288, find the integers.
(ii) If the product of two consecutive even integers is 224, find the integers.
(iii) Find two consecutive even natural numbers such that the sum of their squares is 340.
(iv) Find two consecutive odd integers such that the sum of their squares is 394.
Solution:
(i) Let first positive even integer = 2x
then second even integer = 2x + 2
According to the condition,
2x × (2x + 2) = 288
⇒ 4x² + 4x – 288 = 0
⇒ x² + x – 72 = 0 (Dividing by 4)

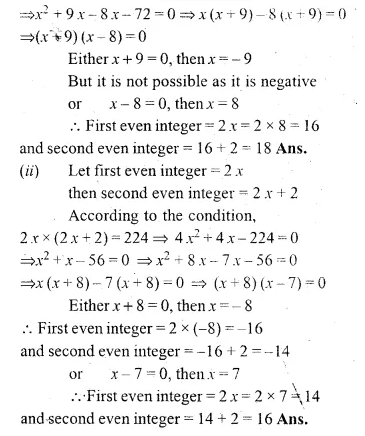
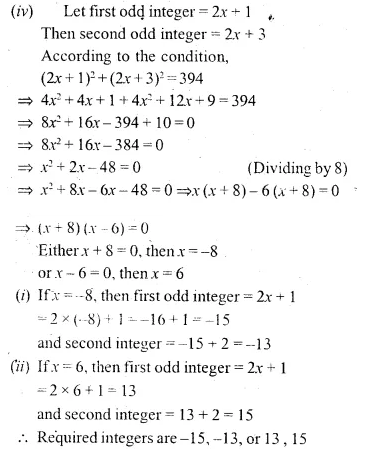
Question 3.
The sum of two numbers is 9 and the sum of their squares is 41. Taking one number as x, form ail equation in x and solve it to find the numbers.
Solution:
Sum of two numbers = 9
Let first number = x
then second number = 9 – x
Now according to the condition,

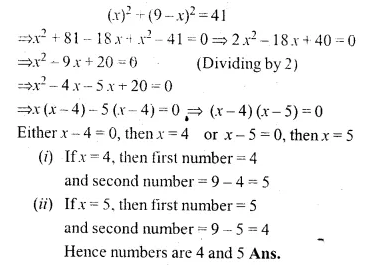
Question 4.
Five times a certain whole number is equal to three less than twice the square of the number. Find the number.
Solution:
Let number = x
Now according to the condition,
5x = 2x² – 3

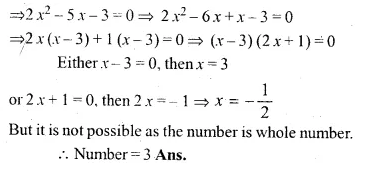
Question 5.
Sum of two natural numbers is 8 and the difference of their reciprocal is 2/15. Find the numbers.
Solution:
Let x and y be two numbers
Given that, x + y = 8 ……(i)

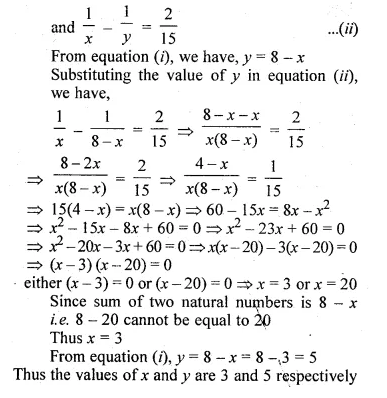
Question 6.
The difference between the squares of two numbers is 45. The square of the smaller number is 4 times the larger number. Determine the numbers.
Solution:
Let the larger number = x
then smaller number = y
Now according to the condition,

Question 7.
There are three consecutive positive integers such that the sum of the square of the first and the product of other two is 154. What are the integers?
Solution:
Let the first integer = x
then second integer = x + 1
and third integer = x + 2
Now according to the condition,

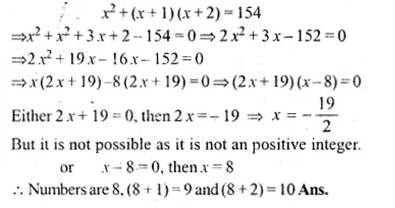
Question 8.
(i) Find three successive even natural numbers, the sum of whose squares is 308.
(ii) Find three consecutive odd integers, the sum of whose squares is 83.
Solution:
(i) Let first even number = 2x
second even number = 2x + 2
third even number = 2x + 4
Now according to the condition,

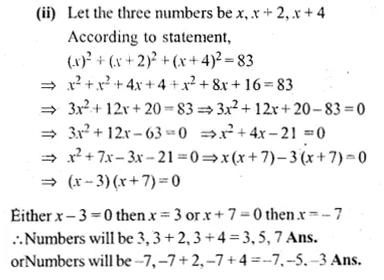
Question 9.
In a certain positive fraction, the denominator is greater than the numerator by 3. If 1 is subtracted from both the numerator and denominator, the fraction is decreased by \(\\ \frac { 1 }{ 14 } \). Find the fraction.
Solution:
Let the numerator of a fraction = x
then denominator = x + 3
then fraction = \(\\ \frac { x }{ x+3 } \)
Now according to the condition,

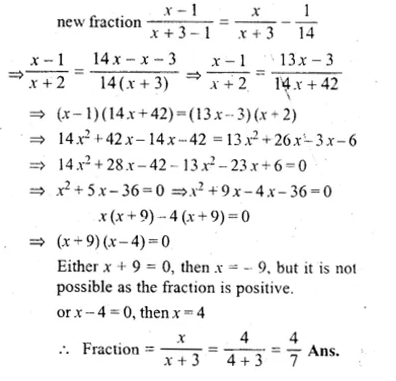
Question 10.
The sum of the numerator and denominator of a certain positive fraction is 8. If 2 is added to both the numerator and denominator, the fraction is increased by \(\\ \frac { 4 }{ 35 } \). Find the fraction.
Solution:
Let the denominator of a positive fraction = x
then numerator = 8 – x

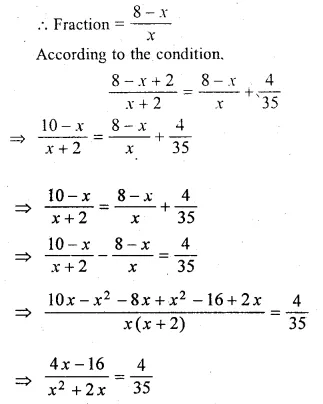
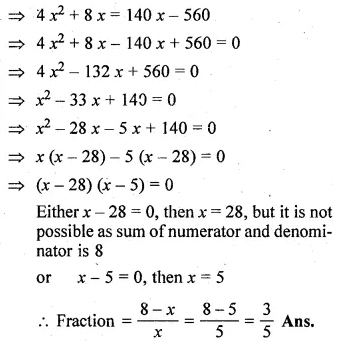
Question 11.
A two digit number contains the bigger at ten’s place. The product of the digits is 27 and the difference between two digits is 6. Find the number.
Solution:
Let unit’s digit = x
then tens digit = x + 6
Number = x + 10(x + 6)
= x + 10x + 60
= 11x + 60

Question 12.
A two digit positive number is such that the product of its digits is 6. If 9 is added to the number, the digits interchange their places. Find the number. (2014)
Solution:
Let 2-digit number = xy = 10x + y
Reversed digits = yx = 10y + x
According to question,

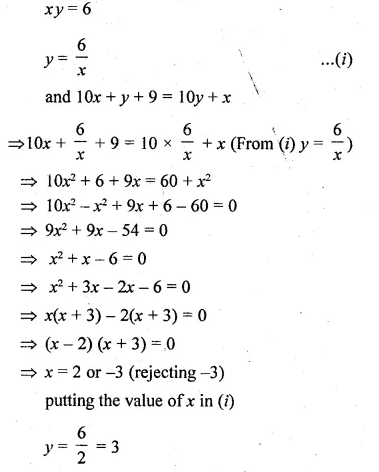
Question 13.
A rectangle of area 105 cm² has its length equal to x cm. Write down its breadth in terms of x. Given that the perimeter is 44 cm, write down an equation in x and solve it to determine the dimensions of the rectangle.
Solution:
Perimeter of rectangle = 44 cm
length + breadth = \(\\ \frac { 44 }{ 2 } \) = 22 cm
Let length = x
then breadth = 22 – x
According to the condition,

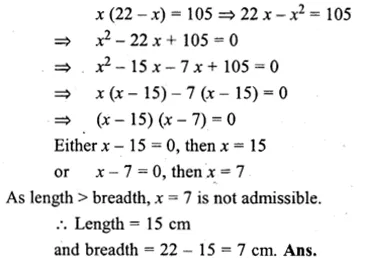
Question 14.
A rectangular garden 10 m by 16 m is to be surrounded by a concrete walk of uniform width. Given that the area of the walk is 120 square metres, assuming the width of the walk to be x, form an equation in x and solve it to find the value of x. (1992)
Solution:
Length of garden = 16 m
and width = 10 m
Let the width of walk = x m
Outer length = 16 + 2x
and outer width = 10 + 2x
Now according to the condition,

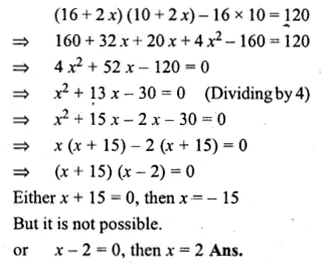
Question 15.
(i) Harish made a rectangular garden, with its length 5 metres more than its width. The next year, he increased the length by 3 metres and decreased the width by 2 metres. If the area of the second garden was 119 sq m, was the second garden larger or smaller ?
(ii) The length of a rectangle exceeds its breadth by 5 m. If the breadth were doubled and the length reduced by 9 m, the area of the rectangle would have increased by 140 m². Find its dimensions.
Solution:
In first case,
Let length of the garden = x m
then width = (x – 5) m
Area = l x b = x(x – 5) sq. m
In second case,

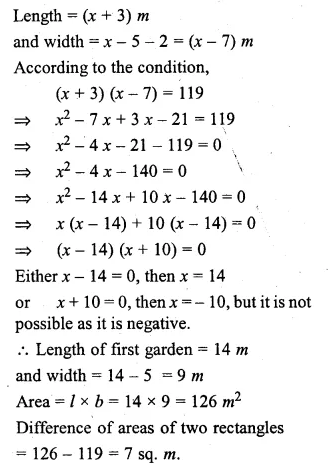
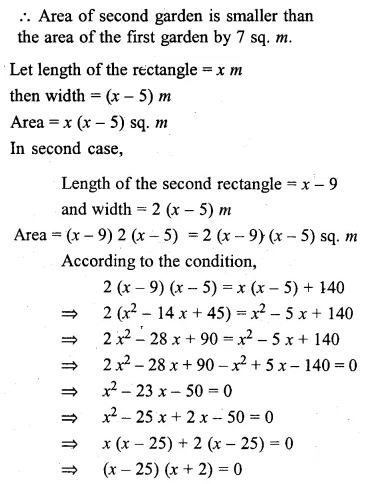
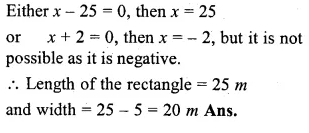
Question 16.
The perimeter of a rectangular plot is 180 m and its area is 1800 m². Take the length of the plot as x m. Use the perimeter 180 m to write the value of the breadth in terms of x. Use the values of length, breadth and the area to write an equation in x. Solve the equation to calculate the length and breadth of the plot. (1993)
Solution:
The perimeter of a rectangular field = 180 m
and area = 1800 m²
Let length = x m

Question 17.
The lengths of the parallel sides of a trapezium are (x + 9) cm and (2x – 3) cm and the distance between them is (x + 4) cm. If its area is 540 cm², find x.
Solution:
Area of a trapezium = \(\\ \frac { 1 }{ 2 } \)
(sum of parallel sides) x height
Lengths of parallel sides are (x + 9) and (2x – 3)
and height = (x + 4)
According to the condition,

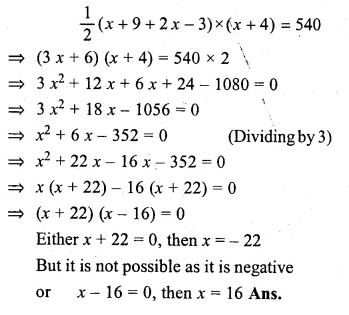
Question 18.
If the perimeter of a rectangular plot is 68 m and the length of its diagonal is 26 m, find its area.
Solution:
Perimeter = 68 m and diagonal = 26 m
Length + breadth = \(\\ \frac { 68 }{ 2 } \) = 34 m
Let length = x m
then breadth = (34 – x) m

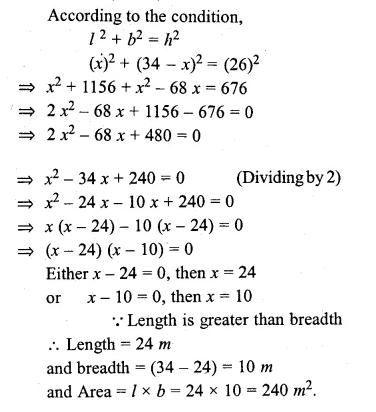
Question 19.
If the sum of two smaller sides of a right – angled triangle is 17cm and the perimeter is 30cm, then find the area of the triangle.
Solution:
The perimeter of the triangle = 30 cm.
Let one of the two small sides = x
then, other side = 17 – x

Question 20.
The hypotenuse of grassy land in the shape of a right triangle is 1 metre more than twice the shortest side. If the third side is 7 metres more than the shortest side, find the sides of the grassy land.
Solution:
Let the shortest side = x
Hypotenuse = 2x + 1
and third side = x + 7
According to the condition,

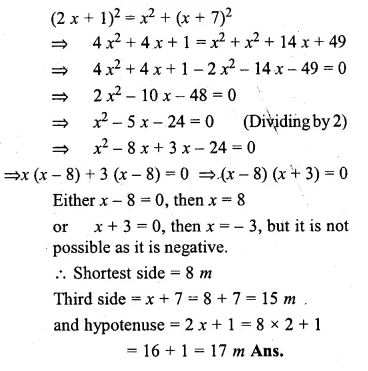
Question 21.
Mohini wishes to fit three rods together in the shape of a right triangle. If the hypotenuse is 2 cm longer than the base and 4 cm longer than the shortest side, find the lengths of the rods.
Solution:
Let the length of hypotenuse = x cm
then base = (x – 2) cm
and shortest side = x – 4
According to the condition,

Question 22.
In a P.T. display, 480 students are arranged in rows and columns. If there are 4 more students in each row than the number of rows, find the number of students in each row.
Solution:
Total number of students = 480
Let the number of students in each row = x

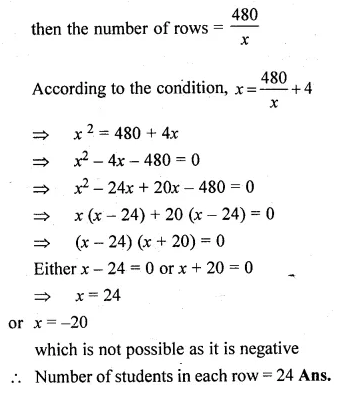
Question 23.
In an auditorium, the number of rows are equal to the number of seats in each row.If the number of rows is doubled and number of seats in each row is reduced by 5, then the total number of seats is increased by 375. How many rows were there?
Solution:
Let the number of rows = x
then no. of seats in each row = x
and total number of seats = x × x = x²
According to the condition,

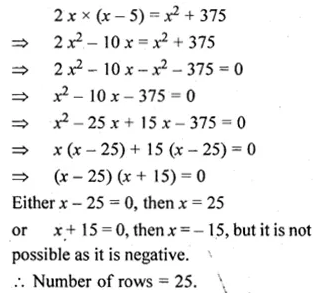
Question 24.
At an annual function of a school, each student gives the gift to every other student. If the number of gifts is 1980, find the number of students.
Solution:
Let the number of students = x
then the number of gifts given = x – 1
Total number of gifts = x (x – 1)
According to the condition,
x (x – 1) = 1980

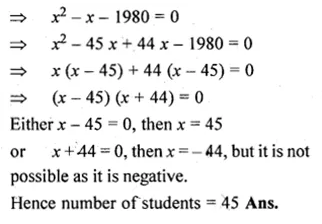
Question 25.
A bus covers a distance of 240 km at a uniform speed. Due to heavy rain, its speed gets reduced by 10 km/h and as such it takes two hours longer to cover the total distance. Assuming the uniform speed to be ‘x’ km/h, form an equation and solve it to evaluate x. (2016)
Solution:
Distance = 240 km
Let speed of a bus = x km/hr

Question 26.
The speed of an express train is x km/hr and the speed of an ordinary train is 12 km/hr less than that of the express train. If the ordinary train takes one hour longer than the express train to cover a distance of 240 km, find the speed of the express train.
Solution:
Let the speed of express train = x km
Then speed of the ordinary train = (x – 12) km
Time is taken to cover 240 km by the express

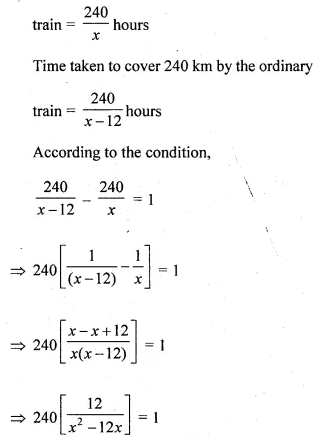
Question 27.
A car covers a distance of 400 km at a certain speed. Had the speed been 12 km/h more, the time taken for the journey would have been 1 hour 40 minutes less. Find the original speed of the car. (1996)
Solution:
Let the original speed of the car = x km/h.
Distance covered = 400 km

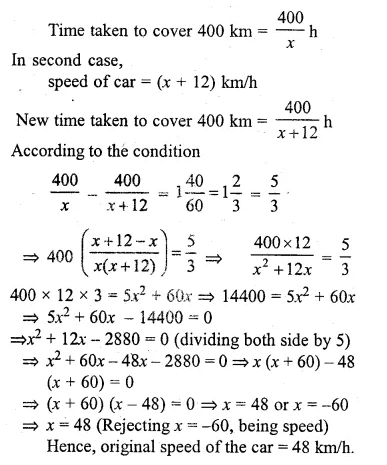
Question 28.
An aeroplane travelled a distance of 400 km at an average speed of x km/hr. On the return journey, the speed was increased by 40 km/hr. Write down an expression for the time taken for
(i)the onward journey,
(ii) the return journey.
If the return journey took 30 minutes less than the onward journey, write down an equation in x and find its value. (2002)
Solution:
Distance = 400 km
Speed of aeroplane = x km/hr

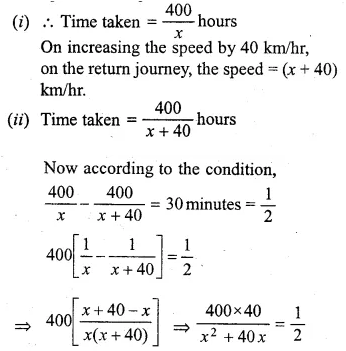
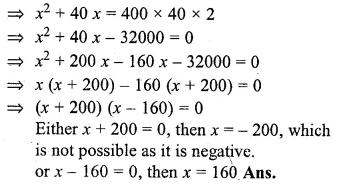
Question 29.
The distance by road between two towns A and B, is 216 km, and by rail it is 208 km. A car travels at a speed of x km/hr, and the train travels at a speed which is 16 km/hr faster than the car. Calculate :
(i) The time taken by the car, to reach town B from A, in terms of x ;
(ii) The time taken by the train, to reach town B from A, in terms of x ;
(iii) If the train takes 2 hours less than the car, to reach town B, obtain an equation in x and solve it.
(iv) Hence find the speed of the train. (1998)
Solution:
The distance by road between A and B = 216 km
and the distance by rail = 208 km
speed of car = x km/hr

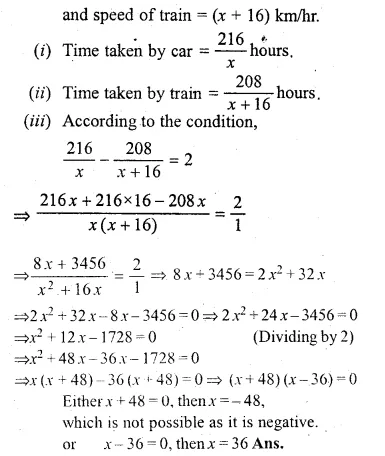
Question 30.
An aeroplane flying with a wind of 30 km/hr takes 40 minutes less to fly 3600 km, than what it would have taken to fly against the same wind. Find the planes speed of flying in still air.
Solution:
Let the speed of the plane in still air = x km/hr
Speed of wind = 30 km/hr
Distance = 3600 km

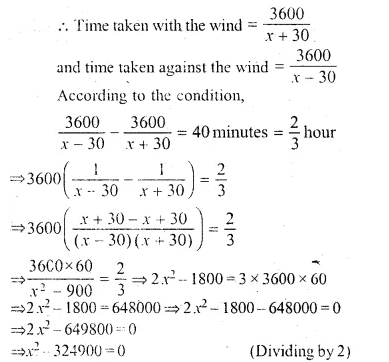
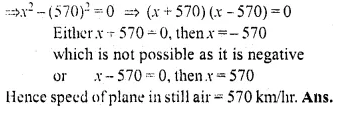
Question 31.
A school bus transported an excursion party to a picnic spot 150 km away. While returning, it was raining and the bus had to reduce its speed by 5 km/hr, and it took one hour longer to make the return trip. Find the time taken to return.
Solution:
Distance = 150 km
Let the speed of bus = x km/hr

Question 32.
A boat can cover 10 km up the stream and 5 km down the stream in 6 hours. If the speed of the stream is 1.5 km/hr. find the speed of the boat in still water.
Solution:
Distance up stream = 10 km
and down stream = 5 km
Total time is taken = 6 hours
Speed of stream = 1.5 km/hr
Let the speed of a boat in still water = x km/hr
According to the condition,

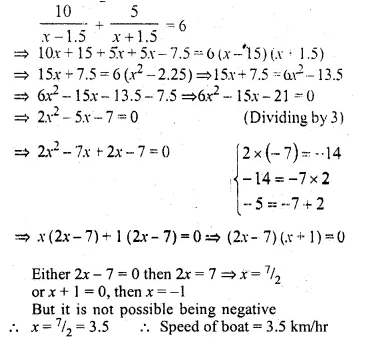
Question 33.
Two pipes running together can fill a tank in \({ 11 }^{ 1/9 }\) minutes. If one pipe takes 5 minutes more than the other to fill the tank, find the time in which each pipe would/fill the tank.
Solution:
Let the time taken by one pipe = x minutes
Then time taken by second pipe = (x + 5) minutes
Time taken by both pipes = \({ 11 }^{ 1/9 }\) minutes
Now according to the condition.

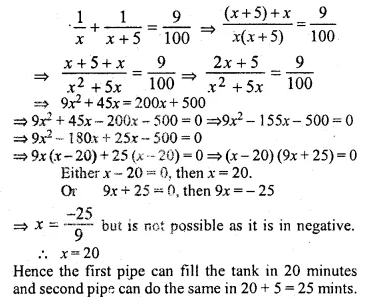
Question 34.
(i) Rs. 480 is divided equally among ‘x’ children. If the number of children was 20 more then each would have got Rs. 12 less. Find ‘x’.
(ii) Rs. 6500 is divided equally among a certain number of persons. Had there been 15 more persons, each would have got Rs. 30 less. Find the original number of persons.
Solution:
(i) Share of each child = Rs \(\\ \frac { 480 }{ x } \)
According to the question

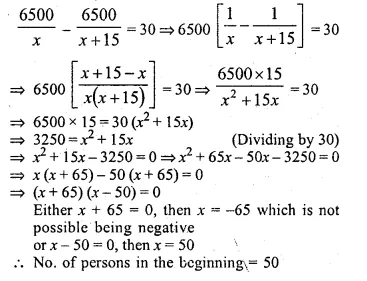
Question 35.
2x articles cost Rs. (5x + 54) and (x + 2) similar articles cost Rs. (10x – 4), find x.
Solution:
Cost of 2x articles = 5x + 54
Cost of 1 article = \(\\ \frac { 5x+54 }{ 2x } \) ….(i)
Again cost of x + 2 articles = 10x – 4

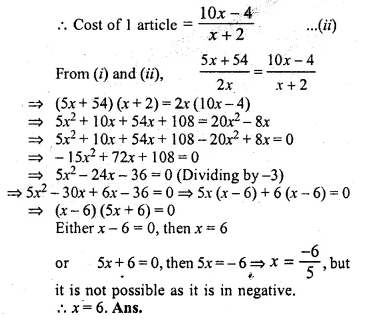
Question 36.
A trader buys x articles for a total cost of Rs. 600.
(i) Write down the cost of one article in terms of x. If the cost per article were Rs. 5 more, the number of articles that can be bought for Rs. 600 would be four less.
(ii) Write down the equation in x for the above situation and solve it to find x. (1999)
Solution:
Total cost = Rs. 600,
No. of articles = x

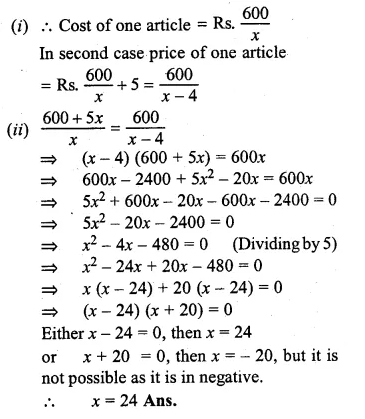
Question 37.
A shopkeeper buys a certain number of books for Rs 960. If the cost per book was Rs 8 less, the number of books that could be bought for Rs 960 would be 4 more. Taking the original cost of each book to be Rs x, write an equation in x and solve it to find the original cost of each book.
Solution:
Let original cost = Rs x
No. of books bought = \(\\ \frac { 960 }{ x } \)
New cost of books = Rs (x – 8)

Question 38.
A piece of cloth costs Rs. 300. If the piece was 5 metres longer and each metre of cloth costs Rs. 2 less, the cost of the piece would have remained unchanged. How long is the original piece of cloth and what is the rate per metre?
Solution:
The total cost of cloth piece = Rs. 300
Let the length of the piece of cloth in the beginning = x m

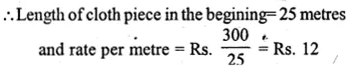
Question 39.
The hotel bill for a number of people for an overnight stay is Rs. 4800. If there were 4 more, the bill each person had to pay would have reduced by Rs. 200. Find the number of people staying overnight. (2000)
Solution:
Let the number of people = x
Amount of bill = Rs. 4800

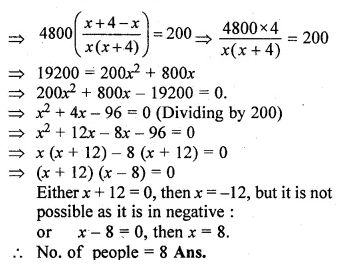
Question 40.
A person was given Rs. 3000 for a tour. If he extends his tour programme by 5 days, he must cut down his daily expenses by Rs. 20. Find the number of days of his tour programme.
Solution:
Let the number of days of tour programme = x
Amount = Rs. 3000

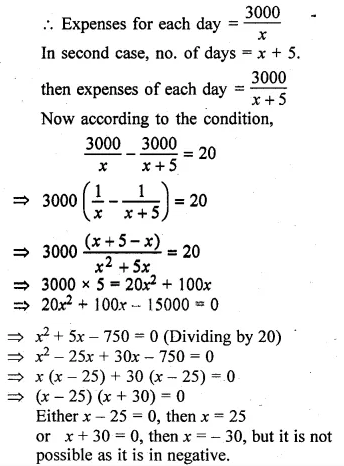
Question 41.
Ritu bought a saree for Rs. 60 x and sold it for Rs. (500 + 4x) at a loss of x%. Find the cost price.
Solution:
The cost price of saree = Rs. 60x
and selling price = Rs. (500 + 4x)
Loss = x%
Now according to the condition

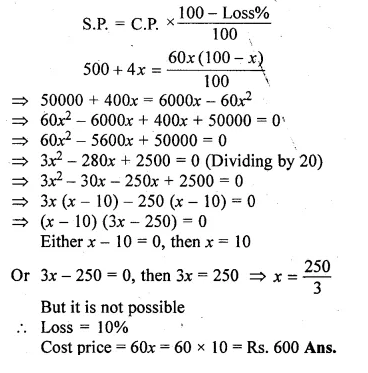
Question 42.
(i) The sum of the ages of Vivek and his younger brother Amit is 47 years. The product of their ages in years is 550. Find their ages. (2017)
(ii) Paul is x years old and his father’s age is twice the square of Paul’s age. Ten years hence, the father’s age will be four times Paul’s age. Find their present ages.
Solution:
(i) Let Vivek’s present age be x years.
His brother’s age = (47 – x) years
According to question,
x(47 – x) = 550
⇒ 47x – x² = 550
⇒ x² – 47x + 550 = 0
⇒ x² – 25x – 22x + 550 = 0
⇒ x(x – 25) – 22(x – 25) – 0

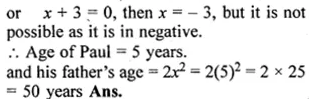
Question 43.
The age of a man is twice the square of the age of his son. Eight years hence, the age of the man will be 4 years more than three times the age of his son. Find the present age.
Solution:
Let the present age of the son = x years
then, the present age of the man = 2x² years.
8 years hence,
The age of son will be = (x + 8) years and the
age of man = (2x² + 8) years
According to the problem,

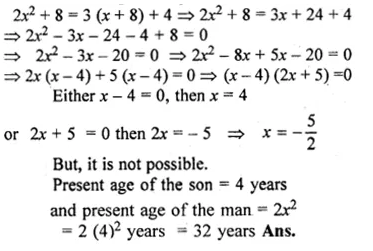
Question 44.
Two years ago, a man’s age was three times the square of his daughter’s age. Three years hence, his age will be four times his daughter’s age. Find their present ages.
Solution:
2 years ago,
Let the age of daughter = x
age of man = 3x²
then present age of daughter = x + 2
and mean = 3x² + 2

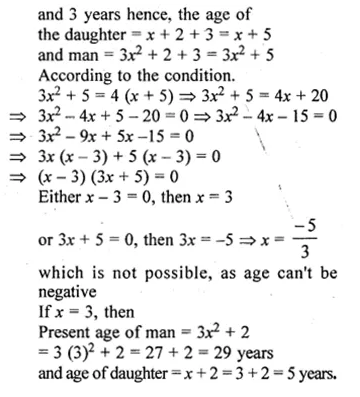
Question 45.
The length (in cm) of the hypotenuse of a right-angled triangle exceeds the length of one side by 2 cm and exceeds twice the length of another side by 1 cm. Find the length of each side. Also, find the perimeter and the area of the triangle.
Solution:
Let the length of one side = x cm
and other side = y cm.
then hypotenues = x + 2, and 2y + 1

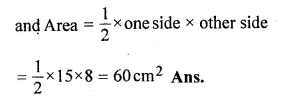
Question 46.
If twice the area of a smaller square is subtracted from the area of a larger square, the result is 14 cm². However, if twice the area of the larger square is added to three times the area of the smaller square, the result is 203 cm². Determine the sides of the two squares.
Solution:
Let the side of smaller square = x cm
and side of bigger square = y cm
According to the condition,

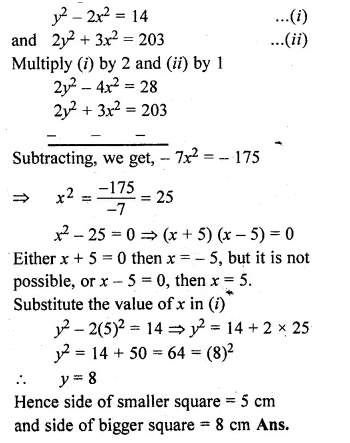
Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.5 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.1

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.1

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Chapter Test

Question 1.
An alloy consists of \(27 \frac { 1 }{ 2 } \) kg of copper and \(2 \frac { 3 }{ 4 } \) kg of tin. Find the ratio by weight of tin to the alloy
Solution:
Copper = \(27 \frac { 1 }{ 2 } \) kg = \(\\ \frac { 55 }{ 2 } \) kg,
Tin = \(2 \frac { 3 }{ 4 } \) kg = \(\\ \frac { 11 }{ 4 } \) kg

Question 2.
Find the compounded ratio of:
(i) 2 : 3 and 4 : 9
(ii) 4 : 5, 5 : 7 and 9 : 11
(iii) (a – b) : (a + b), (a + b)² : (a² + b²) and (a⁴ – b⁴) : (a² – b²)²
Solution:
(i) 2 : 3 and 4 : 9
Compound ratio = \(\\ \frac { 2 }{ 3 } \) x \(\\ \frac { 4 }{ 9 } \)
= \(\\ \frac { 8 }{ 27 } \) or 8 : 27
(ii) 4 : 5, 5 : 7 and 9 : 11

Question 3.
Find the duplicate ratio of
(i) 2 : 3
(ii) √5 : 7
(iii) 5a : 6b
Solution:
(i) Duplicate ratio of 2 : 3 = (2)² : (3)² = 4 : 9
(ii) Duplicate ratio of √5 : 7 = (√5)² : (7)² = 5 : 49
(iii) Duplicate ratio of 5a : 6b = (5a)² : (6b)² = 25a² : 36b²

Question 4.
Find the triplicate ratio of
(i) 3 : 4
(ii) \(\\ \frac { 1 }{ 2 } \) : \(\\ \frac { 1 }{ 3 } \)
(iii) 1³ : 2³
Solution:
(i) Triplicate ratio of 3 : 4
= (3)³ : (4)³
= 27 : 64

Question 5.
Find the sub-duplicate ratio of
(i) 9 : 16
(ii) \(\\ \frac { 1 }{ 4 } \) : \(\\ \frac { 1 }{ 9 } \),
(iii) 9a² : 49b²
Solution:
(i) Sub-duplicate ratio of 9 : 16
= √9 : √16
= 3 : 4

Question 6.
Find the sub-triplicate ratio of
(i) 1 : 216
(ii) \(\\ \frac { 1 }{ 8 } \) : \(\\ \frac { 1 }{ 125 } \)
(iii) 27a³ : 64b³
Solution:
(i) Sub-triplicate ratio of 1 : 216
= \(\sqrt [ 3 ]{ 1 } :\sqrt [ 3 ]{ 216 } \)

Question 7.
Find the reciprocal ratio of
(i) 4 : 7
(ii) 3² : 4²
(iii) \(\frac { 1 }{ 9 } :2 \)
Solution:
(i) Reciprocal ratio of 4 : 7 = 7 : 4
(ii) Reciprocal ratio of 3² : 4² = 4² : 3² = 16 : 9
(iii) Reciprocal ratio of \(\frac { 1 }{ 9 } :2 \) = \(2:\frac { 1 }{ 9 } \) = 18 : 1

Question 8.
Arrange the following ratios in ascending order of magnitude:
2 : 3, 17 : 21, 11 : 14 and 5 : 7
Solution:
Writing the given ratios in fraction
\(\frac { 2 }{ 3 } ,\frac { 17 }{ 21 } ,\frac { 11 }{ 14 } ,\frac { 5 }{ 7 } \)

Question 9.
(i) If A : B = 2 : 3, B : C = 4 : 5 and C : D = 6 : 7, find A : D
(ii) If x : y = 2 : 3, and y : z = 4 : 7, find x : y : z
Solution:
Let A : B = 2 : 3, B : C = 4 : 5 and C : D = 6 : 7
\(\frac { A }{ B } =\frac { 2 }{ 3 } ,\frac { B }{ C } =\frac { 4 }{ 5 } ,\frac { C }{ D } =\frac { 6 }{ 7 } \)

Question 10.
(i) If A: B = \(\frac { 1 }{ 4 } :\frac { 1 }{ 5 } \) and B : C = \(\frac { 1 }{ 7 } :\frac { 1 }{ 6 } \), find A : B : C.
(ii) If 3A = 4B = 6C, find A : B : C
Solution:
A : B = \(\frac { 1 }{ 4 } \times \frac { 5 }{ 1 } =\frac { 5 }{ 4 } \)
B : C = \(\frac { 1 }{ 7 } \times \frac { 6 }{ 1 } =\frac { 6 }{ 7 } \)

Question 11.
(i) If \(\frac { 3x+5y }{ 3x-5y } =\frac { 7 }{ 3 } \) , Find x : y
(ii) ) If a : b = 3 : 11, find (15a – 3b) : (9a + 5b). a
Solution:
(i) \(\frac { 3x+5y }{ 3x-5y } =\frac { 7 }{ 3 } \)
⇒ 9x + 15y = 21x – 35y [By cross multiplication]
⇒ 21x – 9x = 15y + 35y

>

Question 12.
(i) If (4x² + xy) : (3xy – y²) = 12 : 5, find (x + 2y) : (2x + y).
(ii) If y (3x – y) : x (4x + y) = 5 : 12. Find (x² + y²) : (x + y)².
Solution:
(4x² + xy) : (3xy – y²) = 12 : 5
⇒ \(\frac { { 4x }^{ 2 }+xy }{ 3xy-{ y }^{ 2 } } =\frac { 12 }{ 5 } \)
⇒ 20x² + 5xy = 36xy – 12y²

Question 13.
(i) If (x – 9) : (3x + 6) is the duplicate ratio of 4 : 9, find the value of x.
(ii) If (3x + 1) : (5x + 3) is the triplicate ratio of 3 : 4, find the value of x.
(iii) If (x + 2y) : (2x – y) is equal to the duplicate ratio of 3 : 2, find x : y.
Solution:
(i) \(\frac { x-9 }{ 3x+6 } ={ \left( \frac { 4 }{ 9 } \right) }^{ 2 }\)
⇒ \(\frac { x-9 }{ 3x+6 } =\frac { 16 }{ 81 } \)

Question 14.
(i) Find two numbers in the ratio of 8 : 7 such that when each is decreased by \(12 \frac { 1 }{ 2 } \), they are in the ratio 11 : 9.
(ii) The income of a man is increased in the ratio of 10 : 11. If the increase in his income is Rs 600 per month, find his new income.
Solution:
(i) The ratio is 8 : 7
Let the numbers be 8x and 7x,
According to condition,

Question 15.
(i) A woman reduces her weight in the ratio 7 : 5. What does her weight become if originally it was 91 kg.
(ii) A school collected Rs 2100 for charity. It was decided to divide the money between an orphanage and a blind school in the ratio of 3 : 4. How much money did each receive?
Solution:
(i) Ratio between the original weight and reduced weight = 7 : 5
Let original weight = 7x
then reduced weight = 5x
If original weight = 91 kg.

Question 16.
(i) The sides of a triangle are in the ratio 7 : 5 : 3 and its perimeter is 30 cm. Find the lengths of sides.
(ii) If the angles of a triangle are in the ratio 2 : 3 : 4, find the angles.
Solution:
(i) Perimeter of a triangle = 30 cm.
Ratio among sides = 7 : 5 : 3
Sum of ratios 7 + 5 + 3 = 15

Question 17.
Three numbers are in the ratio \(\frac { 1 }{ 2 } :\frac { 1 }{ 3 } :\frac { 1 }{ 4 } \) If the sum of their squares is 244, find the numbers.
Solution:
The ratio of three numbers \(\frac { 1 }{ 2 } :\frac { 1 }{ 3 } :\frac { 1 }{ 4 } \)
= \(\frac { 6:4:3 }{ 12 } \)
= 6 : 4 : 3
Let first number 6x, second 4x and third 3x
.’. According to the condition
(6x)² + (4x)² + (3x)² = 244
⇒ 36x² + 16x² + 9x² = 244

Question 18.
(i) A certain sum was divided among A, B and C in the ratio 7 : 5 : 4. If B got Rs 500 more than C, find the total sum divided.
(ii) In a business, A invests Rs 50000 for 6 months, B Rs 60000 for 4 months and C, Rs 80000 for 5 months. If they together earn Rs 18800 find the share of each.
Solution:
(i) Ratio between A, B and C = 7 : 5 : 4
Let A’s share = 7x
B’s share = 5x
and C’s share = 4x
Total sum = 7x + 5x + 4x = 16x

Question 19.
(i) In a mixture of 45 litres, the ratio of milk to water is 13 : 2. How much water must be added to this mixture to make the ratio of milk to water as 3 : 1 ?
(ii) The ratio of the number of boys to the number of girls in a school of 560 pupils is 5 : 3. If 10 new boys are admitted, find how many new girls may be admitted so that the ratio of the number of boys to the number of girls may change to 3 : 2.
Solution:
(i) Mixture of milk and water = 45 litres
Ratio of milk and water =13 : 2
Sum of ratio = 13 + 2 = 15

Question 20.
(i) The monthly pocket money of Ravi and Sanjeev are in the ratio 5 : 7. Their expenditures are in the ratio 3 : 5. If each saves Rs 80 every month, find their monthly pocket money.
(ii) In class X of a school, the ratio of the number of boys to that of the girls is 4 : 3. If there were 20 more boys and 12 less girls, then the ratio would have been 2 : 1, How many students were there in the class?
Solution:
(i) Let the monthly pocket money of Ravi and Sanjeev be 5x and 7x respectively.
Also, let their expenditure be 3y and 5y respectively.

Question 21.
In an examination, the ratio of passes to failures was 4 : 1. If 30 less had appeared and 20 less passed, the ratio of passes to failures would have been 5 : 1. How many students appeared for the examination
Solution:
Let the number of passes = 4x
and number of failures = x
The total number of students appeared = 4x + x = 5x
In the second case, the number of students appeared = 5x – 30
and number of passes = 4x – 20

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.1 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 6 Factorization Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 6 Factorization Chapter Test

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 6 Factorization EX 6
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 6 Factorization MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 6 Factorization Chapter Test

Question 1.
Find the remainder when 2x³ – 3x² + 4x + 7 is divided by
(i) x – 2
(ii) x + 3
(iii) 2x + 1
Solution:
f(x) = 2x³ – 3x² + 4x + 7
(i) Let x – 2 = 0, then x = 2
Substituting value of x in f(x)
f(2) = 2 (2)³ – 3 (2)² + 4 (2) + 7
= 2 × 8 – 3 × 4 + 4 × 2 + 7
= 16 – 12 + 8 + 7 = 19
Remainder = 19
(ii) Let x + 3 = 0, then x = – 3
Substituting the value of x in f(x)

Question 2.
When 2x³ – 9x² + 10x – p is divided by (x + 1), the remainder is – 24.Find the value of p.
Solution:
Let x + 1 = 0 then x = -1
Substituting the value of x in f(x)
f(x) = 2x³ – 9x² + 10x – p

Question 3.
If (2x – 3) is a factor of 6x² + x + a, find the value of a. With this value of a, factorise the given expression.
Solution:
Let 2x – 3 = 0 then 2x = 3
⇒ x = \(\\ \frac { 3 }{ 2 } \)
Substituting the value of x in f(x)

Question 4.
When 3x² – 5x + p is divided by (x – 2), the remainder is 3. Find the value of p. Also factorise the polynomial 3x² – 5x + p – 3.
Solution:
f(x) = 3x² – 5x+ p
Let (x – 2) = 0, then x = 2
f(2) = 3 (2)² – 5(2) + p
= 3 x 4 – 10 + p
= 12 – 10 + p
= 2 + p

Question 5.
Prove that (5x + 4) is a factor of 5x³ + 4x² – 5x – 4. Hence factorize the given polynomial completely.
Solution:
f(x) = 5x³ + 4x² – 5x – 4
Let 5x + 4 = 0, then 5x = -4
⇒ x = \(\\ \frac { -4 }{ 2 } \)

Question 6.
Use factor theorem to factorise the following polynomials completely:
(i) 4x³ + 4x² – 9x – 9
(ii) x³ – 19x – 30
Solution:
(i) f(x) = 4x³ + 4x² – 9x – 9
Let x = -1, then
f(-1) = 4 (-1)³ + 4 (-1)² – 9 (-1) – 9

Question 7.
If x³ – 2x² + px + q has a factor (x + 2) and leaves a remainder 9, when divided by (x + 1), find the values of p and q. With these values of p and q, factorize the given polynomial completely.
Solution:
f(x) = x³ – 2x² + px + q
(x + 2) is a factor
f(-2) = (-2)³ – 2(-2)² + p (-2) + q

Question 8.
If (x + 3) and (x – 4) are factors of x³ + ax² – bx + 24, find the values of a and b: With these values of a and b, factorise the given expression.
Solution:
f(x) = x³ + ax² – bx + 24
Let x + 3 = 0, then x = -3
Substituting the value of x in f(x)

Question 9.
If 2x³ + ax² – 11x + b leaves remainder 0 and 42 when divided by (x – 2) and (x – 3) respectively, find the values of a and b. With these values of a and b, factorize the given expression.
Solution:
f(x) = 2x³ + ax² – 11 x + b
Let x – 2 = 0, then x = 2,
Substituting the vaue of x in f(x)

Question 10.
If (2x + 1) is a factor of both the expressions 2x² – 5x + p and 2x² + 5x + q, find the value of p and q. Hence find the other factors of both the polynomials.
Solution:
Let 2x + 1 = 0, then 2x = -1
x = \(– \frac { 1 }{ 2 } \)
Substituting the value of x in

Question 11.
When a polynomial f(x) is divided by (x – 1), the remainder is 5 and when it is,, divided by (x – 2), the remainder is 7. Find – the remainder when it is divided by (x – 1) (x – 2).
Solution:
When f(x) is divided by (x – 1),
Remainder = 5
Let x – 1 = 0 ⇒ x = 1

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 6 Factorization Chapter Test are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.4

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.4

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Chapter Test

Question 1.
Find the discriminant of the following equations and hence find the nature of roots:
(i) 3x² – 5x – 2 = 0
(ii) 2x² – 3x + 5 = 0
(iii) 7x² + 8x + 2 = 0
(iv) 3x² + 2x – 1 = 0
(v) 16x² – 40x + 25 = 0
(vi) 2x² + 15x + 30 = 0.
Solution:
(i) 3x² – 5x – 2 = 0
Here a = 3, b = -5, c = -2

Question 2.
Discuss the nature of the roots of the following quadratic equations :
(i) x² – 4x – 1 = 0
(ii) 3x² – 2x + \(\\ \frac { 1 }{ 3 } \) = 0
(iii) 3x² – 4√3x + 4 = 0
(iv) x² – \(\\ \frac { 1 }{ 2 } x\) + 4 = 0
(v) – 2x² + x + 1 = 0
(vi) 2√3x² – 5x + √3 = 0
Solution:
(i) x² – 4x – 1 = 0
Here a = 1, b = -4, c = -1

Question 3.
Find the nature of the roots of the following quadratic equations:
(i) x² – \(\\ \frac { 1 }{ 2 } x\) – \(\\ \frac { 1 }{ 2 } \) = 0
(ii) x² – 2√3x – 1 = 0 If real roots exist, find them.
Solution:
(i) x² – \(\\ \frac { 1 }{ 2 } x\) – \(\\ \frac { 1 }{ 2 } \) = 0
Here a = 1, b = \(– \frac { 1 }{ 2 } \), c = \(– \frac { 1 }{ 2 } \)

Question 4.
Without solving the following quadratic equation, find the value of ‘p’ for which the given equations have real and equal roots:
(i) px² – 4x + 3 = 0
(ii) x² + (p – 2)x + p = 0.
Solution:
(i) px² – 4x + 3 = 0
Here a = p, b = -4, c = 3

Question 5.
Find the value (s) of k for which each of the following quadratic equation has equal roots :
(i) kx² – 4x – 5 = 0
(ii) (k – 4) x² + 2(k – 4) x + 4 = 0
Solution:
(i) kx² – 4x – 5 = 0
Here a = k, b = -4, c = 5

Question 6.
Find the value(s) of m for which each of the following quadratic equation has real and equal roots:
(i) (3m + 1)x² + 2(m + 1)x + m = 0
(ii) x² + 2(m – 1) x + (m + 5) = 0
Solution:
(i) (3m + 1)x² + 2(m + 1)x + m = 0
Here a = 3m + 1, b = 2(m + 1), c = m

Question 7.
Find the values of k for which each of the following quadratic equation has equal roots:
(i) 9x² + kx + 1 = 0
(ii) x² – 2kx + 7k – 12 = 0
Also, find the roots for those values of k in each case.
Solution:
(i) 9x² + kx + 1 = 0
Here a = 9, b = k, c = 1

Question 8.
Find the value(s) of p for which the quadratic equation (2p + 1)x² – (7p + 2)x + (7p – 3) = 0 has equal roots. Also find these roots.
Solution:
The quadratic equation given is (2p + 1)x² – (7p + 2)x + (7p – 3) = 0
Comparing with ax² + bx + c = 0, we have

Question 9.
If – 5 is a root of the quadratic equation 2x² + px – 15 = 0 and the quadratic equation p(x² + x) + k = 0 has equal roots, find the value of k.
Solution:
-5 is a root of the quadratic equation
2x² + px – 15 = 0, then
⇒ 2(5)² – p( -5) – 15 = 0
⇒ 50 – 5p – 15 = 0
⇒ 35 – 5p = 0

Question 10.
Find the value(s) of p for which the equation 2x² + 3x + p = 0 has real roots.
Solution:
2x² + 3x + p = 0
Here, a = 2, b = 3, c = p

Question 11.
Find the least positive value of k for which the equation x² + kx + 4 = 0 has real roots.
Solution:
x² + kx + 4 = 0
Here, a = 1, b = k, c = 4

Question 12.
Find the values of p for which the equation 3x² – px + 5 = 0 has real roots.
Solution:
3x² – px + 5 = 0
Here, a = 3, b = -p, c = 5

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.4 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 6 Factorization MCQS

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 6 Factorization MCQS

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 6 Factorization EX 6
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 6 Factorization MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 6 Factorization Chapter Test

Choose the correct answer from the given four options (1 to 5) :

Question 1.
When x³ – 3x² + 5x – 7 is divided by x – 2,then the remainder is
(a) 0
(b) 1
(c) 2
(d) – 1
Solution:
f(x) = x³ – 3x² + 5x – 7
g(x) = x – 2, if x – 2 = 0, then x = 2
Remainder will be

Question 2.
When 2x³ – x² – 3x + 5 is divided by 2x + 1, then the remainder is
(a) 6
(b) – 6
(c) – 3
(d) 0
Solution:
f(x) = 2x³ – x² – 3x + 5
g(x) = 2x + 1

Question 3.
If on dividing 4x² – 3kx + 5 by x + 2, the remainder is – 3 then the value of k is
(a) 4
(b) – 4
(c) 3
(d) – 3
Solution:
f(x) = 4x² – 3kx + 5
g(x) = x + 2
Remainder = – 3
Let x + 2 = 0, then x = – 2
Now remainder will be

Question 4.
If on dividing 2x³ + 6x² – (2k – 7)x + 5 by x + 3, the remainder is k – 1 then the value of k is
(a) 2
(b) – 2
(c) – 3
(d) 3
Solution:
f(x) = 2x³ + 6x² – (2k – 7)x + 5
g(x) = x + 3
Remainder = k – 1

Question 5.
If x + 1 is a factor of 3x³ + kx² + 7x + 4, then the value of k is
(a) – 1
(b) 0
(c) 6
(d) 10
Solution:
f(x) = 3x³ + kx² + 7x + 4
g(x) = x + 1
Remainder = 0

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 6 Factorization MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Chapter Test

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Chapter Test

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Chapter Test

Question 1.
Find the compound ratio of:
(a + b)² : (a – b )² ,
(a² – b²) : (a² + b²),
(a⁴ – b⁴) : (a + b)⁴
Solution:
(a + b)² : (a – b )² ,
(a² – b²) : (a2 + b²),
(a⁴ – b⁴) : (a + b)⁴

Question 2.
If (7 p + 3 q) : (3 p – 2 q) = 43 : 2 find p : q
Solution:
(7p + 3q) : (3p – 2q) = 43 : 2
⇒ \(\frac { 7p+3q }{ 3p-2q } =\frac { 43 }{ 2 } \)

Question 3.
If a : b = 3 : 5, find (3a + 5b): (7a – 2b).
Solution:
a : b = 3 : 5
⇒ \(\frac { a }{ b } =\frac { 3 }{ 5 } \)
⇒ 3a + 5n : 7a – 2b
Dividing each term by b

Question 4.
The ratio of the shorter sides of a right angled triangle is 5 : 12. If the perimeter of the triangle is 360 cm, find the length of the longest side.
Solution:
Let the two shorter sides of a right-angled triangle be 5x and 12x.
Third (longest side)

Question 5.
The ratio of the pocket money saved by Lokesh and his sister is 5 : 6. If the sister saves Rs 30 more, how much more the brother should save in order to keep the ratio of their savings unchanged?
Solution:
Let the savings of Lokesh and his sister are 5x and 6x.
and the Lokesh should save Rs y more Now, according to the problem,
⇒ \(\frac { 5x+y }{ 6x+30 } =\frac { 5 }{ 6 } \)
⇒ 30x + 6y = 30x + 150

Question 6.
In an examination, the number of those who passed and the number of those who failed were in the ratio of 3 : 1. Had 8 more appeared, and 6 less passed, the ratio of passed to failures would have been 2 : 1. Find the number of candidates who appeared.
Solution:
Let number of passed = 3 x
and failed = x
Total candidates appeared = 3x + x = 4x.
In second case
No. of candidates appeared = 4 x + 8
and No. of passed = 3 x – 6
and failed = 4x + 8 – 3x + 6 = x + 14
then ratio will be = 2 : 1
Now according to the condition

Question 7.
What number must be added to each of the numbers 15, 17, 34 and 38 to make them proportional ?
Solution:
Let x be added to each number, then numbers will be
15 + x, 17 + x, 34 + x, and 38 + x.
Now according to the condition

Question 8.
If (a + 2 b + c), (a – c) and (a – 2 b + c) are in continued proportion, prove that b is the mean proportional between a and c.
Solution:
(a + 2 b + c), (a – c) and (a – 2 b + c) are in continued proportion
⇒ \(\frac { a+2b+c }{ a-c } =\frac { a-c }{ a-2b+c } \)

Question 9.
If 2, 6, p, 54 and q are in continued proportion, find the values of p and q.
Solution:
2, 6, p, 54 and q are in continued proportional then
⇒ \(\frac { 2 }{ 6 } =\frac { 6 }{ p } =\frac { p }{ 54 } =\frac { 54 }{ q } \)

Question 10.
If a, b, c, d, e are in continued proportion, prove that: a : e = a⁴ : b⁴.
Solution:
a, b, c, d, e are in continued proportion
⇒ \(\frac { a }{ b } =\frac { b }{ c } =\frac { c }{ d } =\frac { d }{ e } \) = k (say)

Question 11.
Find two numbers whose mean proportional is 16 and the third proportional is 128.
Solution:
Let x and y be two numbers
Their mean proportion = 16
and third proportion = 128

Question 12.
If q is the mean proportional between p and r, prove that:
\({ p }^{ 2 }-{ 3q }^{ 2 }+{ r }^{ 2 }={ q }^{ 4 }\left( \frac { 1 }{ { p }^{ 2 } } -\frac { 3 }{ { q }^{ 2 } } +\frac { 1 }{ { r }^{ 2 } } \right) \)
Solution:
q is mean proportional between p and r
q² = pr

Question 13.
If \(\frac { a }{ b } = \frac { c }{ d } = \frac { e }{ f } \), prove that each ratio is
(i) \(\sqrt { \frac { { 3a }^{ 2 }-{ 5c }^{ 2 }+{ 7e }^{ 2 } }{ { 3b }^{ 2 }-{ 5d }^{ 2 }+{ 7f }^{ 2 } } } \)
(ii) \({ \left[ \frac { { 2a }^{ 3 }+{ 5c }^{ 3 }+{ 7e }^{ 3 } }{ { 2b }^{ 3 }+{ 5d }^{ 3 }+{ 7f }^{ 3 } } \right] }^{ \frac { 1 }{ 3 } } \)
Solution:
\(\frac { a }{ b } = \frac { c }{ d } = \frac { e }{ f } \) = k(say)
∴ a = k, c = dk, e = fk

Question 14.
If \(\frac { x }{ a } = \frac { y }{ b } = \frac { z }{ c } \), prove that
\(\frac { { 3x }^{ 3 }-{ 5y }^{ 3 }+{ 4z }^{ 3 } }{ { 3a }^{ 3 }-{ 5b }^{ 3 }+{ 4c }^{ 3 } } ={ \left( \frac { 3x-5y+4z }{ 3a-5b+4c } \right) }^{ 3 }\)
Solution:
\(\frac { x }{ a } = \frac { y }{ b } = \frac { z }{ c } \) = k (say)
x = ak, y = bk, z = ck

Question 15.
If x : a = y : b, prove that
\(\frac { { x }^{ 4 }+{ a }^{ 4 } }{ { x }^{ 3 }+{ a }^{ 3 } } +\frac { { y }^{ 4 }+{ b }^{ 4 } }{ { y }^{ 3 }+{ b }^{ 3 } } =\frac { { \left( x+y \right) }^{ 4 }+{ \left( a+b \right) }^{ 4 } }{ { \left( x+y \right) }^{ 3 }+{ \left( a+b \right) }^{ 3 } } \)
Solution:
\(\frac { x }{ a } = \frac { y }{ b } \) = k (say)
x = ak, y = bk

Question 16.
If \(\frac { x }{ b+c-a } =\frac { y }{ c+a-b } =\frac { z }{ a+b-c } \) prove that each ratio’s equal to :
\(\frac { x+y+z }{ a+b+c } \)
Solution:
\(\frac { x }{ b+c-a } =\frac { y }{ c+a-b } =\frac { z }{ a+b-c } \) = k(say)
x = k(b + c – a),
y = k(c + a – b),
z = k(a + b – c)

Question 17.
If a : b = 9 : 10, find the value of
(i) \(\frac { 5a+3b }{ 5a-3b } \)
(ii) \(\frac { { 2a }^{ 2 }-{ 3b }^{ 2 } }{ { 2a }^{ 2 }+{ 3b }^{ 2 } } \)
Solution:
a : b = 9 : 10
⇒ \(\frac { a }{ b } = \frac { 9 }{ 10 }\)

Question 18.
If (3x² + 2y²) : (3x² – 2y²) = 11 : 9, find the value of \(\frac { { 3x }^{ 4 }+{ 25y }^{ 4 } }{ { 3x }^{ 4 }-{ 25y }^{ 4 } } \) ;
Solution:
\(\frac { { 3x }^{ 4 }+{ 25y }^{ 4 } }{ { 3x }^{ 4 }-{ 25y }^{ 4 } } =\frac { 11 }{ 9 } \)
Applying componendo and dividendo

Question 19.
If \(x=\frac { 2mab }{ a+b } \) , find the value of
\(\frac { x+ma }{ x-ma } +\frac { x+mb }{ x-mb } \)
Solution:
\(x=\frac { 2mab }{ a+b } \)
⇒ \(\frac { x }{ ma } +\frac { 2b }{ a+b } \)
Applying componendo and dividendo

Question 20.
If \(x=\frac { pab }{ a+b } \) ,prove that \(\frac { x+pa }{ x-pa } -\frac { x+pb }{ x-pb } =\frac { 2\left( { a }^{ 2 }-{ b }^{ 2 } \right) }{ ab } \)
Solution:
\(x=\frac { pab }{ a+b } \)
⇒ \(\frac { x }{ pa } +\frac { b }{ a+b } \)
Applying componendo and dividendo

Question 21.
Find x from the equation \(\frac { a+x+\sqrt { { a }^{ 2 }-{ x }^{ 2 } } }{ a+x-\sqrt { { a }^{ 2 }-{ x }^{ 2 } } } =\frac { b }{ x } \)
Solution:
\(\frac { a+x+\sqrt { { a }^{ 2 }-{ x }^{ 2 } } }{ a+x-\sqrt { { a }^{ 2 }-{ x }^{ 2 } } } =\frac { b }{ x } \)
Applying componendo and dividendo,

Question 22.
If \(x=\frac { \sqrt [ 3 ]{ a+1 } +\sqrt [ 3 ]{ a-1 } }{ \sqrt [ 3 ]{ a+1 } -\sqrt [ 3 ]{ a-1 } } \), prove that :
x³ – 3ax² + 3x – a = 0
Solution:
\(x=\frac { \sqrt [ 3 ]{ a+1 } +\sqrt [ 3 ]{ a-1 } }{ \sqrt [ 3 ]{ a+1 } -\sqrt [ 3 ]{ a-1 } } \)
Applying componendo and dividendo,

Question 23.
If \(\frac { by+cz }{ b^{ 2 }+{ c }^{ 2 } } =\frac { cz+ax }{ { c }^{ 2 }+{ a }^{ 2 } } =\frac { ax+by }{ { a }^{ 2 }+{ b }^{ 2 } } \), prove that each of these ratio is equal to \(\frac { x }{ a } =\frac { y }{ b } =\frac { z }{ c } \)
Solution:
\(\frac { by+cz }{ b^{ 2 }+{ c }^{ 2 } } =\frac { cz+ax }{ { c }^{ 2 }+{ a }^{ 2 } } =\frac { ax+by }{ { a }^{ 2 }+{ b }^{ 2 } } \)

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Chapter Test are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.3

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.3

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Chapter Test

Solve the following (1 to 8) equations by using formula :

Question 1.
(i) 2x² – 7x + 6 = 0
(ii) 2x² – 6x + 3 = 0
Solution:
(i) 2x² – 7x + 6 = 0
Here a = 2, b = -7, c = 6

Question 2.
(i) x² + 7x – 7 = 0
(ii) (2x + 3)(3x – 2) + 2 = 0
Solution:
(i) x² + 7x – 7 = 0
Here a = 1, b = 7, c = -7

Question 3.
(i)256x² – 32x + 1 = 0
(ii) 25x² + 30x + 7 = 0
Solution:
(i) 256x² – 32x + 1 = 0
Here a = 256, b = -32, c = 1

Question 4.
(i) 2x² + √5x – 5 = 0
(ii) √3x² + 10x – 8√3 = 0
Solution:
(i) 2x² + √5x – 5 = 0
Here a = 2, b = √5, c = -5

Question 5.
(i) \(\frac { x-2 }{ x+2 } +\frac { x+2 }{ x-2 } =4\)
(ii) \(\frac { x+1 }{ x+3 } =\frac { 3x+2 }{ 2x+3 } \)
Solution:
(i) \(\frac { x-2 }{ x+2 } +\frac { x+2 }{ x-2 } =4\)
⇒ \(\frac { { (x-2) }^{ 2 }+{ (x+2) }^{ 2 } }{ (x+2)(x-2) } =4\)

Question 6.
(i) a (x² + 1) = (a² + 1) x , a ≠ 0
(ii) 4x² – 4ax + (a² – b²) = 0
Solution:
(i) a (x² + 1) = (a² + 1) x
ax² – (a² + 1)x + a = 0

Question 7.
(i)\(x-\frac { 1 }{ x } =3,x\neq 0\)
(ii)\(\frac { 1 }{ x } +\frac { 1 }{ x-2 } =3,x\neq 0,2\)
Solution:
(i)\(x-\frac { 1 }{ x } =3\)
x² – 1 = 3x
⇒ x² – 3x – 1 = 0

Question 8.
\(\frac { 1 }{ x-2 } +\frac { 1 }{ x-3 } +\frac { 1 }{ x-4 } =0\)
Solution:
\(\frac { 1 }{ x-2 } +\frac { 1 }{ x-3 } +\frac { 1 }{ x-4 } =0\)
⇒ \(\frac { 1 }{ x-2 } +\frac { 1 }{ x-3 } =-\frac { 1 }{ x-4 } \)

Question 9.
Solve for \(x:2\left( \frac { 2x-1 }{ x+3 } \right) -3\left( \frac { x+3 }{ 2x-1 } \right) =5,x\neq -3,\frac { 1 }{ 2 } \)
Solution:
\(x:2\left( \frac { 2x-1 }{ x+3 } \right) -3\left( \frac { x+3 }{ 2x-1 } \right) =5 \)
Let \(\frac { 2x-1 }{ x+3 } =y\) then \(\frac { x+3 }{ 2x-1 } =\frac { 1 }{ y } \)

Question 10.
Solve the following equation by using quadratic equations for x and give your
(i) x² – 5x – 10 = 0
(ii) 5x(x + 2) = 3
Solution:
(i) x² – 5x – 10 = 0
On comparing with, ax² + bx + c = 0

Question 11.
Solve the following equations by using quadratic formula and give your answer correct to 2 decimal places :
(i) 4x² – 5x – 3 = 0
(ii) 2x – \(\\ \frac { 1 }{ x } \) = 1
Solution:
(i) Given equation 4x² – 5x – 3 = 0
Comparing with ax² + bx + c = 0, we have

Question 12.
Solve the following equation: \(x-\frac { 18 }{ x } =6\). Give your answer correct to two x significant figures. (2011)
Solution:
\(x-\frac { 18 }{ x } =6\)
⇒ x² – 6x – 18 = 0
a = 1, b = -6, c = -18

Question 13.
Solve the equation 5x² – 3x – 4 = 0 and give your answer correct to 3 significant figures:
Solution:
We have 5x² – 3x – 4 = 0
Here a = 5, b = – 3, c = – 4

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion MCQS

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion MCQS

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Chapter Test

Choose the correct answer from the given options (1 to 10):

Question 1.
The ratio of 45 minutes to \(5 \frac { 3 }{ 4 } \) hours is
(a) 180:23
(b) 3:23
(c) 23:3
(d) 6:23
Solution:
ratio of 45 minutes to \(5 \frac { 3 }{ 4 } \) hours is
45 minutes to : \(5 \frac { 3 }{ 4 } \) hours

Question 2.
The ratio of 4 litres to 900 mL is
(a) 4 : 9
(b) 40 : 9
(c) 9 : 40
(d) 20 : 9
Solution:
4l : 900 ml
= 4000 ml : 900 ml
= 4000 : 900
= 40 : 9 (b)

Question 3.
When the number 210 is increased in the ratio 5 : 7, the the new number is
(a) 150
(b) 180
(c) 294
(d) 420
Solution:
210 is increased in the ratio 5 : 7, then
New increased number will be
= 210 × \(\\ \frac { 7 }{ 5 } \)
= 294 (c)

Question 4.
Two numbers are in the ratio 7 : 9. If the sum of the numbers is 288, then the smaller number is
(a) 126
(b) 162
(c) 112
(d) 144
Solution:
Ratio in two number = 7 : 9
Sum of numbers = 288
Sum of ratios = 7 + 9
= 16
Smaller number = \(\\ \frac { 288\times 7 }{ 16 } \)
= 126 (a)

Question 5.
A ratio equivalent to the ratio \(\\ \frac { 2 }{ 3 } \) : \(\\ \frac { 5 }{ 7 } \) is
(a) 4:6
(b) 5:7
(c) 15:14
(d) 14:15
Solution:
\(\\ \frac { 2 }{ 3 } \) : \(\\ \frac { 5 }{ 7 } \)
Multiply and divide \(\\ \frac { 2 }{ 3 } \) by 7 and
Multiply and divide \(\\ \frac { 5 }{ 7 } \) by 3

Question 6.
The ratio of number of edges of a cube to the number of its faces is
(a) 2 : 1
(b) 1 : 2
(c) 3 : 8
(d) 8 : 3
Solution:
No. of edges of the cube = 12
No. of faces = 6
Ratio in edges a cube to the number of faces = 12 : 6
= 2 : 1 (a)

Question 7.
If x, 12, 8 and 32 are in proportion, then the value of x is
(a) 6
(b) 4
(c) 3
(d) 2
Solution:
x, 12, 8, 32 are in proportion, then
x × 32 = 12 × 8 (∵ ad = bc)
⇒ x = \(\\ \frac { 12\times 8 }{ 32 } \) = 3
x = 3 (c)

Question 8.
The fourth proportional to 3, 4, 5 is
(a) 6
(b) \(\\ \frac { 20 }{ 3 } \)
(c) \(\\ \frac { 15 }{ 4 } \)
(d) \(\\ \frac { 12 }{ 5 } \)
Solution:
The fourth proportion to 3, 4, 5 will be
= \(\\ \frac { 4\times 5 }{ 3 } \)
= \(\\ \frac { 20 }{ 3 } \) (b)

Question 9.
The third proportional to \(6 \frac { 1 }{ 4 } \) and 5 is
(a) 4
(b) \(8 \frac { 1 }{ 2 } \)
(c) 3
(d) none of these
Solution:
The third proportional to \(6 \frac { 1 }{ 4 } \) and 5 is
⇒ \(6 \frac { 1 }{ 4 } \) : 5 :: 5 : x
⇒ \(\\ \frac { 25 }{ 4 } \) : 5 :: 5 : x
⇒ x = \(\\ \frac { 5\times 5 }{ 25 } \) × 4
⇒ 4 (a)

Question 10.
The mean proportional between \(\\ \frac { 1 }{ 2 } \) and 128 is
(a) 64
(b) 32
(c) 16
(d) 8
Solution:
The mean proportional between \(\\ \frac { 1 }{ 2 } \) and 128 is
= \(\sqrt { \frac { 1 }{ 2 } \times 128 } \)
= √64
= 8 (d)

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion MCQS are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 6 Factorization Ex 6

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 6 Factorization Ex 6

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 6 Factorization EX 6
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 6 Factorization MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 6 Factorization Chapter Test

Question 1.
Find the remainder (without divisions) on dividing f(x) by x – 2, where
(i) f(x) = 5x² – 1x + 4
(ii) f (x) = 2x³ – 7x² + 3
Solution:
Let x – 2 = 0, then x = 2
(i) Substituting value of x in f(x)
f(x) = 5x² – 7x + 4
⇒ f(2) = 5(2)² – 7(2) + 4

Question 2.
Using remainder theorem, find the remainder on dividing f(x) by (x + 3) where
(i) f(x) = 2x² – 5x + 1
(ii) f(x) = 3x³ + 7x² – 5x + 1
Solution:
Let x + 3 = 0
⇒ x = -3
Substituting the value of x in f(x),

Question 3.
Find the remainder (without division) on dividing f(x) by (2x + 1) where
(i) f(x) = 4x² + 5x + 3
(ii) f(x) = 3x³ – 7x² + 4x + 11
Solution:
Let 2x + 1 = 0, then x = \(– \frac { 1 }{ 2 } \)
Substituting the value of x in f(x):
(i) f(x) = 4x² + 5x + 3

Question 4.
(i) Find the remainder (without division) when 2x³ – 3x² + 7x – 8 is divided by x – 1 (2000)
(ii) Find the remainder (without division) on dividing 3x² + 5x – 9 by (3x + 2)
Solution:
(i) Let x – 1 = 0, then x = 1
Substituting value of x in f(x)

Question 5.
Using remainder theorem, find the value of k if on dividing 2x³ + 3x² – kx + 5 by x – 2, leaves a remainder 7. (2016)
Solution:
f(x) = 2x² + 3x² – kx + 5
g(x) = x – 2, if x – 2 = 0, then x = 2
Dividing f(x) by g(x) the remainder will be

Question 6.
Using remainder theorem, find the value of a if the division of x³ + 5x² – ax + 6 by (x – 1) leaves the remainder 2a.
Solution:
Let x – 1 = 0, then x = 1
Substituting the value of x in f(x)

Question 7.
(i) What number must be subtracted from 2x² – 5x so that the resulting polynomial leaves the remainder 2, when divided by 2x + 1 ?
(ii) What number must be added to 2x³ – 7x² + 2x so that the resulting polynomial leaves the remainder – 2 when divided by 2x – 3?
Solution:
(i) Let a be subtracted from 2x² – 5x,
Dividing 2x² – 5x by 2x + 1,

Question 8.
(i) When divided by x – 3 the polynomials x² – px² + x + 6 and 2x³ – x² – (p + 3) x – 6 leave the same remainder. Find the value of ‘p’
(ii) Find ‘a’ if the two polynomials ax³ + 3x² – 9 and 2x³ + 4x + a, leaves the same remainder when divided by x + 3.
Solution:
By dividing
x³ – px² + x + 6
and 2x³ – x² – (p + 3) x – 6

Question 9.
By factor theorem, show that (x + 3) and (2x – 1) are factors of 2x² + 5x – 3.
Solution:
Let x + 3 = 0 then x = – 3
Substituting the value of x in f(x)

Question 10.
Show that (x – 2) is a factor of 3x² – x – 10 Hence factorise 3x² – x – 10.
Solution:
Let x – 2 = 0, then x = 2
Substituting the value of x in f(x),

Question 11.
Show that (x – 1) is a factor of x³ – 5x² – x + 5 Hence factorise x³ – 5x² – x + 5.
Solution:
Let x – 1 = 0, then x = 1
Substituting the value of x in f(x),

Question 12.
Show that (x – 3) is a factor of x³ – 7x² + 15x – 9. Hence factorise x³ – 7x² + 15 x – 9
Solution:
Let x – 3 = 0, then x = 3,
Substituting the value of x in f(x),

Question 13.
Show that (2x + 1) is a factor of 4x³ + 12x² + 11 x + 3 .Hence factorise 4x³ + 12x² + 11x + 3.
Solution:
Let 2x + 1 = 0,
then x = \(– \frac { 1 }{ 2 } \)
Substituting the value of x in f(x),

Question 14.
Show that 2x + 7 is a factor of 2x³ + 5x² – 11x – 14. Hence factorise the given expression completely, using the factor theorem. (2006)
Solution:
Let 2x + 7 = 0, then 2x = -7
x = \(\\ \frac { -7 }{ 2 } \)
substituting the value of x in f(x),

Question 15.
Use factor theorem to factorise the following polynominals completely.
(i) x³ + 2x² – 5x – 6
(ii) x³ – 13x – 12.
Solution:
(i) Let f(x) = x³ + 2x² – 5x – 6

Question 16.
(i) Use the Remainder Theorem to factorise the following expression : 2x³ + x² – 13x + 6. (2010)
(ii) Using the Remainder Theorem, factorise completely the following polynomial: 3x² + 2x² – 19x + 6 (2012)
Solution:
(i) Let f(x) = 2x³ + x² – 13x + 6
Factors of 6 are ±1, ±2, ±3, ±6
Let x = 2, then

Question 17.
Using the Remainder and Factor Theorem, factorise the following polynomial: x³ + 10x² – 37x + 26.
Solution:
f(x) = x³ + 10x² – 37x + 26
f(1) = (1)³ + 10(1)² – 37(1) + 26
= 1 + 10 – 37 + 26 = 0
x = 1

Question 18.
If (2 x + 1) is a factor of 6x³ + 5x² + ax – 2 find the value of a
Solution:
Let 2x + 1 = 0, then x = \(– \frac { 1 }{ 2 } \)
Substituting the value of x in f(x),
f(x) = 6x³ + 5x² + ax – 2

Question 19.
If (3x – 2) is a factor of 3x³ – kx² + 21x – 10, find the value of k.
Solution:
Let 3x – 2 = 0, then 3x = 2
⇒ x = \(\\ \frac { 2 }{ 3 } \)
Substituting the value of x in f(x),
f(x) = 3x³ – kx² + 21x – 10

Question 20.
If (x – 2) is a factor of 2x³ – x² + px – 2, then
(i) find the value of p.
(ii) with this value of p, factorise the above expression completely
Solution:
(i) Let x – 2 = 0, then x = 2
Now f(x) = 2x³ – x² + px – 2

Question 21.
Find the value of ‘K’ for which x = 3 is a solution of the quadratic equation, (K + 2)x² – Kx + 6 = 0.
Also, find the other root of the equation.
Solution:
(K + 2)x² – Kx + 6 = 0 …(1)
Substitute x = 3 in equation (1)

Question 22.
What number should be subtracted from 2x³ – 5x² + 5x so that the resulting polynomial has 2x – 3 as a factor?
Solution:
Let the number to be subtracted be k and the resulting polynomial be f(x), then
f(x) = 2x³ – 5x² + 5x – k
Since, 2x – 3 is a factor of f(x),
Now, converting 2x – 3 to factor theorem

Question 23.
Find the value of the constants a and b, if (x – 2) and (x + 3) are both factors of the expression x³ + ax² + bx – 12.
Solution:
Let x – 2 = 0, then x = 0
Substituting value of x in f(x)
f(x) = x³ + ax² + bx – 12

Question 24.
If (x + 2) and (x – 3) are factors of x³ + ax + b, find the values of a and b. With these values of a and b, factorise the given expression.
Solution:
Let x + 2 = 0, then x = -2
Substituting the value of x in f(x),
f(x) = x³ + ax + b

Question 25.
(x – 2) is a factor of the expression x³ + ax² + bx + 6. When this expression is divided by (x – 3), it leaves the remainder 3. Find the values of a and b. (2005)
Solution:
As x – 2 is a factor of
f(x) = x³ + ax² + bx + 6

Question 26.
If (x – 2) is a factor of the expression 2x³ + ax² + bx – 14 and when the expression is divided by (x – 3), it leaves a remainder 52, find the values of a and b.
Solution:
f(x) = 2x³ + ax² + bx – 14
∴ (x – 2) is factor of f(x)
f(2) = 0

Question 27.
If ax³ + 3x² + bx – 3 has a factor (2x + 3) and leaves remainder – 3 when divided by (x + 2), find the values of a and 6. With these values of a and 6, factorise the given expression.
Solution:
Let 2x + 3 = 0 then 2x = -3
⇒ x = \(\\ \frac { -3 }{ 2 } \)
Substituting the value of x in f(x),
f(x) = ax³ + 3x² + 6x – 3

Question 28.
Given f(x) = ax² + bx + 2 and g(x) = bx² + ax + 1. If x – 2 is a factor of f(x) but leaves the remainder – 15 when it divides g(x), find the values of a and b. With these values of a and b, factorise the expression. f(x) + g(x) + 4x² + 7x.
Solution:
f(x) = ax² + bx + 2
g(x) = bx² + ax + 1
x – 2 is a factor of f(x)
Let x – 2 = 0
⇒ x = 2

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 6 Factorization Ex 6 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.2

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.2

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.4
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.5
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Chapter Test

Solve the following equations (1 to 24) by factorization

Question 1.
(i) 4x² = 3x
(ii) \(\frac { { x }^{ 2 }-5x }{ 2 } =0\)
Solution:
(i) 4x² = 3x
x(4x – 3) = 0
Either x = 0,

Question 2.
(i) (x – 3) (2x + 5) = 0
(ii) x (2x + 1) = 6
Solution:
(i) (x – 3) (2x + 5) = 0
Either x – 3 = 0,
Then x = 3

Question 3.
(i) x² – 3x – 10 = 0
(ii) x(2x + 5) = 3
Solution:
(i) x² – 3x – 10 = 0
⇒ x² – 5x + 2x – 10 = 0
⇒ x(x – 5) + 2(x – 5) = 0

Question 4.
(i) 3x² – 5x – 12 = 0
(ii) 21x² – 8x – 4 = 0
Solution:
(i) 3x² – 5x – 12 = 0
⇒ 3x² – 9x + 4x – 12 = 0
⇒ 3x (x – 3) + 4(x – 3) = 0

Question 5.
(i) 3x² = x + 4
(ii) x(6x – 1) = 35
Solution:
(i) 3x² = x + 4
⇒ 3x² – x – 4 = 0
⇒ 3x² – 4x + 3x – 4 = 0

Question 6.
(i) 6p² + 11p – 10 = 0
(ii) \(\frac { 2 }{ 3 } { x }^{ 2 }-\frac { 1 }{ 3 } x=1 \)
Solution:
(i) 6p² + 11p – 10 = 0
⇒ 6p² + 15p – 4p – 10 = 0
⇒ 3p(2p + 5) – 2(2p + 5) = 0

Question 7.
(i) (x – 4)² + 5² = 13²
(ii) 3(x – 2)² = 147
Solution:
(i) (x – 4)² + 5² = 13²
x² – 8x + 16 + 25 = 169

Question 8.
(i) \(\\ \frac { 1 }{ 7 } \)(3x – 5)² = 28
(ii) 3(y² – 6) = y(y + 7) – 3
Solution:
(i) \(\\ \frac { 1 }{ 7 } \)(3x – 5)² = 28
(3x – 5)² = 28 × 7
⇒ 9x² – 30x + 25 = 196

Question 9.
x² – 4x – 12 = 0,when x∈N
Solution:
x² – 4x – 12 = 0
⇒ x² – 6x + 2x – 12 = 0
⇒ x (x – 6) + 2 (x – 6) = 0
⇒ (x – 6) (x + 2) = 0
Either x – 6 = 0, then x = 6
or x + 2 = 0, then x = -2
But -2 is not a natural number
∴ x = 6

Question 10.
2x² – 8x – 24 = 0 when x∈I
Solution:
2x² – 8x – 24 = 0
⇒ x² – 4x – 12 = 0 (Dividing by 2)
⇒ x² – 6x + 2x – 12 = 0
⇒ x (x – 6) + 2 (x – 6) = 0
⇒ (x – 6) (x + 2) = 0
Either x – 6 = 0, then, x = 6
or x + 2 = 0, then x = – 2
Hence x = 6, – 2

Question 11.
5x² – 8x – 4 = 0 when x∈Q
Solution:
5x² – 8x – 4 = 0
∵ 5 × ( – 4) = – 20
-20 = – 10 + 2
-8 = – 10 + 2

Question 12.
2x² – 9x + 10 = 0,when
(i)x∈N
(ii)x∈Q
Solution:
2x² – 9x + 10 = 0
⇒ 2x² – 4x – 5x + 10 = 0
⇒ 2x(x – 2) – 5(x – 2) = 0

Question 13.
(i) a²x² + 2ax + 1 = 0, a≠0
(ii) x² – (p + q)x + pq = 0
Solution:
(i) a²x² + 2ax + 1 = 0
⇒ a²x² + ax + ax + 1 = 0

Question 14.
a²x² + (a² + b²)x + b² = 0, a≠0
Solution:
a²x² + (a² + b²)x + b² = 0
⇒ a²x(x + 1) + b²(x + 1) = 0

Question 15.
(i) √3x² + 10x + 7√3 = 0
(ii) 4√3x² + 5x – 2√3 = 0
Solution:
(i) √3x² + 10x + 7√3 = 0
[ ∵ √3 x 7√3 = 7 x 3 = 21]
⇒ √3x(x + √3) + 7(x + √3) = 0

Question 16.
(i) x² – (1 + √2)x + √2 = 0
(ii) \(x+ \frac { 1 }{ x } \) = \(2 \frac { 1 }{ 20 } \)
Solution:
(i) x² – (1 + √2)x + √2 = 0
⇒ x² – x – √2x + √2 = 0

Question 17.
(i) \(\frac { 2 }{ { x }^{ 2 } } -\frac { 5 }{ x } +2=0,x\neq 0 \)
(ii)\(\frac { { x }^{ 2 } }{ 15 } -\frac { x }{ 3 } -10=0 \)
Solution:
(i) \(\frac { 2 }{ { x }^{ 2 } } -\frac { 5 }{ x } +2=0,x\neq 0 \)
⇒ 2 – 5x + 2x² = 0

Question 18.
(i) \(3x-\frac { 8 }{ x } =2 \)
(ii) \(\frac { x+2 }{ x+3 } =\frac { 2x-3 }{ 3x-7 } \)
Solution:
(i) \(3x-\frac { 8 }{ x } =2 \)
\(\frac { { 3x }^{ 2 }-8 }{ x } =2 \)

Question 19.
(i) \(\frac { 8 }{ x+3 } -\frac { 3 }{ 2-x } =2 \)
(ii) \(\frac { x }{ x-1 } +\frac { x-1 }{ x } =2\frac { 1 }{ 2 } \)
Solution:
(i) \(\frac { 8 }{ x+3 } -\frac { 3 }{ 2-x } =2 \)
\(\frac { 16-8x-3x-9 }{ (x+3)(2-x) } =2 \)

Question 20.
(i) \(\frac { x }{ x+1 } +\frac { x+1 }{ x } =\frac { 34 }{ 15 } \)
(ii) \(\frac { x+1 }{ x-1 } +\frac { x-2 }{ x+2 } =3 \)
Solution:
(i) \(\frac { x }{ x+1 } +\frac { x+1 }{ x } =\frac { 34 }{ 15 } \)
\(\frac { { x }^{ 2 }+{ x }^{ 2 }+2x+1 }{ x(x+1) } =\frac { 34 }{ 15 } \)

Question 21.
(i) \(\frac { 1 }{ x-3 } -\frac { 1 }{ x+5 } =\frac { 1 }{ 6 } \)
(ii) \(\frac { x-3 }{ x+3 } +\frac { x+3 }{ x-3 } =2\frac { 1 }{ 2 } \)
Solution:
(i) \(\frac { 1 }{ x-3 } -\frac { 1 }{ x+5 } =\frac { 1 }{ 6 } \)

Question 22.
(i) \(\frac { a }{ ax-1 } +\frac { b }{ bx-1 } =a+b,a+b\neq 0,ab\neq 0\)
(ii) \(\frac { 1 }{ 2a+b+2x } =\frac { 1 }{ 2a } +\frac { 1 }{ b } +\frac { 1 }{ 2x } \)
Solution:
(i) \(\frac { a }{ ax-1 } +\frac { b }{ bx-1 } =a+b\)
⇒ \(\left( \frac { a }{ ax-1 } -b \right) +\left( \frac { b }{ bx-1 } -a \right) =0\)

Question 23.
\(\frac { 1 }{ x+6 } +\frac { 1 }{ x-10 } =\frac { 3 }{ x-4 } \)
Solution:
\(\frac { 1 }{ x+6 } +\frac { 1 }{ x-10 } =\frac { 3 }{ x-4 } \)
⇒ \(\frac { x-10+x+6 }{ (x+6)(x-10) } =\frac { 3 }{ x-4 } \)

Question 24.
(i) \(\sqrt { 3x+4 } =x\)
(ii) \(\sqrt { x(x-7) } =3\sqrt { 2 } \)
Solution:
(i) \(\sqrt { 3x+4 } =x\)
Squaring on both sides

Question 25.
Use the substitution y = 3x + 1 to solve for x : 5(3x + 1 )² + 6(3x + 1) – 8 = 0
Solution:
y = 3x + 1
Now, 5(3x + 1)² + 6(3x + 1) – 8 = 0

Question 26.
Find the values of x if p + 1 =0 and x² + px – 6 = 0
Solution:
p + 1 = 0, then p = – 1
Substituting the value of p in the given quadratic equation
x² + ( – 1)x – 6 = 0
⇒ x² – x – 6 = 0
⇒ x² – 3x + 2x – 6 = 0
⇒ x (x – 3) + 2 (x – 3) = 0
⇒ (x – 3) (x + 2) = 0
Either x – 3 = 0, then x = 3
or x + 2 = 0, then x = – 2
Hence x = 3, -2

Question 27.
Find the values of x if p + 7 = 0, q – 12 = 0 and x² + px + q = 0,
Solution:
p + 7 = 0, then p = – 7
and q – 12 = 0, then q = 12
Substituting the values of p and q in the given quadratic equation,
x² – 7x + 12 = 0
⇒ x² – 3x – 4x + 12 = 0
⇒ x (x – 3) – 4 (x – 3) = 0
⇒ (x – 3) (x – 4) = 0
Either x – 3 = 0, then x = 3
or x – 4 = 0, then x = 4
Hence x = 3, 4

Question 28.
If x = p is a solution of the equation x(2x + 5) = 3, then find the value of p.
Solution:
Given, x = p and x(2x + 5) = 3
Substituting the value of p, we get
p(2p + 5) = 3
⇒ 2p² + 5p – 3 = 0
⇒ 2p² + 6p – p – 3 = 0

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 5 Quadratic Equations in One Variable Ex 5.2 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.3

These Solutions are part of ML Aggarwal Class 10 Solutions for ICSE Maths. Here we have given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.3

More Exercises

• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.1
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.2
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.3
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion MCQS
• ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Chapter Test

Question 1.
If a : b : : c : d, prove that
(i) \(\frac { 2a+5b }{ 2a-5b } =\frac { 2c+5d }{ 2c-5d } \)
(ii) \(\frac { 5a+11b }{ 5c+11d } =\frac { 5a-11b }{ 5c-11d } \)
(iii) (2a + 3b)(2c – 3d) = (2a – 3b)(2c + 3d)
(iv) (la + mb) : (lc + mb) :: (la – mb) : (lc – mb)
Solution:
(i) a : b : : c : d
then \(\frac { a }{ b } =\frac { c }{ d } \)
⇒ \(\frac { 2a }{ 5b } =\frac { 2c }{ 5d } \) (multiply by \(\\ \frac { 2 }{ 5 } \) )

Question 2.
(i) If \(\frac { 5x+7y }{ 5u+7v } =\frac { 5x-7y }{ 5u-7v } \) , Show that \(\frac { x }{ y } =\frac { u }{ v } \)
(ii) \(\frac { 8a-5b }{ 8c-5d } =\frac { 8a+5b }{ 8c+5d } \) , prove that \(\frac { a }{ b } =\frac { c }{ d } \)
Solution:
(i) \(\frac { 5x+7y }{ 5u+7v } =\frac { 5x-7y }{ 5u-7v } \)
Applying alternendo \(\frac { 5x+7y }{ 5u+7v } =\frac { 5x-7y }{ 5u-7v } \)
Applying componendo and dividendo

Question 3.
If (4a + 5b) (4c – 5d) = (4a – 5d) (4c + 5d), prove that a, b, c, d are in proporton.
Solution:
(4a + 5b) (4c – 5d) = (4a – 5d) (4c + 5d)
⇒ \(\frac { 4a+5b }{ 4a-5b } =\frac { 4c+5d }{ 4c-5d } \)
Applying componendo and dividendo

Question 4.
If (pa + qb) : (pc + qd) :: (pa – qb) : (pc – qd) prove that a : b : : c : d
Solution:
(pa + qb) : (pc + qd) :: (pa – qb) : (pc – qd)
⇒ \(\frac { pa+qb }{ pc+qd } =\frac { pq-qb }{ pc-qd } \)
⇒ \(\frac { pa+qb }{ pc-qd } =\frac { pq+qb }{ pc-qd } \)
Applying componendo and dividendo
⇒ \(\frac { pa+qb+pa-qb }{ pa+qb-pa+qb } =\frac { pc+qd+pc-qd }{ pc-qd-pc+qd } \)

Question 5.
If (ma + nb): b :: (mc + nd) : d, prove that a, b, c, d are in proportion.
Solution:
(ma + nb): b :: (mc + nd) : d
⇒ \(\frac { ma+nb }{ b } =\frac { mc+nd }{ d } \)
⇒ mad + nbd = mbc + nbd
⇒ mad = mbc
⇒ ad = bc
⇒ \(\frac { a }{ b } =\frac { c }{ d } \)
Hence a : b :: c : d.

Question 6.
If (11a² + 13b²) (11c² – 13d²) = (11a² – 13b²)(11c² + 13d²), prove that a : b :: c : d.
Solution:
(11a² + 13b²) (11c² – 13d²) = (11a² – 13b²)(11c² + 13d²)
⇒ \(\frac { 11a+{ 13b }^{ 2 } }{ { 11a }^{ 2 }-{ 13b }^{ 2 } } =\frac { { 11c }^{ 2 }+{ 13d }^{ 2 } }{ { 11c }^{ 2 }-{ 13d }^{ 2 } } \)
Applying componendo and dividendo

Question 7.
If (a + 3b + 2c + 6d) (a – 3b – 2c + 6d) = (a + 3b – 2c – 6d) (a – 3b + 2c – 6d), prove that a : b :: c : d.
Solution:
\(\frac { a + 3b + 2c + 6d }{ a – 3b + 2c – 6d } =\frac { a + 3b – 2c – 6d }{ a – 3b – 2c + 6d } \)
⇒ \(\frac { a + 3b + 2c + 6d }{ a + 3b – 2c – 6d } =\frac { a – 3b + 2c – 6d }{ a – 3b – 2c + 6d } \) (by altenendo)
Applying componendo and dividendo

Question 8.
If \(x=\frac { 2ab }{ a+b } \) find the value of \(\frac { x+a }{ x-a } +\frac { x+b }{ x-b } \)
Solution:
\(x=\frac { 2ab }{ a+b } \)
⇒ \(\frac { x }{ a } =\frac { 2b }{ a+b } \)
Applying componendo and dividendo,

Question 9.
If \(x=\frac { 8ab }{ a+b } \) find the value of \(\frac { x+4a }{ x-4a } +\frac { x+4b }{ x-4b } \)
Solution:
\(x=\frac { 8ab }{ a+b } \)
⇒ \(\frac { x }{ 4a } =\frac { 2b }{ a+b } \)
Applying componendo and dividendo,

Question 10.
If \(x=\frac { 4\sqrt { 6 } }{ \sqrt { 2 } +\sqrt { 3 } } \) find the value of \(\frac { x+2\sqrt { 2 } }{ x-2\sqrt { 2 } } +\frac { x+2\sqrt { 3 } }{ x-2\sqrt { 3 } } \)
Solution:
\(x=\frac { 4\sqrt { 6 } }{ \sqrt { 2 } +\sqrt { 3 } } \)
⇒ \(\frac { 4\sqrt { 2 } \times \sqrt { 3 } }{ \sqrt { 2 } +\sqrt { 3 } } \)

Question 11.
Solve \(x:\frac { \sqrt { 36x+1 } +6\sqrt { x } }{ \sqrt { 36x+1 } -6\sqrt { x } } =9 \)
Solution:
\(\frac { \sqrt { 36x+1 } +6\sqrt { x } }{ \sqrt { 36x+1 } -6\sqrt { x } } =\frac { 9 }{ 1 } \)
Applying componendo and dividendo,

Question 12.
Find x from the following equations :
(i) \(\frac { \sqrt { 2-x } +\sqrt { 2+x } }{ \sqrt { 2-x } -\sqrt { 2+x } } =3 \)
(ii) \(\frac { \sqrt { x+4 } +\sqrt { x-10 } }{ \sqrt { x+4 } -\sqrt { x-10 } } =\frac { 5 }{ 2 } \)
(iii) \(\frac { \sqrt { 1+x } +\sqrt { 1-x } }{ \sqrt { 1+x } -\sqrt { 1-x } } =\frac { a }{ b } \)
(iv) \(\frac { \sqrt { 12x+1 } +\sqrt { 2x-3 } }{ \sqrt { 12x+1 } -\sqrt { 2x-3 } } =\frac { 3 }{ 2 } \)
(v) \(\frac { 3x+\sqrt { { 9x }^{ 2 }-5 } }{ 3x-\sqrt { { 9x }^{ 2 }-5 } } =5 \)
(vi) \(\frac { \sqrt { a+x } +\sqrt { a-x } }{ \sqrt { a+x } -\sqrt { a-x } } =\frac { c }{ d } \)
Solution:
(i) \(\frac { \sqrt { 2-x } +\sqrt { 2+x } }{ \sqrt { 2-x } -\sqrt { 2+x } } =3 \)
Applying componendo and dividendo,

Question 13.
Solve \(\frac { 1+x+{ x }^{ 2 } }{ 1-x+{ x }^{ 2 } } =\frac { 62\left( 1+x \right) }{ 63\left( 1-x \right) } \)
Solution:
\(\frac { 1+x+{ x }^{ 2 } }{ 1-x+{ x }^{ 2 } } =\frac { 62\left( 1+x \right) }{ 63\left( 1-x \right) } \)
⇒ \(\frac { \left( 1-x \right) \left( 1+x+{ x }^{ 2 } \right) }{ \left( 1+x \right) \left( 1-x+{ x }^{ 2 } \right) } =\frac { 62 }{ 63 } \)
⇒ \(\frac { \left( 1+x \right) \left( 1-x+{ x }^{ 2 } \right) }{ \left( 1-x \right) \left( 1+x+{ x }^{ 2 } \right) } =\frac { 63 }{ 62 } \)

Question 14.
Solve for \(x:16{ \left( \frac { a-x }{ a+x } \right) }^{ 3 }=\frac { a+x }{ a-x } \)
Solution:
\(x:16{ \left( \frac { a-x }{ a+x } \right) }^{ 3 }=\frac { a+x }{ a-x } \)
⇒ \(\left( \frac { a+x }{ a-x } \right) \times { \left( \frac { a+x }{ a-x } \right) }^{ 3 }=16 \)

Question 15.
If \(x=\frac { \sqrt { a+x } +\sqrt { a-1 } }{ \sqrt { a+1 } -\sqrt { a-1 } } \) , using properties of proportion , show that x² – 2ax + 1 = 0
Solution:
We have \(x=\frac { \sqrt { a+x } +\sqrt { a-1 } }{ \sqrt { a+1 } -\sqrt { a-1 } } \)
⇒ \(\frac { x+1 }{ x-1 } =\frac { 2\sqrt { a+1 } }{ 2\sqrt { a-1 } } \)

Question 16.
Given \(x=\frac { \sqrt { { a }^{ 2 }+{ b }^{ 2 } } +\sqrt { { a }^{ 2 }-{ b }^{ 2 } } }{ \sqrt { { a }^{ 2 }+{ b }^{ 2 } } -\sqrt { { a }^{ 2 }-{ b }^{ 2 } } } \) Use componendo and dividendo to prove that \({ b }^{ 2 }=\frac { { 2a }^{ 2 }x }{ { x }^{ 2 }+1 } \)
Solution:
If \(\frac { x }{ 1 } =\frac { \sqrt { { a }^{ 2 }+{ b }^{ 2 } } +\sqrt { { a }^{ 2 }-{ b }^{ 2 } } }{ \sqrt { { a }^{ 2 }+{ b }^{ 2 } } -\sqrt { { a }^{ 2 }-{ b }^{ 2 } } } \)
Applying componendo and dividendo both sides

Question 17.
Given that \(\frac { { a }^{ 3 }+3{ ab }^{ 2 } }{ { b }^{ 3 }+{ 3a }^{ 2 }b } =\frac { 63 }{ 62 } \). Using componendo and dividendo find a: b. (2009)
Solution:
Given that \(\frac { { a }^{ 3 }+3{ ab }^{ 2 } }{ { b }^{ 3 }+{ 3a }^{ 2 }b } =\frac { 63 }{ 62 } \)
By componendo and dividendo

a : b = 3 : 2

Question 18.
Give \(\frac { { x }^{ 3 }+12x }{ { 6x }^{ 2 }+8 } =\frac { { y }^{ 3 }+27y }{ { 9y }^{ 2 }+27 } \) Using componendo and dividendo find x : y.
Solution:
Give \(\frac { { x }^{ 3 }+12x }{ { 6x }^{ 2 }+8 } =\frac { { y }^{ 3 }+27y }{ { 9y }^{ 2 }+27 } \)
Using componendo-dividendo, we have

Question 19.
Using the properties of proportion, solve the following equation for x; given
\(\frac { x^{ 3 }+3x }{ { 3x }^{ 2 }+1 } =\frac { 341 }{ 91 } \)
Solution:
\(\frac { x^{ 3 }+3x }{ { 3x }^{ 2 }+1 } =\frac { 341 }{ 91 } \)
Applying componendo and dividendo

Question 20.
If \(\frac { x+y }{ ax+by } =\frac { y+z }{ ay+bz } =\frac { z+x }{ az+bx } \) , prove that each of these ratio is equal to \(\\ \frac { 2 }{ a+b } \) unless x + y + z = 0
Solution:
\(\frac { x+y }{ ax+by } =\frac { y+z }{ ay+bz } =\frac { z+x }{ az+bx } \)
= \(\frac { x+y+y+z+z+x }{ ax+by+ay+bz+az+bx } \)

Hope given ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 7 Ratio and Proportion Ex 7.3 are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.
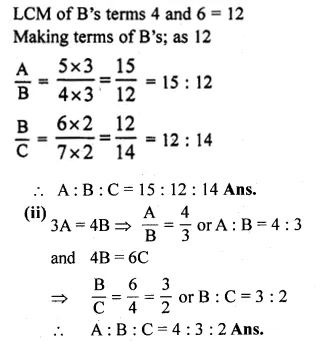
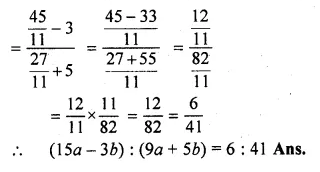