NCERT Solutions for Class 9 Maths Chapter 12 Constructions Ex 12.2 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 12 Constructions Ex 12.2.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 9 |
| Subject | Maths |
| Chapter | Chapter 12 |
| Chapter Name | Constructions |
| Exercise | Ex 12.2 |
| Number of Questions Solved | 5 |
| Category | NCERT Solutions |
NCERT Solutions for Class 9 Maths Chapter 12 Constructions Ex 12.2
Question 1.
Construct a ∆ ABC in which BC = 7 cm, ∠B = 75° and AB + AC = 13 cm.
Solution:
Given that, in ∆ ABC, BC = 7 cm, ∠B = 75° and AS + AC = 13 cm
Steps of construction
- Draw the base BC = 7 cm
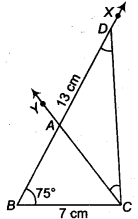
- At the point 6 make an ∠XBC = 75°.
- Cut a line segment BD equal to AB + AC = 13 cm from the ray BX.
- Join DC.
- Make an ∠DCY = ∠BDC.
- Let CY intersect BX at A.
Then, ABC is the required triangle.
Question 2.
Construct a ∆ ABC in which BC = 8 cm, ∠B = 45° and AB – AC = 35 cm.
Solution:
Given that, in ∆ ABC,
BC = 8 cm, ∠B = 45°and AB – AC = 3.5 cm
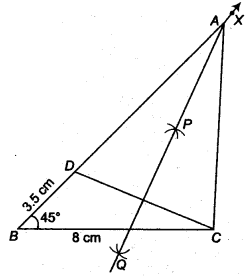
Steps of construction
- Draw the base BC = 8 cm
- At the point B make an ∠XBC = 45°.
- Cut the line segment BD equal to AB – AC = 3.5 cm from the ray BX.
- Join DC.
- Draw the perpendicular bisector, say PQ of DC.
- Let it intersect BX at a point A
- Join AC.
Question 3.
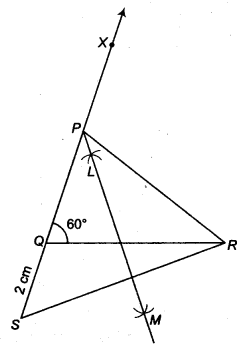
Construct a ∆ ABC in which QR = 6 cm, ∠Q = 60° and PR – PQ = 2 cm.
Solution:
Given that, in ∆ ABC, QR = 6 crn ∠Q = 60° and PR – PQ = 2 cm
Steps of construction
- Draw the base QR = 6 cm
- At the point Q make an ∠XQR = 60°.
- Cut line segment QS = PR- PQ (= 2 cm) from the line QX extended on opposite side of line segment QR.
- Join SR.
- Draw the perpendicular bisector LM of SR.
- Let LM intersect QX at P.
- Join PR.
Question 4.
Construct a ∆ XYZ in which ∠Y = 30°, ∠Y = 90° and XY + YZ + ZX = 11 cm.
Solution:
Given that, in ∆XYZ ∠Y = 30°, ∠Z = 90° and XY + YZ + ZX = 11cm
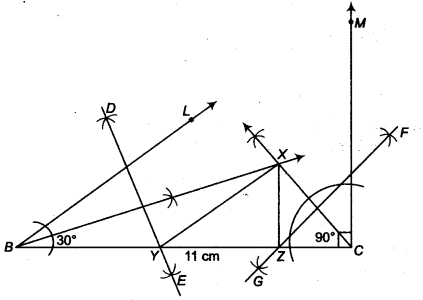
Steps of construction
- Draw a line segment BC = XY + YZ + ZX = 11 cm
- Make ∠LBC = ∠Y = 30° and ∠MCB = ∠Z = 90°.
- Bisect ∠LBC and ∠MCB. Let these bisectors meet at a point X.
- Draw perpendicular bisectors DE of XB and FG of XC.
- Let DE intersect BC at Y and FC intersect BC at Z.
- Join XY and XZ.
Then, XYZ is the required triangle.
Question 5.
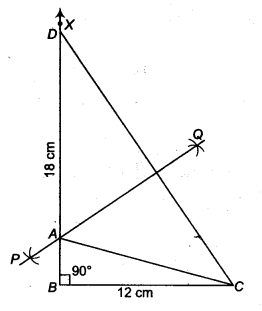
Construct a right triangle whose base is 12 cm and sum of its hypotenuse and other side is 18 cm.
Solution:
Given that, in A ABC, base BC = 12 cm, ∠B = 90° and AB + BC= 18 cm.
Steps of construction
- Draw the base BC = 12 cm
- At the point 6, make an ∠XBC = 90°.
- Cut a line segment BD = AB+ AC = 18 cm from the ray BX.
- Join DC.
- Draw the perpendicular bisector PQ of CD to intersect SD at a point A
Join AC.
Then, ABC is the required right triangle.