NCERT Solutions for Class 9 Maths Chapter 12 Constructions Ex 12.2

NCERT Solutions for Class 9 Maths Chapter 12 Constructions Ex 12.2 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 12 Constructions Ex 12.2.

Board	CBSE
Textbook	NCERT
Class	Class 9
Subject	Maths
Chapter	Chapter 12
Chapter Name	Constructions
Exercise	Ex 12.2
Number of Questions Solved	5
Category	NCERT Solutions

NCERT Solutions for Class 9 Maths Chapter 12 Constructions Ex 12.2

Question 1.
Construct a ∆ ABC in which BC = 7 cm, ∠B = 75° and AB + AC = 13 cm.
Solution:
Given that, in ∆ ABC, BC = 7 cm, ∠B = 75° and AS + AC = 13 cm
Steps of construction

1. Draw the base BC = 7 cm
   
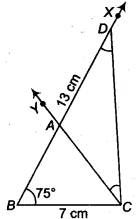
2. At the point 6 make an ∠XBC = 75°.
3. Cut a line segment BD equal to AB + AC = 13 cm from the ray BX.
4. Join DC.
5. Make an ∠DCY = ∠BDC.
6. Let CY intersect BX at A.
   Then, ABC is the required triangle.

Question 2.
Construct a ∆ ABC in which BC = 8 cm, ∠B = 45° and AB – AC = 35 cm.
Solution:
Given that, in ∆ ABC,
BC = 8 cm, ∠B = 45°and AB – AC = 3.5 cm

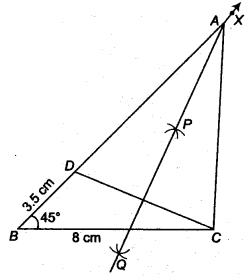
Steps of construction

1. Draw the base BC = 8 cm
2. At the point B make an ∠XBC = 45°.
3. Cut the line segment BD equal to AB – AC = 3.5 cm from the ray BX.
4. Join DC.
5. Draw the perpendicular bisector, say PQ of DC.
6. Let it intersect BX at a point A
7. Join AC.

Question 3.
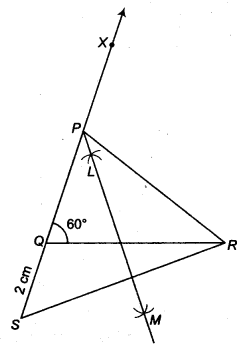
Construct a ∆ ABC in which QR = 6 cm, ∠Q = 60° and PR – PQ = 2 cm.
Solution:
Given that, in ∆ ABC, QR = 6 crn ∠Q = 60° and PR – PQ = 2 cm
Steps of construction

1. Draw the base QR = 6 cm
2. At the point Q make an ∠XQR = 60°.
3. Cut line segment QS = PR- PQ (= 2 cm) from the line QX extended on opposite side of line segment QR.
4. Join SR.
5. Draw the perpendicular bisector LM of SR.
6. Let LM intersect QX at P.
7. Join PR.
   

Question 4.
Construct a ∆ XYZ in which ∠Y = 30°, ∠Y = 90° and XY + YZ + ZX = 11 cm.
Solution:
Given that, in ∆XYZ ∠Y = 30°, ∠Z = 90° and XY + YZ + ZX = 11cm

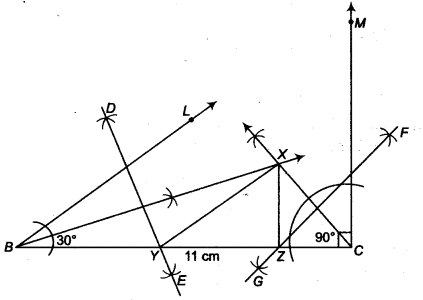
Steps of construction

1. Draw a line segment BC = XY + YZ + ZX = 11 cm
2. Make ∠LBC = ∠Y = 30° and ∠MCB = ∠Z = 90°.
3. Bisect ∠LBC and ∠MCB. Let these bisectors meet at a point X.
4. Draw perpendicular bisectors DE of XB and FG of XC.
5. Let DE intersect BC at Y and FC intersect BC at Z.
6. Join XY and XZ.
   Then, XYZ is the required triangle.

Question 5.
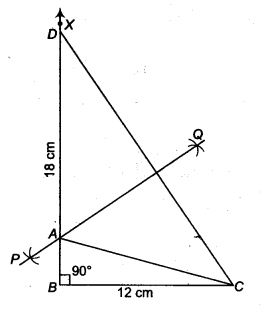
Construct a right triangle whose base is 12 cm and sum of its hypotenuse and other side is 18 cm.
Solution:
Given that, in A ABC, base BC = 12 cm, ∠B = 90° and AB + BC= 18 cm.
Steps of construction

1. Draw the base BC = 12 cm
2. At the point 6, make an ∠XBC = 90°.
3. Cut a line segment BD = AB+ AC = 18 cm from the ray BX.
4. Join DC.
5. Draw the perpendicular bisector PQ of CD to intersect SD at a point A

Join AC.
Then, ABC is the required right triangle.