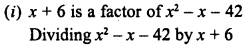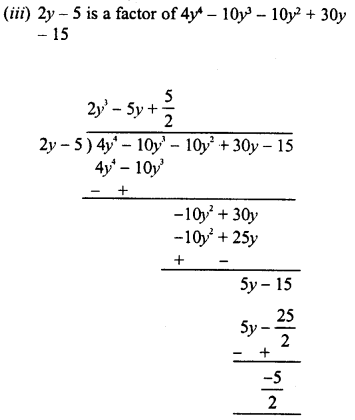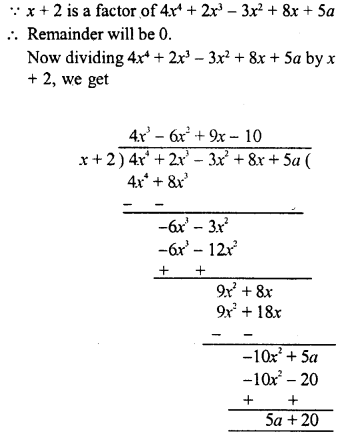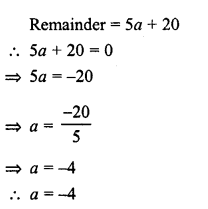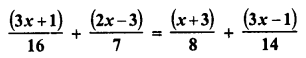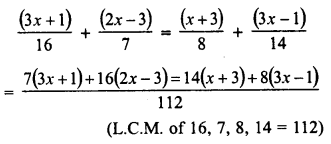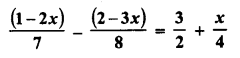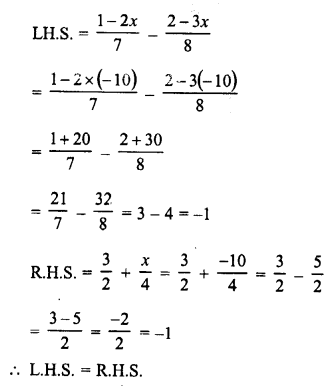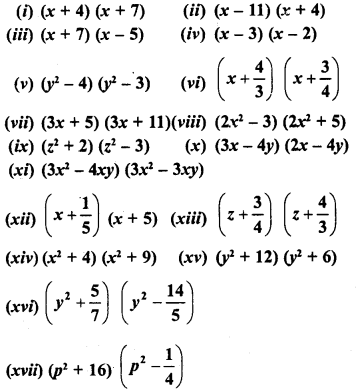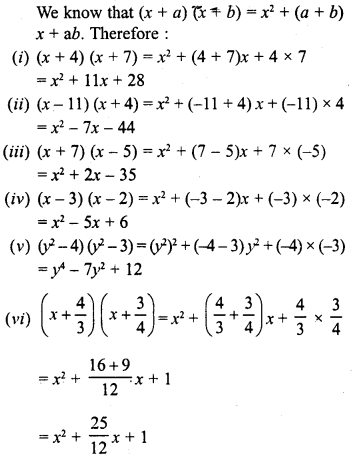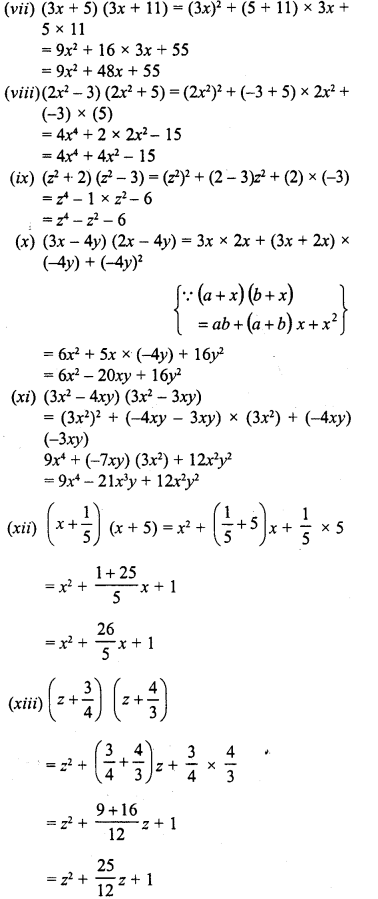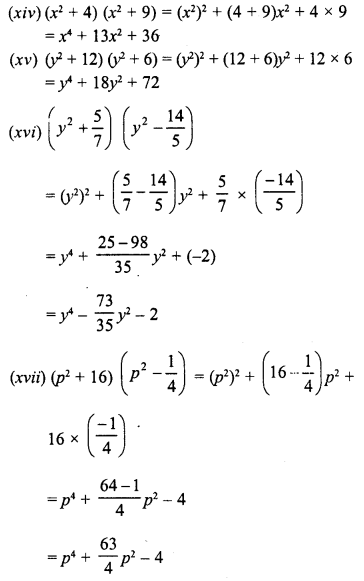RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.4
These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.4
Other Exercises
- RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.1
- RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.2
- RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.3
- RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.4
- RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.5
- RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.6
- RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.7
- RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.8
- RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.9
Factorize each of the following expressions :
Question 1.
qr-pr + qs – ps
Solution:
qr- pr + qs-ps
Arranging in suitable groups = r(q-p) +s (q-p) {(q – p) is common}
= (q-p) (r + s)
Question 2.
p2q -pr2-pq + r2
Solution:
p2q -pr2-pq + r2
= p2q -pq-pr2 + r2 (Arranging in group)
= pq(p- 1)-r2(p-1) {(p – 1) is common}
= (p – 1) (pq – r2)
Question 3.
1 + x + xy + x2y
Solution:
1 + x + xy + x 2y
= 1 (1 + x) +xy (1 +x)
= (1 + x) (1 + xy) {(1 + x) is common}
Question 4.
ax + ay – bx – by
Solution:
ax + ay – bx – by
= a (x + y) – b (x + y) {(x + y) is coinmon}
= (x+y) (a- b)
Question 5.
xa2 + xb2 -ya2 – yb2
Solution:
xa2 + xb2 – ya2 – yb2
= x (a2 + b2) -y (a2 + b2) {(a2 + b2) is common}
= {a2 + b2) (x -y)
Question 6.
x2 + xy + xz + yz
Solution:
x2 + xy + xz + yz
= x (x + y) + z(x + y) {(x + y) is common}
= (x + y) (x + z)
Question 7.
2ax + bx + 2ay + by
Solution:
2ax + bx + 2ay + by
= x {2a + b) + y (2a + b) {(2a + b) is common}
= (2a + b) (x + y)
Question 8.
ab- by- ay +y2
Solution:
ab – by – ay + y2
= b(a-y)-y(a-y) {(a -y) is common}
= (a-y) (b – y)
Question 9.
axy + bcxy -az- bcz
Solution:
axy + bcxy – az – bcz
= xy (a + bc) – z (a + bc) {(a + bc) is common}
= (a + bc) (xy – z)
Question 10.
lm2 – mn2 – lm + n2
Solution:
lm2 – mn2 – lm + n2
= m (lm – n2)- 1 (lm – n2) {(lm – n2) is common}
= (lm – n2) (m – 1)
Question 11.
x3 – y2 + x – x2y2
Solution:
x3 -y2 + x – x2y2
⇒ x3 + x – x2y2 – y2
= x(x2+ 1)-y2(x2+ 1) {(x2 + 1) is common}
= (x2 + 1) (x -y2)
Question 12.
6xy + 6 – 9y – 4x
Solution:
6xy + 6 – 9y – 4x
= 6 xy – 4x – 9y + 6
= 2x (3y – 2) – 3 (3y – 2) {(3y – 2) is common}
= (3y-2) (2x – 3)
Question 13.
x2 – 2ax – 2ab + bx
Solution:
x2 – 2ax – 2ab + bx
⇒ x2 – 2ax + bx – 2ab
= x (x – 2a) + b (x – 2a) {(x – 2a) is common}
= (x – 2a) (x + b)
Question 14.
x3 – 2x2y + 3xy2 – 6y3
Solution:
x3 – 2x2y + 3xy2 – 6y3
= x2 (x – 2y) + 3y2 (x – 2y) {(x – 2y) is common}
= (x – 2y) (x2 + 3y2)
Question 15.
abx2 + (ay – b) x-y
Solution:
abx2 + (ay – b) x-y
= abx2 + ayx – bx -y
= ax (bx + y) – 1 (bx + y) {(bx +y) is common}
= (bx + y) (ax – 1)
Question 16.
(ax + by)2 + (bx – ay)2
Solution:
(ax + by)2 + (bx – ay)2
= a2x2 + b2y2 + 2abxy + b2x2 + a2y2 – 2abxy
= a2x2 + b2y2 + b2x2 + a2y2
= a2x2 + b2x2 + a2y2 + by2
= x2 (a2 + b2) + y2 (a2 + b2) {(a2 + b2) is common}
= (a2 + b2) (x2 + y2)
Question 17.
16 (a – b)3 -24 (a- b)2
Solution:
16 (a – b)3 -24 (a- b)2
HCF of 16, 24 = 8
and HCF of (a – b)3, (a – b)2 = (a – b)2
∴16 (a – b)3 – 24 (a – b)2
= 8 (a-b)2 {2 (a-b)- 3}
{8 (a – b)2 is common}
= 8 (a – b)2 (2a – 2b – 3)
Question 18.
ab (x2 + 1) + x (a2 + b2)
Solution:
ab (x2 + 1) + x (a2 + b2)
= abx2 + ab + a2x + b2x
= abx2 + b2x + a2x + ab
= bx (ax + b) + a (ax + b) {(ax + b) is common}
= (ax + b) (bx + a)
Question 19.
a2x2 + (ax2 + 1) x + a
Solution:
a2x2 + (ax2 + 1) x + a
= a2x2 + ax3 + x + a
= ax3 + a2x2 + x + a
= ax2 (x + a) + 1 (x + a) {(x + a) is common}
= (x + a) (ax2 + 1)
Question 20.
a(a- 2b -c) + 2bc
Solution:
a(a- 2b -c) + 2bc
= a2– 2ab -ac +2bc
= a (a – 2b) – c (a – 2b) {(a – 2b) is common}
= (a – 2b) (a – c)
Question 21.
a (a + b – c)- bc
Solution:
a (a + b – c) – bc
= a2 + ab – ac – bc
= a (a + b) – c (a + b) {(a + b) is common}
= (a + b) (a – c)
Question 22.
x2 – 11xy – x +11y
Solution:
x2 – 11xy-x + 11y
= x2 -x – 11 xy + 11 y
= x (x – 1) – 11y (x – 1) {(x – 1) is common}
= (x- 1) (x- 11y)
Question 23.
ab – a – b + 1
Solution:
ab – a-b + 1
= a (b – 1) – 1 (b – 1) {(b – 1) is common}
= (b – 1) (a – 1)
Question 24.
x2 + y – xy – x
Solution:
x2 + y – xy – x
= x2 – x- xy + y
= x (x – 1) – y (x – 1) {(x – 1) is common}
= (x- 1) (x-y)
Hope given RD Sharma Class 8 Solutions Chapter 7 Factorizations Ex 7.4 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.