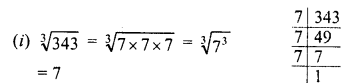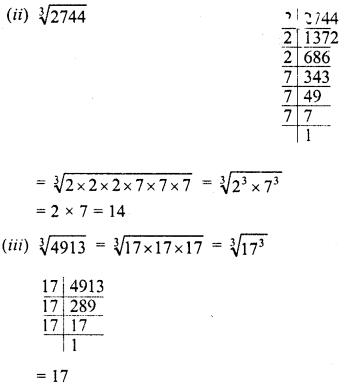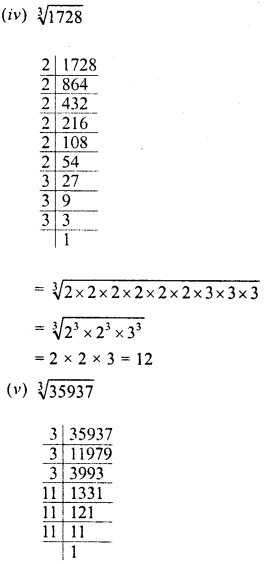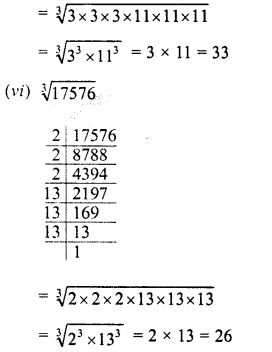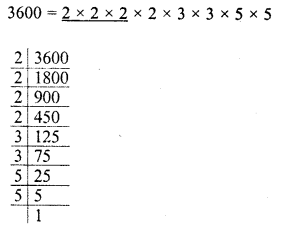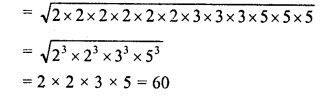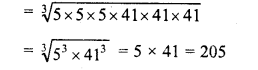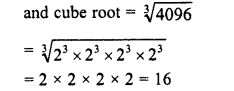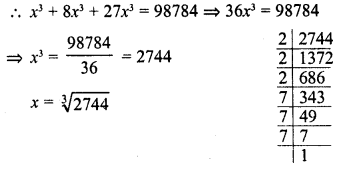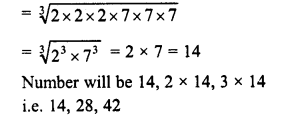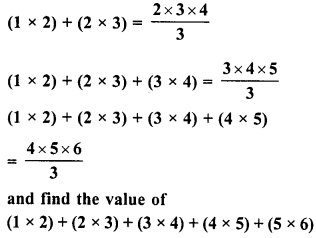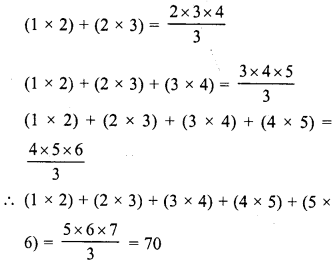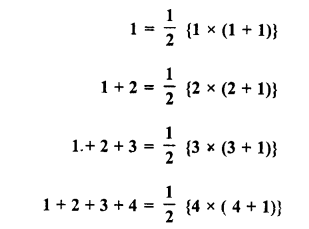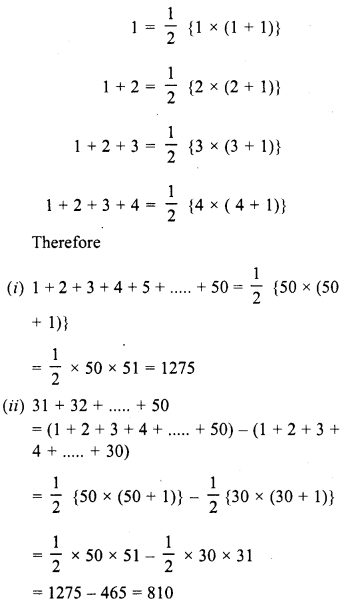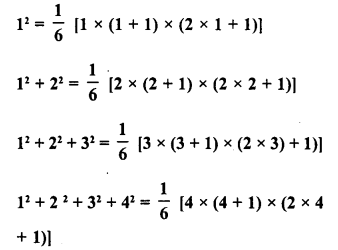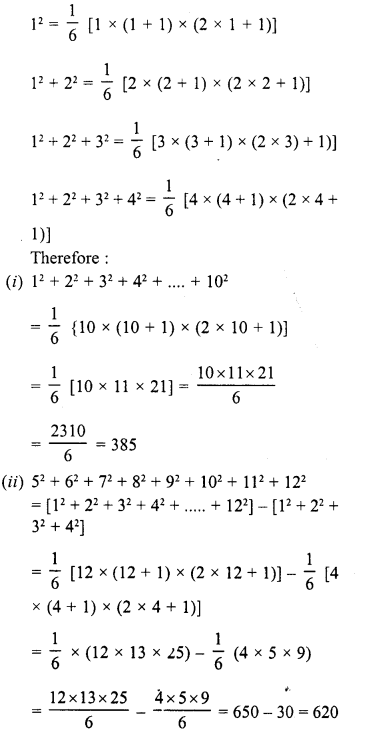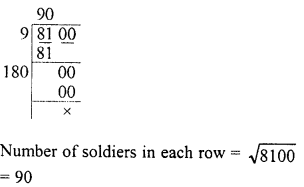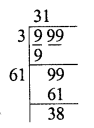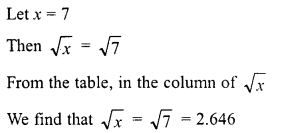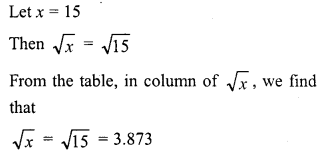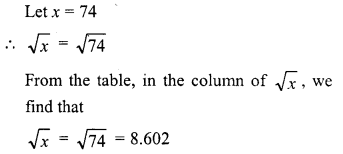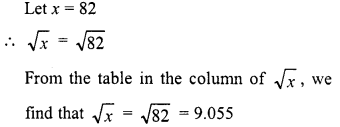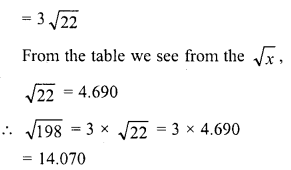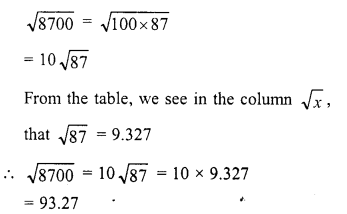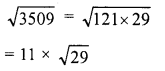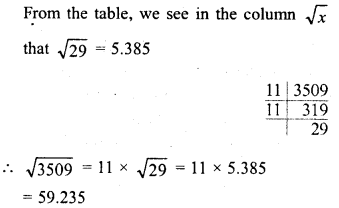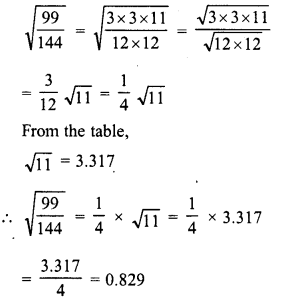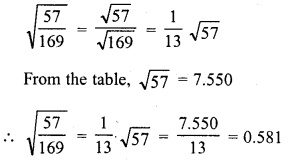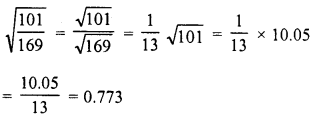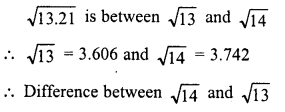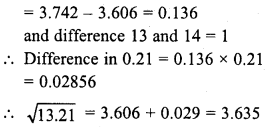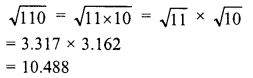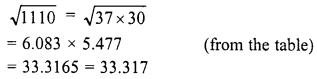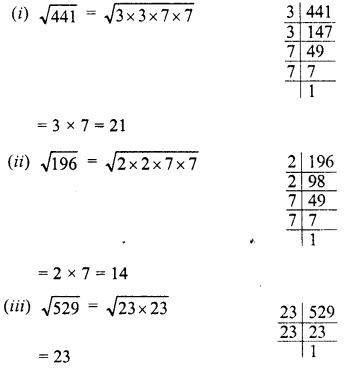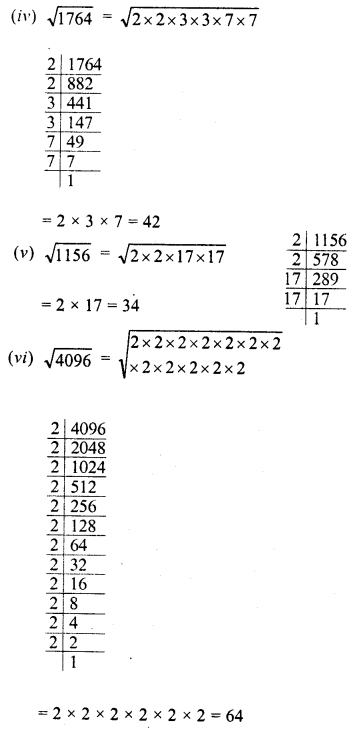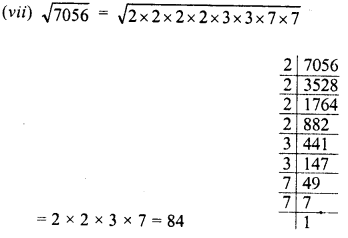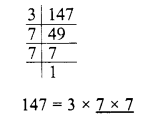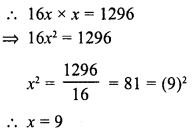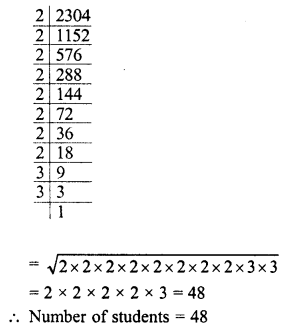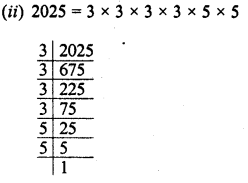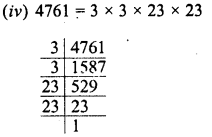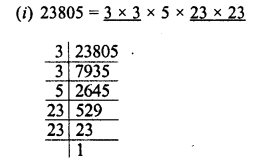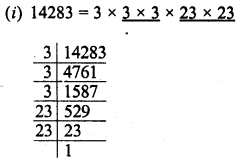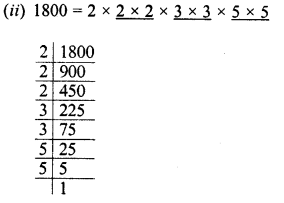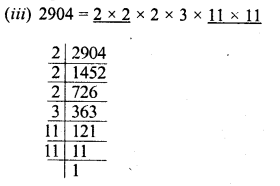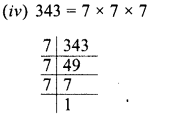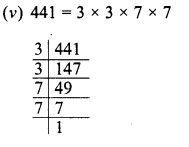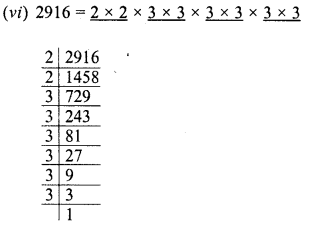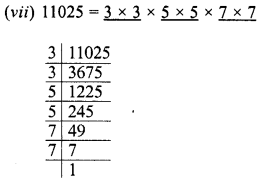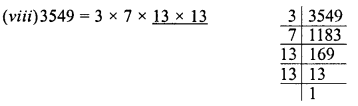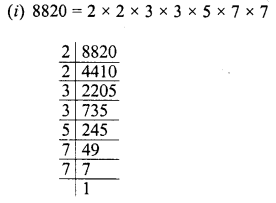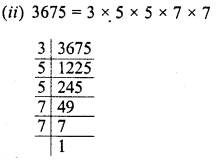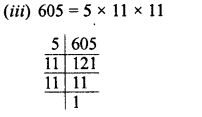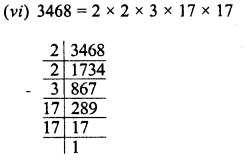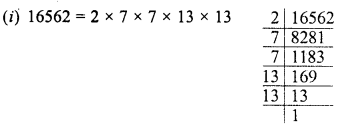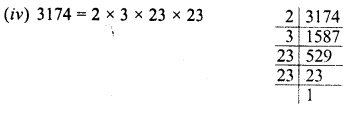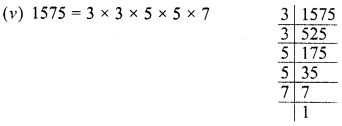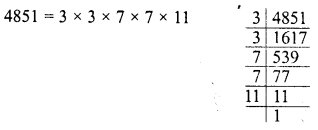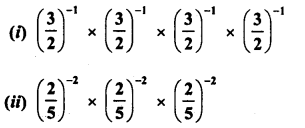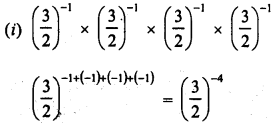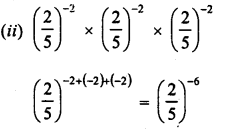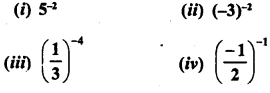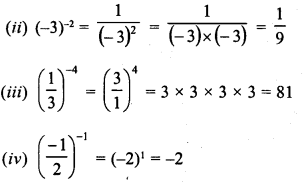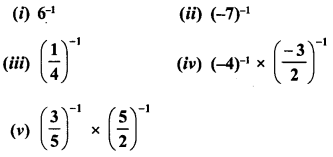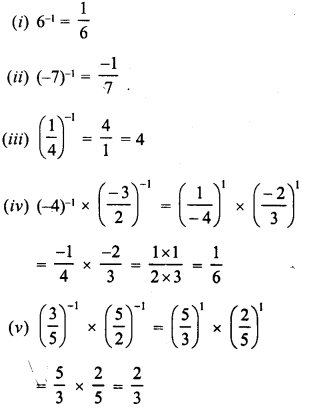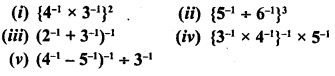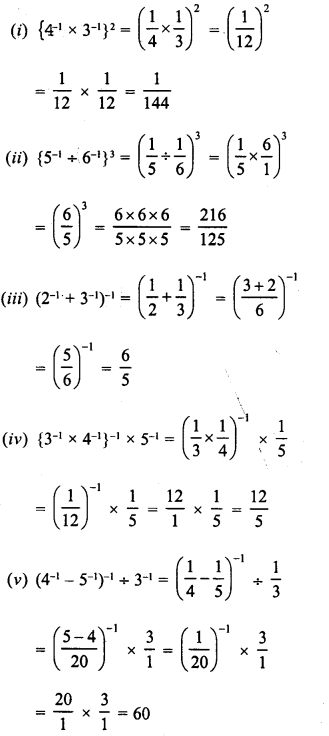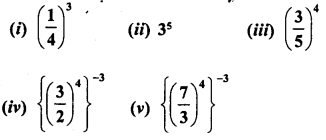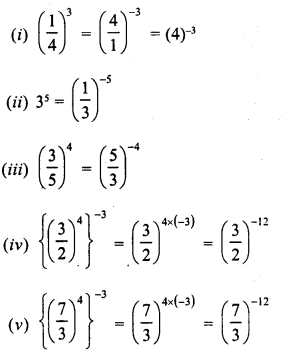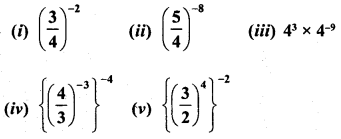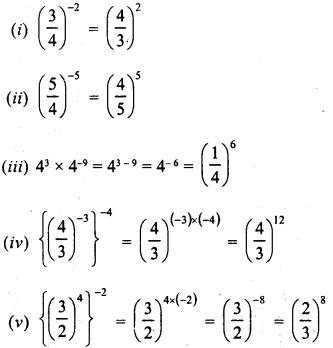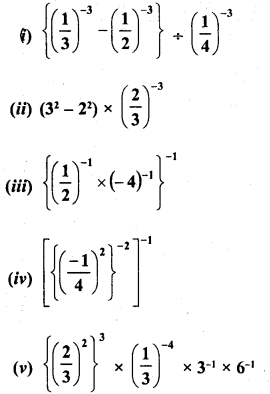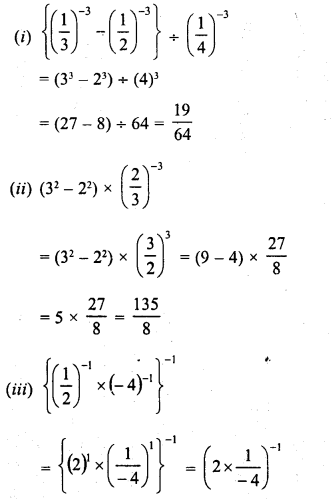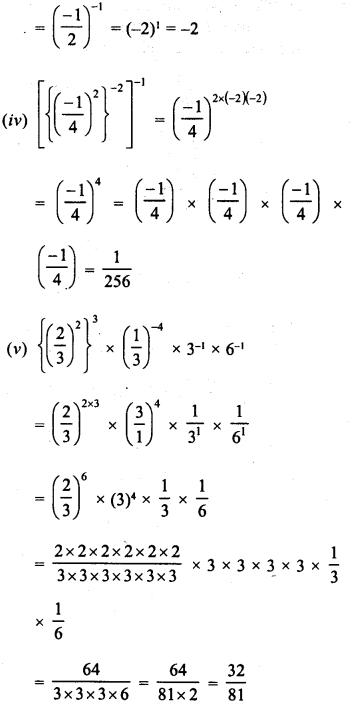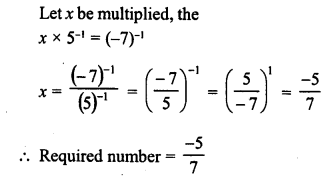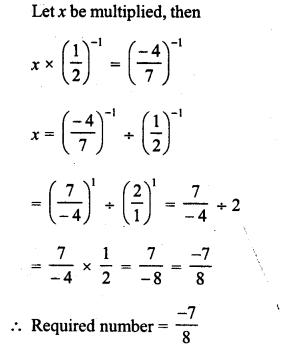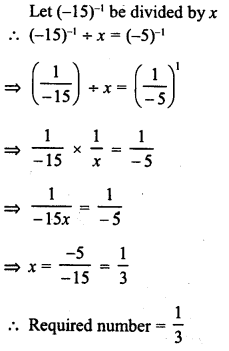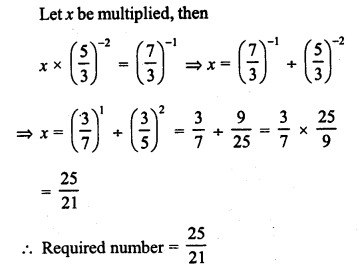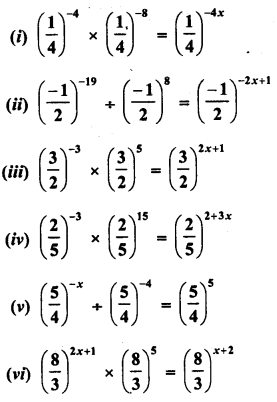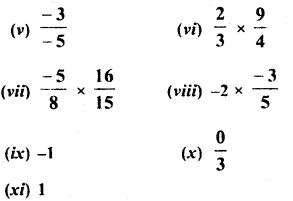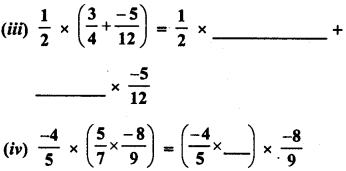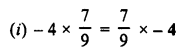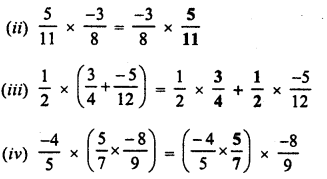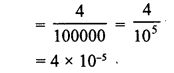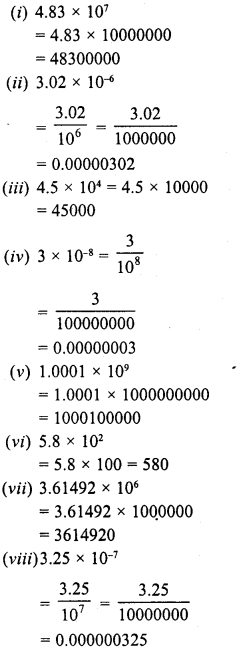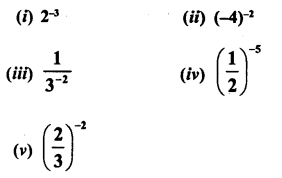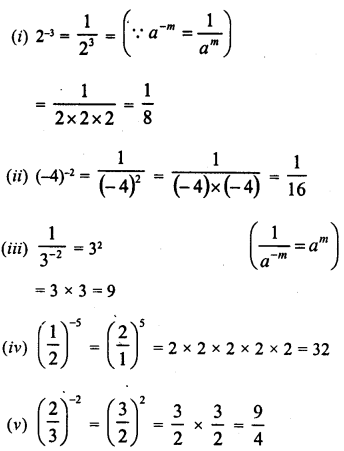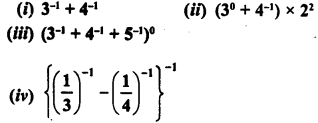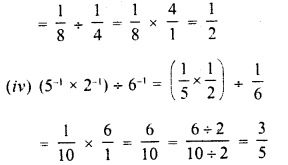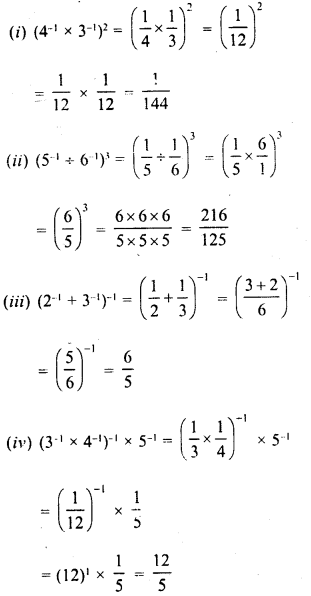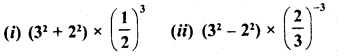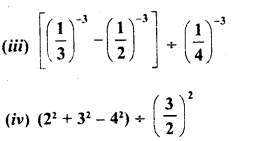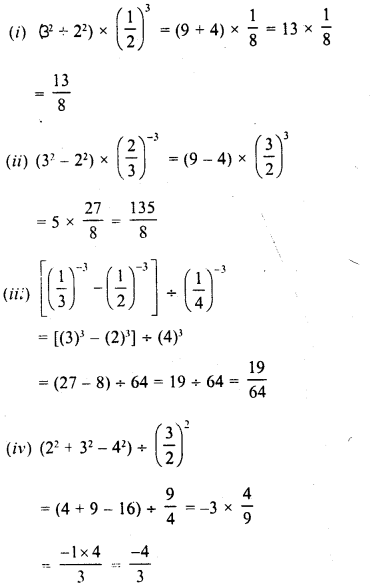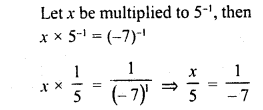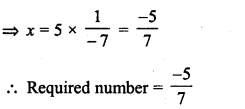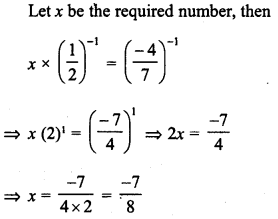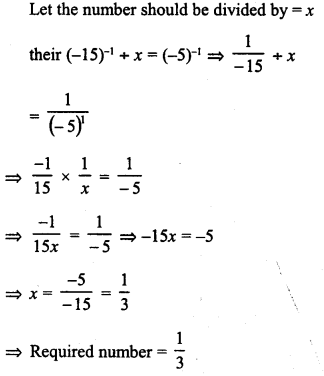RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7
These Solutions are part of RD Sharma Class 8 Solutions. Here we have given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7
Other Exercises
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.1
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.2
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.3
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.4
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.5
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.6
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.8
- RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.9
Find the square root of the following numbers in decimal form :
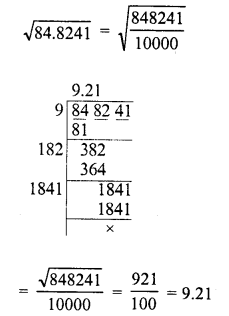
Question 1.
84.8241
Solution:
Question 2.
0.7225
Solution:
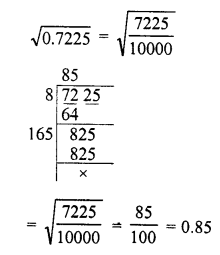
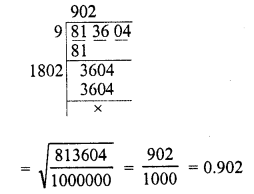
Question 3.
0.813604
Solution:
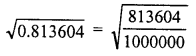
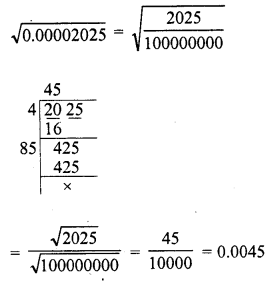
Question 4.
0.00002025
Solution:
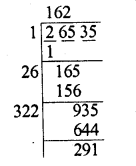
Question 5.
150.0625
Solution:

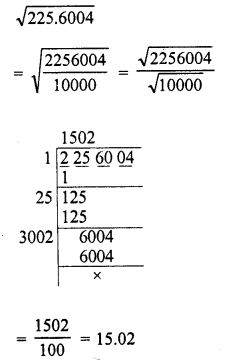
Question 6.
225.6004
Solution:
Question 7.
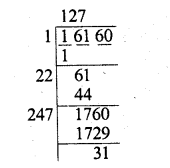
3600.720036
Solution:

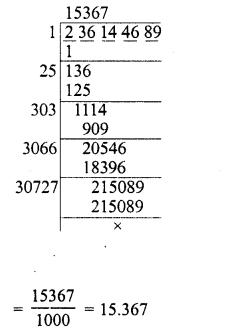
Question 8.
236.144689
Solution:

Question 9.
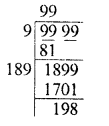
0.00059049
Solution:

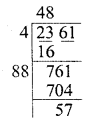
Question 10.
176.252176
Solution:
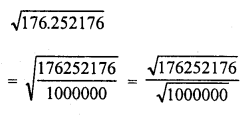
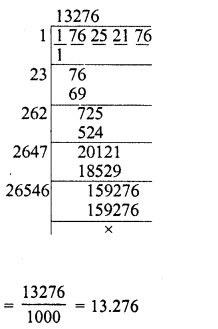
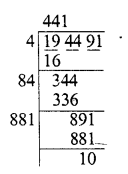
Question 11.
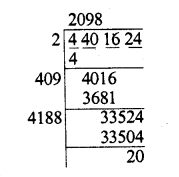
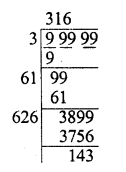
9998.0001
Solution:
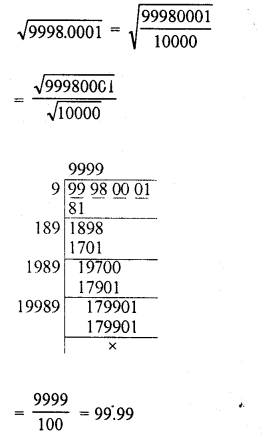
Question 12.
0.00038809
Solution:
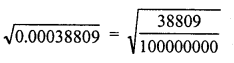
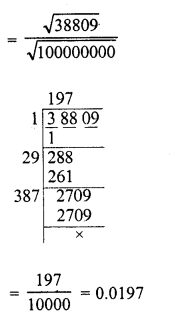
Question 13.
What is that fraction which when multiplied by itself gives 227.798649 ?
Solution:

Question 14.
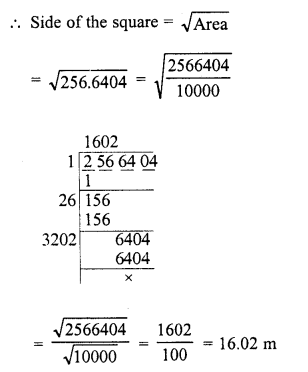
square playground is 256.6404 square metres. Find the length of one side of the playground.
Solution:
Area of square playground = 256.6404 sq. m
Question 15.
What is the fraction which when multiplied by itself gives 0.00053361 ?
Solution:

Question 16.
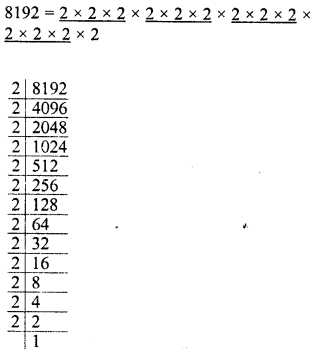
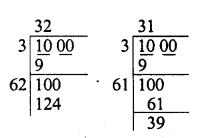
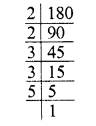
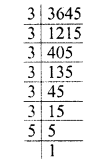
Simplify :
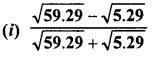
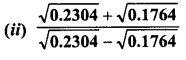
Solution:

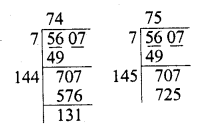
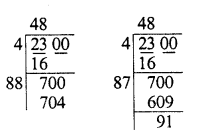
Question 17.
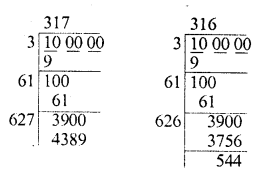
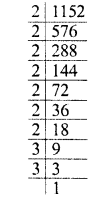
Evaluate \(\sqrt { 50625 }\) and hence find the value of \(\sqrt { 506.25 } +\sqrt { 5.0625 } \).
Solution:
![]()

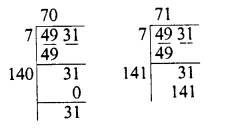
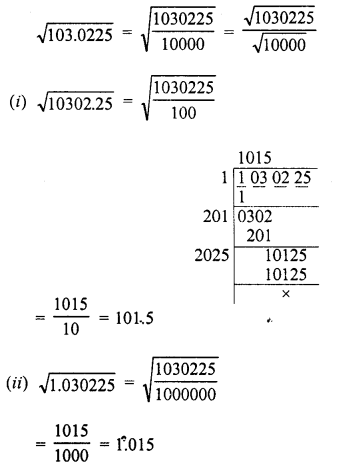
Question 18.
Find the value of \(\sqrt { 103.0225 }\) and hence And the value of
![]()
Solution:
Hope given RD Sharma Class 8 Solutions Chapter 3 Squares and Square Roots Ex 3.7 are helpful to complete your math homework.
If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.