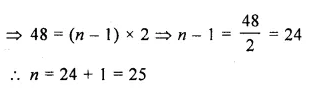Tag: Selina ICSE Solutions for Class 10 Maths

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10A

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10A

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10E
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10F

Question 1.
Which of the following sequences are in arithmetic progression?
(i) 2, 6, 10, 14, …….
(ii) 15, 12, 9, 6,…….
(iii) 5, 9, 12, 18, ……
(iv) \(\frac { 1 }{ 2 } ,\frac { 1 }{ 3 } ,\frac { 1 }{ 4 } ,\frac { 1 }{ 5 } \),…..
Solution:
(i) 2, 6, 10, 14,
Here, d = 6 – 2 = 4
10 – 6 = 4
14 – 10 = 4
∴ In each case (d) is same.
∴It is an arithmetic progression.


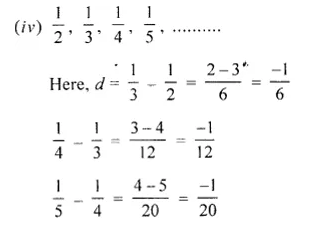
∴d is not the same
∴It is not an arithmetic progression

Question 2.
The nth term of a sequence is (2n – 3), find its fifteenth term.
Solution:
T_n = 2n – 3
T₁₅ = 2 x 15 – 3
= 30 – 3
= 27

Question 3.
If the pth term of an A.P. is (2p + 3); find the A.P.
Solution:
T_p = 2p + 3
T₁ = 2 x 1 + 3 = 2 + 3 = 5
T₂ = 2 x 2 + 3 = 4 + 3 = 7
T₃ = 2 x 3 + 3 = 6 + 3 = 9
∴A.P. is 5, 7, 9,…..

Question 4.
Find the 24th term of the sequence : 12, 10, 8, 6,…….
Solution:
A.P. is 12, 10, 8, 6,……
Here a = 12, d = 10 – 12 = – 2
T_n = a + (n – 1)d
T₂₄ = 12 + (24 – 1) x ( – 2)
= 12 + 23 x ( – 2)
= 12 – 46
= – 34

Question 5.
Find the 30th term of the sequence :
\(\\ \frac { 1 }{ 2 } \), 1, \(\\ \frac { 3 }{ 2 } \),….
Solution:
\(\\ \frac { 1 }{ 2 } \), 1, \(\\ \frac { 3 }{ 2 } \),….
Here a = \(\\ \frac { 1 }{ 2 } \), d = \(1- \frac { 1 }{ 2 } \)
\(\\ \frac { 1 }{ 2 } \)

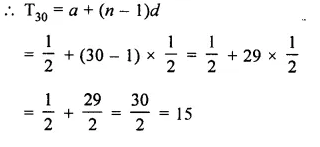
Question 6.
Find the 100th term of the sequence :
√3, 2√3, 3√3,….
Solution:
√3, 2√3, 3√3,….
Here a = √3, d = 2√3 – √3 = √3

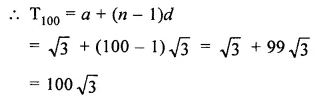
Question 7.
Find the 50th term of the sequence :
\(\\ \frac { 1 }{ n } \), \(\\ \frac { n+1 }{ n } \), \(\\ \frac { 2n+1 }{ n } \),……
Solution:
\(\\ \frac { 1 }{ n } \), \(\\ \frac { n+1 }{ n } \), \(\\ \frac { 2n+1 }{ n } \),……
=>\(\\ \frac { 1 }{ n } \), \(1+ \frac { 1 }{ n } \), \(2+ \frac { 1 }{ n } \),…..

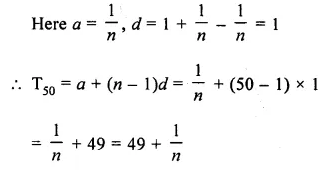
Question 8.
Is 402 a term of the sequence :
8, 13, 18, 23,…?
Solution:
In sequence 8, 13, 18, 23,…..
a = 8 and d = 13 – 8 = 5
Let 402 be the nth term, then
402 = a + (n – 1)d = 8 + (n – 1) x 5
\(\\ \frac { 402-8 }{ 5 } \) = n – 1
=> \(\\ \frac { 394 }{ 5 } \) = n – 1
394 is not exactly divisible by 5,
∴ 402 is not its term.

Question 9.
Find the common difference and 99th term of the arithmetic progression :
\(7 \frac { 3 }{ 4 } \), \(9 \frac { 1 }{ 2 } \), \(11 \frac { 1 }{ 4 } \),…..
Solution:
\(7 \frac { 3 }{ 4 } \), \(9 \frac { 1 }{ 2 } \), \(11 \frac { 1 }{ 4 } \),…..
here a = \(7 \frac { 3 }{ 4 } \)
= \(\\ \frac { 31 }{ 4 } \)

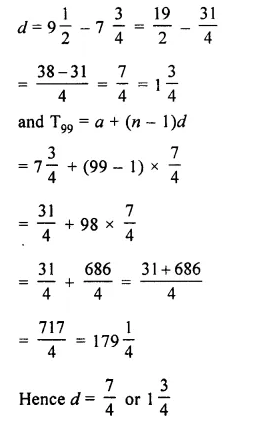
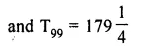
Question 10.
How many terms are there in the series:
(i) 4, 7, 10, 13,…..148 ?
(ii) 0.5, 0.53, 0.56,…..1.1 ?
(iii) \(\\ \frac { 3 }{ 4 } \), 1, \(1 \frac { 1 }{ 4 } \),….3 ?
Solution:
(i) 4, 7, 10, 13,…..148 ?
Here a = 4, d = 7 – 4
= 3
Let 148 be the nth term, then

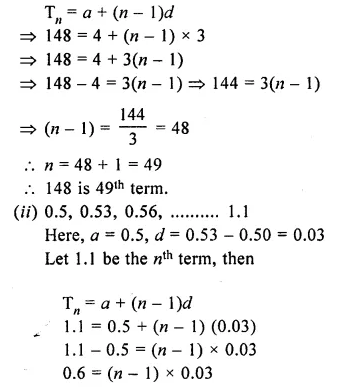
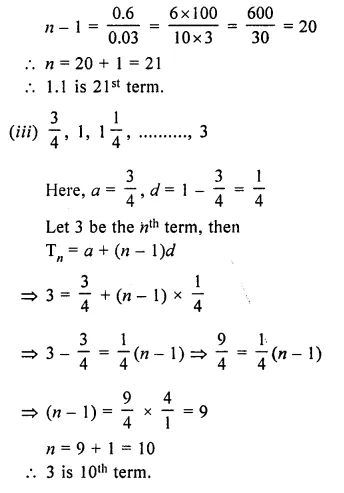
Question 11.
Which term of the A.P. 1 + 4 + 7 + 10 +……is 52 ?
Solution:
A.P. is 1, 4, 7, 10,……is 52
Here a = 1, d = 4 – 1 = 3
Let 52 be the nth term, then

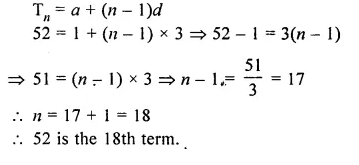
Question 12.
If 5th and 6th terms of an A.P. are respectively 6 and 5, find the 11th term of the A.P.
Solution:
5th term (T₅) = 6
=> 6 = a + 4d
and T₆ = 5
=> 5 = a + 5d

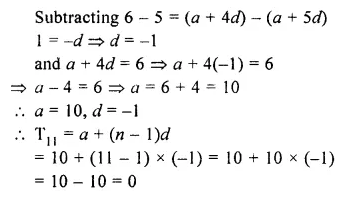
Question 13.
If t_n represents nth term of an A.P., t₂ + t₅ – t₃ = 10 and t₂ + t₉ = 17, find its first term and its common difference.
Solution:
Let first term of an A.P. be a
and common difference = d
Then T_n is the nth term

Question 14.
Find the 10th term from the end of the A.P. 4, 9, 14,…. 254.
Solution:
We know that rth term from the end
= (n – r + 1)th from the beginning
Here, a = A, d = 9 – 4 = 5,
nth term = 254

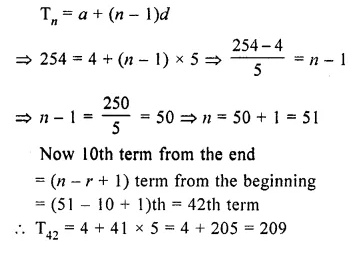
Question 15.
Determine the arithmetic progression whose 3rd term is 5 and 7th term is 9.
Solution:
Let a be the first term and d be the common difference, then
T₃ = a + 2d – 5
T₇ = a + 6d = 9

Question 16.
Find the 31st term of an A.P. whose 10th term is 38 and 16th term is 74.
Solution:
Let a be the first term and d be the common difference, then
T₁₀ = a + 9d =38
and T₁₆ = a + 15d = 74

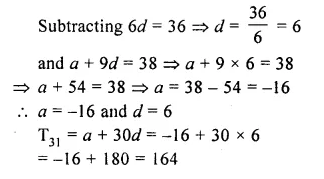
Question 17.
Which term of the series :
21, 18, 15, is – 81 ?
Can any term of this series be zero ? If yes, find the number of term.
Solution:
21, 18, 15, 1….. – 81
Here a = 21,d = 18 – 21 = – 3,
nth term = – 81

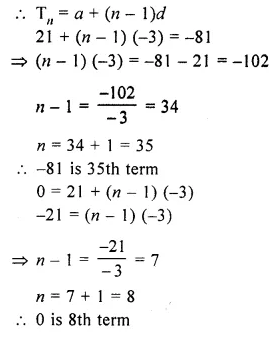
Question 18.
An A.P. consists of 60 terms. If the first and the last terms be 7 and 125 respectively, find the 31st term.
Solution:
Given : An A.P. consists of 60 terms
a = 7
and a₆₀ = 125
=> a + (60 – 1 )d = 125
=> 7 + 59 d = 125
=> 59d= 125 – 7
=> d = \(\\ \frac { 118 }{ 59 } \) = 2
now, a₃₁ = a + (n – 1)d
= 7 + (31 – 1) x 2
= 7 + 30 x 2
= 67

Question 19.
The sum of the 4th and the 8th terms of an A.P. is 24 and the sum of the sixth term and the tenth term is 34. Find the first three terms of the A.P.
Solution:
In an A.P.
T₄ + T₈ = 24
T₆ + T₁₀ =34
Let a be the first term and d be the common difference

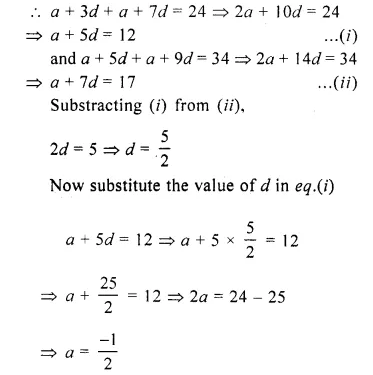
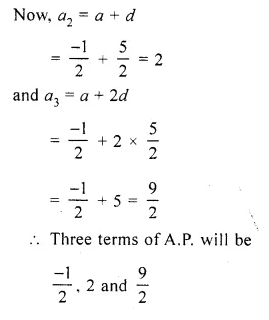
Question 20.
If the third term of an A.P. is 5 and the seventh terms is 9, find the 17th term
Solution:
Let the first term of an A.P. = a
and the common difference of the given A.P. = d
As, we know that,

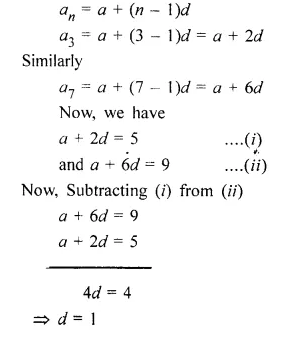
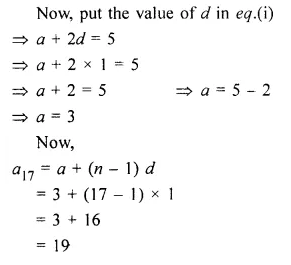
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 10 Arithmetic Progression Ex 10A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.