Tag: Selina ICSE Solutions for Class 10 Maths

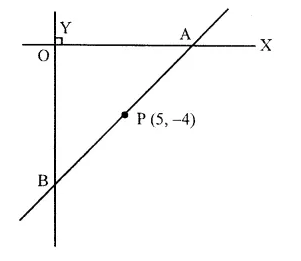
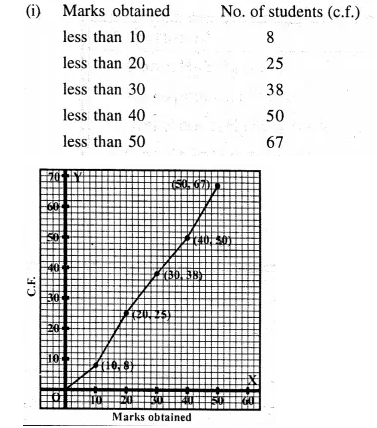
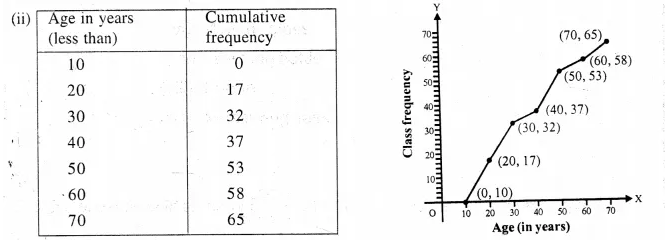
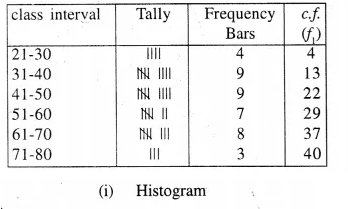
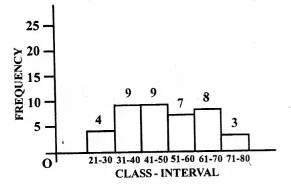
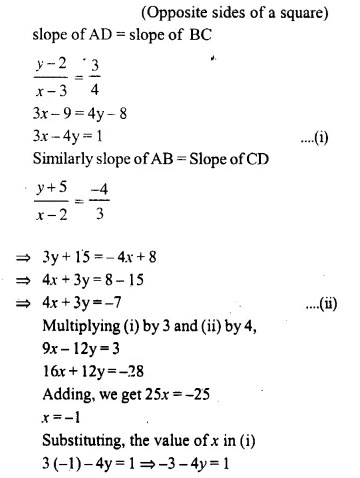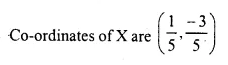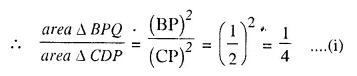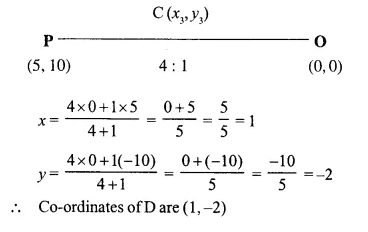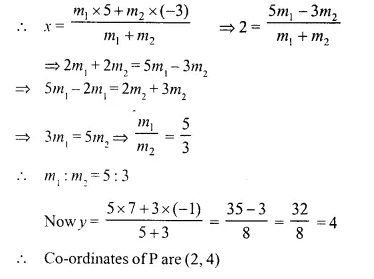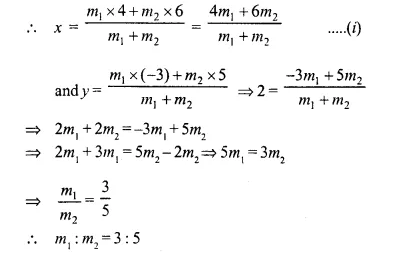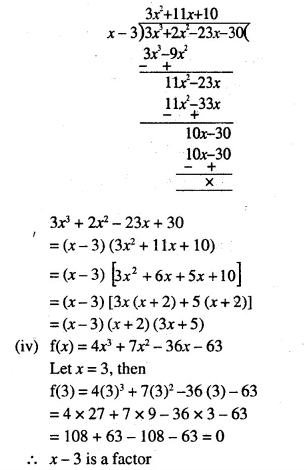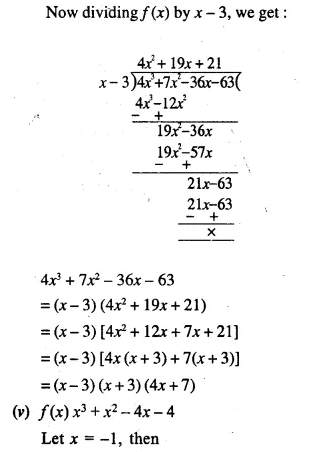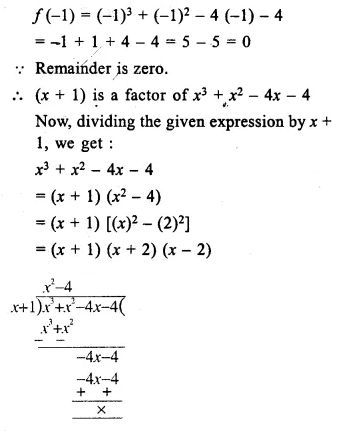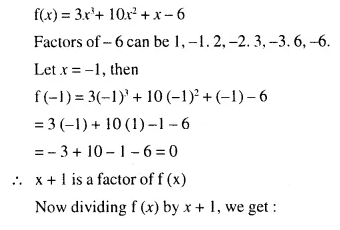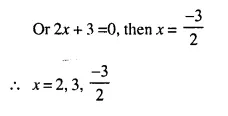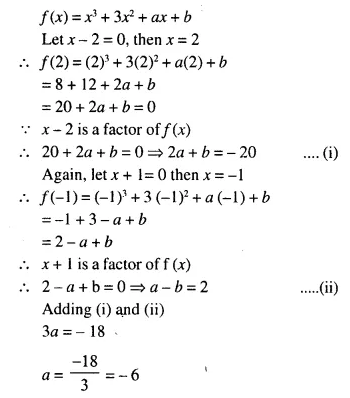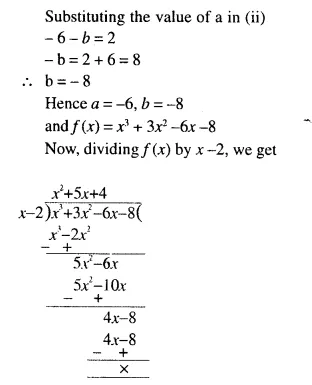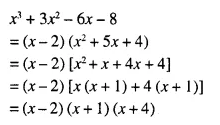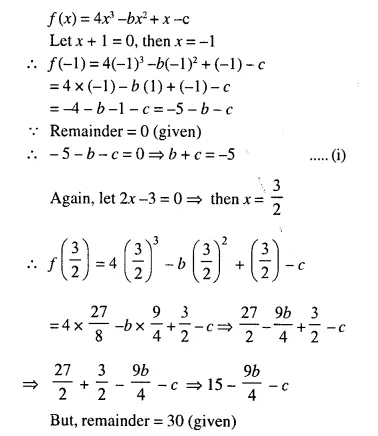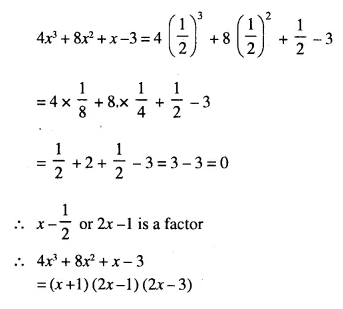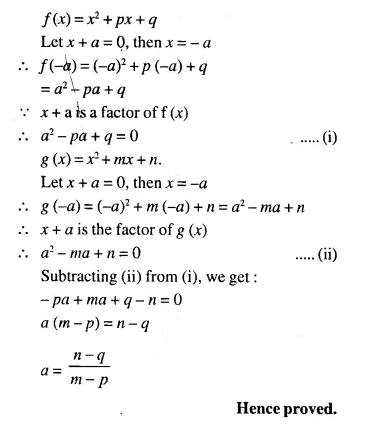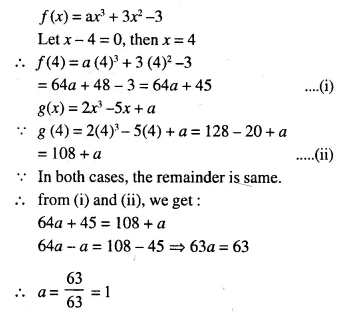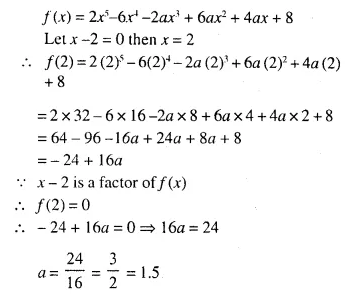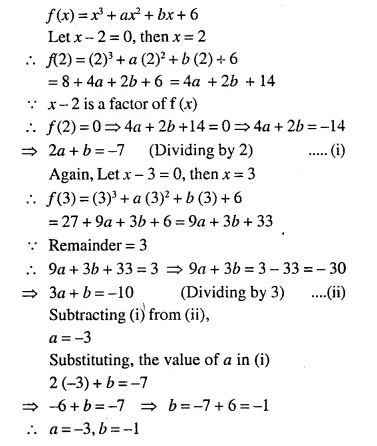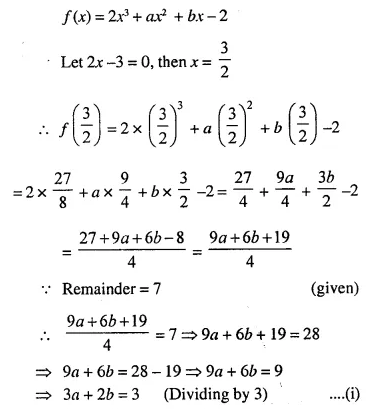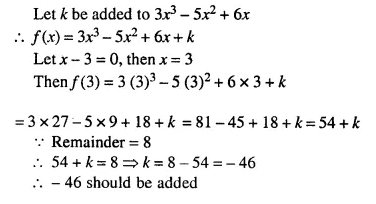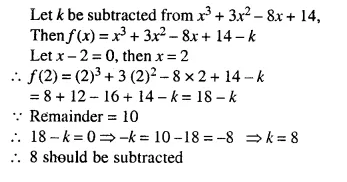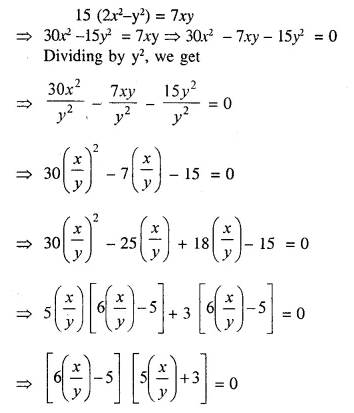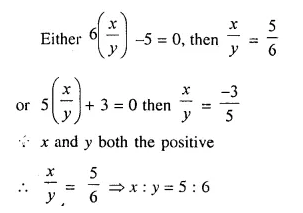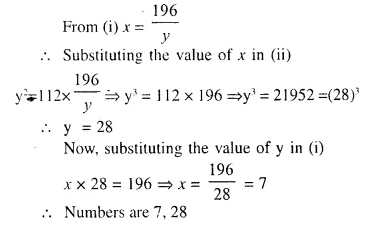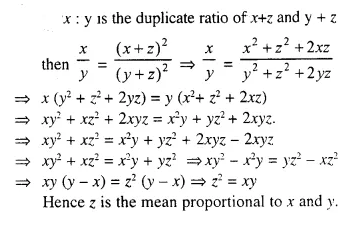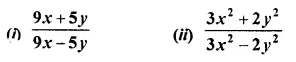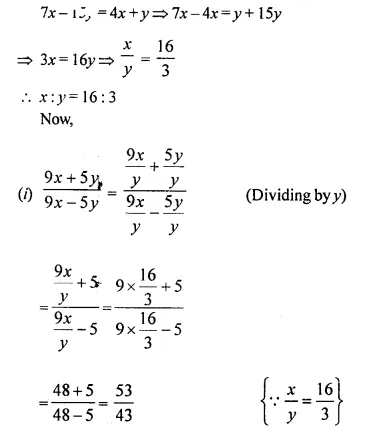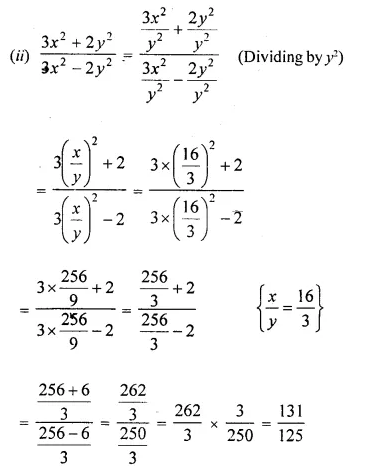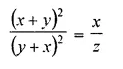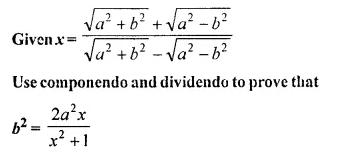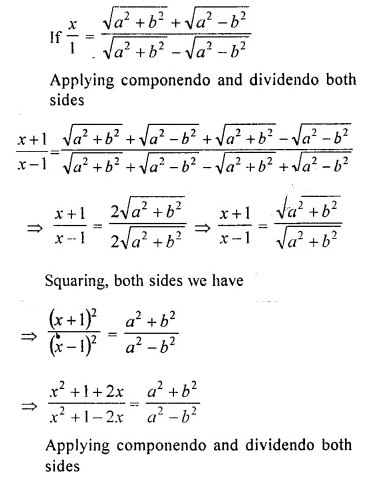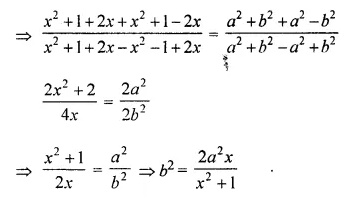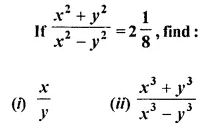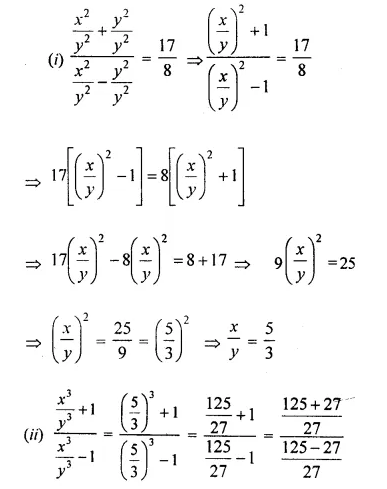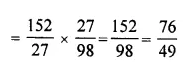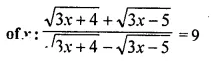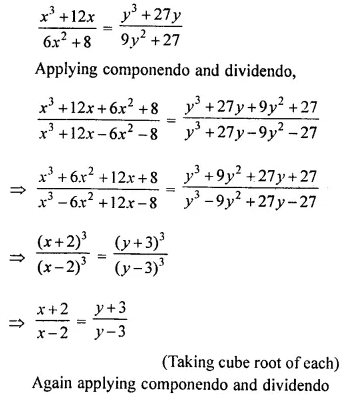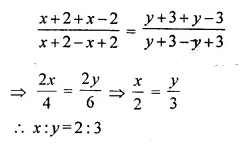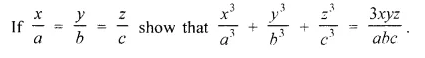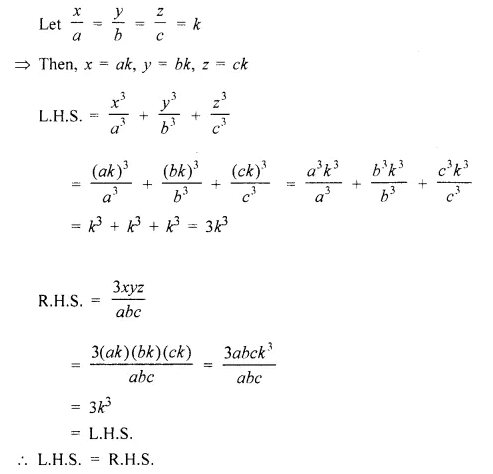Selina Concise Mathematics Class 10 ICSE Solutions Chapter 9 Matrices Ex 9A

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 9 Matrices Ex 9A.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 9 Matrices Ex 9A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 9 Matrices Ex 9B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 9 Matrices Ex 9C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 9 Matrices Ex 9D

Question 1.
State, whether the following statements are true or false. If false, give a reason.
(i) If A and B are two matrices of orders 3 x 2 and 2 x 3 respectively; then their sum A + B is possible,
(ii) The matrices A 2 x3, and B 2 x 3, are conformable for subtraction,
(iii) Transpose of a 2 x 1 matrix is a 2 x 1 matrix,
(iv) Transpose of a square matrix is a square matrix,
(v) A column matrix has many columns and only one row.
Solution:
(i) False, because the orders of both the matrices are not same,
(ii) True,
(iii) False, because transpose of a 2 x 1 matrix is a 1 x 2 matrix,
(iv) True,
(v) False, because it has only one column and may have many rows.

Question 2.

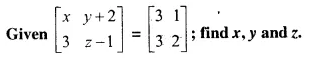
Solution:
Comparing the elements in order, we get that :
x = 3
y + 2 = 1 ⇒ y = 1 – 2 = -1
z – 1 = 2 ⇒ z = 2 + 1 = 3
Hence x = 3, y = -1 , z = 3

Question 3.
Solve for a, b and c; if :

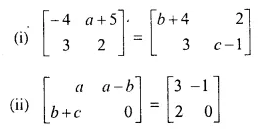
Solution:
(i) Comparing the elements in order, we get
-4 = b + 4 ⇒ – b = 4 + 4 = 8 ⇒ b = – 8
a + 5 = 2 ⇒ a = 2 – 5= -3
2 = c – 1 ⇒ c = 2 + 1 = 3
Hence a = -3, b = -8, c = 3
(ii) Comparing the elements in order, we get
a = 3
a – b = – 1 ⇒ 3 – b = -1 ⇒ -b = -1 – 3 ⇒ -b = -4 ⇒ b = 4
b + c = 2 ⇒ 4 + c = 2 ⇒ c = 2 – 4 = -2
Hence a = 3, b = 4, c = – 2

Question 4.

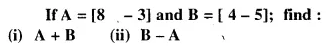
Solution:

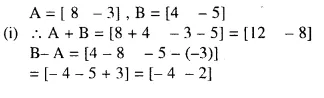
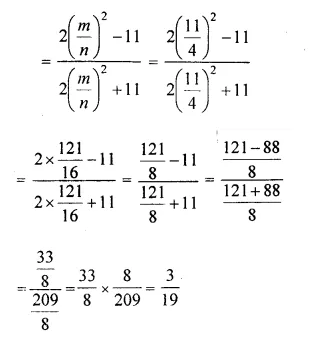
Question 5.

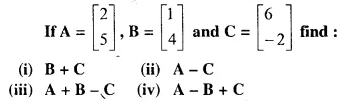
Solution:

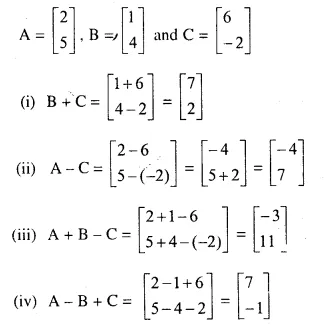
Question 6.
Wherever possible, write each of the following as a single matrix.

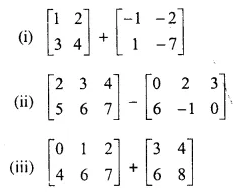
Solution:

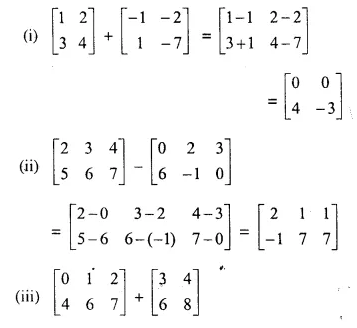
This is not possible because both the matrices are not of the same order.

Question 7.
Find, x and y from the following equations:

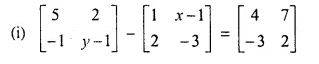
(ii) [-8 x] + [y -2] = [-3 2]
Solution:

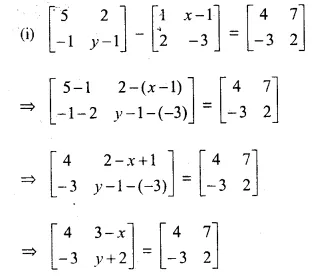
Comparing, the elements of two equal martrices:
3 – x = 7 ⇒ x = -7 + 3 = -4
and y + 2 = 2 ⇒ y = 2 – 2 = 0
Hence x = – 4, y = 0
(ii) [-8 x] + [y -2] = [-3 2]
⇒ [-8 + y x – 2] = [-3 2]
Comparing the elements, we get :
-8 + y = -3 ⇒ y = -3 + 8 = 5
x – 2 = 2 ⇒ x = 2 + 2 = 4
Hence x = 4, y = 5

Question 8.

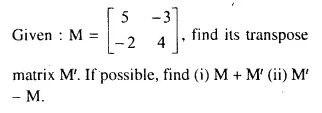
Solution:

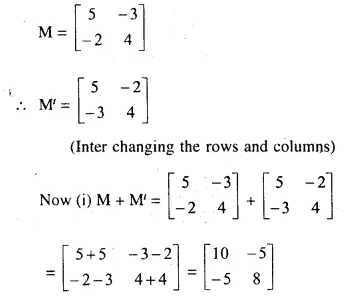
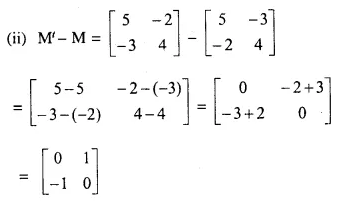
Question 9.
Write the additive inverse of matrices A, B and C

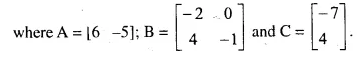
Solution:

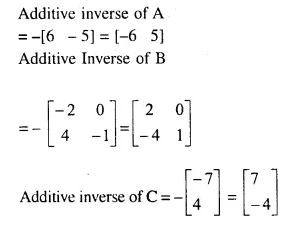
Question 10.
Given A = [ 2 -3], B = [0 2] and C = [-1 4]; find the matrix X in each of the following :
(i) X + B = C – A
(ii) A – X = B + C
Solution:
A = [2 -3], B = [0 2], C = [-1 4]
(i) X + B = C – A
X + [0 2] = [-1 4] – [2 -3]
⇒ X + [0 2] = [- 1 – 2 4 – (-3)]
X + [0 2] = [-3 4 + 3] = [-3 7]
X = [-3 7] – [0 2] = [-3 – 0 7 – 2] = [-3 5]
(ii) A – X = B + C
⇒ -X = B + C – A
⇒ X = A – B – C = [2 -3] – [0 2] – [-1 4] = [2 – 0 – (-1) -3 – 2 – 4] = [ 2 + 1 – 9] = [3 – 9]

Question 11.

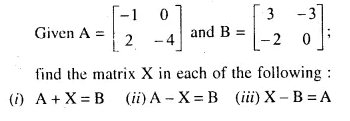
Solution:

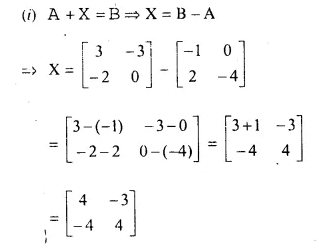
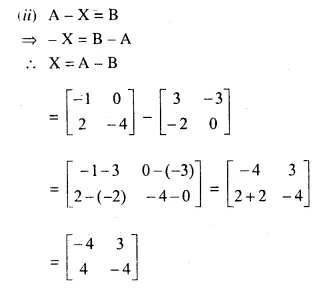
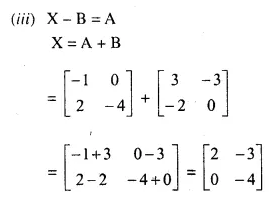
Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 9 Matrices Ex 9A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14E

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14E.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14E

Question 1.
Point P divides the line segment joining the points A (8, 0) and B (16, -8) in the ratio, 3 : 5. Find its co-ordinates of point P. Also, find the equation of the line through P and parallel to 3x + 5y = 7
Solution:

Question 2.
The line segment joining the points A (3, -4) and B (-2, 1) is divided in the ratio 1 : 3 at point P in it Find the co-ordinates of P. Also, find the equation of the line through P and perpendicular to the line 5x – 3y = 4.
Solution:
Point P, divides the line segment A (3, -4) and B(-2, 1) in the ratio of 1 : 3
Let co-ordinates of P be (x, y), then

Question 3.
A line 5x + 3y + 15 = 0 meets y -axis at point P. Find the co-ordinates of point P. Find the equation of a line through P and perpendicular to x – 3y + 4 = 0.
Solution:
P lies on y-axis and let the co-ordinates of P be (0, y)
P lies also on the line 5x + 3y + 15 = 0 it will satisfy it.
5 x 0 + 3y + 15 = 0
⇒ 3y = -15
⇒ y = -5
Co-ordinates of P are (0, -5)
Now, writing the line x – 3y + 4 = 0 is form of y = mx + c
-3y = -x – 4
⇒ 3y = x + 4
⇒ y = \(\frac { 1 }{ 3 }\) x + \(\frac { 4 }{ 3 }\)

Question 4.
Find the value of k for which the lines kx – 5y + 4 = 0 and 5x – 2y + 5 = 0 are perpendicular to each other. [2003]
Solution:
Writing, the line kx – 5y + 4 = 0 in form of y = mx + c
⇒ -5y = -kx – 4
⇒ 5y = kx + 4

Question 5.
A straight line passes through the points P (-1, 4) and Q (5, -2). It intersects the co-ordinate axes at points A and B. M is the mid point of the segment AB. Find:
(i) the equation of the line.
(ii) the co-ordinates of A and B.
(iii) the co-ordinates of M. (2003)

Solution:


(ii) Let. co-ordinates of A be (x, 0) and of B be (0, y) which lie On the line.
Substituting, the co-ordinates in (i)
x + 0 = 3 ⇒x = 3
Co-ordinates of A are (3, 0)
Again 0 + y = 3 ⇒ y = 3
Co-ordinates of B are (0,3)
(iii) M is the mid-point of AB.
Co-ordinates of M wil be (\(\frac { 3 }{ 2 }\) , \(\frac { 3 }{ 2 }\))

Question 6.
(1, 5) and (-3, -1) are the co-ordinates of vertices A and C respectively of rhombus ABCD. Find the equations of the diagonals AC and BD.
Solution:
Co-ordinates of A and C of rhombus ABCD are (1, 5) and (-3, -1)


⇒ 3y – 6 = -2x – 2
⇒ 2x + 3y = 6 – 2
⇒ 2x + 3y = 4

Question 7.
Show that A (3, 2), B (6, -2) and C (2, -5) can be the vertices of a square.
(i) Find the co-ordinates of its fourth vertex D, if ABCD is a square.
(ii) Without using the co-ordinates of vertex D, find the equation of side AD of the square and also the equation of diagonal BD.
Solution:
Three vertices of a square ABCD are A (3, 2), B (6, -2) and C (2, -5)
Let, co-ordinates of fourth vertex D be (x, y)

Question 8.
A line through origin meets the line x = 3y + 2 at right angles at point X. Find the co-ordinates of X.
Solution:
Slope of line x = 3y + 2 or 3y = x – 2 ….(i)

Question 9.
A straight line passes through the point (3, 2) and the portion of this line intercepted between the positive axes, is bisected at this point. Find the equation of the line.
Solution:

Let, the line intersects x-axis at A and y-axis at B.
Let, co-ordinates of A (x, o) and of (o, y)
But (3, 2) is the mid-point of AB.

Question 10.
Find the equation of the line passing through the point of intersection of 7x + 6y = 71 and 5x – 8y = -23; and perpendicular to the line 4x -2y = 1.
Solution:
7x + 6y = 71 ….(i)
5x – 8y = -23 ….(ii)
Multiply (i) by 4 and (ii) by 3,
28x + 24y = 284
15x – 24y = -69
On adding (i) and (ii), we get:
43x = 215
x = 5
Substituting, the value of x in (i)
7 x 5 + 6y = 71
35 + 6y = 71
⇒ 6y = 71 – 35 = 36
⇒ y = 6
Point of intersection of these lines is (5, 6)
Now slope of line 4x – 2y = 1
⇒ 4x – 1 = 2y
⇒ y = 2x – \(\frac { 1 }{ 2 }\) is 2
Slope of line through the point of intersection and perpendicular to 4x – 2y = 1 is \(\frac { -1 }{ 2 }\)
Equation of the line y – y₁ = m (x – x₁)
⇒ y – 6 = \(\frac { -1 }{ 2 }\) (x – 5)
⇒ 2y – 12 = -x + 5
⇒ x + 2y = 5 + 12 = 17
⇒ x + 2y = 17

Question 11.
Find the equation of the line which is perpendicular to the line \(\frac { x }{ a }\) – \(\frac { y }{ b }\) = 1 at the point where this line meets y-axis.
Solution:

Question 12.
O (0, 0), A (3, 5) and B (-5, -3) are the vertices of triangle OAB. Find:
(i) the equation of median of ∆OAB through vertex O.
(ii) the equation of altitude of ∆OAB through vertex B.
Solution:
(i) Let, mid-point of AB be D.

Question 13.
Determine whether the line through points (-2, 3) and (4, 1) is perpendicular to the line 3x = y + 1.
Does line 3x = y + 1 bisect the line segment joining the two given points ?
Solution:
Slope of the line joining the points (-2, 3) and (4, 1)

Yes, these are perpendicular to each other
Let P be the mid-point of the line joining the points (-2, 3) and (4, 1)
Co-ordinates of P will be

This point (1, 2) satisfies the equaion 3x = y + 1 then, it will bisect the line joining the given point
now, substituting the value of x and y. in 3x = y + 1
⇒ 3 x 1 = 2 + 1
⇒ 3 = 3. which is true.
Yes, the line 3x = y + 1 is the bisector.

Question 14.
Given a straight line x cos 30° + y sin 30° = 2. Determine the equation of the other line which is parallel to it and passes through (4, 3).
Solution:
Equation of the given line is x cos 30° + y sin 30° = 2
y sin 36° = -x cos 30° + 2

Question 15.
Find the value of k such that the line (k – 2) x + (k + 3) y – 5 = 0 is :
(i) perpendicular to the line 2x – y + 7 = 0
(ii) parallel to it.
Solution:
Writing the given equation in the form of y = mx + c
(k – 2) x + (k + 3) y – 5 = 0 ….(i)
⇒ (k + 3) y = – (k – 2) x + 5

Question 16.
The vertices of a triangle ABC are A (0, 5), B (-1, -2) and C (11, 7) write down the equation of BC. Find :
(i) the equation of line through A and perpendicular to BC.
(ii) the co-ordinates of the point P, where the perpendicular through A, as obtained in (i) meets BC.
Solution:
Vertices of ∆ABC are A (0, 5),B (-1, -2) and C (11, 7)

(ii) Let, the line through A meets BC in P
P is point of intersection of these two lines.
3x – 4y = 5 ……… (i)
4x + 3y = 15 …….. (ii)
On solving (i), (ii) we get
x = 3, y = 1
Co-ordinates of Pare (3, 1)

Question 17.
From the given figure, find :
(i) the co-ordinates of A, B and C.
(ii) the equation of the line through A and parallel to BC. (2005)

Solution:
(i) From the figure, we see that co-ordinates of A are (2, 3), of B are (-1, 2) of C and (3, 0)
(ii) Slope of line BC is (m)

⇒ x + 2y – 6 – 2 = 0
⇒ x + 2y – 8 = 0
⇒ x + 2y = 8

Question 18.
P (3, 4), Q (7, -2) and R (-2, -1) are the vertices of triangle PQR. Write down the equation of the median of the triangle through R. (2004)
Solution:
Let (x, y) be the co-ordinates of M, the mid-point of PQ.


⇒ x + 2y – 8 = 0
⇒ x + 2y = 8

Question 19.
A (8, -6), B (-4, 2) and C (0, -10) are the vertjces of a triangle ABC. If P is the mid-point of AR and Q is the mid-point of AC, use co ordinate geometry to show that PQ is parallel to BC. Give a special name to quadrilateral PBCQ.
Solution:
In ∆ABC, co-ordinates of A, B and C are (8, -6), (-4, 2) and C (0, -10) respectively.
P and Q are the mid-points of AB and AC respectively
Co-ordinates of P will be


Slopes of PQ and BC are same.
These are parallel to each other.
Quad. PBCQ is trapezium

Question 20.
A line AB meets the x-axis at point A and y-axis at point B. The point P(-4, -2) divides the line segment AB internally such that AP : PB = 1 : 2. Find :
(i) the co-ordinates of A and B.
(ii) equation of line through P, and perpendicular to AB.
Solution:
Line AB intersects x-axis at A and y-axis at B.
(i) Let co-ordinates of A be (x, 0) and of B be (0, y)
Point P (-4, -2) intersects AB in the ratio 1 : 2

Question 21.
A line intersects x-axis at point (-2, 0) and cuts off an intercept of 3 units from die positive side of y-axis. Find the equation of the line. (1992)
Solution:
Let line intersects x-axis at P (-2, 0) and cuts off an intercept of 3 units at Q.

Question 22.
Find the equation of a line passing through the point (2, 3) and having the x-intercept of 4 units. (2002)
Solution:
x-intercept = 4
Co-ordinates of that point = (4, 0)
The co-ordinates of the given point (2, 3)

Question 23.
The given figure (not drawn to scale) shows two straight lines AB and CD. If’ equation of the line AB is : y = x + 1 and equation of line CD is : y = √3 x – 1. Write down the inclination of lines AB and CD; also, find the angle 6 between AB and CD. (1989)

Solution:
Equation of line AB is y = x + 1
and equation of line CD is y = √3 x – 1
Slope of AB = 1
tanθ = 1
⇒ θ = 45°
Inclination angles of AB = 45°
Slope of CD = tanθ = √3 = tan 60°
⇒ θ = 60°
Inclination angle of CD = 60°
In ΔPQR,
Ext. ∠RQX = ∠RPQ + ∠PRQ (Exterior angles is equal to sum of its interior opposite angles)
⇒ 60° = 45° + θ
⇒ θ = 60° – 45° = 15°
⇒ θ = 15°

Question 24.
Write down the equation of the line whose gradient is \(\frac { 3 }{ 2 }\) and which passes through P, where P divides the line segment joining A (-2, 6) and B (3, -4) in the ratio 2 : 3. (1996, 2001)
Solution:
P divides the line segment AB in which A (-2, 6) and B (3, -4) in the ratio 2 : 3
Co-ordinates of P will be

Question 25.
The ordinate of a point lying on the line joining the points (6, 4) and (7, -5) is -23. Find the co-ordinates of that point.
Solution:
Let points are A (6, 4) and B (7, -5)

Question 26.
Points A and B have coordinates (7, -3) and (1, 9) respectively. Find
(i) the slope of AB.
(ii) the equation of the perpendicular bisector of the line segment AB.
(iii) the value of ‘p’ of (-2, p) lies on it.
Solution:
Coordinates of A are (7, -3), of B = ( 1, 9)

Question 27.
A and B are two points on the x-axis and y-axis respectively. P (2, -3) is the mid point of AB. Find the
(i) Coordinates of A and B.
(ii) Slope of line AB.
(iii) equation of line AB.

Solution:
As P (2, -3) is mid-point of AB.
Let coordinates of B be (0, y) and coordinates of A be (x, 0)

Question 28.
The equation of a line is 3x + 4y – 7 = 0. Find:
(i) the slope of the line.
(ii) the equation of a line perpendicular to the given line and passing through the intersection of the lines x – y + 2 = 0 and 3x + y – 10 = 0.
Solution:
Given line 3x + 4y -7 = 0


⇒ 3 (y – 4) = 4 (x – 2)
⇒ 3y – 12 = 4x – 8
⇒ 4x – 3y – 8 + 12 = 0
⇒ 4x – 3y + 4 = 0

Question 29.
ABCD is a parallelogram where A (x, y), B (5, 8), C (4, 7) and D (2, -4). Find :
(i) co-ordinates of A
(ii) equation of diagonal BD.
Solution:

(i) In || gm ABCD, A (x, y), B (5, 8), C (4, 7) and D (2, -4)
The diagonals of ||gm bisect each other
O is said point of AC and BD
Now if O is mid point of BD then its co-ordinates will be


⇒ y + 4 = 4x – 8
⇒ 4x – y -8 – 4 = 0
⇒ 4x – y – 12 = 0 or 4x – y = 12

Question 30.
Given equation of line L₁ is y = 4.
(i) Write the slope of line L₂ if L₂ is the bisector of angle O.
(ii) Write the co-ordinates of point P.
(iii) Find the equation of L₂.
Solution:
(i) Equation of line L₁ is y = 4
L₂ is the bisector of ∠O

Question 31.
Find:

(i) equation of AB
(ii) equation of CD
Solution:
Co-ordinates of A and B are (-5, 4) and (3, 3) respectively.

Question 32.
Find the equation of the line that has x-intercept = -3 and is perpendicular to 3x + 5y = 1
Solution:
x-intercept of the line = -3
and is perpendicular to the line
3x + 5y = 1
5y = 1 – 3x

Question 33.
A straight line passes through the points P (-1, 4) and Q (5, -2). It intersects x-axis at point A and y-axis at point B. M is the mid-point of the line segment AB. Find :
(i) the equation of the line.
(ii) the co-ordinates of points A and B.
(iii) the co-ordinates of point M.
Solution:
A line passing through the two points P (-1, 4) and Q (5, -2) intersects x-axis at point A and y- axis at point B.
M is mid-point of AB

(i) Equation of line AB will be
y – y₁ = m (x – x₁)
⇒ y – 4 = -1 (x + 1)
⇒ y – 4 = – x – 1
⇒ y + x = -1 + 4
⇒ x + y = 3
(ii) The line intersect x-axis at A and OA = 3 units
Co-ordinates of A are (3, 0) and the line intersects y-axis at B and OB = 3 units
Co-ordinates of B are (0, 3)
(iii) M is mid-point of AB
Co-ordinates of M are (\(\frac { 3 }{ 2 }\) , \(\frac { 3 }{ 2 }\))

Question 34.
In the given figure, line AB meets y-axis at point A. Line through C (2, 10) and D intersects line AB at right angle at point P. Find:

(i) equation of line AB.
(ii) equation of line CD.
(iii) co-ordinates of points E and D.
Solution:
In the given figure, AB meets y-axis at point A.
Line through C (2, 10) and D intersects line AB at P at right angle.

Equation of CD
y – 10 = 3 (x – 2)
⇒ y – 10 = 3x – 6
⇒ 3x – y + 10 – 6 = 0
⇒ 3x – y + 4 = 0
(iii) Co-ordinates of D which is on x-axis
3x – y + 4 = 0
3x – 0 + 4 = 0
⇒ 3x + 4 = 0
⇒ 3x = -4
⇒ x = \(\frac { -4 }{ 3 }\)
Co-ordinates of D are (\(\frac { -4 }{ 3 }\) , 0)
E is also on x-axis
x + 3y = 18
Substituting, y = 0, then
x + 0= 18
⇒ x = 18
Co-ordinates of E are (18, 6)

Question 35.
A line through point P (4, 3) meets x-axis at point A and the y-axis at point B. If BP is double of PA, find the equation of AB.
Solution:
A line through P (4, 3) meets x-axis at A and the y-axis at B. If BP is double of PA.
Draw BC || x-axis
and PC || y-axis
In ∆PAD and ∆PBC
∠P = ∠P (common)
∠D = ∠C (each 90°)
∆PAD ~ ∆PBC
PB = 2PA ⇒ PA = \(\frac { 1 }{ 2 }\) PB


2y – 6 = 3x – 12
⇒ 3x – 2y – 12 + 6 = 0
⇒ 3x – 2y – 6 = 0
⇒ 3x – 2y = 6

Question 36.
Find the equation of line through the intersection of lines 2x – y = 1 and 3x + 2y = -9 and making an angle of 30° with positive direction of x-axis.
Solution:
Equation of given two intersecting lines are 2x – y = 1 and 3x + 2y = -9 Which make an angle of 30°

Question 37.
Find the equation of the line through the points A (-1, 3) and B (0, 2). Hence, show that the points A, B and C (1, 1) are collinear.
Solution:
The given points are A (-1, 3) and B (0, 2) and co-ordinates of a point C are (1, 1)
Now slope of the line joining A and B

Equation of the line y – y₁ = m(x – x₁)
⇒ y – 2 = -1 (x – 0)
⇒ y – 2 = -x
⇒ x + y – 2 = 0
Point C (1, 1) will be on AB if it satisfy
1 + 1 – 2 = 0
⇒ 0 = 0
Point C lies on AB
Hence points A, C and B are collinear.

Question 38.
Three vertices of a parallelogram ABCD taken in order are A (3, 6), B (5, 10) and C (3, 2), find:
(i) the co-ordinates of the fourth vertex D.
(ii) length of diagonal BD.
(iii) equation of side AB of the parallelogram ABCD. (2015)
Solution:
Three vertices of a ||gm ABCD taken an order are A (3, 6), B (5, 10) and C (3, 2)
Join diagonals AC and BD which bisect each other at O.
O is mid-point of AC as well as of BD
Now co-ordinates of O will be

Question 39.
In the figure, given, ABC is a triangle and BC is parallel to the y-axis. AB and AC intersect the y-axis at P and Q respectively.

(i) Write the co-ordinates of A.
(ii) Find the length of AB and AC.
(iii) Find the ratio in which Q divides AC.
(iv) Find the equation of the line AC. (2015)
Solution:
In the given figure,
ABC is a triangle and BC || y-axis
AB and AC intersect the y-axis at P and Q respectively.
(i) Co-ordinates of A are (4,0).
(ii) Length of AB

Question 40.
The slope of a line joining P (6, k) and Q (1 – 3k, 3) is \(\frac { 1 }{ 2 }\). Find :
(i) k
(ii) mid-point of PQ, using the value of ‘A’ found in (i). (2016)
Solution:
(i) Slope of the line joining P(6, k) and Q (1 –

Question 41.
A line AB meets X-axis at A and Y-axis at B. P (4, -1) divides AB in the ratio 1 : 2.
(i) Find the coordinates of A and B.
(ii) Find the equation of the line through P and perpendicular to AB.

Solution:
(i) Since, A lies on the x-axis,
let the coordinates of A be (x, 0).
Since B lies on the y-axis,
let the coordinates of B be (0, y).
Let m = 1 and n = 2.
Using section formula,

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14E are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity (With Applications to Maps and Models) Ex 15C

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15C.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15E

Question 1.
(i) The ratio between the corresponding sides of two similar triangles is 2 is to 5. Find the ratio between the areas of these triangles.
(ii) Areas of two similar triangles are 98 sq.cm and 128 sq.cm. Find the ratio between the lengths of their corresponding sides.
Solution:

Question 2.
A line PQ is drawn parallel to the base BC, of ΔABC which meets sides AB and AC at points P and Q respectively. If AP = \(\frac { 1 }{ 3 }\) PB; find the value of:

Solution:

Question 3.
The perimeters of two similar triangles are 30 cm and 24 cm. If one side of first triangle is 12 cm, determine the corresponding side of the second triangle.
Solution:
Let we are given ΔABC and ΔPQR are similar.
Perimeter of ΔABC = 30 cm.
and perimeter of ΔPQR = 24 cm.
and side BC = 12 cm.
Now we have to find the length of QR, the corresponding side of ΔPQR
ΔABC ~ ΔPQR

Question 4.
In the given figure AX : XB = 3 : 5

Find :
(i) the length of BC, if length of XY is 18 cm.
(ii) ratio between the areas of trapezium XBCY and triangle ABC.
Solution:
We are given in the ΔABC, AX : XB = 3 : 5
XY || BC.
Let AX = 3x and XB = 5x
AB = 3x + 5x = 8x.
Now in ΔAXY and ΔABC,
∠AXY = ∠ABC (corresponding angles)
∠A = ∠A (common)
ΔAXY ~ ΔABC (AA Postulate)

Question 5.
ABC is a triangle. PQ is a line segment intersecting AB in P and AC in Q such that PQ || BC and divides triangle ABC into two parts equal in area. Find the value of ratio BP : AB.
Given- In ΔABC, PQ || BC in such away that area APQ = area PQCB
To Find- The ratio of BP : AB

Solution:
In ΔABC, PQ || BC.
Z APQ = Z ABC (corresponding angles)
Now in ΔAPQ and ΔABC,
∠APQ = ∠ABC (proved)
∠A = ∠A (common)
ΔAPQ ~ ΔABC (AA postulate)

Question 6.
In the given triangle PQR, LM is parallel to QR and PM : MR = 3 : 4

Solution:
In ΔPQR, LM || QR in such away that PM : MR = 3 : 4
(i) In ΔPQR, LM || QR

Question 7.
The given diagram shows two isosceles triangles which are similar also. In the given diagram, PQ and BC are not parallel: PC = 4, AQ = 3, QB = 12, BC = 15 and AP = PQ.

Calculate-
(i) the length of AP
(ii) the ratio of the areas of triangle APQ and triangle ABC.
Solution:

Question 8.
In the figure, given below, ABCD is a parallelogram. P is a point on BC such that BP : PC = 1 : 2. DP produced meets AB produced at Q. Given the area of triangle CPQ = 20 cm². Calculate
(i) area of triangle CDP
(ii) area of parallelogram ABCD [1996]

Solution:
(i) Join QC.
In ΔBPQ and ΔCPD,
∠DPC = ∠BPQ (vertically opposite angles.)
∠PDC = ∠BQP (Alternate angles.)
ΔBPQ ~ ΔCDP (AA postulate)

⇒ area ΔCDP = 4 (area ΔBPQ)
⇒ 2 (2 area ΔBPQ) = 2 x 20 = 40 cm² (2 area A BPQ = 20 cm²)
(ii) Area || gm ABCD = area ΔCPD + area ΔADQ – area ΔBPQ
= 40 + 9 (area BPQ) – area BPQ [(AD = CB = 3 BP)]
= 40 + 8 (area ΔBPQ)
= 40 + 8 (10) cm²
= 40 + 80
= 120 cm²

Question 9.
In the given figure. BC is parallel to DE. Area of triangle ABC = 25 cm². Area of trapezium BCED = 24 cm² and DE = 14 cm. Calculate the length of BC. Also. Find the area of triangle BCD.

Solution:
In ΔADE, BC || DE
Area of ΔABC = 25 cm²
and area of trapezium BCED = 24 cm²
Area of ΔADE = 25 + 24 = 49 cm²
DE = 14 cm,
Let BC = x cm.
Now in ΔABC and ΔADE,
∠ABC = ∠ADE (corresponding angles)
∠A = ∠A (common)
ΔABC ~ ΔADE (AA postulate)

Question 10.
The given figure shows a trapezium in which AB is parallel to DC and diagonals AC and BD intersect at point P. If AP : CP = 3 : 5.

Find-
(i) ΔAPB : ΔCPB
(ii) ΔDPC : ΔAPB
(iii) ΔADP : ΔAPB
(iv) ΔAPB : ΔADB
Solution:
AP : CP = 3 : 5 ⇒ \(\frac { AP }{ CP }\) = \(\frac { 3 }{ 5 }\)
(i) Now in ΔAPB and ΔCPB,
These triangles have same vertex and their bases are in the same straight line
area ΔAPB : area ΔCPB = AP : PC = 3 : 5 or ΔAPB : ΔCPB = 3 : 5
(ii) In ΔAPB and ΔDPC,
∠APB = ∠DPC (vertically opposite angles)
∠PAB = ∠PCD (alternate angles)
ΔAPB ~ ΔDPC (AA postulate)

⇒ area ΔDPC : area ΔAPB = 25 : 9 or ΔDPC : ΔAPB = 25 : 9
(iii) In ΔADP and ΔAPB,
There have the same vertex and their bases arc in the same straight line.
area ΔADP : area ΔAPB = DP : PB
But PC : AP = 5 : 3
ΔADP : ΔAPB = 5 : 3
(iv) Similarly area ΔAPB : area ΔADB = PB : DB = 3 : (3 + 5) = 3 : 8

Question 11.
In the given figure, ARC is a triangle. DE is parallel to BC and \(\frac { AD }{ DB }\) = \(\frac { 3 }{ 2 }\).
(i) Determine the ratios \(\frac { AD }{ AB }\) , \(\frac { DE }{ BC }\)
(ii) Prove that ΔDEF is similar to ΔCBF.
Hence, find \(\frac { EF }{ FB }\)
(iii) What is the ratio of the areas of ΔDEF and ΔBFC?

Solution:

Question 12.
In the given figure, ∠B = ∠E, ∠ACD = ∠BCE, AB = 10.4 cm and DE = 7.8 cm. Find the ratio between areas of the ΔABC and ΔDEC.

Solution:
In the figure DE = 7.8 cm, AB = 10.4 cm
∠ACD = ∠BCE (given)
Adding ∠DCB both sides,
∠ACD + ∠DCB = ∠DCB + ∠BCE
∠ACB = ∠DCE
Now in ΔABC and ΔDCE
∠B = ∠E (given)
∠ACB = ∠DCE (proved)
ΔABC ~ ΔDCE (AA axiom)

Question 13.
Triangle ABC is an isosceles triangle in which AB = AC = 13 cm and BC = 10 cm. AD is perpendicular to BC. If CE = 8 cm and EF ⊥ AB, find:

Solution:
In the figure, ΔABC is an isosceles triangle in which
AB = AC = 13 cm, BC = 10 cm,
AD ⊥ BC, CE = 8 cm and EF ⊥ AB
(i) Now in ΔADC and ΔFEB
∠C = ∠B (AB = AC)
∠ADC = ∠EFB (each = 90°)
ΔADC ~ ΔFEB (AA axiom)

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 15 Similarity Ex 15C are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Chapter 21 Trigonometrical Identities (Including Trigonometrical Ratios of Complementary Angles and Use of Four Figure Trigonometrical Tables) Ex 21D

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21D.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21E

Question 1.
Use tables to find sine of:
(i) 21°
(ii) 34°42′
(iii) 47° 32′                    
(iv) 62°57′
(v) 10°20′ + 20° 45′
Solution:
From tables of sine of angles, we find that:
(i) sin 21°= 0.3584,
(ii) sin 34°42’= .5693
(iii) sin 47° 32′ = 0.7377
(iv) sin 62° 57′ = 0.8906
(v) sin 10° 20′ + 20°45′ = sin 31°5′
= 0.5162

Question 2.
Use tables to find cosine of:
(i) 2°4′
(ii) 8°12′
(iii) 26°32’                     
(iv) 65°41′
(v) 9°23′ +15°54′
Solution:
From tables of cosine of angle, we find that:
(i) cos 2°4′ = 0.9993
(ii) cos 8° 12’ = 0.9898
(iii) cos 26°32′ = 0.8946
(iv) cos 65°41′ = 0.4118
(v) cos 9°23′ + 15°54′ = cos 25° 17′
= 0.9042

Question 3.
Use trigonometrical tables to find tangent of:
(i) 37°
(ii) 42°18′
(iii) 17°27′
Solution:
From the tables of tangents, we find that
(i) tan 35° = 0.7536
(ii) tan 42°18’= 0.9099
(iii) tan 17°27’= 0.3144

Question 4.
Use tables to find the acute angle θ, if the value of sin θ
(i) 4848
(ii) 0.3827
(iii) 0.6525
Solution:
From the tables of series, we find that of :
(i) sinθ = 0.4848, then θ = 29°
(ii) sinθ = 0.3827, then θ = 20° 30′
(iii) sin θ = 0.6525, then θ = 40° 42’ + 2′ = 40°44′

Question 5.
Use tables to find the acute angle θ, if the value of cos θ is :
(i) 0.9848
(ii) 0.9574
(iii) 0.6885
Solution:
From the tables of cosines, we find that if :
(i) cos θ = 0.9848, then θ = 10°
(ii) cos θ = 0.9574, then θ = 16°48′- 1’=16°47’
(iii) cos θ = 0.6885, then θ = 46° 30′ or 46°30′
= 46° 29’

Question 6.
Use tables to find the acute angle θ, if the value of tan θ is :
(i) 2419
(ii) 0.4741
(iii) 0.7391                     
(iv) 1.06
Solution:
From the table of tangents, we find that if:
(i) tan θ = 0.2419, then θ=13° 36’
(ii) tan θ = 0.4741, then θ = 25° 18’ + 4’ = 25°22′
(iii) tan θ = 0.7391, then θ= 36°24’+ 4′ = 36°28′
(iv) tan θ = 1.06, then θ = 46°36′ + 4′ = 46°40′

Question 7.
If sin θ=0.857; find:
(i) θ                              
(ii) tan θ
Solution:
From the tables of T. Ratio’s we find this :
(i) If sin θ = 0.857, then θ = 58°54′ + 4.5′ = 58° 58′ or 58°59’
(ii) tan 58°58’= 1.6577 +43 = 1.662 or tan 58° 59′ = 1.6577 + 53 = 1.663

Question 8.
If θ is the acute angle and cos θ = 0.7258; find:
(i) θ
(ii) 2 tan θ – sin θ
Solution:
From the tables of T-ratio’s, we find that:
(i) If cos θ = 0.7258, then θ= 43° 30′ -2′ = 43°28’
(ii) Now 2 tan θ – sin θ= 2 tan 43°28′ – sin 43°28′
2 tan 43°28’ = 2 x (0.9457 + 0.0022)
= 0:9479 x 2 = 1.8958
and sin 43°28′ = 0.6871 + 0.0008 = 0.6879
∴ 2 tan 43°28′ – sin 43° 28′ = 1.8958 – 0.6879 = 1.2079

Question 9.
Let θ be an acute angle and tan θ = 0.9490 find:
(i) θ
(ii) cos θ
(iii) sin θ – cos θ
Solution:
From the tables of T-raios, we find that:
(i) if tan θ = 0.9490 , then θ = 43°30′
(ii) cos θ = cos 43°30′ = 0.7254
(iii) sin θ = sin 43°50′ = 0.6884
∴ sin θ – cos θ = 0.6884 – 0.7254 = -0.0370 = -0.037

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 21 Trigonometrical Identities Ex 21D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14D

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14D.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14D
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14E

Question 1.
Find the slope and y-intercept of the line :
(i) y = 4
(ii) ax – by = 0
(iii) 3x – 4y = 5
Solution:
(i) y = 4 ⇒ y = 0x + 4
Here slope = 0 and y-intercept = 4
(ii) ax – by = 0
⇒ by = ax
⇒ y = \(\frac { a }{ b }\) x + 0
Here, slope = \(\frac { a }{ b }\) and y-intercept = 0
(iii) 3x – 4y = 5
⇒ – 4y = 5 – 3x
⇒ 4y = 3x – 5
⇒ y = \(\frac { 3 }{ 4 }\) x + \(\frac { -5 }{ 4 }\)
Here, slope = \(\frac { 3 }{ 4 }\) and y- intercept = \(\frac { -5 }{ 4 }\)

Question 2.
The equation of a line is x – y = 4. Find its – slope and y-intercept. Also, find its inclination.
Solution:
x – y = 4
writing the equation in form of y = mx + c
x = 4 + y
⇒ y = x – 4
Slope = 1 and y-intercept = – 4
Slope = 1
⇒ tanθ = 1
⇒ θ = 45°

Question 3.
(i) Is the line 3x + 4y + 7 = 0 perpendicular to the line 28x – 21y + 50 = 0 ?
(ii) Is the line x – 3y = 4 perpendicular to the line 3x – y = 7 ?
(iii) Is the line 3x + 2y = 5 parallel to the line x + 2y = 1 ?
(iv) Determine x so that the slope of the line through (1, 4) and (x, 2) is 2.
Solution:
(i) 3x + 4y + 7 = 0
Writing the equation in form of y = mx + c
4y = -3x – 7

Question 4.
Find the slope of the line which is parallel to:
(i) x + 2y + 3 = 0
(ii) \(\frac { x }{ 2 }\) – \(\frac { y }{ 3 }\) – 1 = 0
Solution:

Question 5.
Find the slope of the line which is perpendicular to:
(i) x – \(\frac { y }{ 2 }\) + 3 = 0
(ii) \(\frac { x }{ 3 }\) – 2y = 4
Solution:

Question 6.
(i) Lines 2x – by + 5 = 0 and ax + 3y = 2 are parallel to each other. Find the relation connecting a and b.
(ii) Lines mx + 3y + 7 = 0 and 5x- ny – 3 = 0 are perpendicular to each other. Find the relation connecting m and n.
Solution:
(i) Writing the given equations in the form of y = mx + c, we get:
-by = -2x -5
by = 2x + 5

Question 7.
Find the value of p if the lines, whose equations are 2x – y + 5 = 0 and px + 3y = 4 are perpendicular to each other.
Solution:
Writing the given equations 2x – y + 5 = 0 and px + 3y = 4 in form of y = mx + c
2x – y + 5 = 0
-y = -2x -5
y = 2x + 5
Here, slope of the line = 2
Again, px + 3y = 4
3y = – px + 4

Question 8.
The equation of a line AB is 2x – 2y + 3 = 0.
(i) Find the slope of the line AB.
(ii) Calculate the angle that the line AB makes with the positive direction of the x-axis.
Solution:
The line AB is given.2* – 2y + 3 = 0
Writing it in the form of y = mx + c
-2y = -2x – 3
⇒ 2y = 2x + 3
⇒ y = x + \(\frac { 3 }{ 2 }\)
Here, slope of the line = 1
Angle of inclination = tanθ
tanθ = 1
θ = 45°

Question 9.
The lines represented by 4x + 3y = 9 and px – 6y + 3 = 0 are parallel. Find the value of p.
Solution:
Writing the given lines 4x + 3y = 9 and px – 6y + 3 = 0 in the form of y = mx + c
4x + 3y = 9
⇒ 3y = – 4x + 9

Question 10.
If the lines y = 3x + 7 and 2y +px = 3 are perpendicular to each other, find the value of p. (2006)
Solution:

Question 11.
The line through A (-2, 3) and B (4, 6) is perpendicular to the line 2x – 4y = 5. Find the value of b.
Solution:
Gradient (mx) of the line passing through the points A (-2, 3) and B (4, b)

Question 12.
Find the equation of the line passing through (-5, 7) and parallel to
(i) x-axis
(ii) y-axis.
Solution:
(i) Slope of the line parallel to x-axis = 0
Equation of line passing through (-5, 7) whose slope is 0.
y – 7 = 0 [x – (-5)]
⇒ y – 7 = 0
⇒ y = 7
(ii) Slope of the line parallel to y-axis = 0
y – y1 = m (x – x1)
⇒ 0 = x – x1
⇒ x + 5 = 0

Question 13.
(i) Find the equation of the line passing through (5, -3) and parallel to x – 3y = 4.
(ii) Find the equation of the line parallel to the line 3x + 2y = 8 and passing through the point (0, 1). (2007)
Solution:
(i) Writing the equation x – 3y = 4 in form of y = mx + c
-3y = -x + 4


⇒ 2y – 2 = -3x
⇒ 3x + 2y – 2 = 0
Which is the required equation.

Question 14.
Find the equation of the line passing through (-2, 1) and perpendicular to 4x + 5y = 6.
Solution:
Writing the equation 4x + 5y = 6 in form of y = mx + c

Question 15.
Find the equation of the perpendicular bisector of the line segment obtained on joining the points (6, -3) and (0, 3).
Solution:
The perpendicular of the line segment bisects it.
Co-ordinates of mid-point of the line segment which is obtained by joining the points (6, -3) and (0, 3)

Slope of the line perpendicular to it = 1 (Product of slopes = -1)
Equation of the perpendicular bisector is y – y1 = m (x – x1)
y – 0 = 1 (x – 3)
y = x – 3

Question 16.
In the following diagram, write down:
(i) the co-ordinates of the points A, Band C.
(ii) the equation of the line through A and parallel to BC.

Solution:
(i) From the figure, the see that co-ordinates of A are (2, 3), B are (-1, 2) and C are (3, 0)

Question 17.
B (-5, 6) and D (1, 4) are the vertices of rhombus ABCD. Find the equation of diagonal BD and of diagonal AC.
Solution:

Question 18.
A = (7, -2) and C = (-1, – 6) are the vertices of a square ABCD. Find the equation of the diagonals AC and BD.
Solution:

Question 19.
A (1, -5), B (2, 2) and C (-2, 4) are the vertices of the ∆ABC, find the equation of:
(i) the median of the triangle through A.
(ii) the altitude of the triangle through B.
(iii) the line through C and parallel to AB.
Solution:
(i) Let D be the mid-point of BC
co-ordinates mid-point of

Question 20.
(i) Write down the equation of the line AB, through (3, 2) and perpendicular to the line 2y = 3x + 5.
(ii) AB meets the x-axis at A and the y-axis at B. Write down the co-ordinates of A and B. Calculate the area of triangle OAB, where O is the origin. [1995]
Solution:
(i) Write the equation 2y = 3x + 5 in the form of y = mx + c. We get:

y – 2 = \(\frac { -2 }{ 3 }\) (x – 3)
⇒ 3y – 6 = -2x + 6
⇒ 2x + 3y = 6 + 6
⇒ 2x + 3y = 12 …… (i)
(ii) AB meets the x-axis at A
ordinate (y) of A = 0 i.e. y = 0
Substituting, the value of y in (i)
2x + 3 x 0 = 12
⇒ 2x = 12
⇒ x = 6
Co-ordinates of A are (6, 0)
Again. AB meets y-axis at B
Abscissa of B = 0 i.e. x = 0
Substituting the value of x in (i)
2 x 0 + 3y = 12
⇒ y = 4
Co-ordinates of B are (0, 4)
Area of ∆OAB = \(\frac { 1 }{ 2 }\) x Base x altitude
= \(\frac { 1 }{ 2 }\) x 4 x 6 = 12 square units

Question 21.
The line 4x – 3y + 12 = 0 meets the x-axis at A. Write the co-ordinates of A.
Determine the equation of the line through A and perpendicular to 4x – 3y + 12 = 0.
Solution:
The line 4x – 3y + 12 = 0 meets x-axis at A.
Ordinates of A = 0. i.e. y = 0
Substituting, the value of y in the equation
4x – 3 x 0 + 12 = 0
⇒ 4x + 12 = 0
⇒ 4x = -12
⇒ x = -3
Co-ordinates of A are (-3, 0)
Writing the equation 4x – 3y + 12 = 0 in form of y = mx + c
⇒ -3y = -4x – 12

Question 22.
The point P is the foot of perpendicular from A (-5, 7) to the line is 2x – 3y + 18 = 0. Determine:
(i) the equation of the line AP.
(ii) the co-ordinates of P.
Solution:
Write the equation in form of y = mx + c
2x – 3y + 18 = 0
⇒ -3y = -2x – 18
⇒ y = \(\frac { 2 }{ 3 }\) x + 6 (Dividing by 3)
Slope of the line = \(\frac { 2 }{ 3 }\)
and slope of the line perpendicular to it = \(\frac { -3 }{ 2 }\) (Product of slopes = -1)
(i) Equation of line AP perpendicular to the given line and drawn through A (-5, 7)

y – y1 = m (x – x1)
⇒ y – 7 = \(\frac { -3 }{ 2 }\) (x + 5)
⇒ 2y – 14 = -3x – 15
⇒ 3x + 2y – 14 + 15 = 0
⇒ 3x + 2y + 1 = 0
(ii) P is the point of intersection of these lines
we will solve their equations
2x – 3y + 18 = 0 ….(i)
3x + 2y + 1 = 0 ….(ii)
Multiplying (i) by 2 and (ii) by 3, we get
4x – 6y + 36 = 0
9x + 6y + 3 = 0
Adding, we get:
13x + 39 = 0
⇒ 13x = -39
⇒ x = -3
Now, substituting the value of x in (i)
2(-3) – 3y + 18 = 0
⇒ -6 – 3y + 18 = 0
⇒ -3y + 18 – 6 = 0
⇒ -3y + 12 = 0
⇒ -3y = -12
⇒ 3y = 12
⇒ y = 4
Co-ordinates of P are (-3, 4)

Question 23.
The points A, B and C are (4, 0), (2, 2) and (0, 6) respectively. Find the equations of AB and BC. If AB cuts the y-axis at P and BC cuts the x-axis at Q, find the co-ordinates of P and Q.
Solution:

AB meets y- axis at P
abscissa of P = 0 i. e. x = 0
Substituting the value of y in (i)
0 + y = 4
⇒ y = 4
Co-ordinates of P are (0, 4)
BC meets x-axis at Q
ordinate of Q = 0 i.e. y = 0
Substituting, the value of y in (ii),
2x + 0 = 6
⇒ 2x = 6
⇒ x = 3
Co-ordinates of Q are (3, 0)

Question 24.
Match the equations A, B, C, and D with the lines L1, L2, L3 and L4, whose graphs are roughly drawn in the given diagram.
A = y = 2x;
B = y – 2x + 2 = 0;
C = 3x + 2y = 6;
D = y = 2 [1996]

Solution:
A → L3,
B → L4,
C → L2,
D → L1

Question 25.
Find the value of ‘a’ for which the following points A (a, 3), B (2, 1) and C (5, a) are collinear. Hence find the equation of the line. (2014)
Solution:
A (a, 3), B (2,1) and C (5, a) are collinear.
Slope of AB = Slope of BC

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 14 Equation of a Line Ex 14D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 13 Section and Mid-Point Formula Ex 13A

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 13 Section and Mid-Point Formula Ex 13A.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 13 Section and Mid-Point Formula Ex 13A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 13 Section and Mid-Point Formula Ex 13B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 13 Section and Mid-Point Formula Ex 13C

Question 1.
Calculate the co-ordinates-of the point P which divides the line segment joining:
(i) A (1, 3) and B (5, 9) in the ratio 1 : 2
(ii) A (-4, 6) and B (3, -5) in the ratio 3 : 2
Solution:
(i) Let co-ordinates of P be (x,y)

Question 2.
In what ratio is the line joining (2, -3) and (5, 6) divided by the x-axis ?
Solution:
Let the point P (x, 0) divides in the ratio of m₁ : m₂ line joining the points A (2, -3) and B (5, 6)

Question 3.
In what ratio is the line joining (2, -4) and (-3, 6) divided by the y-axis ?
Solution:
Let the point P (0, y) divides the line joining the points A (2, -4) and (-3, 6) in the ratio of m₁ : m₂

Question 4.
In what ratio does the point (1, a) divide the join of (-1, 4) and (4, -1)? Also, find the value of ‘a’.
Solution:
Let the point P (1, a) divides the line joining the points (-1, 4) and (4, -1) in the ratio of m₁ : m₂

Question 5.
In what ratio does the point (a, 6) divide the join of (-4, 3) and (2, 8) ? Also, find the value of ‘a’.
Solution:
Let the point P (a, 6) divides the line joining the points A (-4, 3), B (2, 8) in the ratio of m₁ : m₂

Question 6.
In what ratio is the join of (4, 3) and (2, -6) divided by the x-axis. Also, find the co-ordinates of the point of intersection.
Solution:

Question 7.
Find the ratio in which the join of (-4, 7) and (3, 0) is divided by the y-axis. Also, find the co-ordinates of the point of intersection.
Solution:
Let, the points (0, y) be the point of intersection which divides the line joining the points A (-4, 7) and B (3, 0)

Question 8.
Points A, B, C and D divide the line segment joining the point (5, -10) and the origin in five equal parts. Find the co-ordinates of A, B, C and D.
Solution:
Points A, B, C and D divide the line segment joining the points (5, -10) and origin (0, 0) in five equal parts
Let co-ordinates of A be (x, y) which divides PO in the ratio of 1 : 4

Question 9.
The line joining the points A (-3, -10) and B (-2, 6) is divided by the point P such that = \(\frac { PA }{ PB }\) = \(\frac { 1 }{ 5 }\), find the co-ordinates of P.
Solution:
Let the co-ordinates of P be (x, y) which divides the line joining the points A (-3,-10) and B (-2,6) in the ratio of AP : PB i.e. (5 – 1) : 1 or 4 : 1

Question 10.
P is a point on the line joining A (4, 3) and B (-2, 6) such that 5AP = 2BP. Find the co-ordinates of P.
Solution:

Question 11.
Calculate the ratio in which the line joining the points (-3, -1) and (5, 7) is divided by the line x = 2. Also, find the co-ordinates of the point of intersection.
Solution:
Let the point P (2, y) divides the line joining the points A (-3, -1) and B (5, 7) in the ratio of m₁ : m₂

Question 12.
Calculate the ratio in which the line joining A (6, 5) and B (4, -3) is divided by the line y = 2.
Solution:
Let the point P (x, 2) divides the line joining the points A (6, 5) and B (4, -3) in the ratio of m₁ : m₂

Question 13.
The point P(5, -4) divides the line segment AB, as shown in the figure, in the ratio 2 : 5. Find the co-ordinates of points A and B.

Solution:
From the figure, the line AB intersects x-axis at A and y-axis at B.
Let the co-ordinates of A (x, 0) and B (0, y) and P (5, -4) divides it in the ratio of 2 : 5

Question 14.
Find the co-ordinates of the points of trisection of the line joining the points (-3, 0) and (6, 6).
Solution:

Question 15.
Show that the line segment joining the points (-5, 8) and (10, -4) is trisected by the co-ordinate axes.
Solution:

Let the points A (-5, 8) and B (10, -4).
Let P and Q be the two points on the axis which trisect the line joining the points A and B.
AP = PQ = QB
AP : PB = 1 : 2 and AQ : QB = 2 : 1

Question 16.
Show that A (3, -2) is a point of trisection of the line-segment joining the points (2, 1) and (5, -8). Also, find the co-ordinates of the other point of trisection.
Solution:

Let A and B are the points of trisection of the line segment joining the points P (2, 1) and Q (5, -8), then
PA = AB = BQ.
PA : AQ = 1 : 2 and PB : BQ = 2 : 1

Question 17.
If A = (-4, 3) and B = (8, -6)
(i) find the length of AB
(ii) In what ratio is the line joining A and B, divided by the x-axis ?
Solution:

Question 18.
The line segment joining the points M (5, 7) and N (-3, 2) is intersected by the y-axis at point L. Write down the abscissa of L. Hence, find the ratio in which L divides MN. Also, find the co-ordinates of L.
Solution:

Question 19.
A (2, 5), B (-1, 2) and C (5, 8) are the co-ordinates of the vertices of the triangle ABC. Points P and Q lie on AB and AC respectively, such that:
AP : PB = AQ : QC = 1 : 2.
(i) Calculate the co-ordinates of P and Q.
(ii) Show that PQ = \(\frac { 1 }{ 3 }\) BC.
Solution:

Question 20.
A (-3, 4), B ( 3, -1) and C (-2, 4) are the vertices of a triangle ABC. Find the length of line segment AP, where point P lies inside BC, such that BP: PC = 2 : 3.
Solution:

Question 21.
ThelinesegmentjoiningA(2, 3)andB(6, -5) is intercepted by x-axis at the point K. Write down the ordinate of the point K. Hence, find the ratio in which K divides AB. Also, find the co-ordinates of the pointK. [1990, 2006]
Solution:
Let the line segment Intersect the x-axis at the point P
Co-ordinates of P are (x, 0)
Let P divide the line segment in the ratio K : 1 then

Question 22.
The line segment joining A (4, 7) and B (-6, -2) is intercepted by the y-axis at the point K. Write down the abscissa of the point K. Hence, find the ratio in which K divides AB. Also, find the co-ordinates of the point K.
Solution:
Points A (4, -7), B (-6, -2) are joined which intersects y-axis at K. abscissa of K will be 0

Let the coordinates of K be (0, y) and K divides AB line segment in the ratio m₁ : m₂

Question 23.
The line joining P (-4, 5) and Q (3, 2), intersects they axis at point R. PM and QN are perpendiculars from P and Q on the x-axis. Find:
(i) The ratio PR: RQ.
(ii) The co-ordinates of R.
(iii) The areas of the quadrilateral PMNQ. [2004]
Solution:
(i) Let divides the line joining the points P (-4, 5) and Q (3, 2) in the ratio k : 1

Question 24.
In the given figure, line APB meets the x- axis at point A and y-axis at point B. P is the point (-4, 2) and AP : PB = 1 : 2. Find the co-ordinates of A and B.

Solution:
Let the co-ordinates of A be (x1, 0) (as it lies on x-axis)
and co-ordinates of B be (0, y2)
and co-ordinates of P are (-4, 2)
AP : PB = 1 : 2 i.e. m1 = 1, m2 = 2
Now, P divides AB in the ratio m₁ : m₂ or 1 : 2

Question 25.
Given a line segment AB joining the points A (-4, 6) and B (8, -3). Find:
(i) the ratio in which AB is divided by the y-axis.
(ii) find the coordinates of the point of intersection.
(iii) the length of AB.
Solution:
(i) Let the y-axis divide AB in the ratio m : 1

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 13 Section and Mid-Point Formula Ex 13A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 23 Graphical Representation (Histograms, Frequency Polygon and Ogives) Ex 23

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Chapter 23 Graphical Representation (Histograms, Frequency Polygon and Ogives) Ex 23.

Question 1.
Draw histograms for the following distributions :

Solution:

Question 2.
Draw a cumulative frequency curve (ogive) for each of the following distributions

Solution:

Question 3.
Draw an ogive for each of the following distributions :

Solution:

Now plotting the points (10, 8), (20, 25), (30, 38), (40, 50) and (50, 67) on the graph and join them with free hand to obtain an ogive as shown in the graph.

Now plot the points (10, 0), (20, 17), (30, 32), (40, 37), (50, 53), (60, 58) and (70, 65) on the graph and join them with free hand to get an ogive as shown in the graph.

Question 4.
Construct a frequency distribution table for the numbers given below, using the class intervals 21-30,31-40…. etc.
75, 67, 57, 50, 26, 33, 44, 58, 67,75, 78, 43, 41, 31, 21, 32, 40, 62, 54, 69, 48, 47,51,38, 39,43,61, 63, 68, 53, 56, 49, 59, 37, 40, 68, 23, 28, 36 and 47.
Use the table obtained to draw:
(i) a histogram
(ii) an ogive
Solution:



(ii) Ogive :
We plot the points (30, 4), (40, 13), (50, 22), (60, 29); (70, 37) and (80, 40) on the graph and join them in free hand to obtain an ogive.

Question 5.
(a) Use the information given in the adjoining histogram to c construct a f frequency table.
(b)Use this table to construct an ogive.

Solution:
From the histogram given, the required frequency table will be as given below.

Plot the points (12, 9), (16, 25), (20, 47), (24, 65), (28, 77), (32, 81) on the graph and join them with free hand to get an ogive as shown.

Question 6.

(a) From the distribution given above, construct a frequency table, (b) Use the table obtained in part (a) to draw :
(i) a histogram
(ii) an ogive.
Solution:
Difference in consecutive class marks. = 17.5 – 12.5 = 5
∴ first class interval will be : 10-15 and so on

(ii) We plot the point (15. 12), (20. 29), (25. 51), (30, 78). (35, 108), (40. 129) and (45, 145) on the graph and join them in free hand to obtain the ogive.

Question 7.
Use graph paper for this question.
The table given beiow shows the monthly wages of some factory workers.
(i) Using the table calculate the cumulative frequencies of workers.
(ii) Draw the cumulative frequency curve.
Use 2 cm = Rs. 500, starting the origin at Rs. 6500 on x-axis, and 2 cm = 10 workers on the y-axis

Solution:


(ii) We plot the points (7000, 10), (7500, 28), (8000, 50), (8500, 75), (9000, 92) (9500, 102) and (10000, 110) on the graph and join them in free hand to obtain an ogive.

Question 8.
The following table shows the distribution of the heights of a group of factory workers :

(i) Determine the cumulative frequencies.
(ii) Draw the ‘less than’ cumulative frequency curve on a graph paper. Use 2 cm = 5cm height on one axis and 2 cm = 10 workers on the other.
Solution:


We plot points (155, 6), (160, 18), (165, 36),
(170, 56), (175, 69), (180, 77) and (185, 83) on the graph and join them in free hand to obtain an ogive.

Question 9.
Construct a frequency distribution table for each of the following distributions :

Solution:

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 23 Graphical Representation Ex 23  are helpful to you.

If you have any doubts, please comment below. We try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 8 Remainder and Factor Theorems Ex 8B

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 8 Remainder and Factor Theorems Ex 8B.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 8 Remainder and Factor Theorems Ex 8A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 8 Remainder and Factor Theorems Ex 8B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 8 Remainder and Factor Theorems Ex 8C

Question 1.
Using the Factor Theorem, show that:
(i) (x – 2) is a factor of x³ – 2x² – 9x +18. Hence, factorise the expression x³ – 2x² – 9x + 18 completely.
(ii) (x + 5) is a factor of 2x³ + 5x² – 28x – 15. Hence, factorise the expression 2x³ + 5x² – 28x – 15 completely.
(iii) (3x + 2) is a factor of 3x³ + 2x² – 3x – 2. Hence, factorise the expression 3x³ + 2x² – 3x – 2. completely.
(iv) 2x + 7 is a factor of 2x³ + 5x² – 11x – 14. Hence, factorise the given expression completely.
Solution:

Question 2.
Using the Remainder Theorem, factorise each of the following completely:
(i) 3x³ + 2x² – 19x + 6
(ii) 2x³ + x² – 13x + 6
(iii) 3x³ + 2x² – 23x – 30
(iv) 4x³ + 7x² – 36x – 63
(v) x³ + x² – 4x – 4. (2004)
Solution:

Question 3.
Using the Remainder Theorem factorise the expression 3x³ + 10x² + x – 6. Hence, solve the equation. 3x³ + 10x² + x – 6 = 0
Solution:

Question 4.
Factorise the expression f(x) = 2x³ – 7x² – 3x + 18. Hence, find all possible values of x for which f(x) = o.
Solution:

Question 5.
Given that x – 2 and x +1 are factors of f(x) = x³ + 3x² + ax + b; calculate the values of a and b. Hence, find all the factors of f(x).
Solution:

Question 6.
The expression 4x³ – bx² + x – c leaves remainders 0 and 30 when divided by x + 1 and 2x – 3 respectively. Calculate the values of b and c. Hence, factorise the expression completely.
Solution:

Question 7.
If x + a is a common factor of expressions f(x) = x² + px + q and g (x) = x² + mx + n show that a = \(\frac { n – q }{ m – p }\)
Solution:

Question 8.
The polynomials ax³ + 3x² – 3 and 2x³ – 5x + a, when divided by x – 4, leave the same remainder in each case. Find the value of a.
Solution:

Question 9.
Find the value of ‘a’ if (x – a) is a factor of x³ – ax² + x + 2.
Solution:

Question 10.
Find the number that must be subtracted from the polynomial 3y³ + y² – 22y + 15, so that the resulting polynomial is completely divisible by y + 3.
Solution:

⇒ 9 – k = 0 ⇒ k = 9
Hence 9 should be subtracted.

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 8 Remainder and Factor Theorems Ex 8B are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 8 Remainder and Factor Theorems Ex 8A

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 8 Remainder and Factor Theorems Ex 8A.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 8 Remainder and Factor Theorems Ex 8A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 8 Remainder and Factor Theorems Ex 8B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 8 Remainder and Factor Theorems Ex 8C

Question 1.
Find in each case, the remainder when :
(i) x⁴ – 3x² + 2x + 1 is divided by x – 1.
(ii) x³ + 3x² – 12x + 4 is divided by x – 2.
(iii) x⁴ + 1 is divided by x + 1.
(iv) 4x³ – 3x² + 2x – 4 is divided by 2x + 1.
(v) 4x³ + 4x² – 21x + 16 is divided by 2x – 3.
(vi) 2x³ + 9x² – x – 15 is divided by 2x + 3.
Solution:

Question 2.
Show that:
(i) x – 2 is a factor of 5x² + 15x – 50.
(ii) 3x + 2 is a factor of 3x² – x – 2.
(iii) x + 1 is a factor of x³ + 3x² + 3x + 1.
Solution:

Question 3.
Use the Remainder Theorem to find which of the following is a factor of 2x³ + 3x² – 5x – 6.
(i) x + 1
(ii) 2x – 1
(iii) x + 2
(iv) 3x – 2
(v) 2x – 3.
Solution:
(i) f(x) = 2×3 + 3×2 – 5x – 6

Question 4.
(i) If 2x + 1 is a factor of 2x² + ax – 3, find the value of a.
(ii) Find the value of k, if 3x – 4 is a factor of expression 3x² + 2x – k.
Solution:

Question 5.
Find the values of constants a and b when x – 2 and x + 3 both are the factors of expression, x³ + ax² + bx – 12.
Solution:

(x + 3) is a factor of f(x)
f(-3) = 0
9a – 3b – 39 – 0
⇒ 3a – b – 13 = 0
⇒ 3a – b = 13
Adding (i) and (ii) we get:
5a = 15 ⇒ a = 3
Substituting the value of a in (i)
2(3) + b = 2
⇒ 6 + b = 2
⇒ b = 2 – 6 = – 4
Hence a = 3, b = – 4

Question 6.
Find the value of k, if 2x + 1 is a factor of (3k + 2) x³ + (k – 1).
Solution:

Question 7.
Find the value of a, if x – 2 is a factor of 2x⁵ – 6x⁴ – 2ax³ + 6ax² + 4ax + 8.
Solution:

Question 8.
Find the values of m and n so that x – 1 and x + 2 both are factors of x³ + (3m + 1) x² + nx – 18.
Solution:

Question 9.
When x³ + 2x² – kx + 4 is divided by x – 2, the remainder is k. Find the value of constants.
Solution:
f(x) = x³ + 2x² – kx + 4

Question 10.
Find the value of a, if the division of ax³ + 9x² + 4x – 10 by x + 3 leaves a remainder 5.
Solution:

Question 11.
If x³ + ax² + bx + 6 has x – 2 as a factor and leaves a remainder 3 when divided by x – 3, find the values of a and b. [2005]
Solution:

Question 12.
The expression 2x³ + ax² + bx – 2 leaves remainder 7 and 0 when divided by 2x – 3 and x + 2 respectively. Calculate the values of a and b.
Solution:

Question 13.
What number should be added to 3x³ – 5x² + 6x so that when resulting polynomial is divided by x – 3, the remainder is 8 ?
Solution:

Question 14.
What number should be subtracted from x³ + 3x² – 8x + 14 so that on dividing it by x – 2, the remainder is 10.
Solution:

Question 15.
The polynomials 2x³ – 7x² + ax – 6 and x³ – 8x² + (2a + 1) x – 16 leave the same remainder when divided by x – 2. Find the value of ‘a’.
Solution:

Question 16.
If (x – 2) is a factor of the expression 7x³ + ax² + bx – 14 and when the expression is divided by (x – 3), it leaves a remainder 52, find the values of a and b.
Solution:

Question 17.
Find ‘a’ if the two polynomials ax³ + 3x² – 9 and 2x³ + 4x + a, leave the same remainder when divided by x + 3. (2015)
Solution:

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 8 Remainder and Factor Theorems Ex 8A are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.

Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion (Including Properties and Uses) Ex 7D

These Solutions are part of Selina Concise Mathematics Class 10 ICSE Solutions. Here we have given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion Ex 7D.

Other Exercises

• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion Ex 7A
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion Ex 7B
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion Ex 7C
• Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion Ex 7D

Question 1.
If a : b = 3 : 5, find : (10a + 3b) : (5a + 2b)
Solution:

Question 2.
If 5x + 6y : 8x + 5y = 8 : 9, find x : y
Solution:

Question 3.
If k (3x – 4y) : (2x – 3y) = (5x – 6y) : (4x – 5y), find x : y.
Solution:

Question 4.
Find the :
(i) duplicate ratio of 2√2 : 3√5
(ii) triplicate ratio of 2a : 3b,
(iii) sub-duplicate ratio of 9x² a⁴ : 25y⁶ b²
(iv) sub-triplicate ratio of 216 : 343
(v) reciprocal ratio of 3 : 5
(vi) ratio compounded of the duplicate ratio of 5 : 6, the reciprocal ratio of 25 : 42 and the sub-duplicate ratio of 36 : 49.
Solution:

Question 5.
Find the value of x, if :
(i) (2x + 3) : (5x – 38) is the duplicate ratio of √5 : √6
(ii) (2x + 1) : (3x + 13) is the sub-duplicate ratio of 9 : 25.
(iii) (3x -7): (4x + 3) is the sub-triplicate ratio of 8 : 27.
Solution:

Question 6.
What quantity must be added to each term of the ratio x : y so that it may become equal to c : d ?
Solution:

Question 7.
A woman reduces her weight in the ratio 7 : 5. What does her weight become if originally it was 84 kg?
Solution:
Ratio in reduction of weight = 7 : 5
Originally weight of the woman = 84 kg
Reduced weight = \(\frac { 84 x 5 }{ 7 }\) = 60 kg

Question 8.
If 15 (2x² – y²) = 7xy, find x : y, if x and y both are positive.
Solution:

Question 9.
Find the :
(i) fourth proportional to 2xy, x² and y².
(ii) third proportional to a² – b² and a + b.
(iii) mean proportion to (x – y) and (x³ – x²y)
Solution:
(i) Let a be the fourth proportional
Then 2xy : x² :: y² : a

Question 10.
Find two numbers such that the mean proportional between them is 14 and third proportional to them is 112.
Solution:
Let x and y be the two numbers.
Then 14 is the mean proportional between x and y
xy = 14² => xy = 196 ….(i)
and 112 is the third proportional to x, y
y² = 112 x ….(ii)

Question 11.
If x and y be unequal and x : y is the duplicate ratio of x + z and y + z, prove that z is mean proportional between x and y.
Solution:

Question 12.
If q is the mean proportional between p and r, prove that:

Solution:

Question 13.
If a, b and c are in continued proportion, prove that: a : c = (a² + b²) : (b² + c²).
Solution:

Question 14.

Solution:

Question 15.
If (4a + 9b) (4c – 9d) = (4a – 9b) (4c + 9d), prove that a : b = c : d.
Solution:

Question 16.

Solution:

Question 17.

Solution:

Question 18.
There are 36 members in a student council in a school and the ratio of the number of boys to the number of girls is 3 : 1. How many more girls should be added to the council so that the ratio of number of boys to the number of girls may be 9 : 5 ?
Solution:
Total number of members = 36
Ratio in boys and girls = 3 : 1

Question 19.
If 7x – 15y = 4x + y, find the value of x : y. Hence, use componendo and dividendo to find the values of:

Solution:

Question 20.

Solution:

Question 21.
If x, y, z arc in continued proportion, prove that

Solution:

Question 22.

Solution:

Question 23.

Solution:

Question 24.
Using componendo and dividendo, find the value

Solution:

Question 25.

Solution:

Question 26.

Solution:

Question 27.

Solution:

Hope given Selina Concise Mathematics Class 10 ICSE Solutions Chapter 7 Ratio and Proportion Ex 7D are helpful to complete your math homework.

If you have any doubts, please comment below. Learn Insta try to provide online math tutoring for you.